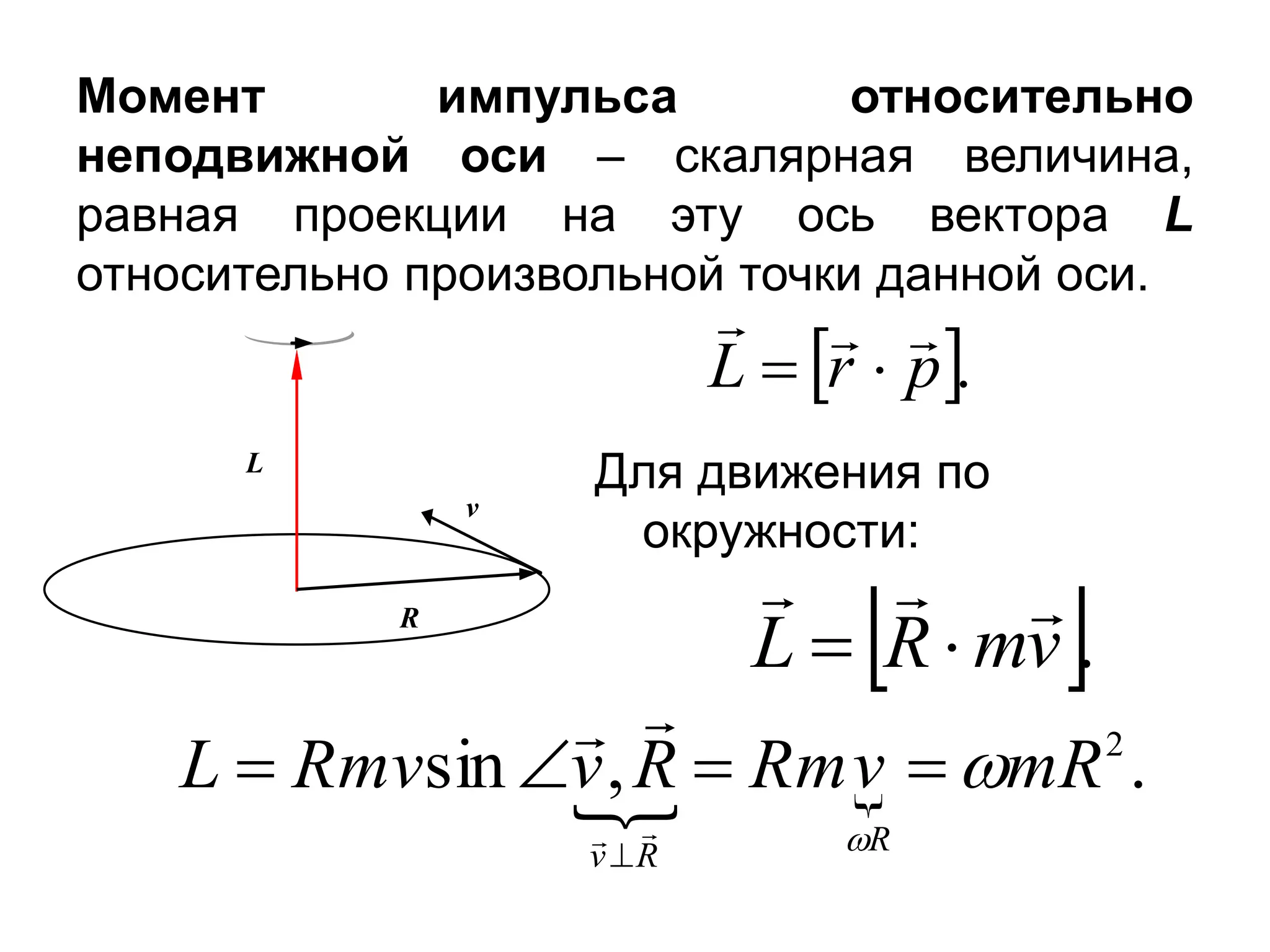
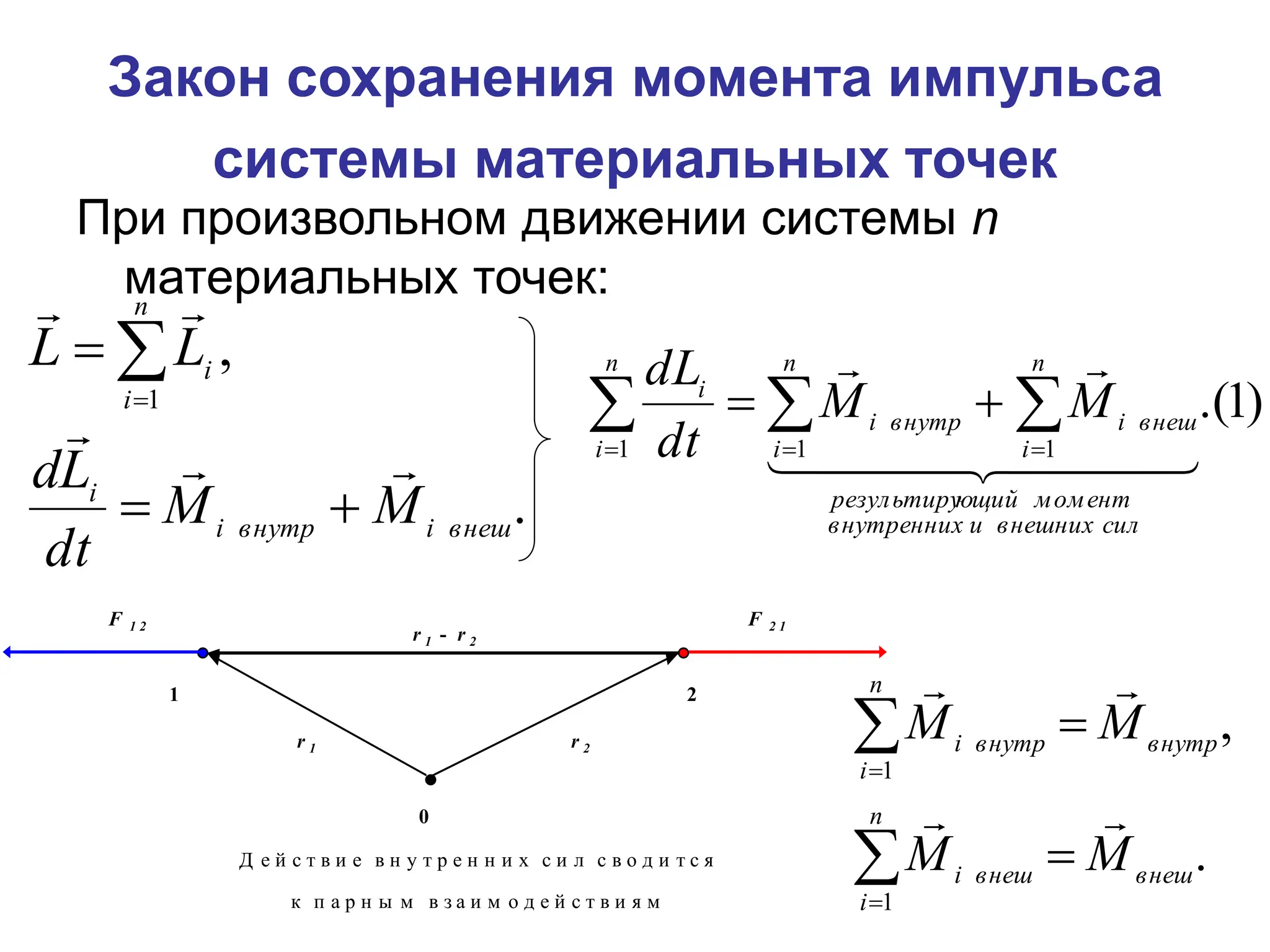
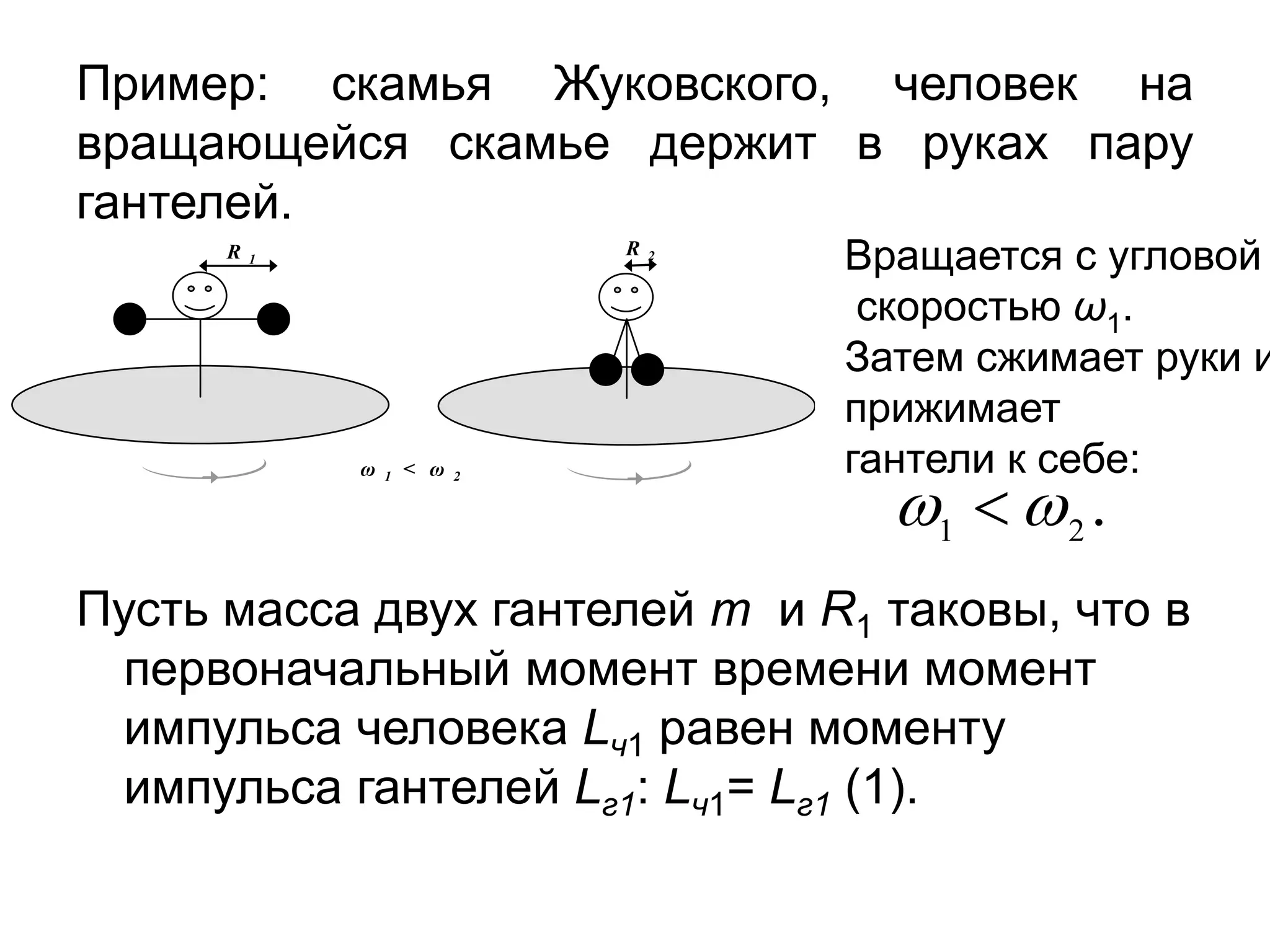
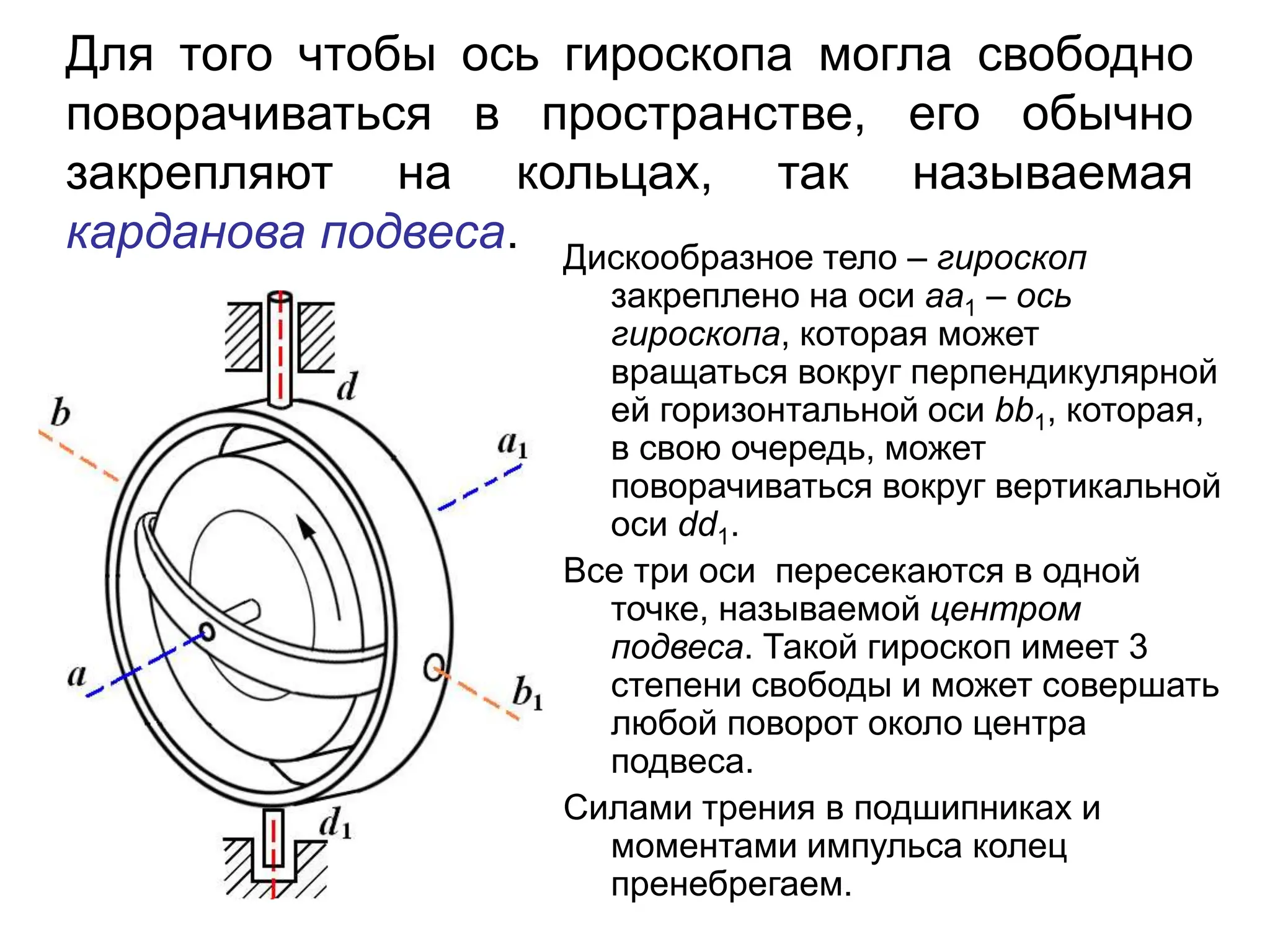
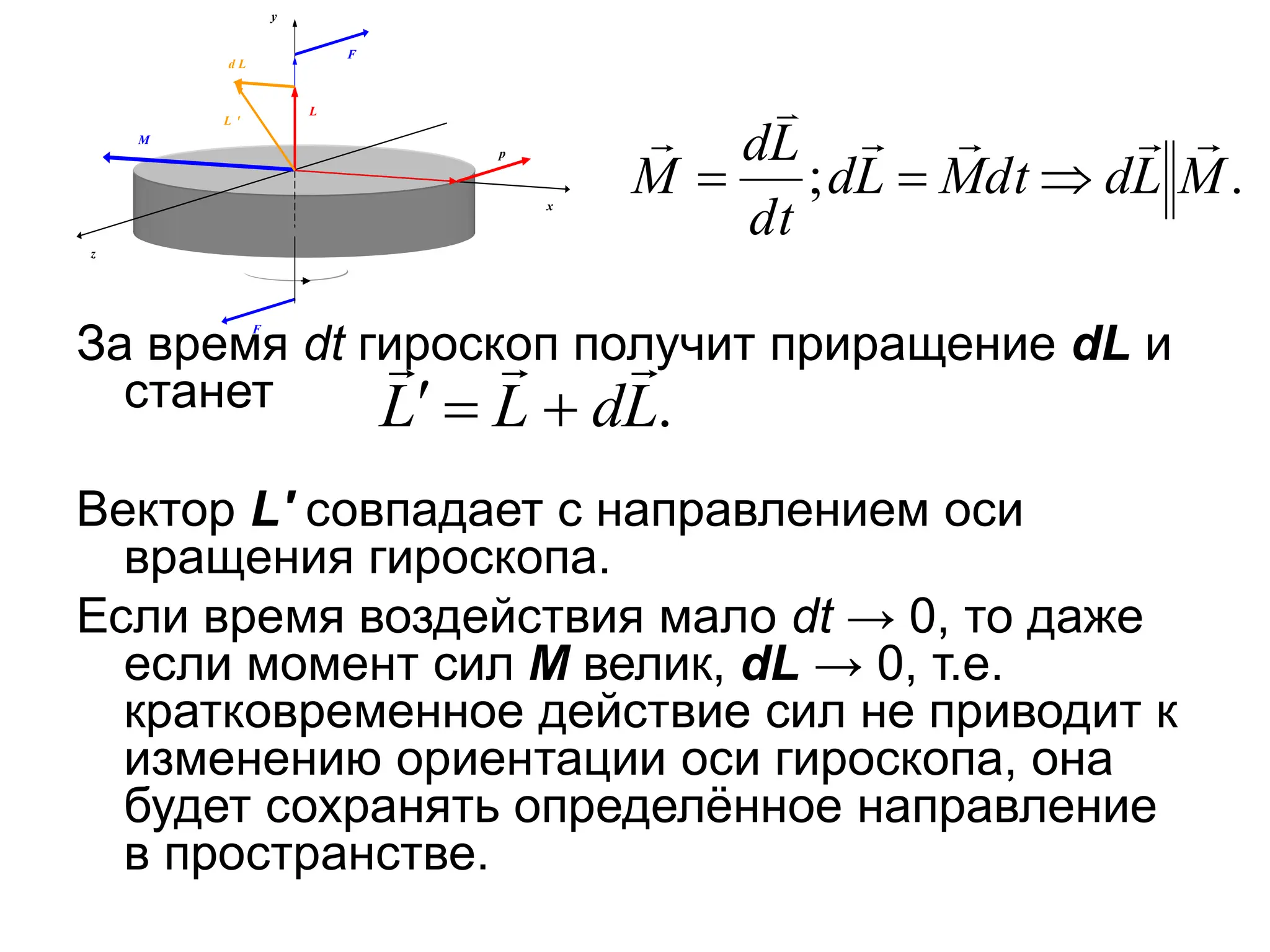
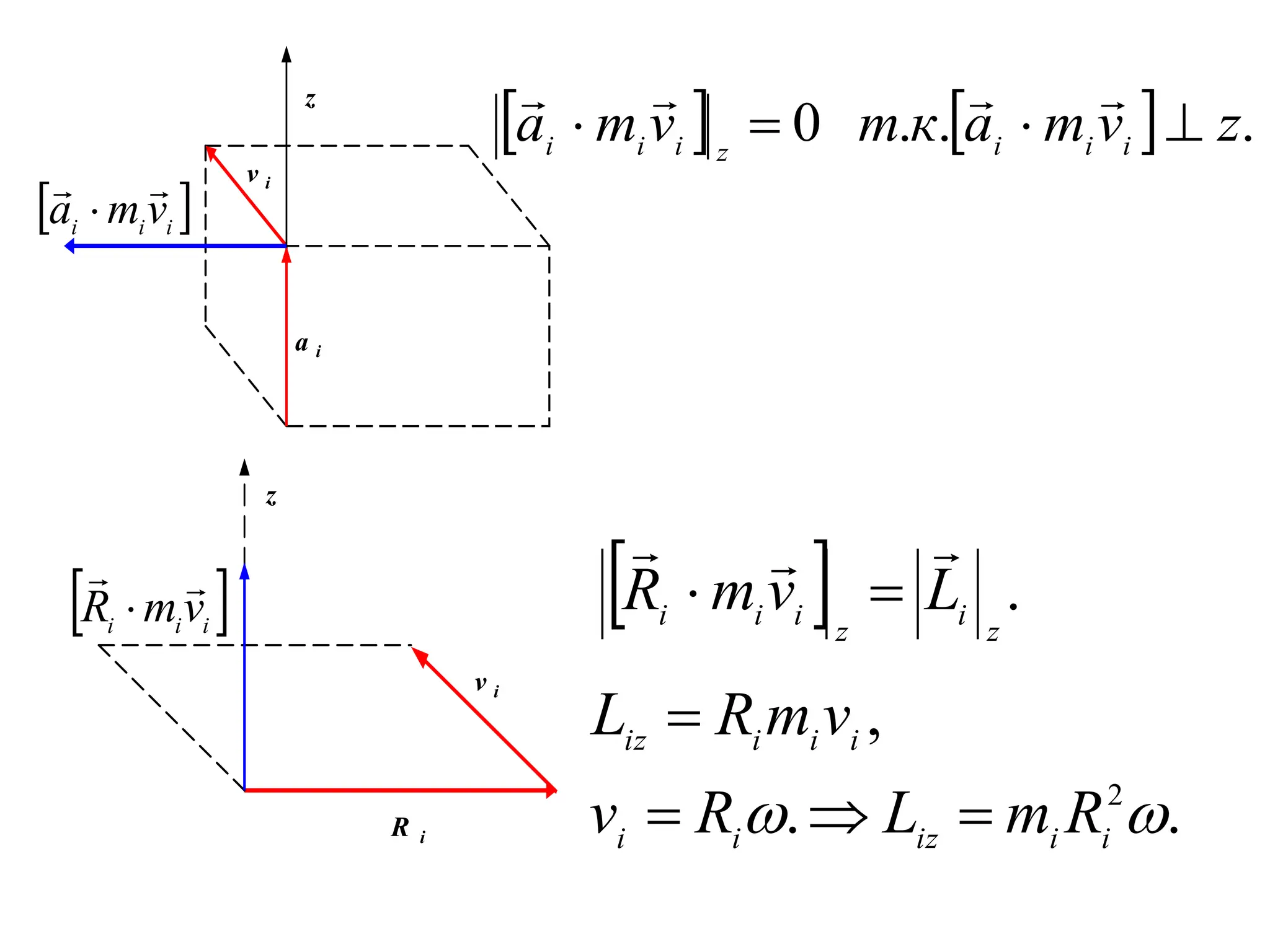
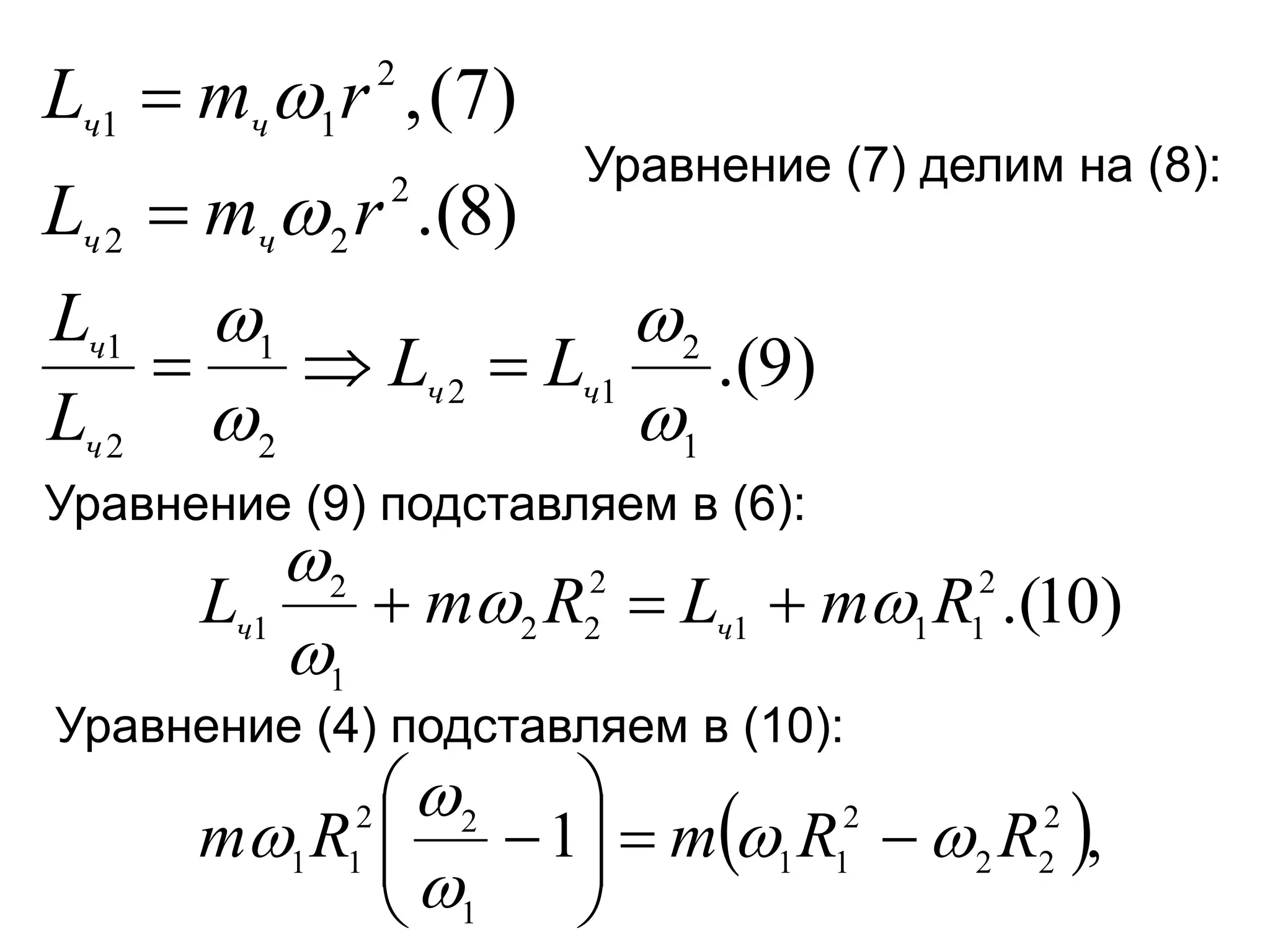Документ описывает закон сохранения момента импульса, который применим к системам материальных точек, и основывается на принципе статического равновесия твердых тел. Условия равновесия требуют, чтобы векторные суммы всех сил и моментов были равны нулю. Также рассматриваются свойства гироскопов и их приложения, подчеркивая их значимость в навигации и технике.

1. Закон сохранения момента
импульса системы
материальных точек
Момент силы и импульса
относительно точки и оси

2. Статика – инженерная наука, изучающая
равновесие твердых тел, находящихся под
действием сил. Она необходима для
определения максимально допустимых
нагрузок.
• Чтобы удержать тело в покое (равновесии),
необходимо выполнение 2-х условий:
1. Векторная сумма всех сил равна 0
2. Векторная сумма всех моментов сил равна 0
  0
i
F

  0
i
М


3. Момент силы F относительно неподвижной
точки 0 – физическая величина, определяемая
векторным произведением радиус-вектора r,
проведенного из точки 0 в точку приложения
силы, на силу F.
0
r
l
F
M
α
r
 
.
,
ор
псевдовект
M
F
r
M







.
sin
,
sin
силы
плечо
l
r
F
r
M











,
k
M
j
M
i
M
M z
y
x







      .
,
,
z
z
y
y
x
x
F
r
M
F
r
M
F
r
M













4. Момент силы
относительно
неподвижной оси –
скалярная величина,
равная проекции на
эту ось вектора М
относительно
произвольной точки
данной оси.
Значение Мz не зависит
от выбора положения
точки 0 на оси z.
0
r
F
M
M z
z

5. Момент импульса (количества движения)
материальной точки относительно неподвижной
точки 0 – физическая величина, определяемая
векторным произведением
0
r
l
p
L
α
r
   .
v
m
r
p
r
L









.
sin
,
sin
импульса
плечо
l
r
p
r
L











,
k
L
j
L
i
L
L z
y
x







      .
,
, z
z
y
y
x
x
p
r
L
p
r
L
p
r
L













6. Момент импульса относительно
неподвижной оси – скалярная величина,
равная проекции на эту ось вектора L
относительно произвольной точки данной оси.
Для движения по
окружности:
L
v
R
 .
p
r
L





 .
v
m
R
L





  .
,
sin 2
mR
v
Rm
R
v
Rmv
L
R
R
v












7. Уравнение моментов
Математическая справка:
.
M
dt
L
d 


  .
dt
dy
x
y
dt
dx
y
x
dt
d



 
 
    .
0
,
sin
,
0
M
dt
L
d
F
r
p
v
dt
L
d
dt
p
d
r
p
dt
r
d
p
r
dt
d
M
p
v
p
v
F
v
L
































































M
L





8. Производная по времени от
момента импульса относительно
точки равна моменту силы
относительно этой точки.
Производная по времени от момента
импульса относительно оси равна
моменту силы относительно этой оси.
.
M
dt
L
d 


.
,
, z
z
y
y
x
x
M
dt
dL
M
dt
dL
M
dt
dL




9. Закон сохранения момента импульса
системы материальных точек
При произвольном движении системы n
материальных точек:
.
,
1
внеш
i
внутр
i
i
n
i
i
M
M
dt
L
d
L
L







 
 )
1
.(
1
1
1


 


 



сил
внешних
и
внутренних
момент
ющий
результиру
n
i
внеш
i
n
i
внутр
i
n
i
i
M
M
dt
dL


 




r 2
r 1
r 1 - r 2
0
2
1
F 2 1
F 1 2
Д е й с т в и е в н у т р е н н и х с и л с в о д и т с я
к п а р н ы м в з а и м о д е й с т в и я м
.
,
1
1
внеш
n
i
внеш
i
внутр
n
i
внутр
i
M
M
M
M











10. Результирующий момент внутренних сил
в соответствии с третьим законом
Ньютона равен нулю.
 


 12
2
2 F
r
M



 
   
.
0
,
,
.
.
,
0
12
12
12
12
2
1
2
1













F
r
F
r
к
т
F
r
F
r
r
M
M











   
.
:
.
3
,
,
21
12
21
2
2
12
1
1
F
F
Ньютона
н
з
F
r
M
F
r
M
















11. В уравнении (1) операции
дифференцирования и суммирования
можно поменять местами:
Если внешние силы на систему не действуют,
то
Момент импульса замкнутой системы величина
постоянная, т.е. с течением времени не
меняется – закон сохранения момента
импульса.
)
1
.(
1
1
1


 


 



сил
внешних
и
внутренних
момент
ющий
результиру
n
i
внеш
i
n
i
внутр
i
n
i
i
M
M
dt
dL


 




.
1
внеш
n
i
i M
dt
L
d
L
dt
d 






.
0
0 const
L
dt
L
d
Мвнеш









12. Закон сохранения момента импульса
является прямым следствием законов
Ньютона и изотропности пространства –
эквивалентности свойств пространства
в различных направлениях.
Во многих задачах, связанных с
вращающимися системами, угловая
скорость вращения ω и момент
импульса можно вычислить с помощью
закона сохранения момента импульса.

13. Пример: скамья Жуковского, человек на
вращающейся скамье держит в руках пару
гантелей.
Пусть масса двух гантелей m и R1 таковы, что в
первоначальный момент времени момент
импульса человека Lч1 равен моменту
импульса гантелей Lг1: Lч1= Lг1 (1).
ω 1 < ω 2
R 1
R 2
Вращается с угловой
скоростью ω1.
Затем сжимает руки и
прижимает
гантели к себе:
.
2
1 
 

14.   )
2
.(
2
1
1
1
1
1
1
1
1 R
m
R
m
R
mv
R
Lг 
 


)
3
.(
2
1
1
1
1 R
m
L
L ч 

 )
4
.(
2
1
1
1 R
m
Lч 

)
5
.(
2
2
2
2
2 R
m
L
L ч 


Начальный момент импульса системы:
Во втором случае:
Т.к. Lч1= Lг1
По закону сохранения момента импульса
(уравнение (3) равно (5)):
)
6
.(
2
1
1
1
2
2
2
2 R
m
L
R
m
L ч
ч 
 



15. )
8
.(
)
7
(
,
2
2
2
2
1
1
r
m
L
r
m
L
ч
ч
ч
ч




)
9
.(
1
2
1
2
2
1
2
1




ч
ч
ч
ч
L
L
L
L



Уравнение (7) делим на (8):
Уравнение (9) подставляем в (6):
)
10
.(
2
1
1
1
2
2
2
1
2
1 R
m
L
R
m
L ч
ч 






Уравнение (4) подставляем в (10):
 ,
1 2
2
2
2
1
1
1
2
2
1
1 R
R
m
R
m 



 











16.  ,
1 2
2
2
2
1
1
1
2
2
1
1 R
R
m
R
m 



 










 
 
.
2
;
2
,
2
,
1
2
1
2
2
2
2
1
2
1
1
2
2
1
1
2
2
2
1
2
2
2
2
2
1
1
2
1
1
2
1
2




















R
R
R
R
R
R
R
R
R
R
R
R
Аналогичная ситуация возникает,
когда фигурист прижимает руки к себе
и начинает вращаться быстрее.

17. Гироскоп
• Гироскоп – быстро вращающееся
симметричное твердое тело, ось
вращения которого может изменять
свое направление в пространстве.
Происходит от греческого
 
наблюдаю
кружусь
скоп
гиро

18. Свойства гироскопа проявляются у
вращающихся небесных тел, снаряда
(пули), роторов турбин, установленных на
судах, волчка, юлы.
На свойствах гироскопа основаны различные
приборы и устройства, применяемые в
технике.
Свойства гироскопа проявляются при
выполнении двух условий:
1. ось вращения гироскопа должна иметь
возможность изменять своё положение в
пространстве;
2. частота вращения гироскопа вокруг своей оси
должна быть много больше скорости
изменения направления оси в пространстве.

19. Для того чтобы ось гироскопа могла свободно
поворачиваться в пространстве, его обычно
закрепляют на кольцах, так называемая
карданова подвеса. Дискообразное тело – гироскоп
закреплено на оси аа1 – ось
гироскопа, которая может
вращаться вокруг перпендикулярной
ей горизонтальной оси bb1, которая,
в свою очередь, может
поворачиваться вокруг вертикальной
оси dd1.
Все три оси пересекаются в одной
точке, называемой центром
подвеса. Такой гироскоп имеет 3
степени свободы и может совершать
любой поворот около центра
подвеса.
Силами трения в подшипниках и
моментами импульса колец
пренебрегаем.

20. Пока гироскоп неподвижен, его можно
ориентировать в пространстве любым
образом.
Если гироскоп начинает вращаться с большой
угловой скоростью ω, то при отсутствии
внешних сил (Fвнеш =0) М = 0 и т.е. ось
гироскопа сохраняет свое положение в
пространстве.

21. Если к оси
гироскопа y
приложить пару
сил F, то
возникает
вращающий
момент М.
x
y
z
p
F
F
L
M
d L
L ′


 x
M
z
F
y
F



;
Ось гироскопа поворачивается вокруг оси z,
а не вокруг х, как это могло показаться.
Это гироскопический эффект.

22. За время dt гироскоп получит приращение dL и
станет
Вектор L′ совпадает с направлением оси
вращения гироскопа.
Если время воздействия мало dt → 0, то даже
если момент сил М велик, dL → 0, т.е.
кратковременное действие сил не приводит к
изменению ориентации оси гироскопа, она
будет сохранять определённое направление
в пространстве.
.
L
d
L
L






.
; M
L
d
dt
M
L
d
dt
L
d
M









x
y
z
p
F
F
L
M
d L
L ′

23. Гироскоп
Применение:
- навигационные устройства (гирокомпас,
гирогоризонт),
- поддержание заданного направления
движения (автопилот).
При конструировании судов и самолетов
необходимо учитывать гироскопические
силы, возникающие в подшипниках
массивных валов двигателей, роторов
турбин, гребных валов и т.п.

24. Динамика вращательного
движения абсолютно
твёрдого тела
относительно неподвижной
оси
Основное уравнение
динамики вращательного
движения

25. При вращении абсолютно твёрдого тела вокруг
неподвижной оси z каждая отдельная точка
движется по окружности постоянного радиуса Ri
с некоторой скоростью vi.
Моменты силы:
Закон сохранения момента
импульса:
R i
v i
F
z
ω





0
,
y
x
z
y
x
M
и
M
k
M
j
M
i
M
M




.
z
z
M
dt
dL


26. Момент импульса
относительно точки 0 для i
точки твёрдого тела:
Проекция на ось z
относительно точки 0:
R i
v i
z
ω
r i
a i
0
   
 .
i
i
i
i
i
i
i
i v
m
R
a
v
m
r
L











i
L

 
 
    .
z
i
i
i
z
i
i
i
z
i
i
i
i
z
i
v
m
R
v
m
a
v
m
R
a
L

















27. a i
v i
 
i
i
i v
m
a



z
    .
.
.
0 z
v
m
a
к
т
v
m
a i
i
i
z
i
i
i 







R i
 
i
i
i v
m
R



v i
z
  .
z
i
z
i
i
i L
v
m
R





.
.
,
2

 i
i
iz
i
i
i
i
i
iz
R
m
L
R
v
v
m
R
L





28. Твёрдое тело – система жёстко
связанных материальных точек.
Следовательно, для твёрдого тела:
- момент инерции
материальной точки относительно оси z.
- момент инерции твердого тела
относительно оси z.
- момент импульса (количества
движения) твердого тела
относительно оси z.
.
1
2
1
2
1


 





n
i
i
i
n
i
i
i
n
i
iz
z R
m
R
m
L
L 

2
i
i
i R
m
J 



n
i
i
i
z R
m
J
1
2



n
i
iz
z L
L
1

29. Закон сохранения момента импульса:
Т.к. координатную ось z приняли
произвольно, индекс можно опустить.
– основное уравнение динамики
вращательного движения.
.
z
z J
L 

.
z
z
M
dt
dL

  .
z
z
z
z
M
J
dt
d
J
dt
J
d



 




 J
M

30. В общем случае:
– ускорение вращения твердого тела
относительно неподвижной оси прямо
пропорционально моменту всех внешних сил
относительно этой оси и обратно
пропорционально моменту инерции твердого
тела относительно этой оси.
• Физический смысл:
Момент инерции относительно оси – мера
инерции твердого тела при вращательном
движении относительно оси.
J
M





31. Момент инерции.
Теорема Гюйгенса-Штейнера
Момент инерции системы тел –
физическая величина равная сумме
произведений mi на :
В случае непрерывного распределения
масс сумма сводится к интегралу:
2
i
r
 
 .
2
i
i
r
m
J
.
2
2

 

V
m
dV
r
dm
r
J 

32. Кольцо
Диск, цилиндр
Стержень
Шар
l
.
2
mR
J 
.
2
2
mR
J 
.
12
2
ml
J 
.
5
2 2
mR
J 

33. Теорема Гюйгенса-Штейнера: момент
инерции относительно произвольной оси
равен моменту инерции относительно
параллельной ей оси, проходящей через
центр масс J0, сложенному с
произведением массы тела на квадрат
расстояния между ними а2.
a
l .
3
1
2
12
2
2
2
2
0 ml
l
m
ml
ma
J
J 










.
2
0 ma
J
J 


34. Пример: расчет момента инерции сплошного
цилиндра радиуса R, высотой h.
Разобьем на полые
цилиндры r, r + dr, dr→0.
dm – масса всего полого
цилиндра.
h
R
r
d r
,
2
dm
r
dJ
r
dr 






dr
rh
dm
rhdr
dV



2
2

 dr
r
h
dJ 3
2 

 



 
 h
R
V
hR
dr
r
h
dJ
J
R
2
4
0
3
,
2
1
2 





35.  



 
 h
R
V
hR
dr
r
h
dJ
J
R
2
4
0
3
,
2
1
2 




h
R
r
d r
.
2
2
mR
J 

36. Закон сохранения момента импульса АТТ
относительно неподвижной оси
В общем виде
В замкнутой системе
Фундаментальный закон, связан с
симметрией пространства, его
изотропностью, т.е. физические законы
не зависят от выбора направления осей
системы координат.
.
M
dt
L
d 


.
0

М

.
,
0
const
L
dt
L
d




37. Скамья Жуковского.
ω 1 < ω 2
R 1
R 2
 
.
0
.
2
.
2
2
1
2
0
1
2
1
0








R
const
J
mR
J
const
J
L






38. Кинетическая энергия при
вращательном движении АТТ
Т.к. имеется АТТ, следовательно, для всех
mi ω = const.
.
2
2
2
2
2
1
2
1
2
2
2
1
2



J
R
m
R
m
v
m
Е
J
n
i
i
i
n
i
i
i
n
i
i
i
к 


 

 








39. Динамика вращательного движения.
Работа и мощность при вращательном
движении относительно неподвижной оси
Основное уравнение динамики
вращательного движения:
Закон сохранения момента импульса:
Кинетическая энергия при вращательном
движении:
)
1
.(
;
dt
d
J
M
J
M 







.
const
J
L 
 
)
2
.(
2
2

J
Ек 

40. Работа при вращательном движении идёт на
увеличение его кинетической энергии:
Из (1) следует
Уравнение (5) подставляем в (4):
)
3
.(
к
dE
dA 
)
4
.(
2
2



d
J
J
d
dA 







)
5
.(
Mdt
Jd 

)
7
.(
)
6
.( 

 



 M
A
Md
Mdt
dA

41. Мощность:
)
8
.(





 M
dt
d
M
dt
dA
N

42. Плоское движение твердого тела
Плоское движение – движение, при
котором все участки траектории любых
двух точек твёрдого тела лежат в
параллельных плоскостях.
Кинетическая энергия складывается из
энергии поступательного движения и
энергии вращения.
,
2
2
2
2

c
c
к
J
mv
Е 

vc – скорость центра масс,
Jc – момент инерции относительно оси,
проходящей через центр масс.

43. Поступательное движение Вращательное движение
m J
r
 

dt
r
d
v



v
m
p



dt
p
d
F



m
F
a



2
2
mv
Ек 
;
FS
A  Fv
N 
dt
d







J
L 
dt
L
d
M



J
M




2
2

J
Ек 
;

M
A 
M
N 