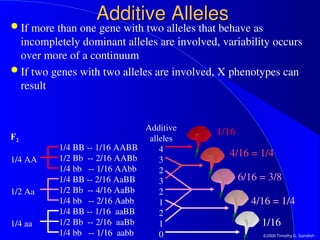
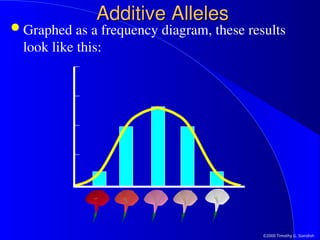
The document explores the concepts of quantitative genetics, emphasizing how traits are influenced by both genetic and environmental factors. It discusses the nature vs. nurture debate, the role of additive alleles, and methods to estimate genetic influences on traits, including heritability. Additionally, it presents statistics for describing variation in quantitative traits and implications for agricultural productivity.