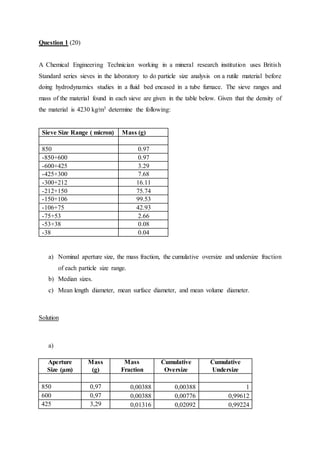
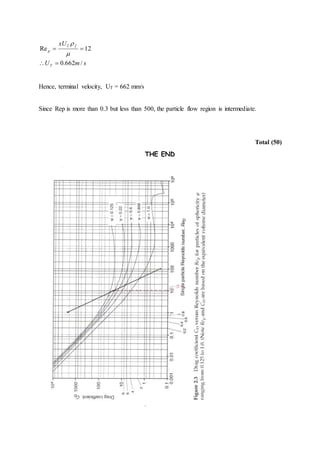
This document provides instructions for a chemical engineering assignment on particle size analysis. It includes 3 questions to be answered relating to sieve analysis data, calculating cumulative distribution from surface distribution, and estimating terminal velocity of a falling particle. Candidates must type their assignment, show all calculations, and include no more than 7 pages plus any appendices. It is due on September 1st at 4pm and is worth 50 total marks.

1. SUBJECT NAME: CHEMICAL PLANT IIIB
ASSIGNMENT (Memorandum): 26/08/2015
CODE: CMP33BT
DUE DATE: 01/09/2015
DUE TIME: 16:00
TOTAL MARKS: 50
FULL MARKS: 50
INSTRUCTIONS TO CANDIDATES:
 Assignment MUST be TYPED. No hand written assignment will be accepted.
 All calculations MUST be typed using the Microsoft Equation 3.0 function (on your
Microsoft Word document click “insert”, then “Object” and then click on “Microsoft
Equation 3.0”.
 No late assignments will be accepted.
 Do not copy the work of other candidates.
 Scan and attach all graphical calculations.
NUMBER OF PAGES (COVER PAGE INCLUDED): 7
NUMBER OF PAGES OF APPENDICES: 0
COURSE(S):
NATIONAL DIPLOMA: CHEMICAL
ENGINEERING
EXAMINER: MS. K. PREMLALL
MODERATOR: MR. L. KALOMBO

2. Question 1 (20)
A Chemical Engineering Technician working in a mineral research institution uses British
Standard series sieves in the laboratory to do particle size analysis on a rutile material before
doing hydrodynamics studies in a fluid bed encased in a tube furnace. The sieve ranges and
mass of the material found in each sieve are given in the table below. Given that the density of
the material is 4230 kg/m3 determine the following:
Sieve Size Range ( micron) Mass (g)
850 0.97
-850+600 0.97
-600+425 3.29
-425+300 7.68
-300+212 16.11
-212+150 75.74
-150+106 99.53
-106+75 42.93
-75+53 2.66
-53+38 0.08
-38 0.04
a) Nominal aperture size, the mass fraction, the cumulative oversize and undersize fraction
of each particle size range.
b) Median sizes.
c) Mean length diameter, mean surface diameter, and mean volume diameter.
Solution
a)
Aperture
Size (µm)
Mass
(g)
Mass
Fraction
Cumulative
Oversize
Cumulative
Undersize
850 0,97 0,00388 0,00388 1
600 0,97 0,00388 0,00776 0,99612
425 3,29 0,01316 0,02092 0,99224

3. 300 7,68 0,03072 0,05164 0,97908
212 16,11 0,06444 0,11608 0,94836
150 75,74 0,30296 0,41904 0,88392
106 99,53 0,39812 0,81716 0,58096
75 42,93 0,17172 0,98888 0,18284
53 2,66 0,01064 0,99952 0,01112
38 0,08 0,00032 0,99984 0,00048
0 0,04 0,00016 1 0,00016
250 1
b)
Median for Oversize = 150 µm
Median for Undersize = 100 µm

4. c)
Mean length diameter:
m
x
w
x
w
x
p
p
L 93
3
2



Mean surface diameter:
m
x
w
x
w
x
p
p
S 6.97
3



Mean volume diameter:
m
x
w
x
p
V 3.16
1
3
3



Question 2 (13)
Showing all steps, convert the surface distribution described by the following equation to
cumulative volume distribution:
mxxFs 75for)2cosh( 
mxFs 75for5 

5. Solution
)()( xFx
k
k
xF S
S
V
V  (1)
Integrating between sizes 0 and x
dxxfx
k
k
xF S
x
S
V
V )()(
0
  (2)
Noting that:
dx
dF
sf S
s )(
)2sinh(2
))2(cosh(
)( x
dx
xd
dx
dF
xf S
S  (3)
Substituting equation (3) into equation (2):
dxxx
k
k
xF
x
S
V
V )2sinh(2)(
0
 (4)
dxxx
k
k
xF
x
S
V
V 
0
)2sinh(2)(





 











 


4
)12()12(
8
)12()12(
2)(
22
0
22
xexe
k
kxexe
k
k
xF
xx
S
Vx
xx
S
V
V (5)
Constants
S
V
k
k
can be found by noting that FV(75) = 5
5
4
)1)75(2()1)75(2(
)75(
)75(2)75(2





 








ee
k
k
F
S
V
V
67
1063.9 

S
V
k
k
Therefore, for volume distribution,

6.   mxxexeF xx
V 75for)12()12(1041.2 2267
 
mxFV 75for5 
Question 3 (17)
A particle of equivalent volume diameter 300 µm, density 2000 kg/m3 and sphericity 0.22 falls
freely under gravity in air at 35 ºC and 1 atm. Estimate the terminal velocity reached by the
particle and determine the flow region of this particle.
Solution
For dry air at 20 ºC and 1 atm absolute pressure: 3
/145.1 mkgf  and sPa  6
1095.18
The first step is to calculate the dimensionless group 2
RepDC :
 
 
2251Re
)1095.18(
)81.9(145.12000)145.1()10300(
3
4
Re
3
4
Re
2
26
36
2
2
3
2








pD
pD
fpf
pD
C
C
gx
C


This is a relationship between drag coefficient CD and single particle Reynolds number Rep.
Since 2
RepDC is a constant, this relationship will give a straight line of slope -2 when plotted
on the log-log coordinates of the standard drag curve.
For plotting the relationship:
Rep CD
1 2251
10 22.51
100 0.2251
Where the plotted line intersects the standard drag curve for a sphericity of 0.22, Rep = 12.
The terminal velocity UT may be calculated from:

7. smU
xU
T
fT
p
/662.0
12Re




Hence, terminal velocity, UT = 662 mm/s
Since Rep is more than 0.3 but less than 500, the particle flow region is intermediate.
Total (50)
THE END