This document discusses parallel disk models and techniques for emulating a parallel disk head model on multiple disks that can each access one block per I/O. It presents several algorithms for writing and reading blocks in parallel across disks with low maximum load, including: 1) Queued writing that stores each block on two disks and achieves an expected write time of 1+exp(-D) for (1-ε)D blocks. 2) A majority method that stores each block on three disks and can schedule writes and reads together with maximum load O(log log n / log n). 3) Techniques for orienting allocation graphs to achieve maximum loads of 1, 2, and O(log log

1.
Parallel head disk emulation
Andy Twigg
Computer Lab

2.
Outline
● Outline
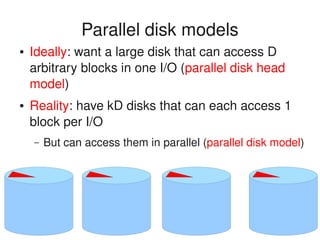
● Parallel disk models
● Emulations
● Open problems
● Bibliography
– [Sanders et al, soda00, spaa00, soda02] and
related work on balanced allocations [Czumaj,
Berenbrink,]

3.
Parallel disk models
● Ideally: want a large disk that can access D
arbitrary blocks in one I/O (parallel disk head
model)

4.
Parallel disk models
● Ideally: want a large disk that can access D
arbitrary blocks in one I/O (parallel disk head
model)
● Reality: have kD disks that can each access 1
block per I/O
– But can access them in parallel (parallel disk model)

5.
Parallel disk models
● Ideally: want a large disk that can access D
arbitrary blocks in one I/O (parallel disk head
model)
● Reality: have kD disks that can each access 1
block per I/O
– But can access them in parallel (parallel disk model)
● Can we emulate the parallel head model on pdm?
– Quality of emulation: throughput and delay of
requests, space overhead, ...

6.
Assumptions
● One global buffer of size m
– Shared among all disks
● Can access exactly one block
per disk per I/O (no rotational
latency, seeking, ...)
● Redundancy: each block will
be stored on two disks
– More generally, r out­of (r+1)

7.
Emulation: queued writing
● Assume pairwise­independent hash functions
f,g:[n]­>[n]. Consider D queues Q1
...QD
● Each block i will be stored at f(i),g(i)
● Write((1­)D blocks): append blocks to queues,
keep writing from queues until ∑i
|Qi
| < O(D/)

8.
Emulation: queued writing
● Assume pairwise­independent hash functions
f,g:[n]­>[n]. Consider D queues Q1
...QD
● Each block i will be stored at f(i),g(i)
● Write((1­)D blocks): append blocks to queues,
keep writing from queues until ∑i
|Qi
| < O(D/)
● Theorem [Sanders]:
– E[time to write (1­)D blocks] < 1+exp(­D)

9.
Aside: allocation processes
● Eg [Azar, Broder, Karlin, Upfal STOC94],
[Mitzenmacher 96], [Czumaj, Berenbrink, ..]
● m bins, n balls; ball i can go to 2 bins f(i),g(i)
chosen independently and uar
● Balls arrive online, thrown into least­loaded of
f(i),g(i)
● Interested in maxj
load(j)

10.
Allocation graphs and schedules
● Allocation graph GA
: nodes are disks(bins), edges
are blocks(balls). Undirected edge e={i,j} means
that block e stored on disks i,j.

11.
Allocation graphs and schedules
● Allocation graph GA
: nodes are disks(bins), edges
are blocks(balls). Undirected edge e={i,j} means
that block e stored on disks i,j.
● Schedule: given a set of requested edges S, GS
is
an orientation of GA
[S].

12.
Allocation graphs and schedules
● Allocation graph GA
: nodes are disks(bins), edges
are blocks(balls). Undirected edge e={i,j} means
that block e stored on disks i,j.
● Schedule: given a set of requested edges S, GS
is
an orientation of GA
[S].
● Load(disk j) = indegree(j) in GS
● #I/O steps = load(schedule) = maxj
indegree(j)
→ maintain online an orientation of low indegree
– If blocks stored at several disks, GA
is a hypergraph

13.
Warm up
● Fact: Every connected component of
G ~ G(D, (1/2­)D) is either a tree or a
tree with one cycle whp
● → Max load of a schedule with D/2
requests?

14.
Warm up
● Fact: Every connected component of
G ~ G(D, (1/2­)D) is either a tree or a
tree with one cycle whp
● → Max load of a schedule with D/2
requests?

15.
Warm up
● Orienting a tree:pick root, orient edges away from r
● Fact: Every connected component of
G ~ G(D, (1/2­)D) is either a tree or a
tree with one cycle whp

16.
Warm up
● Orienting a tree:pick root, orient edges away from r
● Orienting tree + cocycle of edge {u,v}: orient (v,u),
choose u as root and orient the remaining tree
● Fact: Every connected component of
G ~ G(D, (1/2­)D) is either a tree or a
tree with one cycle whp

17.
Warm up
● Orienting a tree:pick root, orient edges away from r
● Orienting tree + cocycle of edge {u,v}: orient (v,u),
choose u as root and orient the remaining tree
● Strategy: Divide requests into subsequences of
length D/2 and schedule each as above
– Max load 1 for each D/2 requests load 2N/D for N →
requests
● Fact: Every connected component of
G ~ G(D, (1/2­)D) is either a tree or a
tree with one cycle whp

18.
Max load 1.2*N/D
● Lemma[Pittel,Spencer,Wormald]: G ~ G(D,1.67D)
has no 3­core whp

19.
Max load 1.2*N/D
● Lemma[Pittel,Spencer,Wormald]: G ~ G(D,1.67D)
has no 3­core whp
● Strategy: Repeatedly pick the node with largest
remaining degree, orient edges toward it and
remove it
● max load 2 for each 1.67D requests

20.
Max load 1.2*N/D
● Lemma[Pittel,Spencer,Wormald]: G ~ G(D,1.67D)
has no 3­core whp
● Strategy: Repeatedly pick the node with largest
remaining degree, orient edges toward it and
remove it
● max load 2 for each 1.67D requests
● BUT: all these must buffer requests before
scheduling them

21.
Asynchronous reading:
Shortest­queue first
● Write(block i): buffer i, write i to both f(i),g(i) when
each becomes free
● Read(block i): buffer the request at the least­loaded
of f(i),g(i)
– each disk serves its queue in FIFO order

22.
Asynchronous reading:
Shortest­queue first
● Write(block i): buffer i, write i to both f(i),g(i) when
each becomes free
● Read(block i): buffer the request at the least­loaded
of f(i),g(i)
– each disk serves its queue in FIFO order
● Requests are scheduled online
● Conjecture[Sanders]: Delay O(log 1/) is achievable
for average arrival rate (1­)D
– If 2 copies of each block allowed (Theta(1/) for 1 copy)

23.
Max load O(log log n)
● Easier proof for lightly loaded case (n<d)
● Let G ~ G(n,n/8) and consider the following
while there exists a node of degree ≤ 13
for each such node
orient its edges towards it & remove
● Thm: max load = O(log log n)
– Claim 1: balls added at step i have height ≤ 13i
– Claim 2: largest connected component in G has size
O(log n)
– Claim 3: procedure terminates in O(log log n) steps

24.
Neat: majority method
● Use 3 (3­way ind) hash functions f,g,h
● Writing: Write block i to the least­loaded two of
f(i),g(i),h(i) along with a timestamp
● Reading: Read i from the least­loaded two of
f(i),g(i),h(i) and return the latest version
● Max load O(log log n / log n) for writing and
reading
● + writes and reads can be scheduled together

25.
Virtual disk model
● Want: A set of virtual disks V_1...V_m, each with
specified bandwidth b(V_i) and capacity c(V_i)
● Have: a collection of physical disks D_1...D_n,
each with bandwidth 1 and capacity c

26.
Virtual disk model
● Want: A set of virtual disks V_1...V_m, each with
specified bandwidth b(V_i) and capacity c(V_i)
● Have: a collection of physical disks D_1...D_n,
each with bandwidth 1 and capacity c
● Efficient emulation of virtual disk model?
– Admission control + (1­)­bandwidth emulation for
pdhm would imply ∑i
b(Vi
) < (1­)n and ∑i
c(Vi
) < cn/2
are sufficient conditions for vdm emulation
● Adding/removing virtual disks, changing
capacities, ...

27.
Extensions
Open:
● Prove good delay bounds for asynchronous
reading
● Deterministic guarantees (expanders?)
● Emulation of virtual disk model
● Handling rotational latencies, seek times