Download to read offline
Uploaded byEkansh Agarwal
Online File storage system using RSA and 3DES
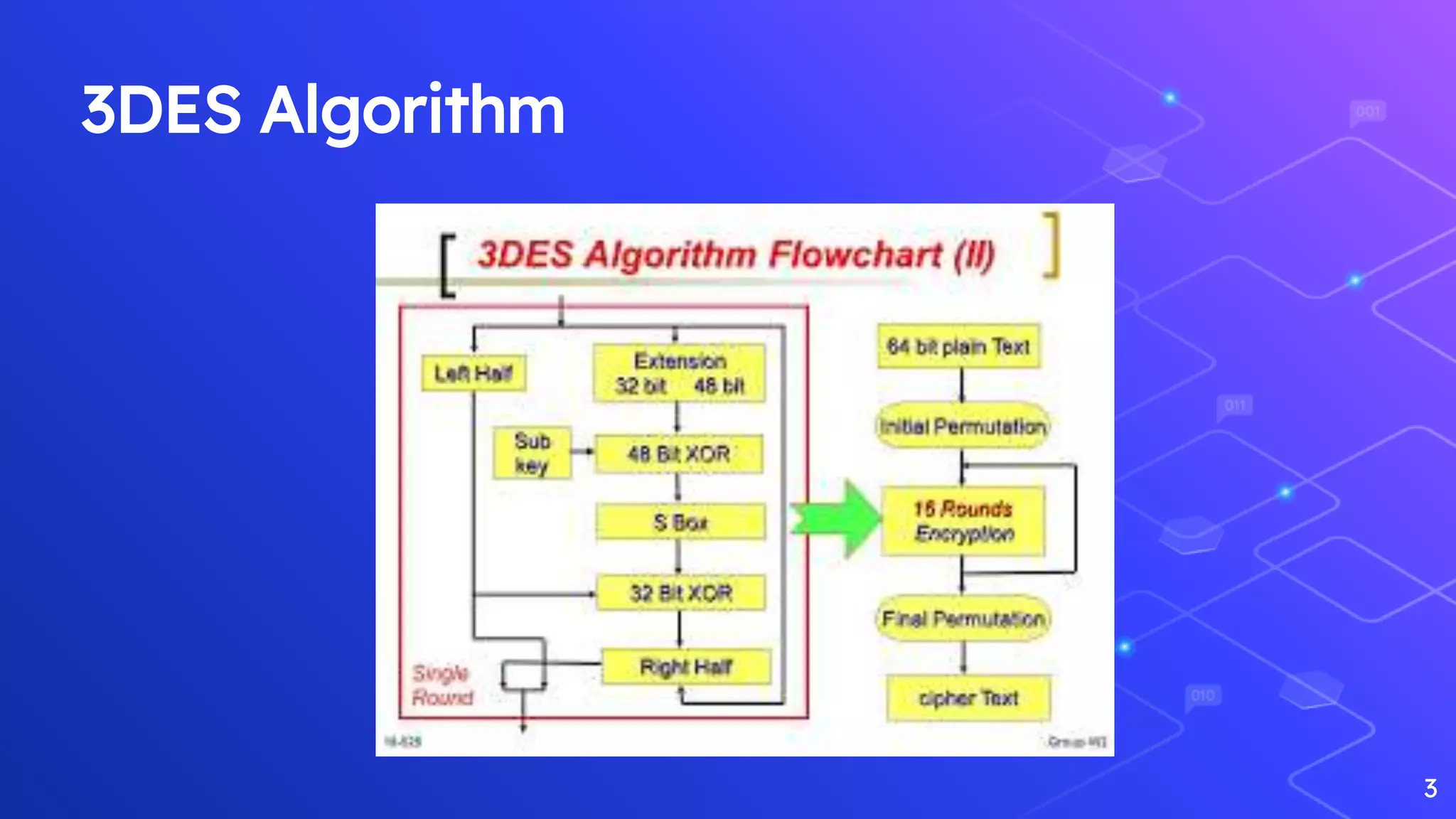
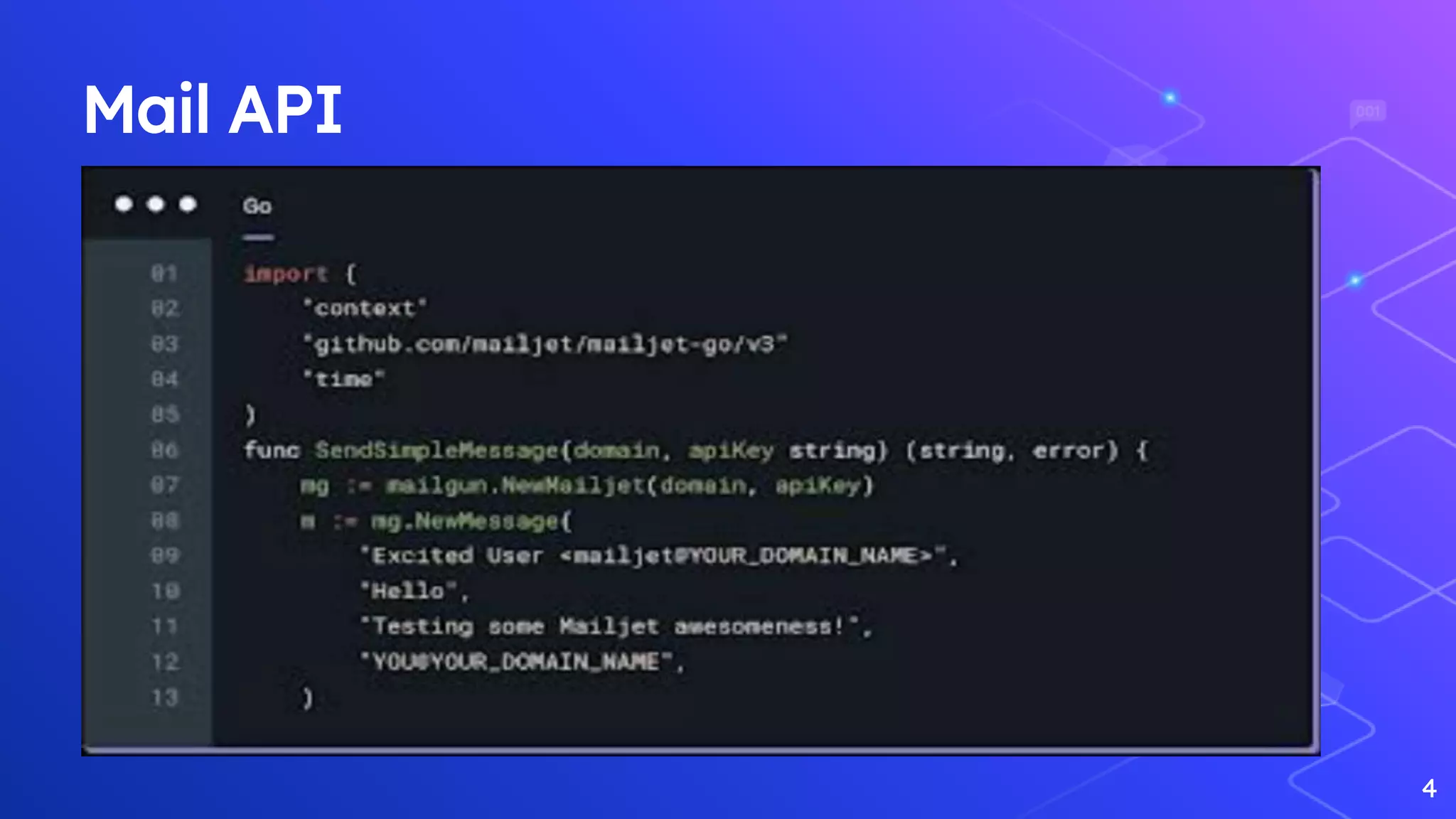
This document presents an online file storage system that uses RSA and 3DES encryption algorithms. It describes how files can be uploaded from a React client-side app to an Azure Storage blob using an Azure Storage SDK and shared access signature tokens. The document then references papers on RSA encryption and decryption as well as articles about Windows Azure storage services.
Online File storage system using RSA and 3DES
- 1. Online file storage system using RSAand 3DES By-: Ekansh Agarwal
- 2.
- 3.
- 4.
- 5. Implementation 5 Fig 1.3 EncryptionFig 1.4 decryption
- 6. Storage area Use an AzureStatic Web App (client-side React app) to upload a file to an Azure Storage blob using an Azure Storage npm package and an Azure Storage SAS token. 6
- 7. References • Zhou, Xin,and Xiaofei Tang. "Research and implementation of RSA algorithm for encryption and decryption." Proceedings of 2011 6th international forum on strategic technology. Vol. 2. IEEE, 2011. • Goshwe, Nentawe Y. "Data encryption and decryption using RSA algorithm in a network environment." International Journal of Computer Science and Network Security (IJCSNS) 13.7 (2013): 9. • Calder, Brad, et al. "Windows azure storage: a highly available cloud storage service with strong consistency." Proceedings of the Twenty-Third ACM Symposium on Operating Systems Principles. 2011. • Jennings, Roger. Cloud computing with the Windows Azure platform. John Wiley & Sons, 2010. 7
Editor's Notes
- #3 RSA algorithm uses the following procedure to generate public and private keys: Select two large prime numbers, p and q. Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption. If n = p x q, then the public key is <e, n>. RSA encrypts messages through the following algorithm, which is divided into 3 steps: Key Generation. I. Choose two distinct prime numbers p and q. II. Find n such that n = pq. ... Encryption. I. Person A transmits his/her public key (modulus n and exponent e) to Person B, keeping his/her private key secret. II. ... Decryption.
- #4 RSA algorithm uses the following procedure to generate public and private keys: Select two large prime numbers, p and q. Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption. If n = p x q, then the public key is <e, n>. RSA encrypts messages through the following algorithm, which is divided into 3 steps: Key Generation. I. Choose two distinct prime numbers p and q. II. Find n such that n = pq. ... Encryption. I. Person A transmits his/her public key (modulus n and exponent e) to Person B, keeping his/her private key secret. II. ... Decryption.
- #5 RSA algorithm uses the following procedure to generate public and private keys: Select two large prime numbers, p and q. Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption. If n = p x q, then the public key is <e, n>. RSA encrypts messages through the following algorithm, which is divided into 3 steps: Key Generation. I. Choose two distinct prime numbers p and q. II. Find n such that n = pq. ... Encryption. I. Person A transmits his/her public key (modulus n and exponent e) to Person B, keeping his/her private key secret. II. ... Decryption.
- #6 RSA algorithm uses the following procedure to generate public and private keys: Select two large prime numbers, p and q. Multiply these numbers to find n = p x q, where n is called the modulus for encryption and decryption. If n = p x q, then the public key is <e, n>. RSA encrypts messages through the following algorithm, which is divided into 3 steps: Key Generation. I. Choose two distinct prime numbers p and q. II. Find n such that n = pq. ... Encryption. I. Person A transmits his/her public key (modulus n and exponent e) to Person B, keeping his/her private key secret. II. ... Decryption.