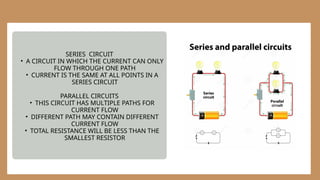
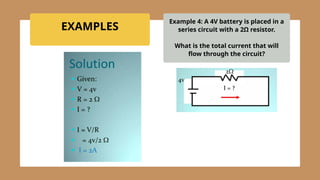
The document provides an overview of Ohm's Law, detailing its historical background, definitions of voltage, current, and resistance, and the implications of these concepts in direct current (DC) and alternating current (AC) circuits. It explains the relationships between these electrical properties through formulas, including the Ohm's Law triangle, and presents practical examples illustrating how to apply the law to various circuit scenarios. Furthermore, it differentiates between series and parallel circuits, explaining their characteristics and calculations involved.