The document discusses a study that found cooperating with others activates reward centers in the brain. Researchers used brain imaging to study women playing a game where they could choose cooperation or not. Surprisingly, the women experienced the most pleasure when both chose cooperation over acting selfishly. The longer they cooperated, the stronger the brain's reward response became. This suggests humans are wired to experience joy from cooperation with others.

1. "Why We're So Nice: We're Wired to Cooperate" Natalie Angier New York Times, 23 July 2002 What feels as good as chocolate on the tongue or money in the bank but won't make you fat or risk a subpoena from the Securities and Exchange Commission? Hard as it may be to believe in these days of infectious greed and sabers unsheathed, scientists have discovered that the small, brave act of cooperating with another person , of choosing trust over cynicism, generosity over selfishness, makes the brain light up with quiet joy . Studying neural activity in young women who were playing a classic laboratory game called the Prisoner's Dilemma , in which participants can select from a number of greedy or cooperative strategies as they pursue financial gain,researchers found that when the women chose mutualism over "me-ism," the mental circuitry normally associated with reward-seeking behavior swelled to life. And the longer the women engaged in a cooperative strategy, the more strongly flowed the blood to the pathways of pleasure. The researchers, performing their work at Emory University in Atlanta, used magnetic resonance imaging to take what might be called portraits of the brain on hugs. "The results were really surprising to us," said Dr. Gregory S. Berns, a psychiatrist and an author on the new report, which appears in the current issue of the journal Neuron. "We went in expecting the opposite." The researchers had thought that the biggest response would occur in cases where one person cooperated and the other defected, when the cooperator might feel that she was being treated unjustly. Also: Paul Glimcher invited talk on “Neuroeconomics” Wed@4

2. Internet Connectivity [Courtesy CAIDA]

3. International Trade [Krempel&Pleumper] A mixture of scales; detailed structure

4. Corporate Partnerships

5. Political and Governmental Control [Krempel]

6. Online Social Relationships [Isbell et al.]

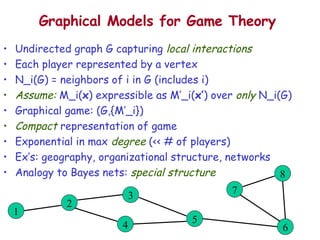
7. Multi-Player Game Theory: Powerpoint Notation Translation Players 1,…,n Actions (0 and 1 w.l.o.g.); joint action x in {0,1}^n Mixed strategy for i: probability p_i of playing 0 Payoff matrices M_i[ x ] for each i (size 2^n) (Approximate) Nash equilibrium: Joint mixed strategy p (product distribution) p_i is (approximate) best response to p for every player i Nash equilibria always exist; may be exponentially many Given the M_i, how can we compute/learn Nash equilibria? General problem is HARD.

8. Graphical Models for Game Theory Undirected graph G capturing local interactions Each player represented by a vertex N_i(G) = neighbors of i in G (includes i) Assume: M_i( x ) expressible as M’_i( x’ ) over only N_i(G) Graphical game: (G,{M’_i}) Compact representation of game Exponential in max degree (<< # of players) Ex’s: geography, organizational structure, networks Analogy to Bayes nets: special structure 2 4 3 5 8 7 6 1

9. An Abstract Tree Algorithm Downstream Pass: Each node V receives T(v,ui) from each Ui V computes T(w,v) and witness lists for each T(w,v) = 1 Upstream Pass: V receives values (w,v) from W s.t. T(w,v) = 1 V picks witness u for T(w,v), passes (v,ui) to Ui U1 U2 U3 W V T(w,v) = 1 <-->   an “upstream” Nash where V = v given W = w <-->  u : T(v,ui) = 1 for all i, and v is a best response to u ,w How to represent? How to compute?

10. An Approximation Algorithm Discretize u and v in T(v,u), 1 represents approximate Nash Main technical lemma: If k is max degree, grid resolution  ~  /(2^k) preserves global  -Nash equilibria An efficient algorithm: Polynomial in n and 2^k ~ size of rep. Represent an approx. to every Nash Can generate random Nash, or specific Nash U1 U2 U3 W V

11. Table dimensions are probability of playing 0 Black shows T(v,u) = 1 Ms want to match, Os to unmatch Relative value modulated by parent values   =  0.01,   = 0.05

12. Extension to exact algorithm: each table is a finite union of rectangles, exponential in depth Can also compute a single equilibrium exactly in polynomial time

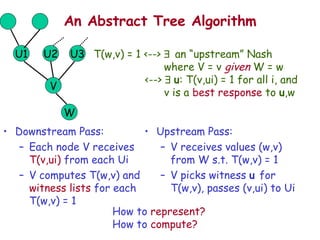
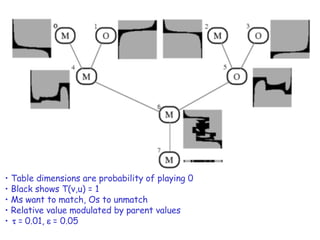
13. NashProp for Arbitrary Graphs Two-phase algorithm: Table-passing phase Assignment-passing phase Table-passing phase: Initialization: T[0](w,v) = 1 for all (w,v) Induction: T[r+1](w,v) = 1 iff  u : T[r](v,ui) = 1 for all i V=v a best response to W=w, U=u Table consistency stronger than best response U1 U2 U3 W V

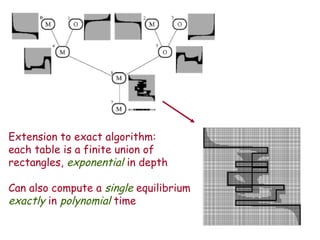
14. Convergence of Table-Passing Table-passing obeys contraction: {(w,v):T[r+1](w,v) = 1} contained in {(w,v):T[r](w,v) = 1} Tables converge and are balanced Discretization scheme: tables converge quickly Never eliminate an equilibrium Tables give a reduced search space Assignment-passing phase: Use graph to propagate a solution consistent with tables Backtracking local search Allow  and  to be parameters Alternative approach [Vickrey&Koller]: Constraint propagation on junction tree

17. Graphical Games: Related Work Koller and Milch: graphical influence diagrams La Mura: game networks Vickrey & Koller: other methods on graphical games

18. Summarization Games with Bounded Influence Have global summarization function S( x ) Payoff to player i depends only on x_i, S( x ): Arbitrary payoff function F_i(x_i,S( x )) Common examples: Voting (linear S) Financial markets Assume bounded influence of S Often expect influence   to decay with n! Assume bounded derivatives of the F_i Every player weakly influences every other

19. summarization value for any mixed strategy summarization value after best responses A Potential Function Argument

20. summarization value for any mixed strategy summarization value after best responses Learning Equilibria, Linear Summarization

21. Results Algorithm for computing O(  )-Nash in time polynomial in  Algorithm for learning O(  )-Nash in time polynomial in  , linear S case Benefits of a large population