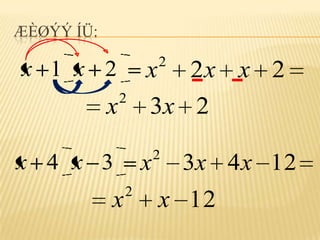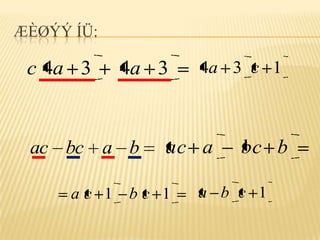2. 1. Ò¿âäýíãèéí Áîð ãýäýã ýìýãòýé ÿìàð õ¿í áàéñàí
1 áý?
2 2. Ìàíàé ñóðãóóëèéí Ìîíãîë õýëíèé áàãøèéí íýð.
3 3. Áèä ãî¸ áàéõûí òóëä þóíä õàðäàã âý?
4 4. Õàìãèéí óðò õîøóóòàé àìüòàí.
5 5. “ÇÀÕÍÀÀÒ” ¿ñãèéí áàéðûã ñîëüæ ¿ã á¿òýý.
6. ¯ðæ¿¿ëýõ áà çýðýãò äýâø¿¿ëýõ ¿éëäýë àãóóëñàí
6
àëãåáðûí èëýðõèéëýë.
7 7. Áàãøèéí ä¿í òàâüäàã äýâòýð.
8 8. Ìàíàé ñóðãóóëèéí àõìàä áàãøèéí íýð.

3. 1. Ò¿âäýíãèéí Áîð ãýäýã ýìýãòýé ÿìàð õ¿í áàéñàí
1 Á À À Ò À Ð áý?
2. Ìàíàé ñóðãóóëèéí Ìîíãîë õýëíèé áàãøèéí íýð.
2 Ñ À Ð À Í Ò Ó ß À
3 Ò Î Ë Ü 3. Áèä ãî¸ áàéõûí òóëä þóíä õàðäàã âý?
4 Ç À À Í 4. Õàìãèéí óðò õîøóóòàé àìüòàí.
5. “ÇÀÕÍÀÀÒ” ¿ñãèéí áàéðûã ñîëüæ ¿ã á¿òýý.
5 Õ À Í Ò À À Ç
6. ¯ðæ¿¿ëýõ áà çýðýãò äýâø¿¿ëýõ ¿éëäýë àãóóëñàí
6 Í Ý Ã Ã È Ø ¯ ¯ Í Ò àëãåáðûí èëýðõèéëýë.
7 Æ Ó Ð Í À Ë 7. Áàãøèéí ä¿í òàâüäàã äýâòýð.
8 Ë È Ì Á Ý Ý 8. Ìàíàé ñóðãóóëèéí àõìàä áàãøèéí íýð.

4. ÇÎÐÈËÃÎ:
Îëîí ãèø¿¿íòèéã îëîí ãèø¿¿íòýýð
¿ðæ¿¿ëýõ áîëîí îëîí ãèø¿¿íòèéã
á¿ëýãëýõ àðãààð ¿ðæèãäýõ¿¿íä
çàäëàõ ìýäëýãýý áàòàòãàõ
ã¿íçãèéð¿¿ëýõ.

5. ÇÎÐÈËÒ:
 Îëîí ãèø¿¿íòèéí òàëààðõ ìýäëýãýý ñýðãýýí ñàíàõ.
 Îëîí ãèø¿¿íòèéã îëîí ãèø¿¿íòýýð ¿ðæ¿¿ëýõ
ñòàíäàðò ä¿ðñòýé áè èõ àäâàðòàé áîëîõ.
 Îëîí ãèø¿¿íòèéã á¿ëýãëýõ àðãààð ¿ðæèãäýõ¿¿íä
çàäëàõ àäâàð ýçýìøèõ.
 Îëîí ãèø¿¿íò äýýðõ ¿éëäëèéã ã¿éöýòãýæ àñóóäëûã
øèéäâýðëýõ àäâàðòàé áîëîõ.

6. ÑÝÐÃÝÝÍ ÑÀÍÀÕ
Îëîí ãèø¿¿íòèéã îëîí
ãèø¿¿íòýýð ¿ðæ¿¿ëýõ

7. Íýã îëîí ãèø¿¿íòèéí ãèø¿¿í
òóñ á¿ðèéã íºãºº îëîí
ãèø¿¿íòèéí ãèø¿¿í òóñ
á¿ðýýð ¿ðæ¿¿ëíý.

8. ÆÈØÝÝ ÍÜ:
2
x 1 x 2 x 2x x 2
2
x 3x 2
2
x 4 x 3 x 3x 4 x 12
2
x x 12

9. ÎËÎÍ ÃÈØVVÍÒÈÉÃ ÁVËÝÃËÝÕ ÀÐÃÀÀÐ
VÐÆÈÃÄÝÕVVÍ ÁÎËÃÎÍ ÇÀÄËÀÕ
Íýìýõ ¿ðæèõ ¿éëäëèéí õóóëü
àøèãëàí îëîí ãèø¿¿íòèéí ãèø¿¿äèéã
òîõèðîìæòîéãîîð íü õààëòàíä
îðóóëàí áè èõèéã á¿ëýãëýõ àðãà
ãýíý.

10. ÆÈØÝÝ ÍÜ:
c 4a 3 4a 3 4a 3 c 1
ac bc a b ac a bc b
ac 1 bc 1 a b c 1

11. ªÌͪÃÎÂÜ ÀÉÌÃÈÉÍ 9-
Í ÃÀÉÕÀÌØÈÃÀÀÐ
ÀßËÖÃÀÀß

12. Áàÿí çàã
• (x+3)(2x+1)=
Ãóðâàí ñàéõàí óóë
• (x-2)(2x+3)=
Õîíãîðûí ýëñ
• (2m+4)(3m-9)=

13. Ãàëáûí ãîâü
• (x-3)(x-4)=
Õýðìýí öàâ
• 2a(x+y)+(x+y)=
Òîëü õàä
• 4x(a-b)-(a-b)=

14. Ñàíãèéí äàëàé õèéä
• x(a+b)+ay+by=
Àëãóé óëààí öàâ
• m(x+y)-xn-yn=
Ñýâðýé-̺íãºí ýäëýë
• 3a-3b+ax-bx=

15. ÃÝÐÈÉÍ ÄÀÀËÃÀÂÀÐ:
Ñóðàõ áè ãèéí
Õóóäàñ-
¹

16. ÀÍÕÀÀÐÀË
ÒÀÂÜÑÀÍ ØÀÂÜ
ÍÀÐÒÀÀ
ÁÀßÐËÀËÀÀ