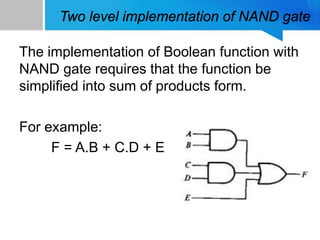
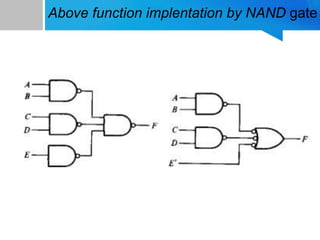
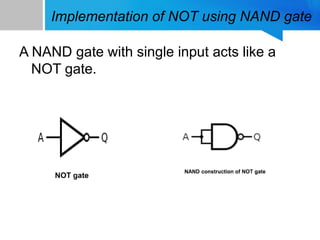
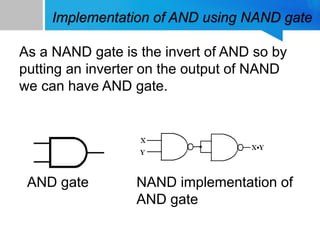
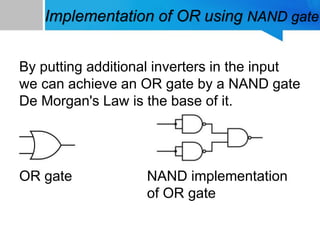
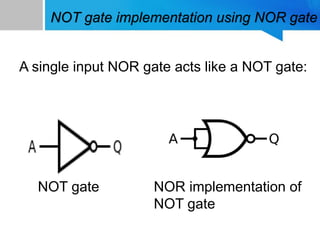
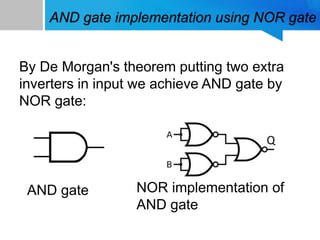
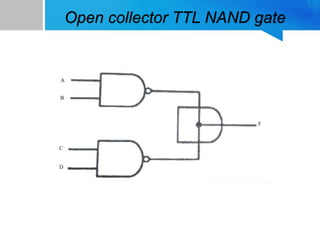
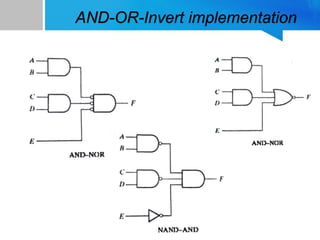
This presentation discusses the implementation of logic gates using NAND and NOR gates. It covers: 1) How to implement NOT, AND, and OR gates using only NAND gates by taking advantage of NAND gate properties and De Morgan's laws. 2) How to implement NOT, AND, and OR gates using only NOR gates in a similar manner. 3) Wired logic implementations using open collector NAND gates and ECL NOR gates. 4) The eight non-degenerate two-level logic forms and examples of AND-OR Invert and OR-AND Invert implementations.

2. Presentation submitted
By:
Muhammad Zubaid
Rasool
(MCSE-16-37)
 Muhammad Akhtar
(MCSE-16-10)
 Farhan Shaffi
(MCSE-16-31)
To:Sir. Imran

3. Our topics are
• NAND and NOR implementation
• Other two level implementation

4. We will discuss
• Basic logic gates implementation by
universal gates.
• Boolean function implementation by
universal gates.
• Wired Logic
• Non-degenerate forms

5. NAND and NOR implementation
In this topic we will discuss the following
things:
• Implementation of Basic gates using
Universal gate
• Implementation of Boolean functions
using Universal gates.

6. Universal Gates
• A gate that can be used to create any logic
gate is called universal gate. Hence NAND
and NOR are universal gates.
• Any Boolean function can be created
using AND OR and NOT gates.
• AND OR and NOT gates can be
implemented using NAND and NOR gates.

7. Implementation of NOT using NAND gate
A NAND gate with single input acts like a
NOT gate.

8. Implementation of AND using NAND gate
As a NAND gate is the invert of AND so by
putting an inverter on the output of NAND
we can have AND gate.
NAND implementation of
AND gate
AND gate

9. Implementation of OR using NAND gate
By putting additional inverters in the input
we can achieve an OR gate by a NAND gate
De Morgan's Law is the base of it.
OR gate NAND implementation
of OR gate

10. Symbolic equivalance of NAND gate
By De Morgan's Law we can describe NAND
gate graphically by the following symbols:

11. Two level implementation of NAND gate
The implementation of Boolean function with
NAND gate requires that the function be
simplified into sum of products form.
For example:
F = A.B + C.D + E

12. Above function implentation by NAND gate

13. NOT gate implementation using NOR gate
A single input NOR gate acts like a NOT gate:
NOT gate NOR implementation of
NOT gate

14. AND gate implementation using NOR gate
By De Morgan's theorem putting two extra
inverters in input we achieve AND gate by
NOR gate:
AND gate NOR implementation of
AND gate

15. OR gate implementation using NOR gate
As NOR is the invert of OR gate so by
putting an inverter in the output of NOR we
get OR gate:
OR gate NOR implementation of
OR gate

16. Graphical equivalance of NOR gate
By De Morgan's Law we can describe NOR
gate graphically by the following symbols:

17. Two level implementation of NOR gate
A two-level implementation with NOR gates
requires that the function be simplified
into product of sums form.
For example:
F = (AB' + A'B)(C + D')
Implementation using
NOR gate

18. Our 2nd Topic is
Other Two Level Implementation
We will discuss the following things in this
topic:
• Wired Logic.
• Non-degenerate Form

19. Other Two Level Implementations
• NAND and NOR gates are widely used in
the ICs.
• A few NAND or NOR gates allow the wire
connection between the outputs of two gates
for specific functionality.
• This wire connection is called the “wired
logic”.

20. Wired Logic gate
• A wired logic gate does not produce a
physical second level gate.
• It is a wire connection.
• For discussion we will assume the
following circuits as two level
implementation.

21. Open collector TTL NAND gate
• The most common example for AND wired logic
by NAND gate is open collector TTL NAND
gate.
• TTL stands for transistor-transistor logic.
• When open collector TTL NAND gate is tied
together it performs wired AND logic.
• AND gate is drawn with the lines going through
the center of the gate.

22. Open collector TTL NAND gate
• It means that wired AND gate is not a physical gate
but only a symbol to describe the functionality done
by the wired connection.
• The following logic implemented by circuit is called
AND-OR-Invert function.
F = (A.B)'...(C.D)' = (A.B+C.D)' = (A'+B').(C'+D')

23. Open collector TTL NAND gate

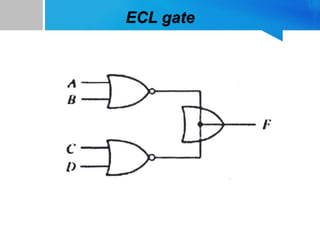
24. ECL gate
• ECL stands for Emitter Coupled Logic
• The NOR outputs of the ECL gate are tied
together to perform a wired-OR function.
• The following logic implemented by the circuit is
called OR-AND-Invert function.
F = (A+B)'+(C+D)' = [(A+B).(C+D)]'

25. ECL gate

26. Non-degenrate form
• There are 16 possible combinations of two
level forms.
• 8 of these are degenrate form because
they degenrate to a single operation.
• The remaining 8 are non-degenrate forms.

27. Non-degenrate form
• These forms are implemented in sum of products form or
product of sums form.
• The 8 nondegenrate forms are:
1.AND-OR 2.OR-AND
3.NAND-NAND 4.NOR-NOR
5.NOR-OR 6.NAND-AND
7.OR-NAND 8.AND-NOR
• The 1st gate listed in each of the forms
constitute first level while the 2nd gate
constitute the second level.

28. AND-OR-Invert implementation
• The two forms NAND-AND and AND-NOR
are equivalant.
• Both performs the AND-OR-Invert
function.
• AND-OR-Invert implementation requires
the expression in sum-of-products form.
• The following function is implemented:
F=(A.B+C.D+E)'

29. AND-OR-Invert implementation

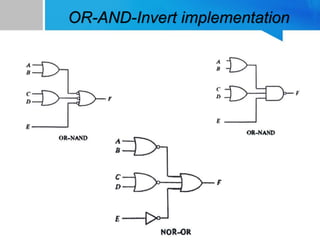
30. OR-AND-Invert implementation
• The OR-NAND and NOR-OR forms are
equivalant.
• Both performs OR-AND-Invert function.
• OR-AND-Invert implementation requires the
expression in product of sums form.
• The following function is implemented:
F=[(A+B).(C+D).E]'

31. OR-AND-Invert implementation