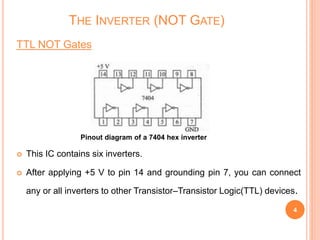
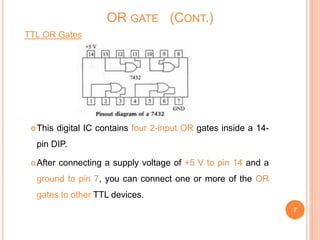
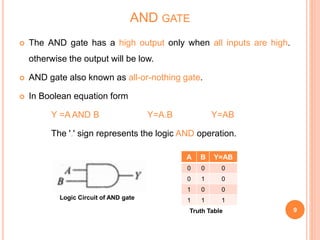
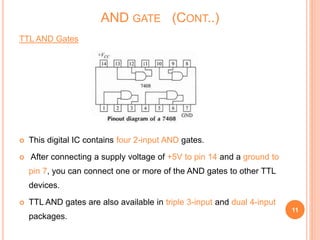
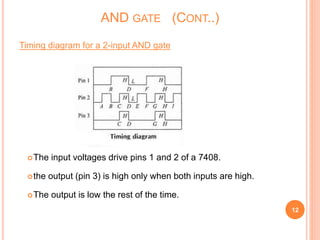
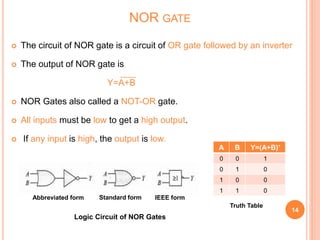
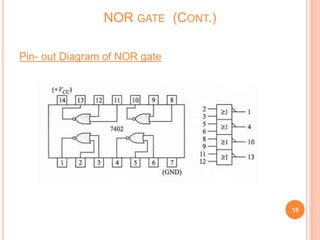
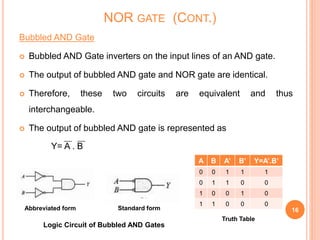
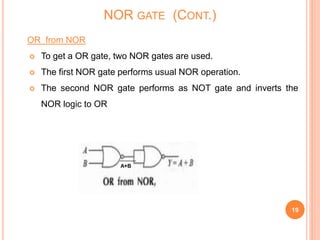
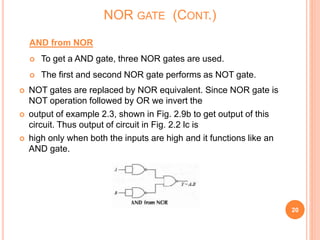
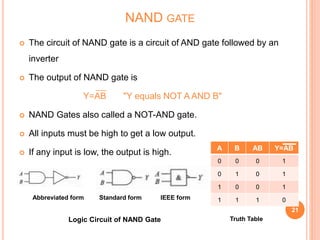
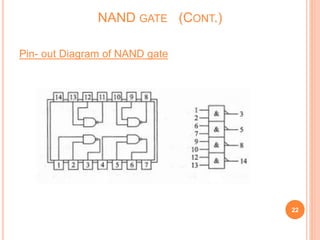
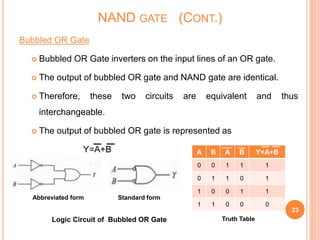
This document discusses digital logic gates. It begins by defining a gate as a digital circuit with one or more inputs and one output. The three basic gates are described as the NOT, OR, and AND gates. Additional universal gates, the NAND and NOR gates, are introduced. Truth tables are provided to explain the output of each gate for all possible input combinations. The document also discusses how to derive different gate functions using NAND and NOR gates alone through De Morgan's theorems.

1. DIGITAL LOGIC
 What is gate?
 The Basic Gates
 NOT gate
 OR gate
 AND gate
 Universal Logic Gates
 NOR gate
 NAND gate
1
Presented by,
M.Madhu Bala

2. GATES
 A digital circuit having one or more input signals but only one
output signal is called a gate.
 Connecting the basic gates in different ways makes it
possible to produce circuits.
 Gates are often called logic circuits.
 The basic gates can be used to produce any digital system.
 The three basic logic circuits are
 the inverter (NOT)
 the OR gate and
 the AND gate
2

3. THE INVERTER (NOT GATE)
 A NOT gate has one input signal and one output signal.
 The output Y of NOT gate is always complement of input A.
 In equation form
Y= NOT A Y=A‘ Y=A
 There are only two possible voltage levels (low and high) associated
with a digital circuit. This fits with the binary number system (0&1)
 This is often referred to as two-state operation.
 In the positive logic,
 the higher voltage level is assigned the binary value 1 (H=1)
 the lower voltage level is assigned the binary value 0 .(L=0)
3
A Y=A’
L H
H L
A Y=A’
0 1
1 0
Logic Circuit of NOT gate
Truth Table

4. THE INVERTER (NOT GATE)
TTL NOT Gates
Pinout diagram of a 7404 hex inverter
 This IC contains six inverters.
 After applying +5 V to pin 14 and grounding pin 7, you can connect
any or all inverters to other Transistor–Transistor Logic(TTL) devices.
4

5. OR GATE
 An OR gate has two or more input signals but only one output
signal.
 It is called an OR gate because the output voltage is high if any or
all of the input voltages are high.
 In Boolean equation form
Y = A OR B Y = A + B
The '+' sign represents the logic operation OR
 The number of rows in a truth table equals 2n, where n is the
number of inputs
5
Logic Circuit of OR gate
A B Y=A+B
0 0 0
0 1 1
1 0 1
1 1 1
Truth Table

6. Three- input OR gate
 The inputs are A, B, and C.
 When all inputs are low, the output is low.
 If any input is high, the output will be high.
 Boolean Equation Form:
Y = A+B+C
6
OR GATE (CONT..)
A B C Y=A+B+C
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1Logic Circuit of 3-input OR gate
Truth Table

7. TTL OR Gates
This digital IC contains four 2-input OR gates inside a 14-
pin DIP.
After connecting a supply voltage of +5 V to pin 14 and a
ground to pin 7, you can connect one or more of the OR
gates to other TTL devices.
7
OR GATE (CONT.)

8. Timing diagram for 2-input OR gate
 The input voltages drive pins 1 and 2 of a 7432.
 The output (pin 3) is low only when both inputs are low.
 The output is high the rest of the time.
8
OR GATE (CONT..)

9.  The AND gate has a high output only when all inputs are high.
otherwise the output will be low.
 AND gate also known as all-or-nothing gate.
 In Boolean equation form
Y =A AND B Y=A.B Y=AB
The '.' sign represents the logic AND operation.
9
AND GATE
A B Y=AB
0 0 0
0 1 0
1 0 0
1 1 1Logic Circuit of AND gate
Truth Table

10. Three- input AND gate
 The inputs are A, B, and C.
 When all inputs are high, the output is high.
 If even one input is low, the output is in the low state.
 In Boolean equation form:
Y=A.B.C Y=ABC
10
AND GATE (CONT..)
A B C Y=ABC
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Logic Circuit of AND gate
Truth Table

11. TTL AND Gates
 This digital IC contains four 2-input AND gates.
 After connecting a supply voltage of +5V to pin 14 and a ground to
pin 7, you can connect one or more of the AND gates to other TTL
devices.
 TTL AND gates are also available in triple 3-input and dual 4-input
packages.
11
AND GATE (CONT..)

12. Timing diagram for a 2-input AND gate
The input voltages drive pins 1 and 2 of a 7408.
the output (pin 3) is high only when both inputs are high.
The output is low the rest of the time.
12
AND GATE (CONT..)

13. The NAND & NOR gates are called universal gates because
they can perform all the logical operations of basis gates like
AND, OR, NOT.
13
Universal Logic Gate

14.  The circuit of NOR gate is a circuit of OR gate followed by an inverter
 The output of NOR gate is
Y=A+B
 NOR Gates also called a NOT-OR gate.
 All inputs must be low to get a high output.
 If any input is high, the output is low.
14
NOR GATE
Logic Circuit of NOR Gates
Abbreviated form Standard form IEEE form
Truth Table
A B Y=(A+B)’
0 0 1
0 1 0
1 0 0
1 1 0

15. Pin- out Diagram of NOR gate
15
NOR GATE (CONT.)

16. Bubbled AND Gate
 Bubbled AND Gate inverters on the input lines of an AND gate.
 The output of bubbled AND gate and NOR gate are identical.
 Therefore, these two circuits are equivalent and thus
interchangeable.
 The output of bubbled AND gate is represented as
Y= A . B
16
NOR GATE (CONT.)
Abbreviated form Standard form
Truth Table
A B A’ B’ Y=A’.B’
0 0 1 1 1
0 1 1 0 0
1 0 0 1 0
1 1 0 0 0
Logic Circuit of Bubbled AND Gates

17. De Morgan's First Theorem
NOR gate : Y=(A+B)’
bubbled AND gate : Y=A’B’
 The outputs are equal for the same inputs, so that (A+B)’ = A’B’
 The complement of a sum equals the product of the complements.
This identity is known as De Morgan’s, first theorem.
 This can also be proved by comparing the truth tables of NOR and
bubbled AND gates.
 Three input NOR gate and three input bubbled AND gate are
identical and it can write, (A+ B + C)' = A'B'C'
 This equivalence can be extended to gates or circuits for larger
number of inputs, too.
17
NOR GATE (CONT.)

18. NOT from NOR
 To get a NOT gate, tie inputs of NOR gate together so that there is
only one input to the circuit.
 If input is 0, then both the inputs to NOR gate are 0 that gives output
1.
 Similarly, if input is 1, both the inputs to NOR gate are 1 that gives
output 0.
 Therefore the output of circuit is complement of its input and thus
gives NOT operation.
18
NOR GATE (CONT.)

19. OR from NOR
 To get a OR gate, two NOR gates are used.
 The first NOR gate performs usual NOR operation.
 The second NOR gate performs as NOT gate and inverts the
NOR logic to OR
19
NOR GATE (CONT.)
A+B

20. AND from NOR
 To get a AND gate, three NOR gates are used.
 The first and second NOR gate performs as NOT gate.
 NOT gates are replaced by NOR equivalent. Since NOR gate is
NOT operation followed by OR we invert the
 output of example 2.3, shown in Fig. 2.9b to get output of this
circuit. Thus output of circuit in Fig. 2.2 lc is
 high only when both the inputs are high and it functions like an
AND gate.
20
NOR GATE (CONT.)

21.  The circuit of NAND gate is a circuit of AND gate followed by an
inverter
 The output of NAND gate is
Y=AB "Y equals NOT A AND B"
 NAND Gates also called a NOT-AND gate.
 All inputs must be high to get a low output.
 If any input is low, the output is high.
21
NAND GATE
Logic Circuit of NAND Gate
Abbreviated form Standard form IEEE form
Truth Table
A B AB Y=AB
0 0 0 1
0 1 0 1
1 0 0 1
1 1 1 0

22. Pin- out Diagram of NAND gate
22
NAND GATE (CONT.)

23. Bubbled OR Gate
 Bubbled OR Gate inverters on the input lines of an OR gate.
 The output of bubbled OR gate and NAND gate are identical.
 Therefore, these two circuits are equivalent and thus
interchangeable.
 The output of bubbled OR gate is represented as
Y=A+B
23
NAND GATE (CONT.)
A B A B Y=A+B
0 0 1 1 1
0 1 1 0 1
1 0 0 1 1
1 1 0 0 0
Abbreviated form Standard form
Truth TableLogic Circuit of Bubbled OR Gate

24. De Morgan's Second Theorem
NAND Gate :(AB)’
Bubbled OR Gate : Y=A’+B’
 The outputs are equal for the same inputs, so that (AB)’ = A’+B’
 The complement of a product equals the sum of the complements.
This identity is known as De Morgan’s second theorem.
 This can also be proved by comparing the truth tables of NAND gate
and bubbled OR gate.
 Three input NAND gate and three input bubbled OR gate are identical
and it can write, (ABC)' = A’+B‘+C’
 This equivalence can be extended to gates or circuits with any number
of inputs.
24
NAND GATE (CONT.)

25. THANK YOU
25