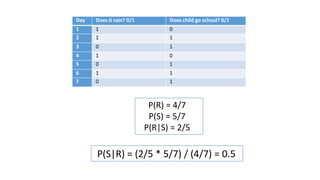
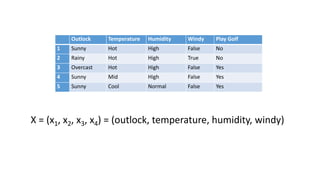
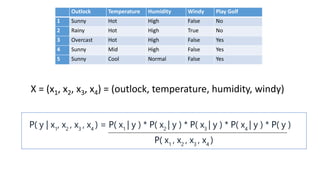
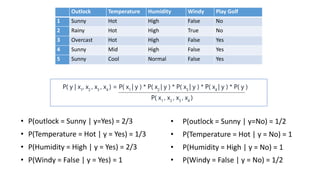
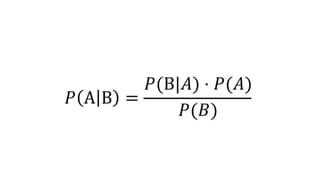The document discusses the Naive Bayes classifier and provides examples of its use. It begins by explaining the basic probabilities involved in a Naive Bayes model using a simple example of weather and whether a child goes to school. It then shows how to calculate the probabilities for a golf example using weather attributes. Finally, it demonstrates how to classify a new example and lists some common applications of Naive Bayes classifiers like text classification and recommendation systems.

1. Naive Bayes Classifier
By Tharuka Vishwajith

3. Day Does it rain? 0/1 Does child go school? 0/1
1 1 0
2 1 1
3 0 1
4 1 0
5 0 1
6 1 1
7 0 1
Probability of raining as P(R)
Probability of going to school as P(S)
When raining, probability of going to school is P(S|R)
When student is going to school, probability of raining is P(R|S)

4. P(R) = 4/7
P(S) = 5/7
P(R|S) = 2/5
Day Does it rain? 0/1 Does child go school? 0/1
1 1 0
2 1 1
3 0 1
4 1 0
5 0 1
6 1 1
7 0 1
P(S|R) = (2/5 * 5/7) / (4/7) = 0.5

5. X = (x1, x2, x3, x4) = (outlock, temperature, humidity, windy)
Outlock Temperature Humidity Windy Play Golf
1 Sunny Hot High False No
2 Rainy Hot High True No
3 Overcast Hot High False Yes
4 Sunny Mid High False Yes
5 Sunny Cool Normal False Yes

6. X = (x1, x2, x3, x4) = (outlock, temperature, humidity, windy)
Outlock Temperature Humidity Windy Play Golf
1 Sunny Hot High False No
2 Rainy Hot High True No
3 Overcast Hot High False Yes
4 Sunny Mid High False Yes
5 Sunny Cool Normal False Yes

7. Outlock Temperature Humidity Windy Play Golf
1 Sunny Hot High False No
2 Rainy Hot High True No
3 Overcast Hot High False Yes
4 Sunny Mid High False Yes
5 Sunny Cool Normal False Yes
• P(outlock = Sunny | y=Yes) = 2/3
• P(Temperature = Hot | y = Yes) = 1/3
• P(Humidity = High | y = Yes) = 2/3
• P(Windy = False | y = Yes) = 1
• P(outlock = Sunny | y=No) = 1/2
• P(Temperature = Hot | y = No) = 1
• P(Humidity = High | y = No) = 1
• P(Windy = False | y = No) = 1/2

8. We have given a day with Sunny, Hot, High humidity and
no wind.
Is it good day to play golf?
P(y=Yes|X) ∝ 2/3 * 1/3 * 1/3 * 1 = 0.07
P(y=No|X) ∝ 1/2 * 1 * 1 * 1/2 = 0.25
P(y=Yes|X) < P(y=No|X), So the day is not good for play golf.

9. Applications of Naive Bayes Algorithms
• Real time Prediction
• Multi class Prediction:
• Text classification/ Spam Filtering/ Sentiment Analysis
• Recommendation System