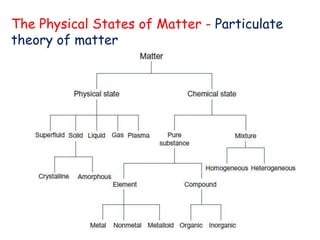
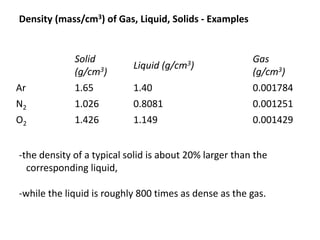
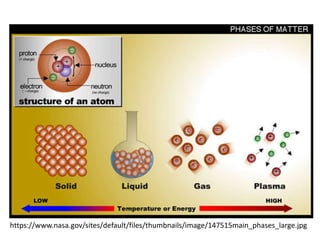
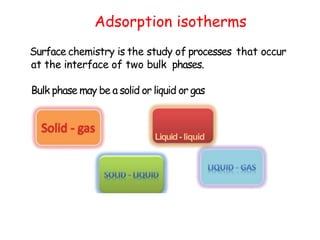
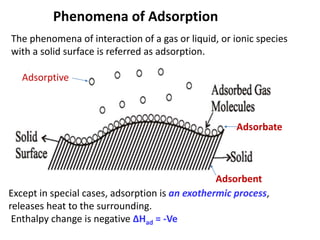
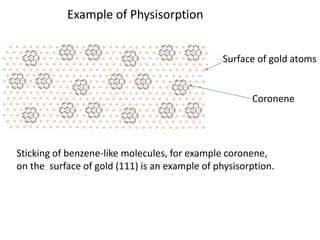
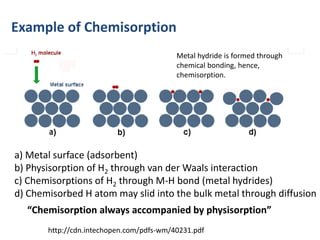
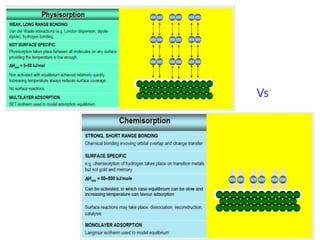
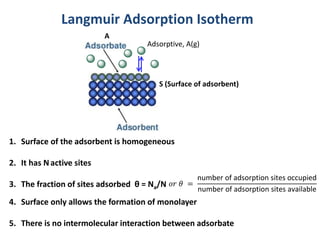
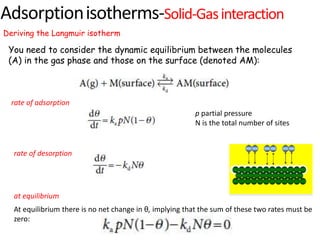
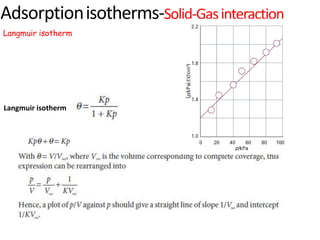
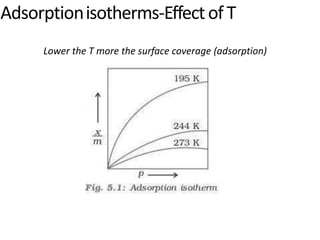
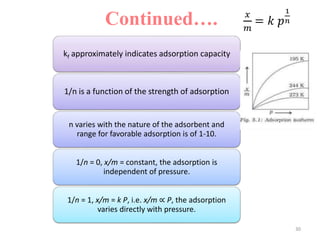
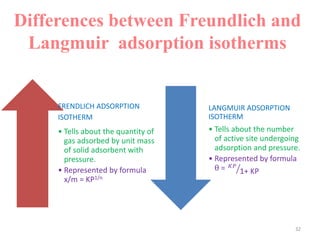
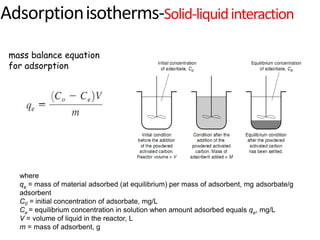
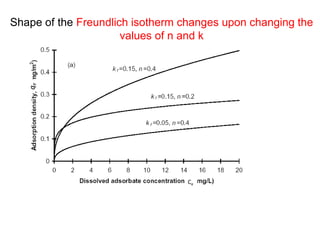
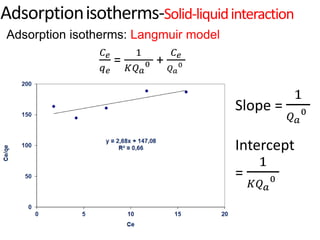
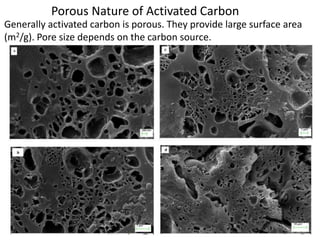
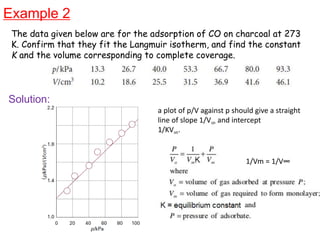
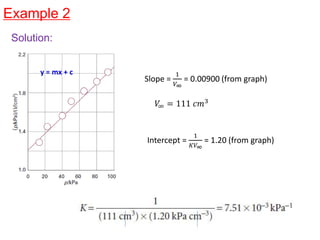
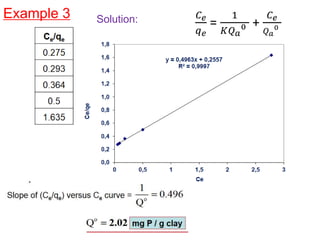
The document discusses various topics related to states of matter and adsorption isotherms. It begins by explaining the particulate theory of matter proposed by Democritus and developed by Dalton. It then describes the three traditional states of matter - solid, liquid, and gas - and how their properties, such as density, differ. A fourth state of matter, plasma, is also introduced. The document then discusses adsorption isotherms and models such as Langmuir and Freundlich isotherms that describe the relationship between gas or liquid concentration and adsorption. Examples are provided to illustrate applying these isotherm models.

1. CHY1009 ; Module 2
-States of mater and adsorption isotherms

2. Sates of mater

3. The Physical States of Matter - Particulate
theory of matter
Greek philosopher Democritus described matter as made up of tiny
microscopic particles.
the particulate theory of matter was first presented by Democritus
in 400 BC
Traditionally there are three states of matter

4. John Dalton who is credited with first developing the modern
atomic theory of matter in the early 1800s.
The theory presented by Democritus was predominately a
philosophical statement and therefore not widely accepted.
In contrast, Dalton’s theory was based on careful experimental
observations and measurements and so became the first atomic
theory of matter founded on scientific concepts and principles.
According to the modern atomic theory, matter can be classified
according to both its physical and chemical state
The Physical States of Matter - Particulate
theory of matter

5. The Physical States of Matter - Particulate
theory of matter

6. Physical States of Mater- Properties
Gas Liquid Solid
These characteristics affect the physical properties of matter,
such as volume occupancy, density, light scattering, etc.,

7. Interparticle distance decreases, this decreases volume.
Density (ρ ) ∝ 1/Volume (V)
Density (mass/cm3) of Gas, Liquid, Solids
ρ = mass/unit volume = M/V
For a given mass of substance, density increases while going
from gas-to-liquid and liquid-to-solid.

8. Solid
(g/cm3)
Liquid (g/cm3)
Gas
(g/cm3)
Ar 1.65 1.40 0.001784
N2 1.026 0.8081 0.001251
O2 1.426 1.149 0.001429
Density (mass/cm3) of Gas, Liquid, Solids - Examples
-the density of a typical solid is about 20% larger than the
corresponding liquid,
-while the liquid is roughly 800 times as dense as the gas.

9. Plasma – 4th states
of Matter
• Plasma is a “superheated matter”
comprised of ions formed from atoms or
molecules by striping of at least one electron.
• It comprises over 99% of the visible universe.
• In the night sky, plasma glows in the form of
stars, nebulas, and even the auroras that
sometimes ripple above the north and south
poles.
• Plasma is often called “the fourth state of
matter,” along with solid, liquid and gas.

10. https://www.nasa.gov/sites/default/files/thumbnails/image/147515main_phases_large.jpg

11. Adsorption isotherms
Surface chemistry is the study of processes that occur
at the interface of two bulk phases.
Bulk phase may be a solid or liquid or gas
Liquid- liquid

12. Interaction Open Surfaces
solid with Gases
Phenomena of Adsorption
Adsorbate
Adsorbent
Except in special cases, adsorption is an exothermic process,
releases heat to the surrounding.
Enthalpy change is negative ∆Had = -Ve
The phenomena of interaction of a gas or liquid, or ionic species
with a solid surface is referred as adsorption.
Adsorptive

13. Examples of Adsorption
 (i) Adsorption of O2, H2, CO, Cl2, NH3 or SO2 on surface of charcoal,
 (ii) In a solution of an organic dye, say methylene blue on the
surface of charcoal, i.e., are adsorbed.
 (iii) Aqueous solution of raw sugar, when passed over beds of
animal charcoal, becomes colourless as the colouring substances
are adsorbed by the charcoal.
 (iv) The air becomes dry in the presence of silica gel because the
water molecules get adsorbed on the surface of the gel.
The process of removing an adsorbed substance from a surface
on which it is adsorbed is called desorption.

14. The attractive interaction can be either long range or short
range
1. Long range interaction: Physical contact, due to Van der
Waals force.
2. Short range interaction: Chemical bonding, such as covalent,
ionic, metallic bonding
What kind of bonding interaction occurs
between adsorbent and adsorbate?
Accordingly, the first one is called physisorption (Physical adsorption)
and the second one is called chemisorption (Chemical adsorption).

15. Sticking of benzene-like molecules, for example coronene,
on the surface of gold (111) is an example of physisorption.
Example of Physisorption
Surface of gold atoms
Coronene

16. a) Metal surface (adsorbent)
b) Physisorption of H2 through van der Waals interaction
c) Chemisorptions of H2 through M-H bond (metal hydrides)
d) Chemisorbed H atom may slid into the bulk metal through diffusion
Example of Chemisorption
http://cdn.intechopen.com/pdfs-wm/40231.pdf
“Chemisorption always accompanied by physisorption”
Metal hydride is formed through
chemical bonding, hence,
chemisorption.

17. Thermodynamic Considerations
• Adsorption (or any) spontaneous process
requires ∆G < 0. Because the translational freedom
of the adsorbate is reduced when it is adsorbed, ∆S
is negative.
• Therefore, in order for ∆G = ∆ H − T∆S to be
negative, ∆H must be negative (that is, the process is
exothermic).
• Exceptions may occur if the adsorbate dissociates
and has high translational mobility on the surface.

19. Enthalpies of Physi- and Chemisorption
Exothermic reactions, enthalpy change is negative
Enthalpies of chemisorption are greater than enthalpies of
physisorption. These enthalpies are close to covalent bond enthalpies.

20. Vs

21. Quantitative Models on
Adsorption
Amount of gas adsorbed on a solid depends on T and P (or
concentration of solution species) of the gas in contact with the
solid surface.
The amount of gas adsorbed on the solid surface is studied at
constant temperature.
The plot of amount of gas adsorbed as a function of pressure is
known as adsorption isotherm.
This behavior can be explained by empirical or theoretical models.

23. Langmuir Adsorption Isotherm
A
S (Surface of adsorbent)
1. Surface of the adsorbent is homogeneous
2. It has Nactive sites
3. The fraction of sites adsorbed θ = Na/N
4. Surface only allows the formation of monolayer
5. There is no intermolecular interaction between adsorbate
Adsorptive, A(g)
𝑜𝑟 𝜃 =
number of adsorption sites occupied
number of adsorption sites available

24. Adsorptionisotherms-Solid-Gasinteraction
Deriving the Langmuir isotherm
You need to consider the dynamic equilibrium between the molecules
(A) in the gas phase and those on the surface (denoted AM):
rate of adsorption
rate of desorption
At equilibrium there is no net change in θ, implying that the sum of these two rates must be
zero:
at equilibrium
p partial pressure
N is the total number of sites

25. Adsorptionisotherms-Solid-Gasinteraction
Deriving the Langmuir isotherm
At equilibrium there is no net change in θ, implying that the sum of these two rates must be
zero:
at equilibrium
solving for θ gives the Langmuir isotherm
( Some text books use α instead of K)
Langmuir isotherm

26. Adsorptionisotherms-Solid-Gasinteraction
Langmuir isotherm
Langmuir isotherm

27. where,
x = mass of adsorbate
m = mass of adsorbent

28. This model is inadequate to explain some cases of adsorption.
In certain cases the adsorption continues even
after the point of Freundlich saturation limit. (for example liquid
condensation).
Point of saturation

29. Adsorptionisotherms-Effectof T
Lower the T more the surface coverage (adsorption)

30. Continued….
kf approximately indicates adsorption capacity
1/n is a function of the strength of adsorption
n varies with the nature of the adsorbent and
range for favorable adsorption is of 1-10.
1/n = 0, x/m = constant, the adsorption is
independent of pressure.
1/n = 1, x/m = k P, i.e. x/m ∝ P, the adsorption
varies directly with pressure.
30
𝑥
𝑚
= 𝑘 𝑝
1
𝑛

31. Limitations of Freundlich Isotherm
Freundlich equation is purely empirical and
has no theoretical basis.
The equation is valid only upto a
certain pressure and invalid at higher
pressure.
Freundlich's adsorption isotherm fails at
high concentration of the adsorbate.
31

32. Differences between Freundlich and
Langmuir adsorption isotherms
32
FRENDLICH ADSORPTION
ISOTHERM
• Tells about the quantity of
gas adsorbed by unit mass
of solid adsorbent with
pressure.
• Represented by formula
x/m = KP1/n
LANGMUIR ADSORPTION
ISOTHERM
• Tells about the number
of active site undergoing
adsorption and pressure.
• Represented by formula
θ = 𝐾𝑃
1+ KP

33. Adsorptionisotherms-Solid-liquidinteraction
where
qe = mass of material adsorbed (at equilibrium) per mass of adsorbent, mg adsorbate/g
adsorbent
C0 = initial concentration of adsorbate, mg/L
Ce = equilibrium concentration in solution when amount adsorbed equals qe, mg/L
V = volume of liquid in the reactor, L
m = mass of adsorbent, g
mass balance equation
for adsorption

34. kf and n are system specific constants.
Adsorption isotherms: Freundlich isotherm
For the special case that the surface energies are heterogeneous
(particularly good for mixed adsorbates) in which the energy term,
“kF”, varies as a function of surface coverage, the Freundlich
model is appropriate.
The model equation is:
Adsorptionisotherms-Solid-liquidinteraction
𝑞𝑒 = 𝑘𝑓𝐶𝑒
1
𝑛

35. q
e
Ce
Shape of the Freundlich isotherm changes upon changing the
values of n and k

36. 0
a e
e
e
K Q C
q
1 K C
 

 
0
a
Q represents the maximum adsorption capacity
(monolayer coverage) (g solute/g adsorbent).
Ce has units of mg/L
K Langmuir equilibrium constant has units of
L/mg
Adsorption isotherms: Langmuir model
This model assumes monolayer coverage and constant binding
energy between surface and adsorbate.
The model equation is:
Adsorptionisotherms-Solid-liquidinteraction
⇒ 𝐶𝑒
𝑞𝑒
=
1
𝐾𝑄𝑎
0 +
𝐶𝑒
𝑄𝑎
0

37. Adsorption isotherms: Langmuir model
Adsorptionisotherms-Solid-liquidinteraction
𝐶𝑒
𝑞𝑒
=
1
𝐾𝑄𝑎
0 +
𝐶𝑒
𝑄𝑎
0
Slope =
1
𝑄𝑎
0
Intercept
=
1
𝐾𝑄𝑎
0

38. Application of Adsorbents
• Organic contaminants such as pharmaceuticals, cosmetics,
pesticides can be removed from water using the method of
adsorption.
• To speed up chemical reactions (catalysis)
• To remove bad odor and color in water
• Used as a solid support purify proteins and chemical
compounds
• Used to remove unwanted impurities from gas
38

39. • Uses
Remove man-made organic chemicals
Remove miscellaneous tastes and
odor from water assuming no bacterial
problems
Remove radon gas from water
• Maintenance
Carbon must be replaced routinely
Uses of activated carbon as a adsorbent

41. Porous Nature of Activated Carbon
Generally activated carbon is porous. They provide large surface area
(m2/g). Pore size depends on the carbon source.

42. Example 1
Adsorption of benzene onto activated carbon has been reported
to obey the following Freundlich isotherm equation, where c is in
mg/L and q is in mg/g:
A solution at 25o
C containing 0.50 mg/L benzene is to be treated
in a batch process to reduce the concentration to less than
0.01 mg/L. The adsorbent is activated carbon with a specific
surface area of 650 m2/g.
Compute the required activated carbon dose.
0.533
50.1
benz benz
q c

Problems

43. Example 1
Solution:
𝐶0 = 0.5 𝑚𝑔/𝐿
𝐶𝑒 = 0.01 mg/L
𝑞𝑒 = ?
𝑚
𝑉
= ?
𝑞𝑒 = 𝑘 𝐶𝑒
1/𝑛
0.533
50.1
benz benz
q c

𝑞𝑒 = 50.1 (0.01)0.533
𝑞𝑒 = 4.30 𝑚𝑔/𝑔

44. Example 1
Solution:
𝐶0 = 0.5 𝑚𝑔/𝐿
𝐶𝑒 = 0.01 mg/L
𝑞𝑒 = 4.30 mg/g
𝑚
𝑉
= ?
𝑚
𝑣
=
𝐶0 − 𝐶𝑒
𝑞𝑒
𝑚
𝑣
=
0.5 − 0.01
4.3
𝑚
𝑣
= 0.114 g/L
mg/g
mg/L

45. Example 2
The data given below are for the adsorption of CO on charcoal at 273
K. Confirm that they fit the Langmuir isotherm, and find the constant
K and the volume corresponding to complete coverage.
Solution:
a plot of p/V against p should give a straight
line of slope 1/V∞ and intercept
1/KV∞.
1/Vm = 1/V∞

46. Example 2
Solution:
Slope =
1
𝑉∞
= 0.00900 (from graph)
𝑉
∞ = 111 𝑐𝑚3
Intercept =
1
𝐾𝑉∞
= 1.20 (from graph)
y = mx + c

47. Example 3
Determine the maximum P adsorption capacity of this clay
(mg P / g clay).

48. Example 3 Solution: 𝐶𝑒
𝑞𝑒
=
1
𝐾𝑄𝑎
0 +
𝐶𝑒
𝑄𝑎
0