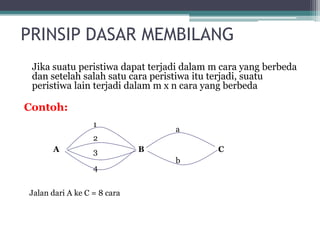
Dokumen ini membahas prinsip dasar kombinatorika dan faktorial dalam konteks penghitungan jumlah kemungkinan hasil dari suatu peristiwa. Terdapat beberapa contoh soal serta definisi faktorial yang diilustrasikan dengan perhitungan. Penjelasan mencakup berbagai skenario, seperti bilangan yang dapat disusun dan cara masuk-keluar dari gedung.

1. PRINSIP DASAR MEMBILANG DAN
FAKTORIAL
Prodi S.1 PGMI/SD STAI Al-Ihya Kuningan

2. PRINSIP DASAR MEMBILANG
Jika suatu peristiwa dapat terjadi dalam m cara yang berbeda
dan setelah salah satu cara peristiwa itu terjadi, suatu
peristiwa lain terjadi dalam m x n cara yang berbeda
Contoh:
1
a
2
A 3 B C
b
4
Jalan dari A ke C = 8 cara

3. Contoh :
1. Berapa banyak bilangan yang terdiri dari dua angka
dapat disusun dari angka-angka 0,1,2,3 dan 4
2. Berapa banyak bilangan yang terdiri dari tiga angka
dapat disusun dari angka-angka 2, 4, 6, dan 8 jika angka-
angka itu :
a. Boleh muncul berulang
b. tidak boleh mengulang
3. Gedung serbaguna mempunyai 3 pintu. Dengan berapa
cara seseorang dapat masuk dan keluar dari gedung itu,
jika:
a. Pintu masuk dan keluar sama
b. Pintu masuk dan keluar tidak sama

4. FAKTORIAL
Definisi:
n ! = perkalian n unsur bilangan asli berturutan
= 1.2.3.4.5.6. … .n
= n.(n-1).(n-2).(n-3). … . 3.2.1
1! = 1
0! = 1
Contoh :
4 ! = 4.3.2.1 = 24
6 ! = 6.5.4.3.2.1 = 720

5. Selesaikan
1. 10! 7. n!
2. (10 – 3)! (n-2)!
3. 10! – 3! 8. (n+2) !
4. (4 + 2)! (n-2) !
5. 4! + 2!
6. 5!
3!

6. Hatur Nuhun