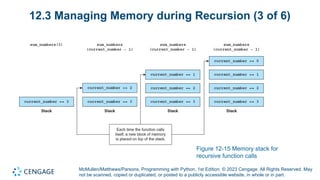
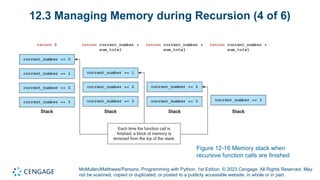
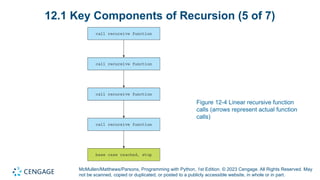
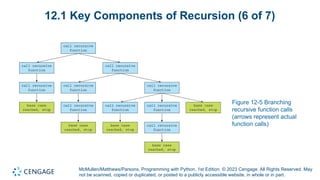
Module 12 of 'Programming with Python' focuses on recursion, including its definition, key components, and applications. It explains how recursion can break down complex problems into simpler ones and highlights the importance of managing memory during recursive calls. The module also differentiates between linear and branching recursion, providing examples and guidelines for designing recursive functions.















![McMullen/Matthews/Parsons, Programming with Python, 1st Edition. © 2023 Cengage. All Rights Reserved. May
not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.
12.2 Using Recursion to Solve Complex Problems
(5 of 7)
• Branching recursion
• Problems that are more complicated than an iterative design can handle may be solved
with branching recursion
• Functions called by the following sample branching recursive function, which counts files
with a .txt extension in a folder and its subfolders
• os.listdir("folder"): returns a list of files in the folder
• os.path.isdir("filename"): returns True if "filename" is a folder
• os.path.join(["folder", "filename"]): returns a folder name and file
name as a path
• "filename".endswith("extension"): returns True if the file name ends with
the extension](https://image.slidesharecdn.com/mcmullenprogwpython1emod12powerpoint-241108235515-18a8358d/85/McMullen_ProgwPython_1e_mod12_PowerPoint-pptx-18-320.jpg)