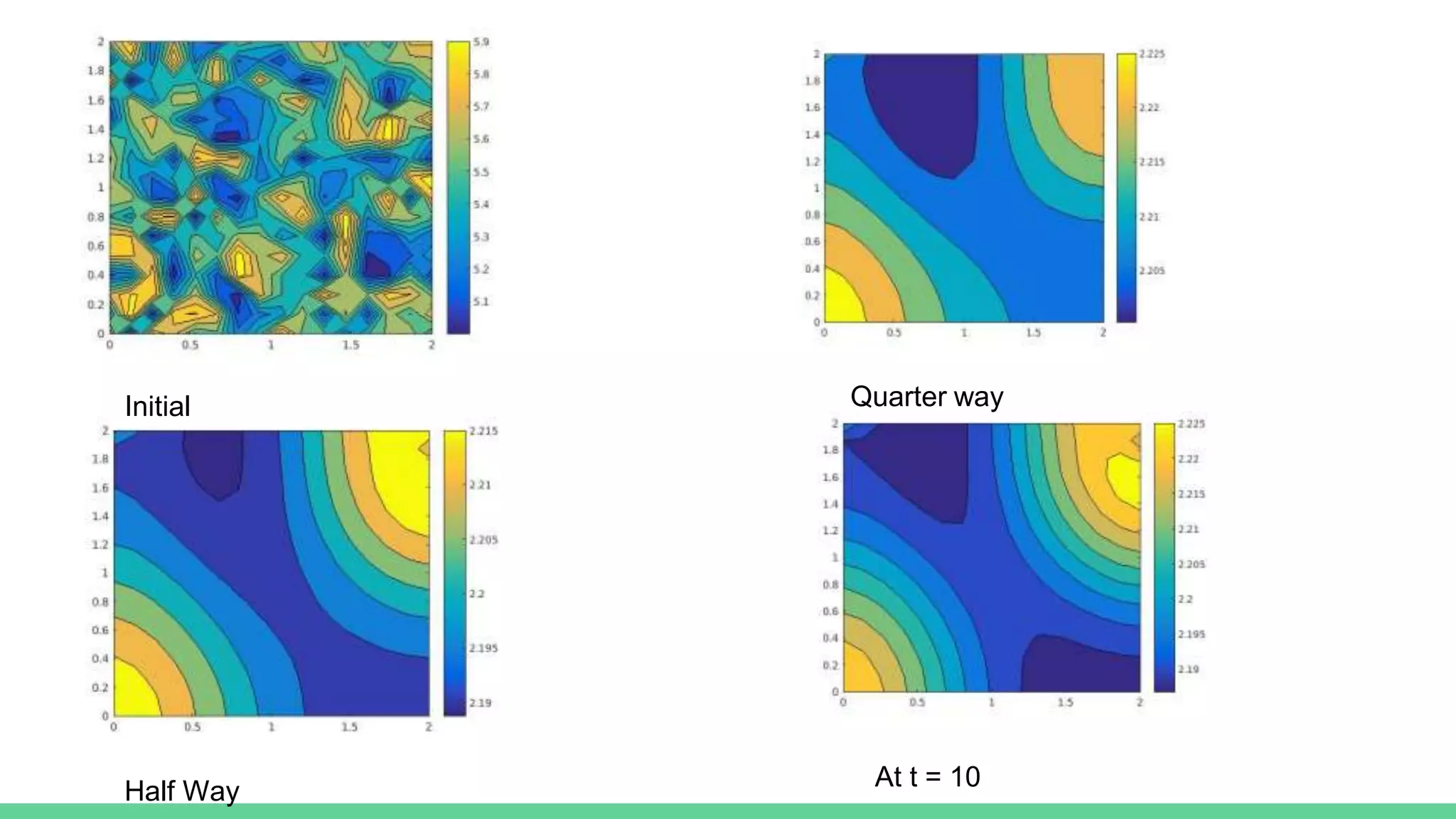
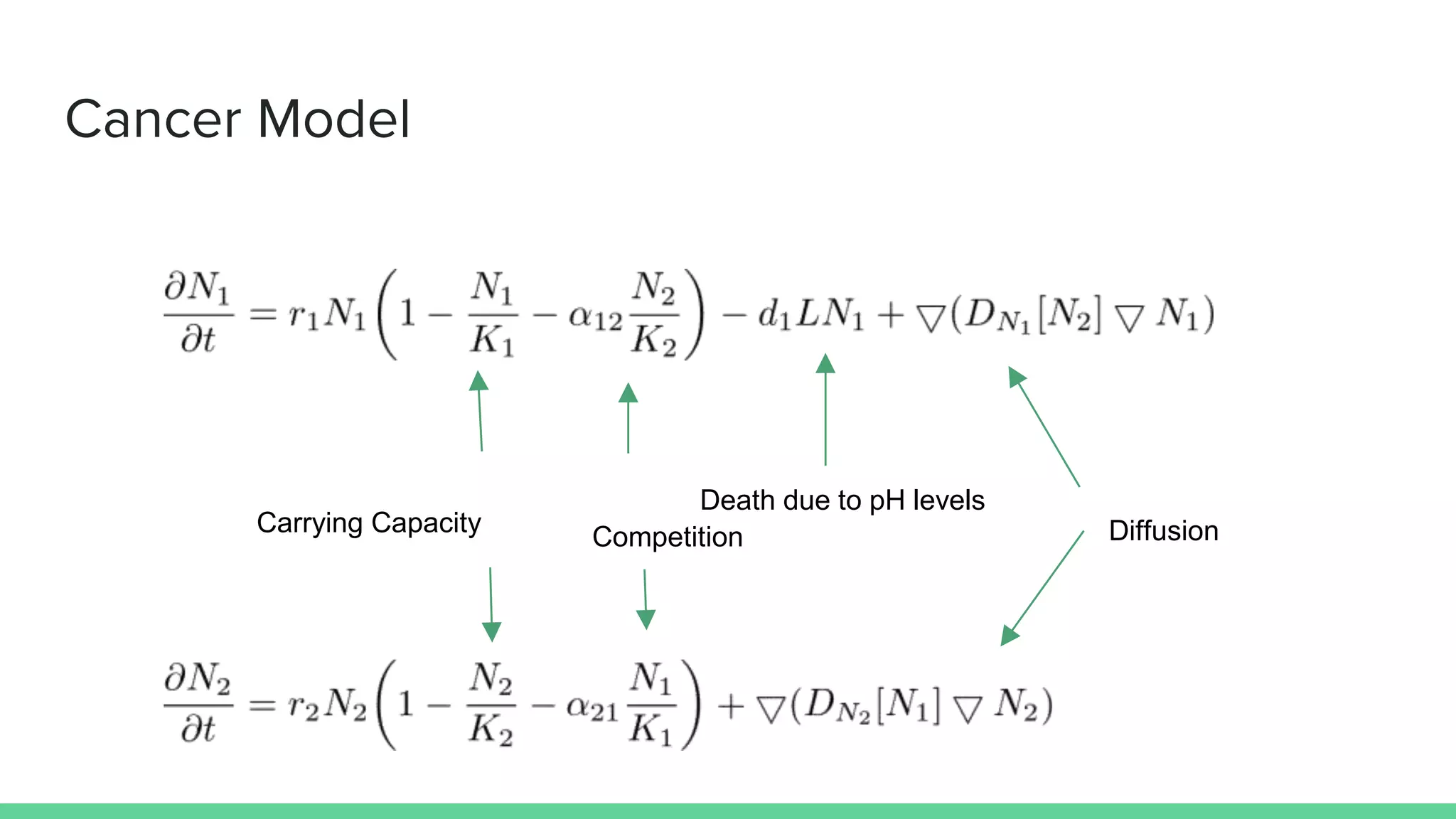
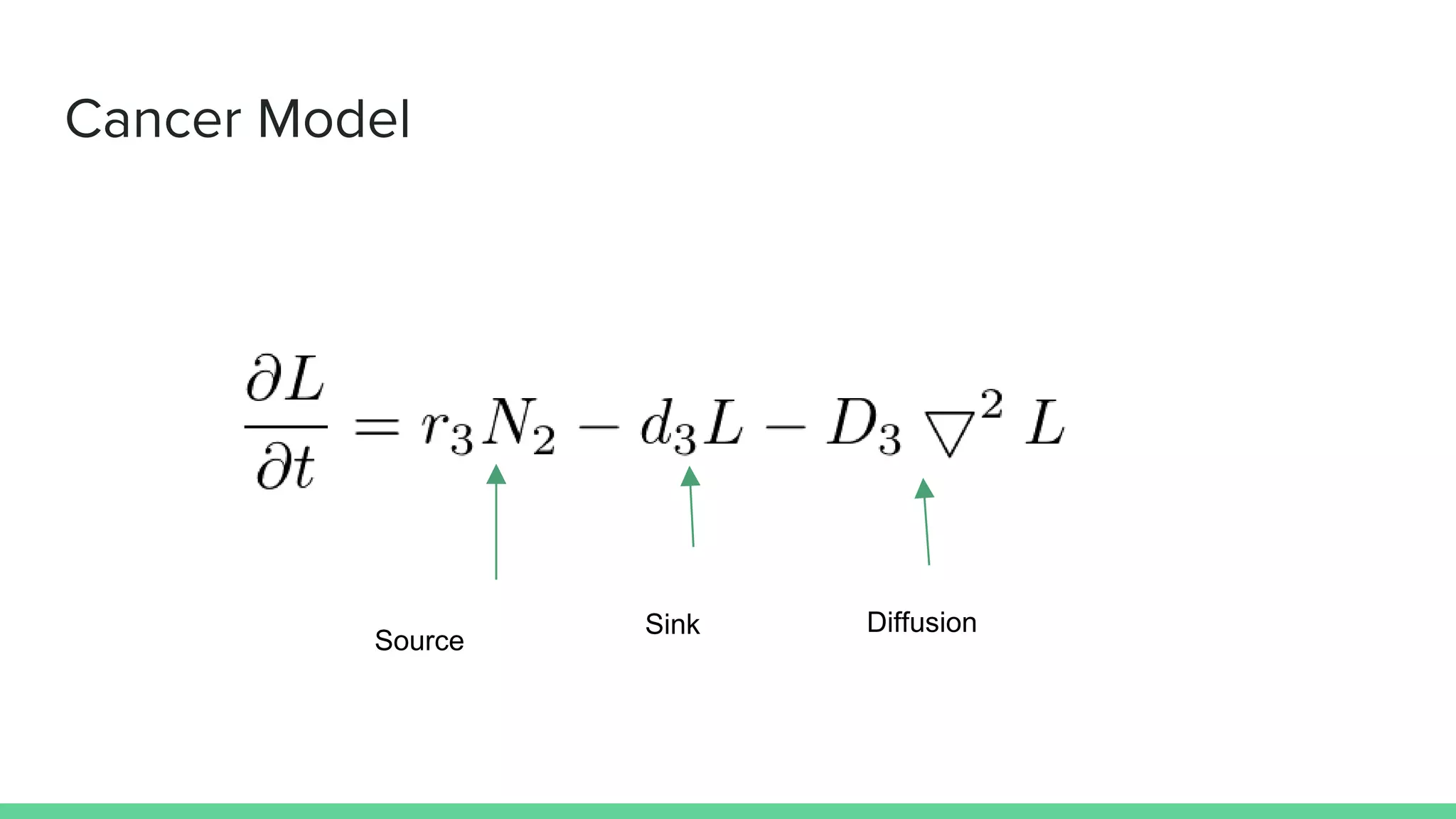
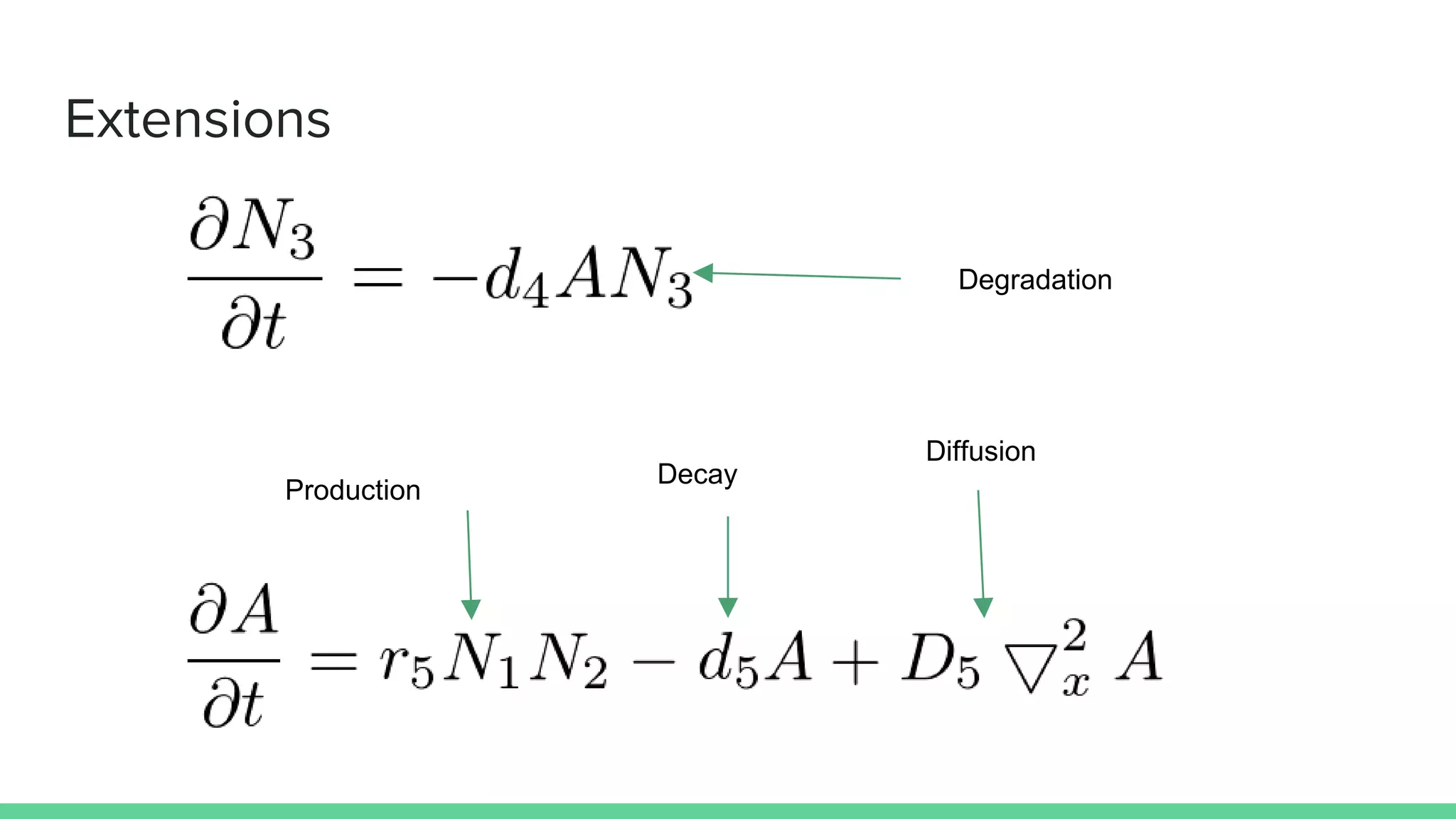
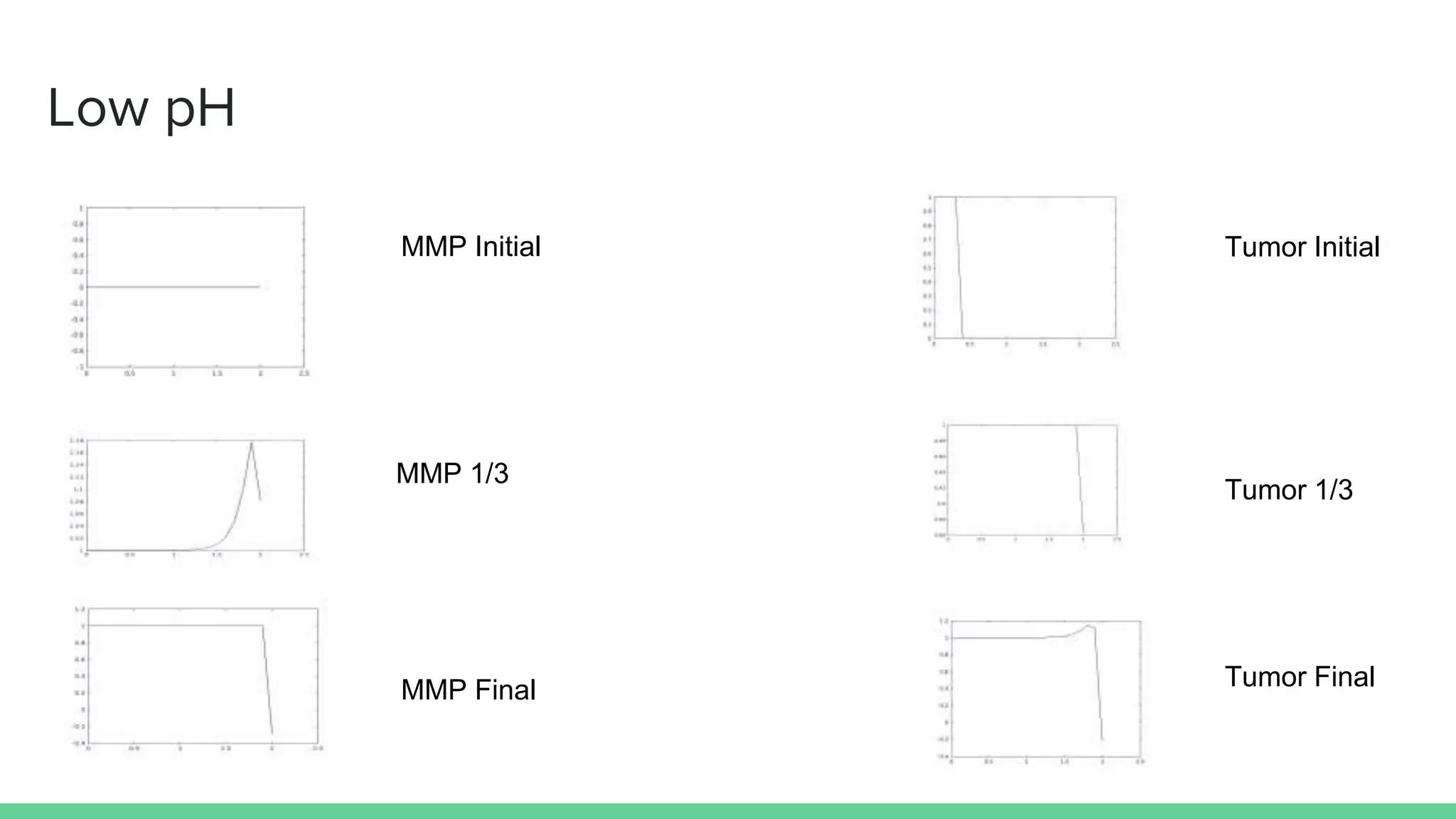
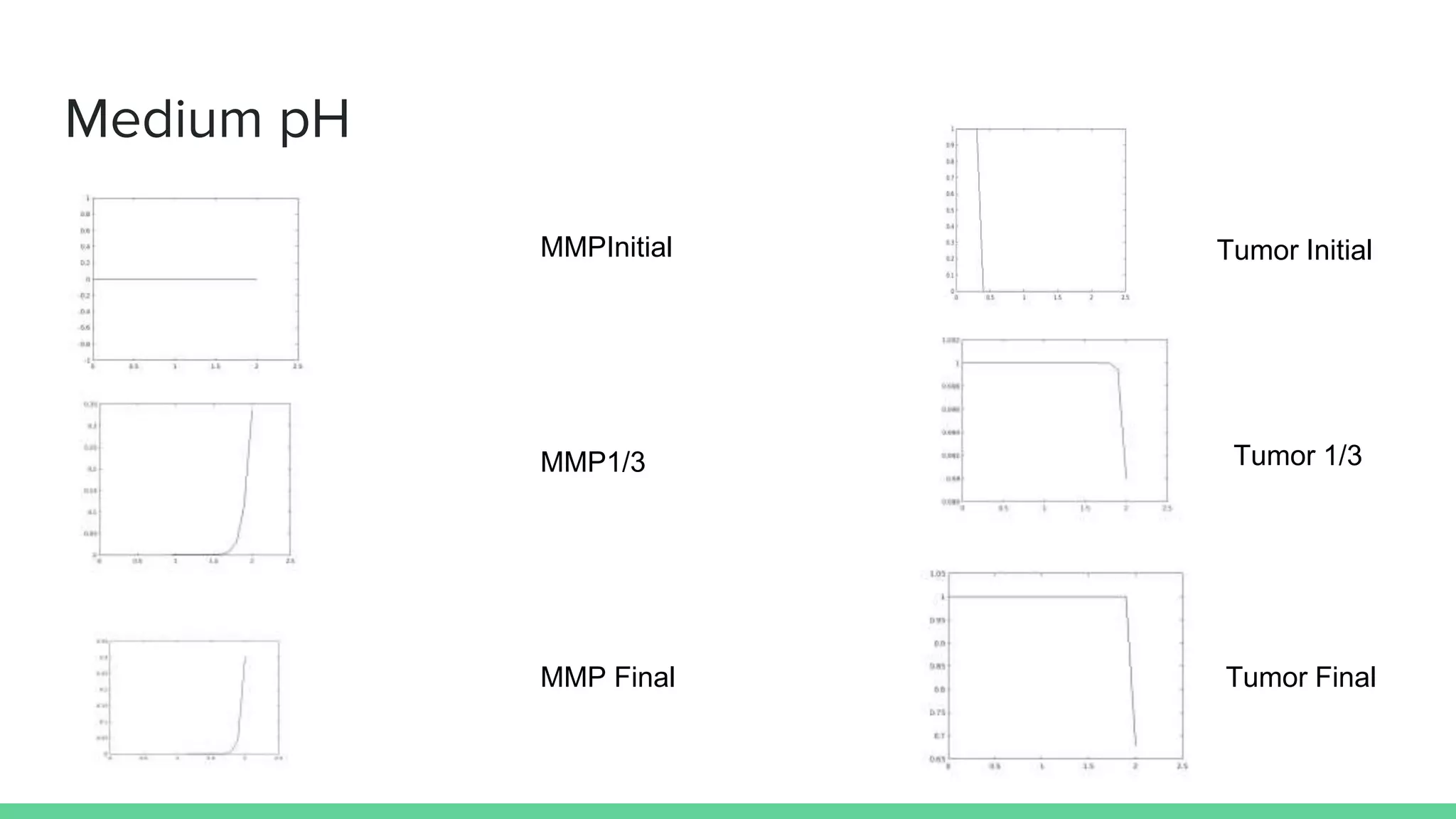
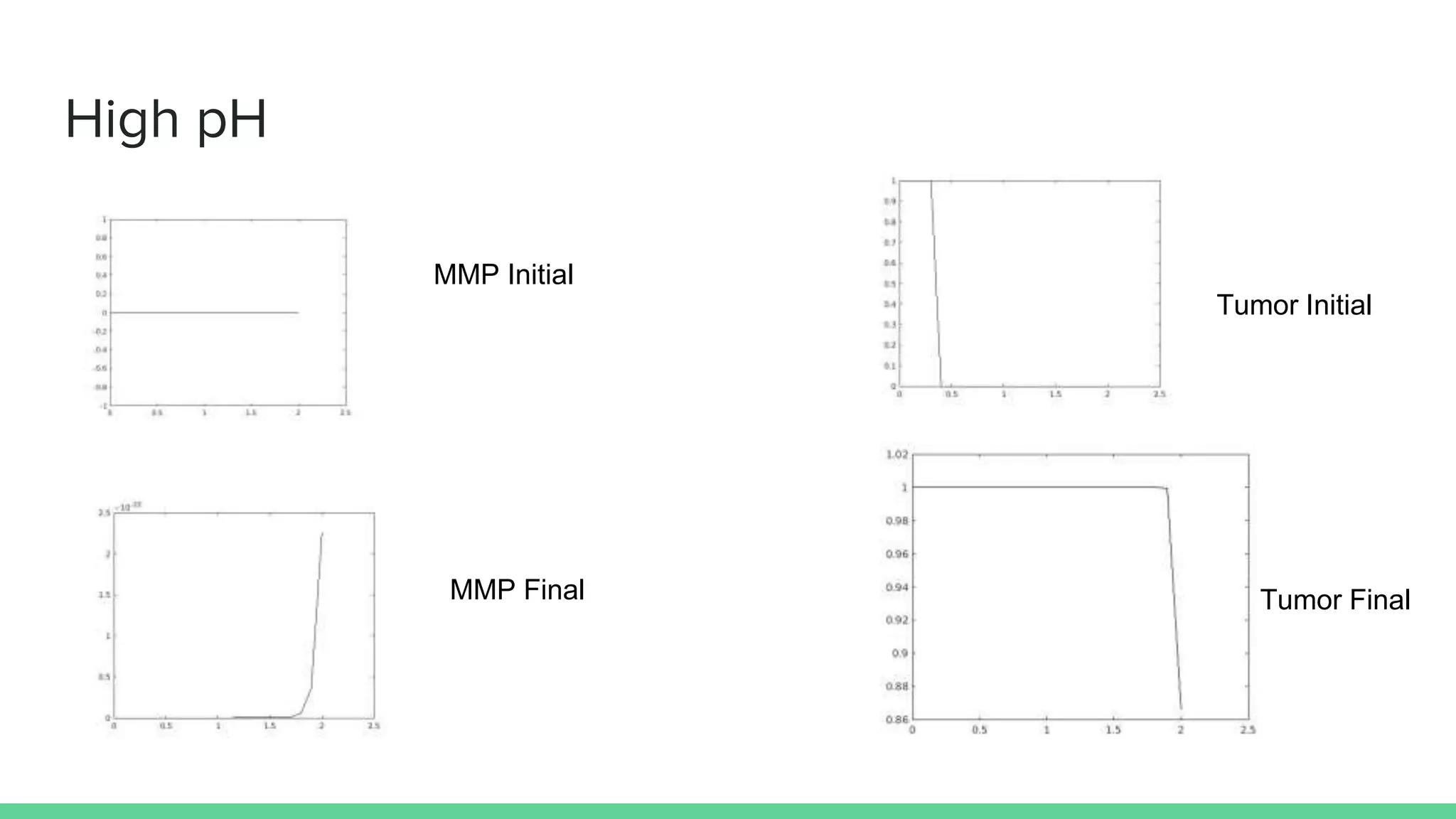
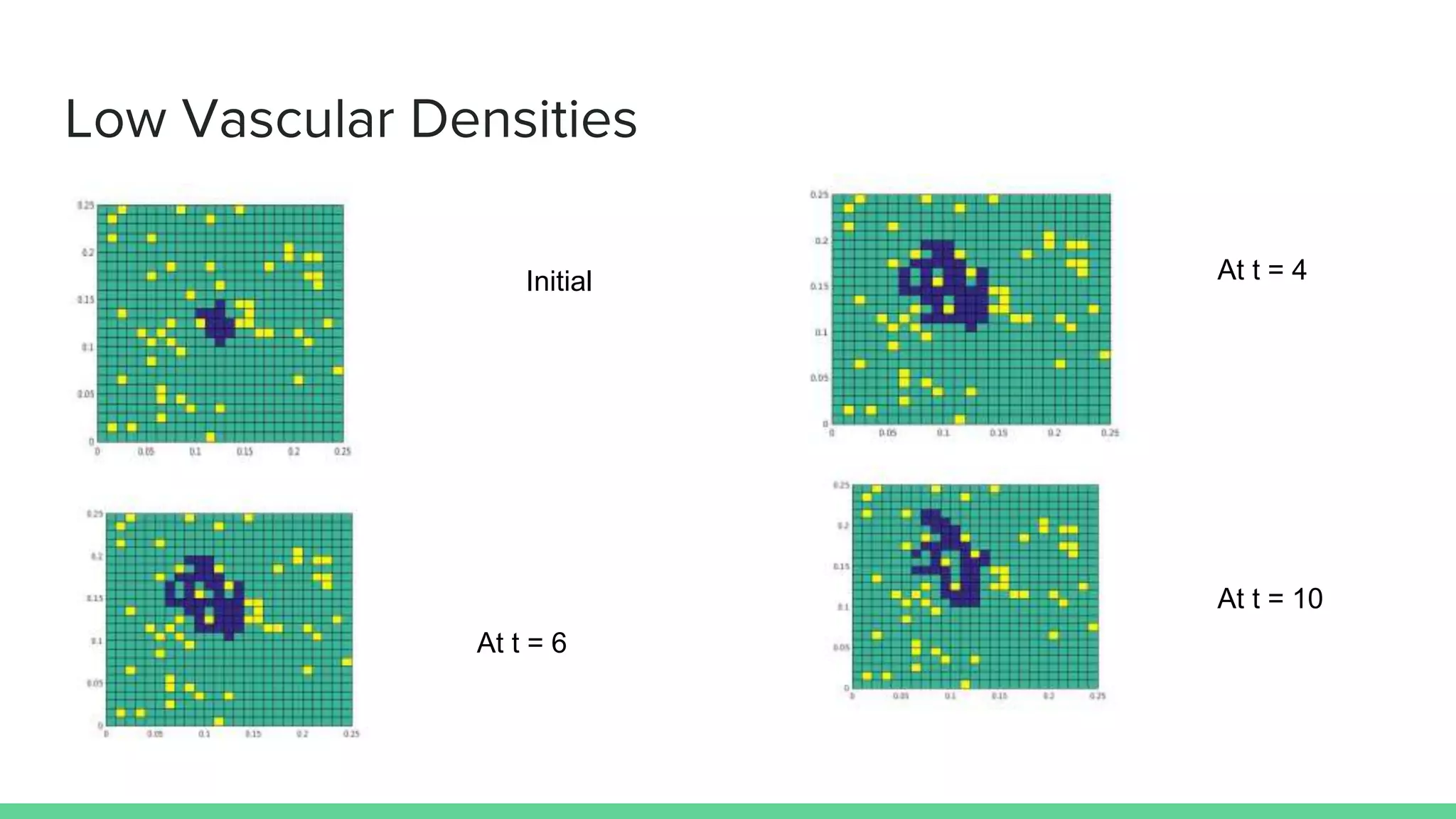
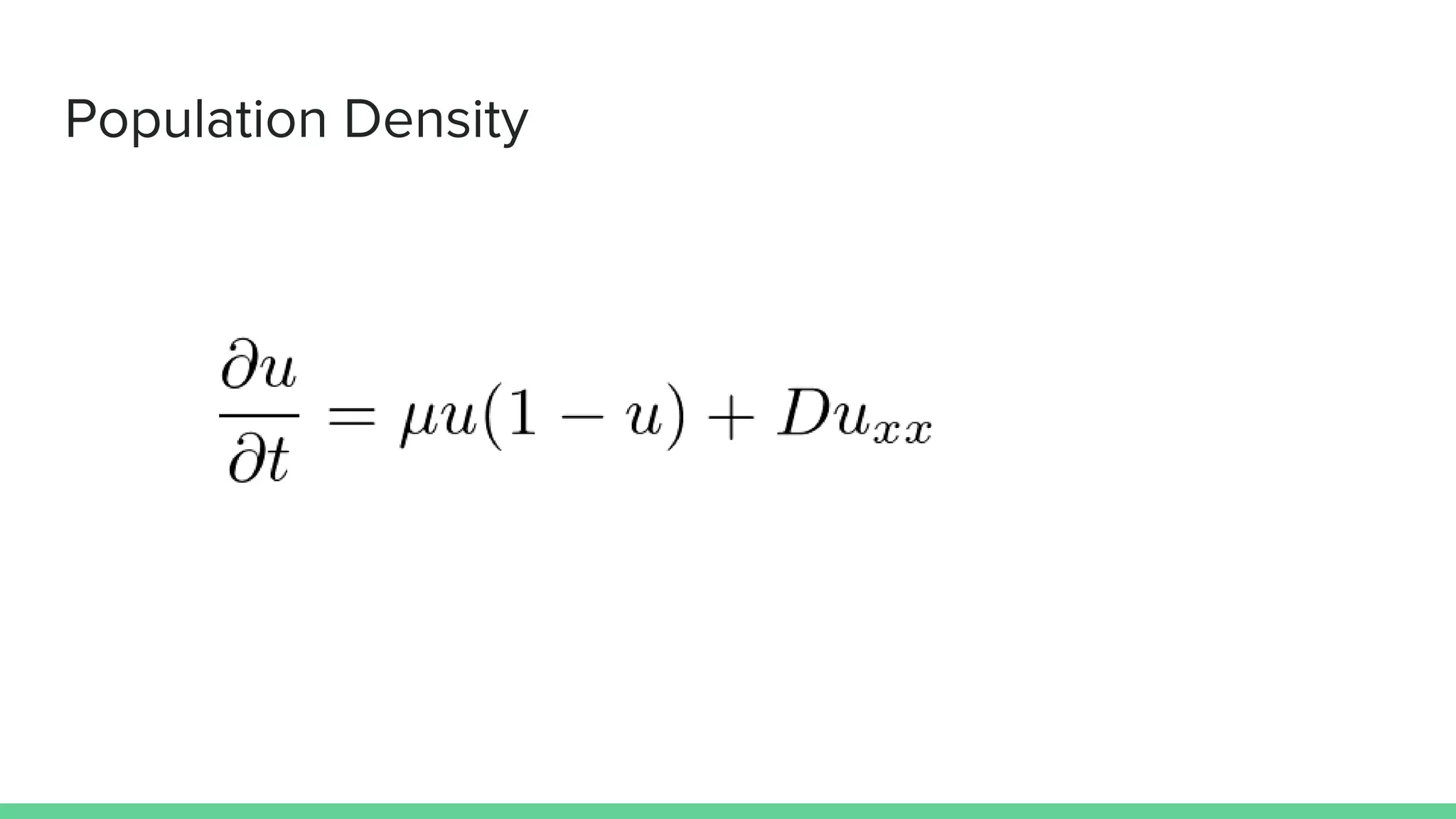The document discusses mathematical models of tumor invasion and growth. It examines both cellular automata models that model tumor invasion at the individual cell level, and continuous reaction-diffusion models that model tumor growth across tissues. Key aspects covered include modeling the effects of acidity levels, glucose and hydrogen concentrations, vascularization, and how tumors can transform and invade surrounding areas. Simulation results demonstrate how tumors can spread over time at different vascular densities and pH levels according to the mathematical models.