Dokumen ini membahas metode numerik untuk integral, termasuk teknik pendekatan seperti Newton-Cotes, Trapesium, dan Simpson. Penekanan utama adalah pada pentingnya integrasi numerik untuk menyelesaikan integral yang sulit secara analitik dan bagaimana kesalahan dapat diminimalkan dengan meningkatkan orde metode. Contoh praktis juga diberikan untuk menerapkan metode Trapesium dalam menghitung nilai integral.

1. METODE NUMERIK
INTEGRAL NUMERIK
http://maulana.lecture.ub.ac.id

2. Definisi
 mengintegrasikan = memadukan bersama = menjumlahkan total
 Mengapa ada integrasi numerik?
Karena integrasi numerik digunakan untuk menyelesaikan
integral yang sulit diselesaikan secara analitik
x
f(x)
f(x)
b
a

b
a
dx
x
f )
(

3. Jenis integral Numerik
 Newton-Cotes
 Trapesium
 Simpson
 Romberg
 Fox-Romberg
 Gauss-Legendre
 Gauss-Chebyshev
 Gauss-Hermite
 Double Exponential

4. Definisi
 Contoh :
 sulit diselesaikan secara analitis (dengan
teori kalkulus yang ada)
 
 

2
0
1
2
2
1
dx
x
e
x x

5. Cara Penyelesaian
 Melalui pendekatan kurva
x f(x)
0 . . . . .
0,25 . . . . .
0,5 . . . . .
0,75 . . . . .
. . . . .
. . . . .
2 . . . . .
Semakin kecil selang, hasil semakin teliti karena
semakin besar selang, kesalahan semakin besar

6. Cara Penyelesaian
 Alternatif pemecahan (jika tidak dengan
penyelesaian analitis)
 Memplot grafik tersebut pada kertas berpetak segi
empat (dijumlah luas setiap kotak)
 Membuat segmen-segmen vertikal (mirip diagram
batang), menjumlah (luas setiap segmen vertikal).
 Integrasi numerik

7. Integrasi Newton Cotes
 Perhitungan integrasi numerik yang paling
umum adalah formula Newton Cotes.
 Strategi dari formula ini adalah mengganti
yang rumit atau data yang hilang dengan
beberapa fungsi aproksimasi yang mudah
diintegrasikan.

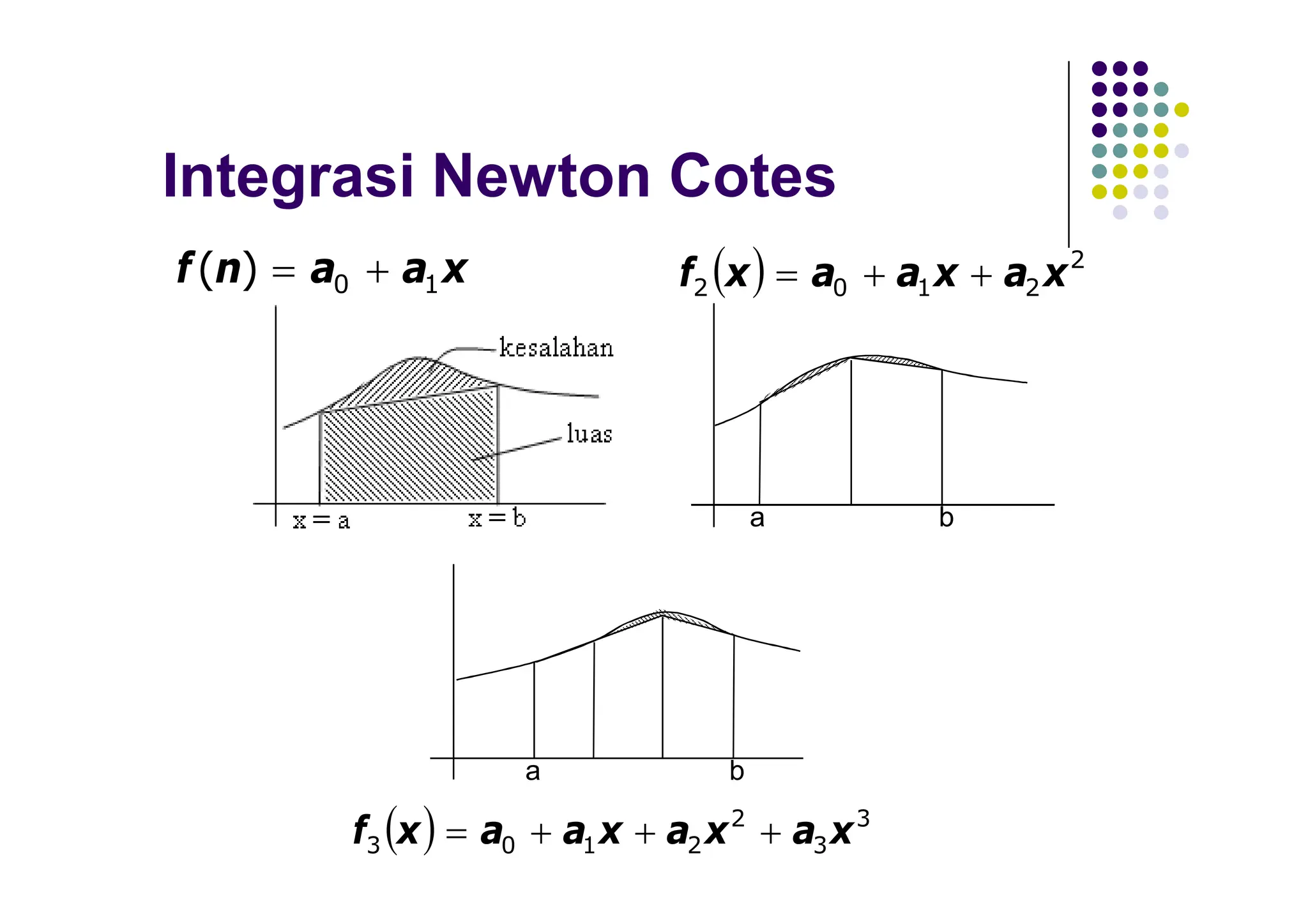
8. Integrasi Newton Cotes
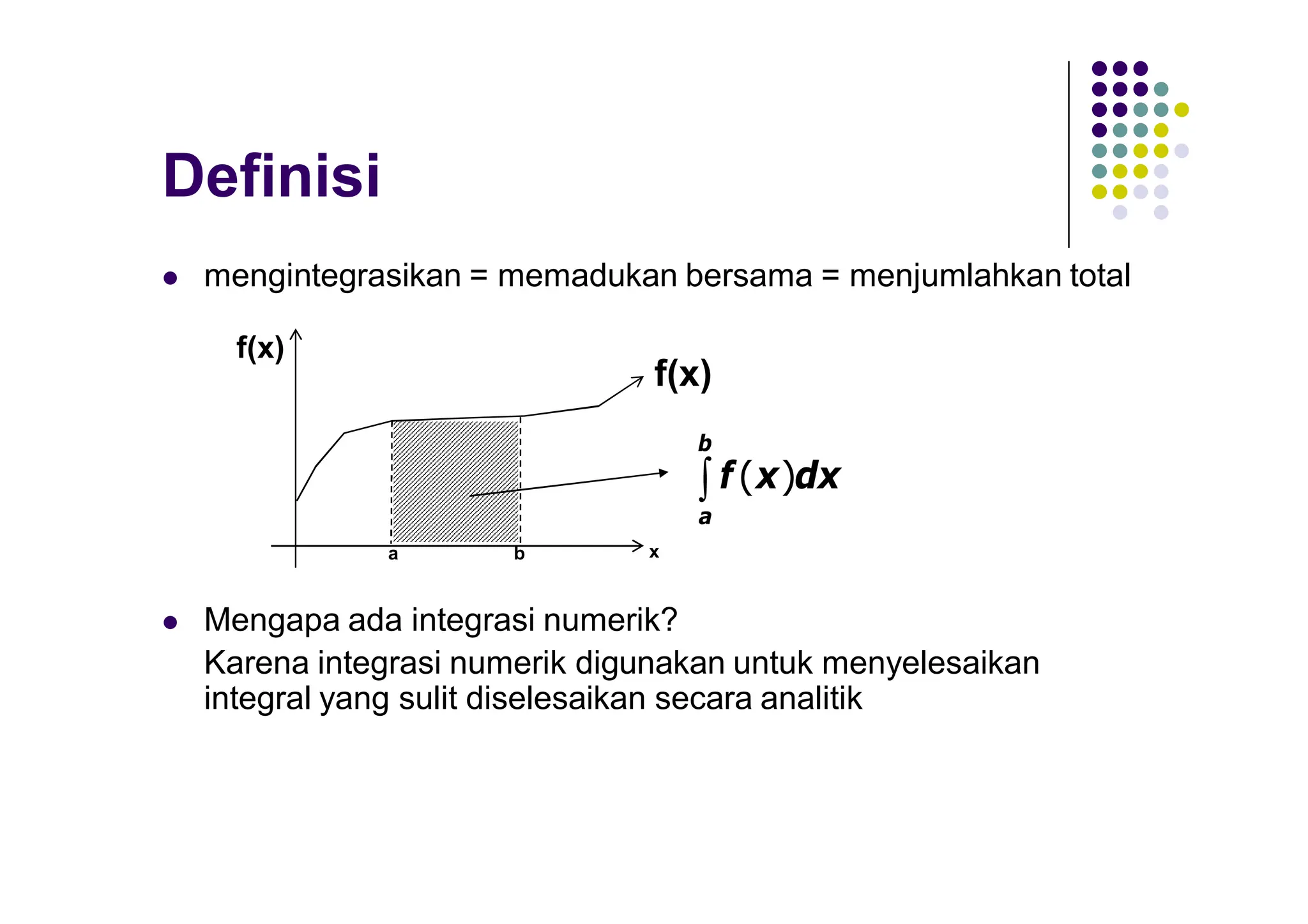
 Jika diketahui suatu f(x) pada interval [a,b],
nilai integral
bisa didekati dengan Newton Cotes orde n.
 Bentuk umum Newton Cotes orde n 


b
a
dx
x
f
s )
(
n
n
n
n x
a
x
a
x
a
x
a
a
n
f 



 

1
1
2
2
1
0
)
( 


9. Integrasi Newton Cotes
b
a
b
a
x
a
a
n
f 1
0
)
( 

  3
3
2
2
1
0
3 x
a
x
a
x
a
a
x
f 



  2
2
1
0
2 x
a
x
a
a
x
f 



10. Integrasi Newton Cotes
 Semakin tinggi orde Newton yang digunakan
sebagai pendekatan perhitungan, akan
semakin kecil kesalahan yang dihasilkan.
 Pendekatan Newton Cotes orde ke-n
 perlu (n+1) titik.
 Dalam formula Newton Cotes
 Metode tertutup  batas awal dan batas akhir
diketahui
 Metode terbuka  batas integrasi diperluas di
luar rentangan (ekstapoksi)

11. Metode Trapesium
 Metode ini adalah bagian dari metode
integrasi Newton tertutup dengan
menggunakan aproksimasi polinomial orde 1,
sehingga dengan aturan trapesium.
 


b
a
dx
x
f
I 1
 Newton Cotes orde 1
     
2
b
f
a
f
a
b
I



 Rumus ini berpadanan dengan
rumus geometri dari trapesium,
dengan lebar sebesar (b–a) dan
tinggi rata-rata    
2
b
f
a
f 

12. Metode Trapesium
 Besarnya kesalahan untuk aturan trapesium
tunggal adalah :
adalah nilai rata-rata dari turunan ke-2
yang dirumuskan sebagai
 3
12
1
a
b
f
a 





f 

 
a
b
x
f
f
b
a





"

13. Metode Trapesium (Ex.)
 Diketahui suatu fungsi
 Hitung nilai analitis dari
 Hitung nilai integral di atas dengan aturan
trapesium tunggal pada batas x = 0 sampai
dengan x = 2
 Hitung nilai t dan a
    x
e
x
x
f 1


 

2
0
dx
x
f

14. Metode Trapesium (Ex.)
 u = x + 1 dv = ex.dx
 du = dx v =
  
 

 du
v
v
u
dx
e
x x
.
.
1
2
0
x
x
e
dx
e 

   
 
 
   
 
0
0
2
2
2
0
2
0
2
0
.
1
0
.
1
2
]
1
]
.
1
1
e
e
e
e
e
e
x
dx
e
e
x
dx
e
x
x
x
x
x
x












 

0
e
e
.
3 2
2



2
e
.
2
 = 14,778
Secara eksak

15. Metode Trapesium (Ex.)
 Dengan aturan trapesium tunggal
     
2
b
f
a
f
a
b
I


 ; b = 2; a = 0
     
     
     167
,
23
2
167
,
22
1
0
2
167
,
22
.
3
.
1
2
2
1
.
1
0
0
2
2
0













I
e
e
f
b
f
e
f
a
f

16. Metode Trapesium (Ex.)
 Kesalahan
%
767
,
56
%
100
778
,
14
167
,
23
778
,
14




t

t (tidak dalam persen)
t = |14,778 – 23,167| = 8,389

17. Metode Trapesium (Ex.)
 a = ?
   
     
     
 
 





















dx
e
x
f
e
x
e
x
e
x
f
e
x
e
x
e
x
f
e
x
x
f
x
x
x
x
x
x
x
x
0
2
.
.
3
.
3
.
2
.
2
.
1
.
1
2
2
0

18. Metode Trapesium (Ex.)
u = x + 3 dv = ex.dx
du = dx
  
 

 du
v
v
u
dx
e
x x
.
.
.
.
3
2
0
 
 x
x
e
dx
e
v .
   
2
0
2
0
]
.
.
3
.
.
3 
 


 dx
e
e
x
dx
e
x x
x
x
 
 
   
 
556
,
27
2
4
2
.
5
.
3
0
.
3
2
]
.
3
2
2
2
0
0
2
2
2
0















e
e
e
e
e
e
e
e
e
x x
x

19. Metode Trapesium (Ex.)
 
 3
.
12
1
778
,
13
0
2
556
,
27
a
b
f
f
a 










  
185
,
9
185
,
9
0
2
.
778
,
13
12
1 3







20. References
Resource:
 http://www2.math.umd.edu/~dlevy/classes/amsc466/lectur
e-notes/integration-chap.pdf
 http://www.mathcs.emory.edu/~haber/math315/chap5.pdf
 http://www.uio.no/studier/emner/matnat/math/MAT-
INF1100/h11/kompendiet/chap12.pdf
Comparation :
 http://www.hvks.com/Numerical/webintegration.html

21. Check hasil integrasi