ブログ用のスライドです。

1. 累積和をmapに入れて
区間の和をカウントする
satanic @satanic0258

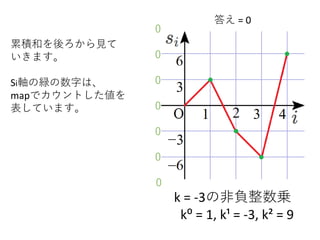
2. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
累積和を後ろから見て
いきます。
Si軸の緑の数字は、
mapでカウントした値を
表しています。
0
0
0
0
0
答え = 0
0
0

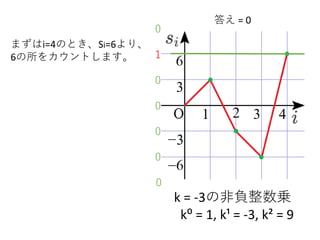
3. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
まずはi=4のとき、Si=6より、
6の所をカウントします。
0
0
0
0
1
答え = 0
0
0

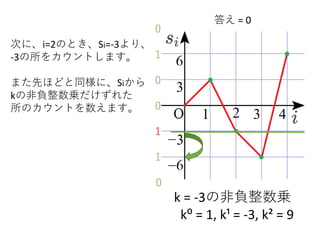
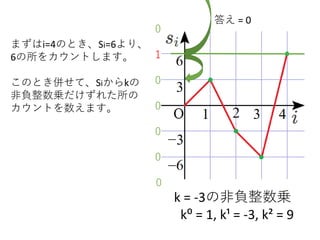
4. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
まずはi=4のとき、Si=6より、
6の所をカウントします。
このとき併せて、Siからkの
非負整数乗だけずれた所の
カウントを数えます。
0
0
0
0
1
答え = 0
0
0

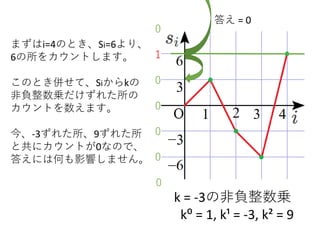
5. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
まずはi=4のとき、Si=6より、
6の所をカウントします。
このとき併せて、Siからkの
非負整数乗だけずれた所の
カウントを数えます。
今、-3ずれた所、9ずれた所
と共にカウントが0なので、
答えには何も影響しません。 0
0
0
0
1
答え = 0
0
0

6. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
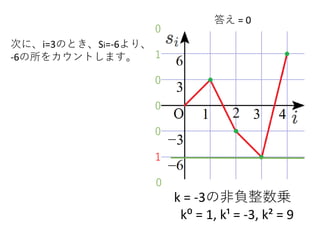
次に、i=3のとき、Si=-6より、
-6の所をカウントします。
1
0
0
0
1
答え = 0
0
0

7. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
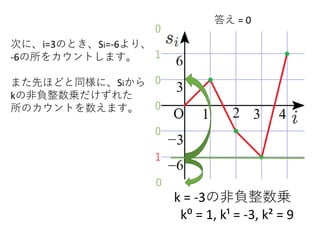
次に、i=3のとき、Si=-6より、
-6の所をカウントします。
また先ほどと同様に、Siから
kの非負整数乗だけずれた
所のカウントを数えます。
1
0
0
0
1
答え = 0
0
0

8. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
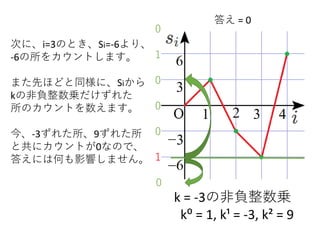
次に、i=3のとき、Si=-6より、
-6の所をカウントします。
また先ほどと同様に、Siから
kの非負整数乗だけずれた
所のカウントを数えます。
今、-3ずれた所、9ずれた所
と共にカウントが0なので、
答えには何も影響しません。 1
0
0
0
1
答え = 0
0
0

9. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
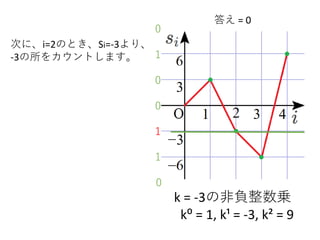
次に、i=2のとき、Si=-3より、
-3の所をカウントします。
1
1
0
0
1
答え = 0
0
0

10. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
次に、i=2のとき、Si=-3より、
-3の所をカウントします。
また先ほどと同様に、Siから
kの非負整数乗だけずれた
所のカウントを数えます。
1
1
0
0
1
答え = 0
0
0

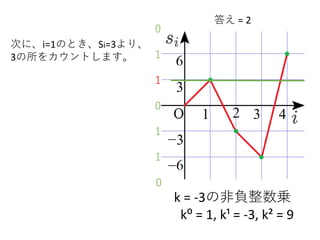
11. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
次に、i=2のとき、Si=-3より、
-3の所をカウントします。
また先ほどと同様に、Siから
kの非負整数乗だけずれた
所のカウントを数えます。
ここで、-3から-3だけずれた
-6には既に1が書き込まれて
います。よって、答えに1を
加えます。
これは、区間[3,3]の和が-3と
なっていることを表して
います。
1
1
0
0
1
答え = 1
0
0

12. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
さらに、-3から9だけずれた
6にも既に1が書き込まれて
います。よって、答えに1を
加えます。
これは、区間[3,4]の和が9と
なっていることを表して
います。
1
1
0
0
1
答え = 2
0
0

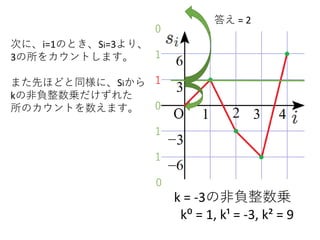
13. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
次に、i=1のとき、Si=3より、
3の所をカウントします。
1
1
0
1
1
答え = 2
0
0

14. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
次に、i=1のとき、Si=3より、
3の所をカウントします。
また先ほどと同様に、Siから
kの非負整数乗だけずれた
所のカウントを数えます。
1
1
0
1
1
答え = 2
0
0

15. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
次に、i=1のとき、Si=3より、
3の所をカウントします。
また先ほどと同様に、Siから
kの非負整数乗だけずれた
所のカウントを数えます。
今、-3ずれた所、9ずれた所
と共にカウントが0なので、
答えには何も影響しません。 1
1
0
1
1
答え = 2
0
0

16. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
次に、i=1のとき、Si=3より、
3の所をカウントします。
また先ほどと同様に、Siから
kの非負整数乗だけずれた
所のカウントを数えます。
今、-3ずれた所、9ずれた所
と共にカウントが0なので、
答えには何も影響しません。
このようにカウントされな
かった場合は、区間[2,j]の和
がkの非負整数乗にならない
ことを表します。
1
1
0
1
1
答え = 2
0
0

17. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
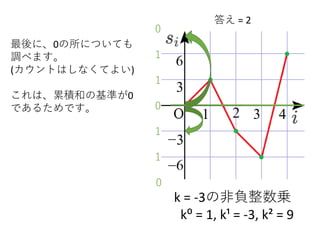
最後に、0の所についても
調べます。
(カウントはしなくてよい)
これは、累積和の基準が0
であるためです。
1
1
0
1
1
答え = 2
0
0

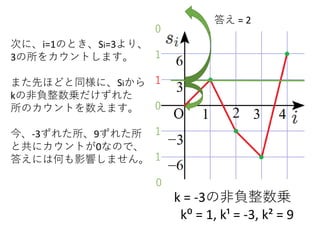
18. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
最後に、0の所についても
調べます。
(カウントはしなくてよい)
これは、累積和の基準が0
であるためです。
今、0から-3だけずれた所に
1が書き込まれていたため、
答えに1加えます。
これは区間[1,2]の和が-3で
あることを表しています。
1
1
0
1
1
答え = 3
0
0

19. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
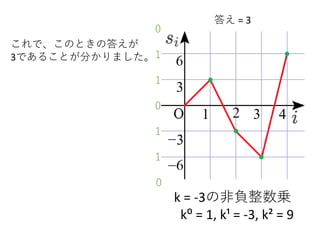
これで、このときの答えが
3であることが分かりました。
1
1
0
1
1
答え = 3
0
0

20. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
これで、このときの答えが
3であることが分かりました。
なお、先ほど
・区間[3,3]の和が-3
・区間[3,4]の和が9
・区間[1,2]の和が-3
であると述べましたが、
この事実はmap上からは
知ることが出来ません。 1
1
0
1
1
答え = 3
0
0

21. k = -3の非負整数乗
k⁰ = 1, k¹ = -3, k² = 9
これで、このときの答えが
3であることが分かりました。
なお、先ほど
・区間[3,3]の和が-3
・区間[3,4]の和が9
・区間[1,2]の和が-3
であると述べましたが、
この事実はmap上からは
知ることが出来ません。
mapにはあくまで累積和の
値が出てきた回数のみを
記録しているためです。
1
1
0
1
1
答え = 3
0
0

22. おわり