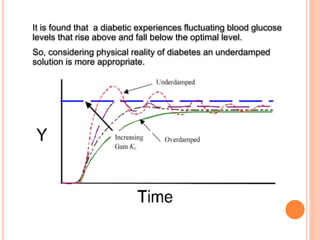
This document presents a mathematical model for detecting diabetes using glucose tolerance tests. The model uses differential equations to represent how glucose and hormone levels in the blood change over time after consuming glucose. It assumes glucose and hormone levels start at equilibrium. The solution shows blood glucose levels will oscillate underdamped for diabetics, reaching abnormal highs and lows. The natural frequency of oscillations can indicate if results are diabetic or non-diabetic.

1. (MA 102)
DETECTION OF DIABETES
MATHS PROJECT
WORK
By:-
Anand Yadav15110015
Anurag Gupta 15110028
Rahul Bharti 15110094
Rishikesh More 15110074

3. DETECTION OF DIABETES
 ABSTRACT:
 Diabetes mellitus is a disease of metabolism
which is characterized by excess of sugar in the
blood and urine.
 In diabetes the body is unable to burn off all its
sugar, starches and carbohydrates due to
insufficient supply of insulin.

4. THEORY:
 Glucose is a source of energy of all tissues and organs.
for each individual there is an optimal blood glucose
concentration. Any excessive deviation from this
concentration leads to diabetes and other pathological
conditions.
 Blood glucose levels are influenced and controlled by a
variety of hormone and metabolism , some hormones are
listed as follows :
 Insulin
 Glucagon
 Thyroxine
Now we would like to introduce some terms regarding the test:

5. In Glucose Tolerance Test (GTT) the subject
fasts for 24 hour
and then he is given a large dose of glucose.
After that he is kept under consideration of
doctor.
The glucose level in his blood is monitored by
taking 5 to 6 observations for next 4 to 5
hour.
An abnormal response indicates Diabetes.

6.  The model postulated is simple one, requiring
only a minimum no. of blood sample during a
GTT, and it centers on two concentrations:
(a) G( glucose in the body)
(b) H(net hormonal concentration)
 A change in G or H will have its own
effect on G and H.
 In other words, this is an ideal
beginning of a deferential equation.

7. Where J(t) is external rate at
which
Blood glucose conc. is
increasing
The model is described by these differential
equations:
We assume that for a 24 hour fasting patient H
and G are at
Equilibrium value H0, G0
F1 = 0 = F2

8. We are interested in deviation from equilibrium value.
For small g and h : -
e1 and e2 are errors and are constants.

9. So, further we got:-
OR
Now it is not correctly possible to determine the exact value of
coefficient,
But by examining physiological mechanisms it is possible to get their
sign.

10.  𝑎 > 0, 𝑠𝑖𝑛𝑐𝑒
𝑑𝑔
𝑑𝑡
< 0 𝑓𝑜𝑟 ℎ = 0, 𝑡ℎ𝑟𝑜𝑢𝑔ℎ 𝑡𝑖𝑠𝑠𝑢𝑒 𝑖𝑛𝑡𝑎𝑘𝑒 𝑜𝑓 𝑔𝑙𝑢𝑐𝑜𝑠𝑒.
 𝑏 > 0, 𝑠𝑖𝑛𝑐𝑒 ℎ > 0 𝑡𝑒𝑛𝑑𝑠 𝑡𝑜 𝑑𝑒𝑐𝑟𝑒𝑎𝑠𝑒 𝑏𝑙𝑜𝑜𝑑 𝑔𝑙𝑢𝑐𝑜𝑠𝑒 𝑙𝑒𝑣𝑒𝑙𝑠.
 𝑐 > 0, 𝑓𝑜𝑟 𝑔 > 0 𝑐𝑎𝑢𝑠𝑒𝑠 𝑡ℎ𝑒 𝑒𝑛𝑑𝑜𝑐𝑟𝑖𝑚𝑒 𝑔𝑙𝑎𝑛𝑑𝑠
𝑡𝑜 𝑠𝑒𝑐𝑟𝑒𝑡 𝑡ℎ𝑜𝑠𝑒 ℎ𝑜𝑟𝑚𝑜𝑛𝑒𝑠 𝑡ℎ𝑎𝑡 𝑡𝑒𝑛𝑑𝑠 𝑡𝑜 𝑖𝑛𝑐𝑟𝑒𝑎𝑠𝑒 ℎ.
 𝑑 > 0, 𝑠𝑖𝑛𝑐𝑒 𝑡ℎ𝑒 𝑐𝑜𝑛𝑐. 𝑜𝑓 ℎ𝑜𝑟𝑚𝑜𝑛𝑒𝑠 𝑖𝑛 𝑏𝑙𝑜𝑜𝑑 𝑑𝑒𝑐𝑟𝑒𝑎𝑠𝑒𝑠
𝑡ℎ𝑟𝑜𝑢𝑔ℎ ℎ𝑜𝑟𝑚𝑜𝑛𝑒 𝑚𝑒𝑡𝑎𝑏𝑜𝑙𝑖𝑠𝑚.
Equation A
Equation B

11. Differentiating Equation A and substituting value of
𝑑ℎ
𝑑𝑡
form equation B.
From equation A substituting h.
Here R(t)= 𝑑𝑗 +
𝑑𝑗
𝑑𝑡
Equation C

12. J~(external rate at which
Glucose conc. Is being increased.)
R(t) is always 0 except when glucose is being ingested in starting of
GTT.
So, equation can be made homogeneous easily.
It has three type solution like an oscillating spring.
 Underdamped
 Critically damped
 Overdamped
In starting we had made some assumption for J.

13. It is found that a diabetic experiences fluctuating blood glucose
levels that rise above and fall below the optimal level.
So, considering physical reality of diabetes an underdamped
solution is more appropriate.

14. So, solution of the for g is: -
Actual total glucose conc.
There are five constants can be found by taking five
observations.

15. Here 𝜔 is natural frequency of the body system and is not
influenced by measurement too much, it is a good
indicator to represent inference of GTT.
𝑇 =
2𝜋
𝜔
T <4 Hours, interprets the subject is non-diabetic.
T>4 Hours, indicates Diabetes.

16. Here some references where we looked for solutions , pictures,
ideas, etc.
References:-
• https://en.wikipedia.org/wiki/Glucose_tolerance_test
• http://129.81.170.14/~xdw/course/224/diabetes.pdf
• https://www.google.co.in/search?q=underdamped+oscillation&
espv=2&biw=1366&bih=667&source=lnms&tbm=isch&sa=X&
ved=0ahUKEwij5_7vqJPMAhULWI4KHftsBmEQ_AUIBigB#tb
m=isch&tbs=rimg%3ACbzYzob92dSUIjhJZzOLomGcyBYe9H
V6Y2eqGOoV8Eq1vqaoaRI8oLpT4r2wNPEZX_1OPQn-
k8SHaZfiNYJ-zBsCufioSCUlnM4uiYZzIEeT0FRaE-
0dbKhIJFh70dXpjZ6oR-0TJcGYftAUqEgkY6hXwSrW-
phGbxUzgxlPBdyoSCahpEjygulPiEQxpSvVNIihvKhIJvbA08Rl
f848RSfc8NzQwAfsqEglCf6TxIdpl-
BH6V_1QP2Isw_1ioSCY1gn7MGwK5-
EWqMVA1CLtAL&q=underdamped%20oscillation&imgrc=SW
czi6JhnMhFRM%3A
• http://home2.fvcc.edu/~dhicketh/DiffEqns/spring13projects/Jo
nAlanProject/Project.pdf