Lenses for the masses - introducing Goggles

LENSES FOR
THE MASSES
…introducin
g Goggles
@KenScambler
λ

class Pos {
var x: Int = _
var y: Int = _
}
class Entity {
var pos: Pos = _
var embubbled: Boolean = _
}
class Game {
var player1, player2: Entity = _
var monsters: ListBuffer[Entity] = _
var bubbles: ListBuffer[Bubble] = _
var score: Int = _
}

“Assignment… leads us into a
thicket of difficult conceptual
issues.”
Ch. 3.1.2

“Nevertheless… it is a powerful
technique for maintaining a
modular design.”
Ch. 3.1.2

• Tracks state over time
• Local change instantly
propagates without external
knowledge or orchestration
• Efficient
• Can’t reason locally
• Can’t substitute expressions
with result
• Spooky action at a distance
• Disadvantages are infectious
• Forget about concurrency
• Hard to isolate things for
testing
• Can’t fit behaviour patterns in
your head
GOOD BAD
Mutable?

case class Pos(x: Int, y: Int)
sealed trait Entity { def pos: Pos }
case class Monster(pos: Pos, embubbled: Boolean)
extends Entity
case class Player(pos: Pos, lives: Int)
extends Entity
case class Bubble(pos: Pos) extends Entity
case class Game(
player1: Player,
player2: Option[Player]
monsters: List[Monster],
bubbles: List[Bubble],
score: Int)

game.copy(player =
game.player.copy(pos =
game.player.pos.copy(x =
game.player.pos.x + 10
)
)
)
218

• Referential transparency
• Local reasoning
• Equational reasoning
• Easily testable
• Need to manually orchestrate
position
• Need to know path
information within world
• Need to know how to recreate
in the world
• Need to write a lot of stuff
• Repetitive, hard to read
• Inefficient
Immutable?
GOOD BAD

Apparently it is terrible at a bunch of
common problems
😳
FP is supposed to be all about modularity!

set: S  A  S
get: S  A
LENS

(X,Y)
e => e.pos
e => p => e.copy(pos = p)
LENS
pos

(X,Y)
p => x
p => x2 => p.copy(x = x2)
LENS
Int
x

208
(playerL ∘ posL ∘ xL).get(game)

218
(playerL ∘ posL ∘ xL).modify(game)(_ + 10)

setBack: A  S
maybeGet: S  S | A
PRISM

{
case m: Player => Right(m)
case e => Left(e)
}
PRISM
asPlayer

monsters each
Lens Traversal
embubbled
Bool
Lens

Traversal
monstersEmbubblement
Bool

(monsters ∘ each ∘ embubbled).getList(game)
false
true
false false
falsefalse
false

Iso
Lens
(X,Y)
×1
×1
Prism
×0-1
Traversal
×0-n

Optics libraries are
too hard to learn
2

data Player = Player { _playerPos :: Pos
, _lives :: Int }
data Pos = Pos { _x :: Int, _y :: Int }
data Monster = Monster { _monsterPos :: Pos
, _embubbled :: Bool }
data Bubble = Bubble { _bubblePos :: Pos }
data Game = Game
{ _player1 :: Player
, _monsters :: [Monster]
, _bubbles :: [Bubble]
, _score :: Int
}
makeLenses ''Player
makeLenses ''Pos
makeLenses ''Monster
makeLenses ''Bubble
makeLenses ''Game

import Control.Lens
g = Game (Player (Pos 33 22) 3)
[ Monster (Pos 1 2) True
, Monster (Pos 44 102) False
] [] 1000
view monsters g

Lens
(1,2) (33,88)(44,102)

import Control.Lens
] [] 1000
toListOf (monsters.each) g

Traversal
(1,2) (33,88)(44,102)

import Control.Lens
] [] 1000
toListOf
(monsters.each.monsterPos) g

Traversal
(1,2) (44,102) (33,88)

import Control.Lens
] [] 1000
toListOf
(monsters.each.monsterPos.x) g

Traversal
1, 44, 33

import Control.Lens
] [] 1000
set
(monsters.each.monsterPos.x)
11 g

(11,2) (11,88)(11,102)

import Control.Lens
] [] 1000
over
(monsters.each.monsterPos.x)
(+1) g

(2,2) (34,88)(45,102)

import Control.Lens
] [] 1000
monsters.each.monsterPos.x .~ 11
$ g

(11,2) (11,88)(11,102)

import Control.Lens
] [] 1000
monsters.each.monsterPos.x %~ (+1)
$ g

(2,2) (34,88)(45,102)

class (
Choice p,
Corepresentable p,
Comonad (Corep p),
Traversable (Corep p),
Strong p,
Representable p,
Monad (Rep p),
MonadFix (Rep p),
Distributive (Rep p),
Costrong p,
ArrowLoop p,
ArrowApply p,
ArrowChoice p,
Closed p) => Conjoined p where ...

Boring problems demand boring
solutions!

Easy solutions are
too limited
3

(def users [{:name "Linda" :age 30}
{:name "Tom" :age 20}])
(get-in users [0 :name])
”Linda”
(update-in users [1 :age] + 1)
 [{:name ”Linda" :age 30}
{:name ”Tom" :age 21}]
(assoc-in users [1 :name] "Sparkles")
 [{:name ”Linda" :age 30}
{:name ”Sparkles" :age 20}])

[{"name": "Linda", "age": 30},
{"name": "Tom", "age": 20}]
.[0].name
“Linda”
.[].age += 1
 [{"name": "Linda", "age": 31},
{"name": "Tom", "age": 21}]
.[1].name |= "Sparkles”
 [{"name": "Linda", "age": 30},
{"name": ”Sparkles", "age": 20}]

<people>
<person>
<name>Linda</name>
<age>30</age>
</person
<person>
<name>Tom</name>
<age>20</age>
</person>
</people>
/people/person[1]/name
 <name>Linda</name>
/people/person/age
 <age>30</age>
<age>20</age>

[1,2,3]*.multiply(2)
[2,4,6]

Solutions that cut
corners don’t scale.

class Lens[S,A]
class Traversal[S,A]
class Prism[S,A]
class Iso[S,A]
class Fold[S,A]
class Getter[S,A]
class Setter[S,A]
class Optional[S,A]

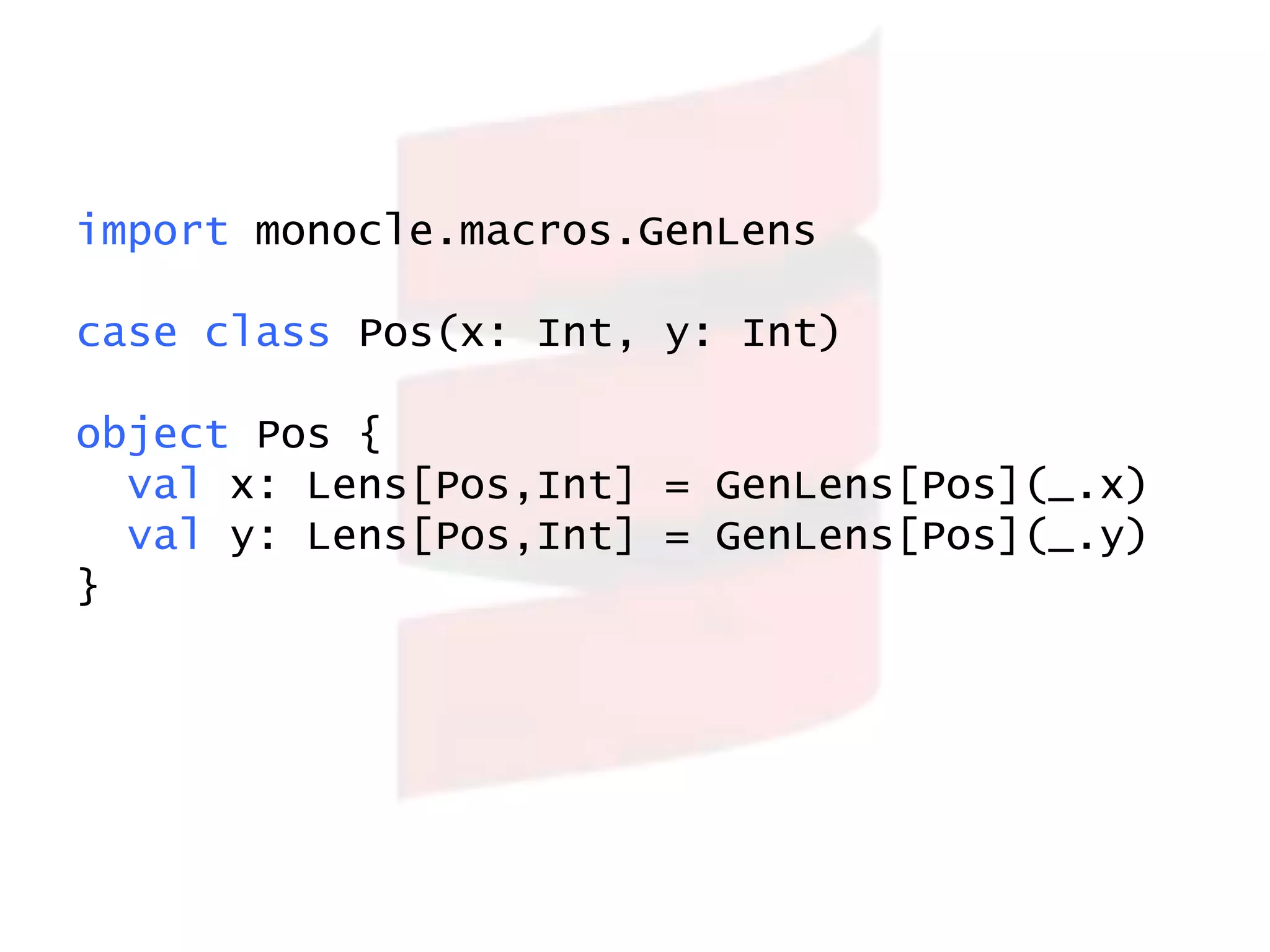
import monocle.macros.GenLens
object Pos {
val x: Lens[Pos,Int] = GenLens[Pos](_.x)
val y: Lens[Pos,Int] = GenLens[Pos](_.y)
}

import monocle.macros.Lenses
@Lenses
@Lenses
case class Monster(pos: Pos,
embubbled: Boolean)
// in build.sbt
addCompilerPlugin(
"org.scalamacros" %% "paradise" %
"2.1.0" cross CrossVersion.full)

Game.monsters.composeTraversal(each).
composeLens(Monster.pos).
composeLens(Pos.x).set(11)(g)

(11,2) (11,88)(11,102)

Goggles
https://github.com/kenbot/goggles

Goggles principles
• You already know how to use it
• Gets out of the way of experts
• Fabulous first-class error messages

Goggles syntax
import goggles._
get"$g.monsters[1].embubbled”
set"$g.monsters*.pos.x" := 55555
set"$g.player2?.lives" ~= (_ + 3)

val g: Game
val posL: Lens[Monster, Pos]
get"${g}.monsters*.${posL}.x"

${game}
".monsters*."
${posL}
".x"
Macro
ERROR
{
or
…
}
Mode = GET
""

".monsters*." ".x"
Hole Name(monsters) Each Hole Name(x)
List[String]
AST
""

trait Parse[T, Arg, A] {
def apply(state: ParseState[T,Arg]):
(Either[GogglesError[T],A],
ParseState[T,Arg])
}
Interpreter monad

(List[Arg], List[Info])
(Either[Error,A], List[Arg], List[Info])
Interpreter monad

${game} ${posL}Args:
Info:
AST:
Tree:
Hole Name(monsters) Each Hole Name(x)

${game}
${posL}Args:
Info:
AST:
Hole
Tree:
”$game", Unit, Game, Iso, Iso
const(game)
Name(monsters) Each Hole Name(x)

Info:
AST:
Tree:
const(game).composeGetter(Getter(_.monsters))
".monsters", Game, List[Monster], Getter, Getter
${posL}Args:
Name(monsters)
Each Hole Name(x)

Info:
AST:
Each
Hole Name(x)
Tree:
.composeTraversal(Each.each)
"*", List[Monster], ??????, Traversal, Fold
${posL}Args:
How to learn the type of values?

Info:
AST:
Each
Hole Name(x)
Tree:
"*", List[Monster], Monster, Traversal, Fold
${posL}Args:
typecheck(
q"implicitly[
_root_.monocle.function.
Each[List[Monster], _]]")
Typechecking will fill it in for us

Info:
AST:
Each
Hole Name(x)
Tree:
${posL}Args:
Got it!

${posL}
Args:
Info:
AST:
Hole
Name(x)
Tree:
.composeLens(posL)
”$posL", Monster, Pos, Lens, Fold

Info:
AST:
Name(x)
Tree:
.composeLens(posL)
.composeGetter(Getter(_.x))
".x", Pos, Int, Getter, Fold

Info:
Error: NameNotFound("BLAH", Int)
".x", Pos, Int, Getter, Fold
get”$g.monsters*.$posL.x.BLAH"

Optics are here to
stay!
• Benefits of immutability
• Benefits of mutation
• Vast abstractive power

Optics are here to
stay!
• Built-in support is really needed for good usability
• Future languages will have built-in optics
• Perhaps Goggles can help inform this process!
Watch this space!

Lenses for the masses - introducing Goggles

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to Lenses for the masses - introducing Goggles

Similar to Lenses for the masses - introducing Goggles (20)

More from kenbot

More from kenbot (12)

Recently uploaded

Recently uploaded (20)

Lenses for the masses - introducing Goggles