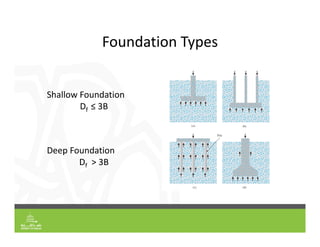
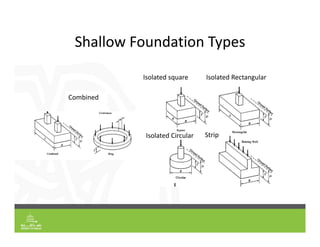
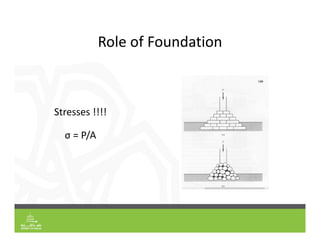
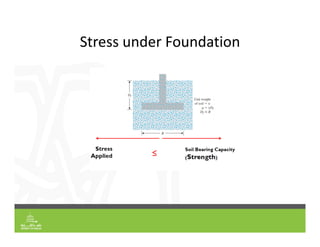
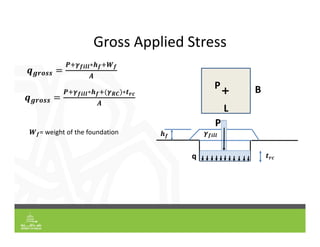
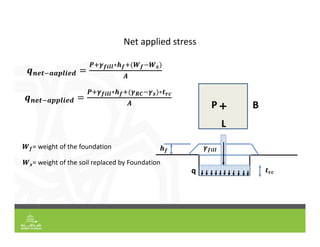
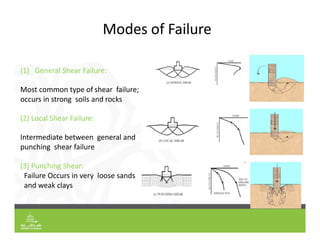
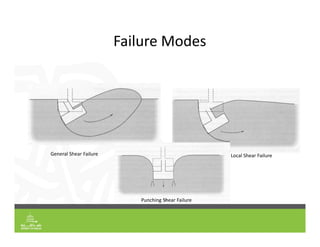
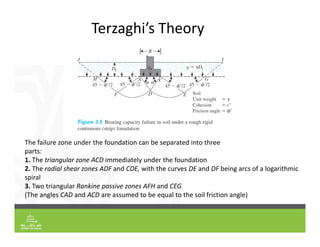
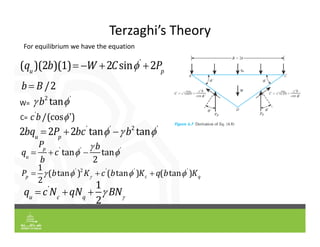
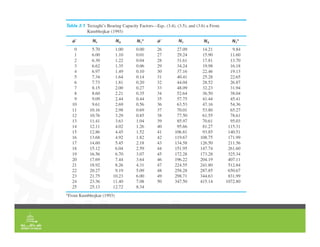
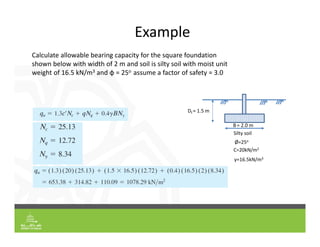
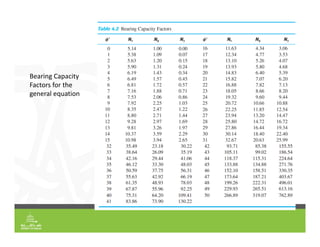
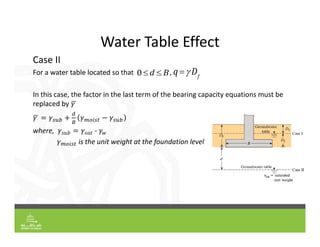
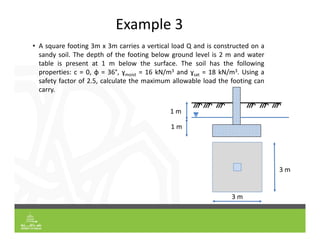
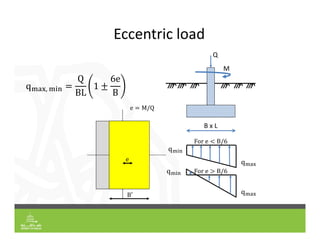
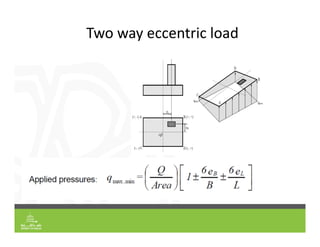
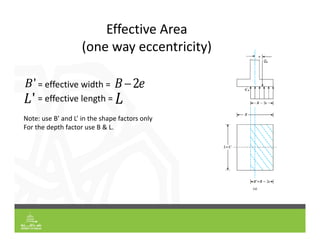
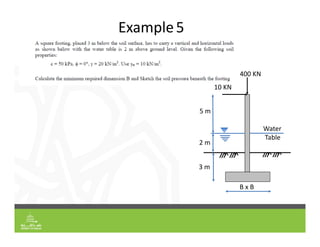
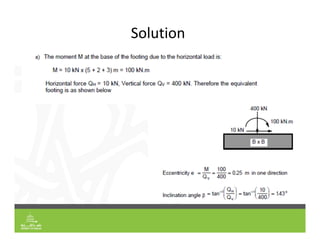
This document provides an overview of shallow foundation types and soil bearing capacity. It discusses the different failure modes of shallow foundations, including general shear, local shear, and punching shear failure. Terzaghi's theory of bearing capacity is explained, including his equations. Factors that affect bearing capacity like foundation shape, depth, load inclination, and water table are also covered. Examples are provided to demonstrate calculating ultimate and allowable bearing capacity using Terzaghi's equations and accounting for factors like eccentric loading.

1. Foundation Engineering
Fall 2020/2021
Soil Bearing Capacity
Mohamed G. Arab, Ph.D.
Assistant Professor
Civil & Environmental Engineering

2. Agenda
 Shallow Foundation Types
 Soil Bearing Capacity Shallow Foundation
 Shallow Foundation Failure Modes
 Shallow Foundation Bearing Capacity Estimation

3. Foundation Types
Shallow Foundation
Df ≤ 3B
Deep Foundation
Df > 3B

4. Shallow Foundation Types
Strip
Isolated square
Combined
Isolated Rectangular
Isolated Circular

5. Role of Foundation
Stresses !!!!
σ = P/A

6. Shallow Foundation

7. Shallow Foundation Construction

8. Stress under Foundation
≤

9. Gross Applied Stress
𝒒𝒈𝒓𝒐𝒔𝒔
𝑷 𝜸𝒇𝒊𝒍𝒍∗𝒉𝒇 𝑾𝒇
𝑨
P
q
P B
L
𝜸𝒇𝒊𝒍𝒍
𝒉𝒇
𝑾𝒇= weight of the foundation
𝒒𝒈𝒓𝒐𝒔𝒔
𝑷 𝜸𝒇𝒊𝒍𝒍∗𝒉𝒇 𝜸𝑹𝑪 ∗𝒕𝒓𝒄
𝑨
𝒕𝒓𝒄

10. Net applied stress
P B
L
q
𝜸𝒇𝒊𝒍𝒍
𝒉𝒇
𝒕𝒓𝒄
𝒒𝒏𝒆𝒕 𝒂𝒂𝒑𝒍𝒊𝒆𝒅
𝑷 𝜸𝒇𝒊𝒍𝒍∗𝒉𝒇 𝑾𝒇 𝑾𝒔
𝑨
𝒒𝒏𝒆𝒕 𝒂𝒑𝒑𝒍𝒊𝒆𝒅
𝑷 𝜸𝒇𝒊𝒍𝒍∗𝒉𝒇 𝜸𝑹𝑪 𝜸𝒔 ∗𝒕𝒓𝒄
𝑨
𝑾𝒇= weight of the foundation
𝑾𝒔= weight of the soil replaced by Foundation

11. Modes of Failure
(1) General Shear Failure:
Most common type of shear failure;
occurs in strong soils and rocks
(2) Local Shear Failure:
Intermediate between general and
punching shear failure
(3) Punching Shear:
Failure Occurs in very loose sands
and weak clays

12. Failure Modes
General Shear Failure Local Shear Failure
Punching Shear Failure

13. Failure Modes
General Shear Failure
on low compressibility (dense or stiff) soils
heaving on both sides of foundation
Tilting of structure
Local Shear Failure
on highly compressible soils
No Tilting of structure, Slight heaving
Punching Shear Failure
on loose, uncompacted soils
No Tilting of structure or heaving

14. Terzaghi’s Theory
Terzaghi’s assumptions
• L/B ratio is large = plain strain problem
• Shear resistance of soil for Df depth is neglected
• General shear failure Shear strength is governed by Mohr‐Coulomb Criterion

15. Terzaghi’s Theory
The failure zone under the foundation can be separated into three
parts:
1. The triangular zone ACD immediately under the foundation
2. The radial shear zones ADF and CDE, with the curves DE and DF being arcs of a logarithmic
spiral
3. Two triangular Rankine passive zones AFH and CEG
(The angles CAD and ACD are assumed to be equal to the soil friction angle)

16. Terzaghi’s Theory
For equilibrium we have the equation
(qu
)(2b)(1) W 2Csin'
2Pp
b  B /2
 b2
tan'
W=
c'
b/(cos')
C=
2bqu
2Pp
2bc'
tan'
 b2
tan'
' 2 ' ' '
1
( tan ) ( tan ) ( tan )
2

   
  
p c q
P b K c b K q b K
qu
 c'
Nc
qNq

1
2
 BN
qu

Pp
b
c'
tan'

 b
2
tan'

17. Terzaghi’s Equation
Nc
 tan'
(Kc
1)
Nq
 Kq
tan'
N

1
2
tan'
(K
tan'
1)
Nq
 tan2
(45
'
2
)e tan'
Nc
(Nq
1)cot'
N
 2(Nq
1)tan'

19. Terzaghi’s Equation
 To estimate the ultimate bearing capacity of square and circular
foundations, use the following equations.
Square foundation
Circular foundation
qu
1.3c'
Nc
qNq
0.4 BN
qu
1.3c'
Nc
qNq
0.3 BN

20. Allowable Bearing Capacity
• Net ultimate bearing capacity: The ultimate pressure per unit area of the foundation
that can be supported by the soil in excess of the pressure caused by the
surrounding soil at the foundation level.
• If the difference between the unit weight of concrete used in the foundation and
the unit weight of soil surrounding is assumed to be negligible, then
= net ultimate bearing capacity
So (here the factor of safety should be at least 3)
qnet(u)
 qu
q
qnet(u)
q  Df
qall(net )

qu
q
FS

21. Example
Ø=25o
Silty soil
Df = 1.5 m
C=20kN/m2
γ=16.5kN/m3
Calculate allowable bearing capacity for the square foundation
shown below with width of 2 m and soil is silty soil with moist unit
weight of 16.5 kN/m3 and φ = 25o assume a factor of safety = 3.0
B= 2.0 m

22. Solution
un u
2
all net
qun
FS
=
1053.34
3
= 351.18 2

23.  To account for all those shortcomings, Meyerhof suggested the following equation:
c‘ = cohesion
q = effective stress at the lever of the bottom of the foundation
γ = unit weight of soil
B = width of foundation (= diameter for a circular foundation)
 = shape factors

 = depth factors

 = load inclination factors
 = bearing capacity factors
General Equation, Meyerhof (1963)
qu
 c'
Nc
Fcs
Fcd
Fci
qNq
Fqs
Fqd
Fqi

1
2
 BN
F s
F d
F i
Fcs
,Fqs
,F s
Fcd
,Fqd
,F d
Fci
,Fqi
,F i
Nc
,Nq
,N

24. Shape Factors
q cN F qN F 0.5γBN F
Where:
• F 1
• F 1 tan∅
• F 1 0.4
Note:
Square footing: B = L
Circular footing: B = L = D
Strip footing: L  
Where B = Smallest dimension
L = Largest dimension

25. Depth Factors
Df/B ≤ 1 Df/B > 1
F 1 0.4
D
B
F 1 2 tan∅ 1 sin∅
D
B
F 1
F 1 0.4 tan
D
B
F 1 2 tan∅ 1 sin∅ tan
D
B
F 1
Where tan is in radians

26. Inclination Factors
β

27. Bearing Capacity
Factors for the
general equation

28. Water Table Effect
Case I
If the water table is located so that , the factor
in the bearing capacity equations takes the form:
= effective surcharge =
= saturated unit weight of soil, = unit weight of water
0 D1
 Df
q D1
 D2
( sat
 w
)
 sat  w

29. Water Table Effect
 Case II
 For a water table located so that ,
 In this case, the factor in the last term of the bearing capacity equations must be
replaced by 𝛾
 𝛾 𝛾 𝛾 𝛾
 where, 𝛾𝑠𝑢𝑏 𝛾𝑠𝑎𝑡 ‐ 𝛾𝑤
𝛾 is the unit weight at the foundation level
0 d  B q Df

32. Example 3
• A square footing 3m x 3m carries a vertical load Q and is constructed on a
sandy soil. The depth of the footing below ground level is 2 m and water
table is present at 1 m below the surface. The soil has the following
properties: c = 0, φ = 36°, ɣmoist = 16 kN/m3 and ɣsat = 18 kN/m3. Using a
safety factor of 2.5, calculate the maximum allowable load the footing can
carry.
1 m
1 m
3 m
3 m

33. Solution
With c= 0, the ultimate bearing capacity equation is reduced to
q qN F F +0.5γBN F F
Bearing capacity factors:
Using ∅ 36°
,
N tan 45 36/2 e =37.7
N 2 37.7 1 𝑡𝑎𝑛36 56.3
Shape Factors:
F 1 1/1 tan 36 = 1.73
F 1 0.4 = 0.6
Depth Factors
With Df/B = 2/3 < 1 then
F 1 2 tan 36 1 sin36 =1.16
F 1
Also
𝛾 𝛾 ‐𝛾 = 18‐9.81 = 8.2 kN/m3
The effective stress, q, at the bottom of the footing is
q = 1 x 16 + 1 x 8.2 = 24.20 kPa
Substituting these values in B.C eq. we get
qu= 24.2 x 37.7 x 1.73 x 1.16 + (1/2) x 8.2 x 3 x 56.3 x 0.6 = 2246.39 kPa

34. Solution Cont’
q
. .
.
= 888.87 kN/m2
Q q ∗ A = 888.87 x (3x3) = 8000 kN = 80 t

35. Example 4
• Calculate the minimum required dimensions of square footing that has to
carry a concentric allowable load of 400 Tons. The footing is to be placed at
a depth of 3 m below ground level. The soil has the following properties: c =
115 kPa, φ = 15o and ɣ = 18 kN/m3. No water table is present. Use a safety
factor of 3.5
3 m
B x B
400 ton

36. Solution

37. Solution cont’



















1
)
(
B
0.88
+
B
7)
(3.94)(1.2
(18x3)
+
B
1.2
+
B
(1.36)
115(10.98)
=
q net
u
(0.6)(1.0)
.65
0.5B(18)(2
+ )
qunet = c Nc Fcs Fcd + q (Nq Fqs Fqd -1)+ 0.5 γ B Nγ Fγs Fγd
0
=
9
-
B
1
+
B
13
+
B
2
3
33
.
78
8
.
56
9
.
8
2
2
)
(
4000
B
kN
B
Q
A
Q
q net
applied 


)
(
)
( net
all
net
applied q
q 
m
B 1
.
2

min dim. qapplied(net)= qall(net)

38. Eccentric load
q ,
Q
BL
1
6e
B
B x L
Q
M
q
q
For e B/6
q
q For e B/6
Q
e
e M/Q
B′

39. Two way eccentric load

40. Effective Area
(one way eccentricity)
= effective width =
= effective length =
B 2e
L' L
B'
Note: use B’ and L’ in the shape factors only
For the depth factor use B & L.

41. Example5
Water
Table
400 KN
10 KN
5 m
2 m
3 m
B x B

42. Solution

43. Solution

44. Solution

45. Solution

46. Thank you
46
Mohamed G. Arab, Ph.D.
Assistant Professor,
Engineering College, Civil & Environmental Engineering Dept.