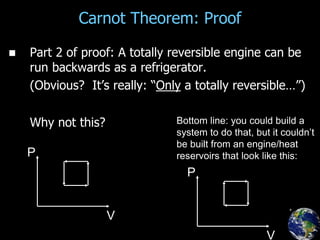
The document discusses various thermodynamic cycles and engines, including: 1. A discussion of reversible vs irreversible processes and examples of each. 2. An explanation of the Carnot cycle and the Carnot theorem, which establishes the maximum possible efficiency for any heat engine or refrigerator. 3. Descriptions of the Brayton cycle and improvements to it using regeneration to approach the efficiency of the Carnot cycle.

1.  Prayer
 Remote Desktop check
 Exam starts a week from tomorrow
a. Avoid Oct 1 and Oct 3 if possible
 Results of doodle.com voting:
a. Exam review will be Wed 5-6:30, room to be
announced
Announcements – 9/21/12
Pearls
Before
Swine

2. From warmup
 Extra time on?
a. Example of a near-perfect Carnot engine; especially
if a video of one exists (sped up, of course), or if
we could see a demo of a Carnot engine in class.
 Other comments?
a. I really don't get irreversibility. Can't you
adiabatically compress and then immediately
decompress a gas? If it's insulated well enough,
don't you get nearly all the energy back?

3. Worked Problem from last time
 Game plan:
a.Find unknown state variables
b.Find Q for each leg
c.Find |Wnet|
d.Then e = |Wnet|/Qh
1, 320K
2
3, 320 K
P
V
202000 Pa
303000 Pa
V2=?
T2=?
0.001 m3
Qc
Qh Qh

4. Demos
 Stirling engine
 Thermoelectric engine

5. Review:
 Second Law
a. Kelvin-Plank
b. new: “Clausius statement”

6. Refrigerators (or air conditioners)
 COPrefrigerator: How good is your refrigerator?
fridge
heat, Qc
work
exhaust, Qh

7. From warmup
 Why would you want to use a heat pump
(instead of an electric heater) to heat your
house when 100% of the energy in an electric
heater can be converted directly to heat? Isn't
that more efficient? Explain.
a. No, because a heat pump is usually around
400% effective. That is, you get 4 times
more energy (in the form of heat) out than
you put in (in the form of work). Because it
pulls energy from the air surrounding it,
instead of just relying on the work that you
put into it.

8. Heat Pumps
 COPheat pump: How good is your heat pump?
heat
pump
heat, Qc
work
“exhaust”, Qh

9. “Reversible” vs. “Irreversible”
 “In order for a process to be [totally*] reversible, we
must return the gas to its original state without
changing the surroundings.”
 Warmup: Give an example of a process that would be
considered reversible if not for that qualifier
a. Yesterday at the physics social we froze things in
liquid nitrogen. When a balloon went in, it
compressed greatly. Then, when it was taken out,
its volume expanded back to its original state.
*Other terminology: internally reversible vs totally reversible.

10. “Reversible” vs. “Irreversible”
a. (My answer) Pretty much any
line that you can draw on a PV
diagram would be reversible if
not for that condition. Consider
a constant volume change, a
vertical line on a PV diagram. If
the surroundings are hot, the
gas will move up the line
towards higher temperature.
By making the surroundings
cold, the gas will move down
the exact same line, reversing
its path.
P
V
state A; TA = 300K
state B; TB = 650K
 Warmup: Give an example of a process that would be
considered reversible if not for that qualifier

11. From warmup
 The Carnot engine is completely impractical… Why
then do we bother? What is important about this
engine?
a. It is important as a standard to measure the
efficiency of other, more practical engines, and
also as a measure of what is possible for
humankind to achieve.
 Why doesn't the Carnot engine have perfect
efficiency?
a. Because no engine can have 100% efficiency
b. Because that would require a cold reservoir at 0K,
which is impossible.

12. Carnot Cycle
 All heat added/subtracted
reversibly
a. During constant
temperature processes
b. Drawback: isothermal =
slow, typically
HW 11-5 – 11-7: find efficiency for a specific Carnot cycle
Optional HW: eC derived for a general Carnot cycle
max
" " 1 c
C
h
T
e e
T
  
“C” for “Carnot”

13. Carnot Theorem
 Second Law, Kelvin-Plank statement
a. You can’t fully convert heat to work
b. You can’t have an efficiency of 100%
 Carnot Theorem:
a. You can’t even have that!
max 1 c
C
h
T
e e
T
  
Th = max temp of cycle
Tc = min temp of cycle

14. Carnot Theorem: How to remember
 Engine: emax = ?
 Refrigerator: COPr,max = ?
 Heat pump: COPhp,max = ?

15. Carnot Theorem: Proof
 Part 1 of proof: The Kelvin-Plank statement of the Second
Law is equivalent to the Clausius statement.
Clausius: Heat energy does not spontaneously flow from cold
to hot.
Kelvin-Plank: You can’t fully convert all heat to work.
What if you could make heat go from coldhot?
What if you could make a perfect engine? Then use it to
power a refrigerator.
engine
heat
work
exhaust
Then do this:

16. Carnot Theorem: Proof
 Part 2 of proof: A totally reversible engine can be
run backwards as a refrigerator.
(Obvious? It’s really: “Only a totally reversible…”)
Why not this?
P
V
Bottom line: you could build a
system to do that, but it couldn’t
be built from an engine/heat
reservoirs that look like this:
P
V

17. Carnot Theorem: Proof
 Part 3 of proof: Suppose you had an engine with
e > emax. Then build a Carnot engine using the
same reservoirs, running in reverse (as a fridge).
Use the fridge’s heat output to power the engine:
Which work is bigger? Can you see the problem?
fridge
Qc
work
Qh engine
work
exhaust
(at Tc)

18. Multi-Stage Carnot Engine?
 Build a new cycle using only isotherms and
adiabats.
 Result?

19. “Regeneration”
 Any engineers in the crowd?
 The other way that you can transfer heat without
changing entropy: internal heat transfer
 The Brayton cycle: Used by most non-steam
power plants
Isothermal contour

20. Brayton cycle, cont.
 What does temperature look like at each point?
 Use “T-S” diagram. “S” = entropy, we’ll talk much more
about on Monday
 For now, just know that adiabatic = constant S.
 Focus on y-axis
Look here!

21. Brayton cycle with regeneration
 Add another compressor & another turbine to increase
the range over which regeneration can be done
 With an infinite number of compressors/turbines, you get
the Carnot efficiency! (even with const. pressure
sections)
Image from http://web.me.unr.edu/me372/Spring2001/The%20Brayton%20Cycle%20with%20Regeneration.pdf
(who apparently got it from a textbook, but I’m not sure which one)