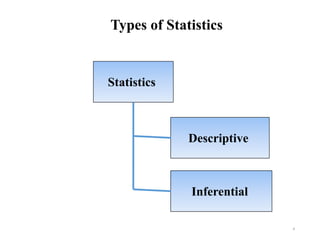
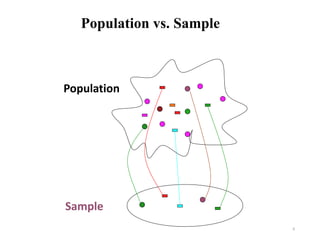
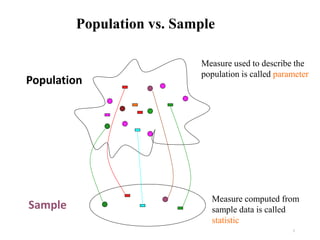
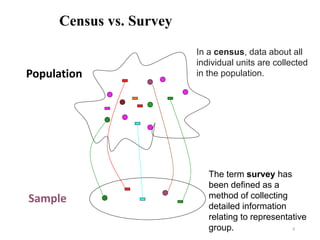
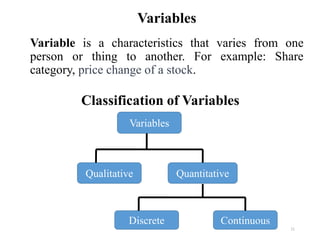
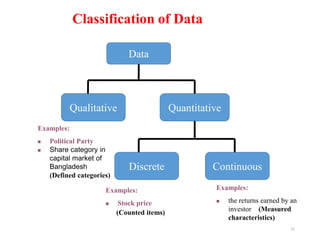
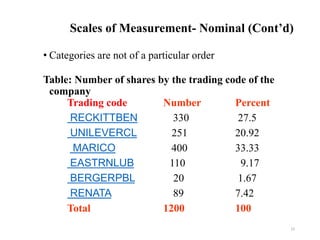
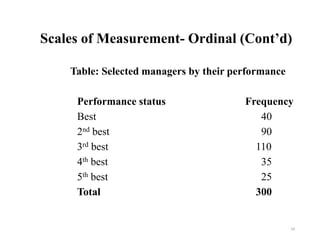
This document provides an introduction to statistics. It defines statistics as the science of assembling, classifying, tabulating and analyzing data to make generalizations and decisions. Many fields use statistics, including economics, social science, business, politics, psychology and more. The document outlines descriptive and inferential statistics, and defines key statistical concepts such as populations, samples, parameters, statistics, variables, data types, and scales of measurement including nominal, ordinal, interval and ratio scales.

1. Introduction to Statistics
Dr. Tamanna Islam
Bangladesh Institute of Capital Market (BICM)
1

2. What is Meant by Statistics?
Statistics is the science of assembling,
classifying, tabulating and analyzing data for
the purpose of making generalizations and
decisions.
2

3. Who Uses Statistics?
3
Few fields or disciplines where statistical application
is indispensable are given in the following
Economics
Social science
Business
Politics
Psychology
Computer science
Medicine
Genetics
Epidemiology
Environmental studies
Geology
Geography

4. Statistics
Descriptive
Inferential
Types of Statistics
4

5. Types of Statistics
• Descriptive Statistics: Methods of organizing,
summarizing, and presenting data in an informative way.
• Inferential statistics: The following concepts would be
required for defining inferential statistics.
 A population is a collection of all possible
individuals, objects, or measurements of interest. A
parameter is a summary measure that describes a
characteristic of the population.
 A sample is a representative portion or part of the
population of interest. A statistic is a summary
measure computed from a sample.
5

6. Population vs. Sample
6
Population
Sample

7. Population vs. Sample
7
Population
Sample
Measure used to describe the
population is called parameter
Measure computed from
sample data is called
statistic

8. Census vs. Survey
8
Population
Sample
In a census, data about all
individual units are collected
in the population.
The term survey has
been defined as a
method of collecting
detailed information
relating to representative
group.

9. Descriptive Statistics
•Collect data
• e.g. Survey
•Present data
• e.g. Tables and graphs
•Characterize data
• e.g. Sample mean =
9
i
X
n

Types of Statistics

10. Inferential Statistics
• Estimation
• making estimates about
populations
• Hypothesis testing
• testing hypotheses to draw
conclusions about populations
10
Drawing conclusions and/or making decisions concerning a
population based on sample results.

11. Variables
Variable is a characteristics that varies from one
person or thing to another. For example: Share
category, price change of a stock.
11
Variables
Qualitative Quantitative
Discrete Continuous
Classification of Variables

12. Types of Variables
12
Qualitative Variable
A non-numerically valued variable is called a
qualitative variable or categorical variable.
Example : Share category in capital market of
Bangladesh are qualitative variables.
Quantitative Variable
A numerically valued variable is called a quantitative
variable.
Example: Number of share trade in DSE is a
quantitative variables.

13. Types of Variables (Cont’d)
Quantitative variables can be classified as either discrete
or continuous.
• Discrete variables: can only assume certain values and
there are usually “gaps” between values. For example,
number of coupon payments for a corporate bond.
• Continuous variables: can assume any value within a
specific range. For example, the returns earned by an
investor, cash dividends per share paid by a company .
13

14. Data
Information obtained by observing values of a
variable is data.
14

15. Data
Qualitative Quantitative
Discrete Continuous
Classification of Data
Examples:
 Political Party
 Share category in
capital market of
Bangladesh
(Defined categories)
Examples:
 Stock price
(Counted items)
Examples:
 the returns earned by an
investor (Measured
characteristics)
15

16. Qualitative Data
Data obtained by observing values of a qualitative
variable.
Example: Share category in capital market of Bangladesh
as A, B, G, N, Z. The data received when you are told
Individual’s type is qualitative data.
Quantitative Data
Data obtained by observing values of a quantitative
variable.
Example: Daily sales recorded in DSE will give
quantitative data.
16

17. Discrete Data: Data obtained by observing values of a
discrete variable.
Example: The number of buy and sell in DSE is recorded
for 12 day. The resulting data set is
│3 │0 │4 │3 │1 │0 │6 │2
│0 │0 │1 │2
Possible values for the number of buy and sell are
0,1,2,3, …; these are isolated points on the number line,
so we have a sample consisting of discrete numerical
data.
17

18. Continuous Data: Data obtained by observing values of a
continuous variable.
Example: A sample of 20 investors return earned (hundred
TK) is determined for each one. The resulting data set is:
29.8 27.6 28.3 28.7 27.9 29.9 30.1 28.0 28.7
27.9 28.5 29.5 27.2 26.9 28.4 27.9 28.0 30.0
29.1 26.4
Here we have a sample consisting of continuous data.
18

19. Scales of Measurement
• Measurement is a process of assigning numbers to
some characteristics or variables or events according to
scientific rules.
• Arithmetic and statistical operations for summarizing
and presenting data depend on the levels of
measurement.
 Example- Average height of Bangladeshi male,
Proportion of smokers in a community.
19

20. Scales of Measurement (Cont’d)
Four scales of measurement:
 Nominal scale
 Ordinal scale
 Interval scale
 Ratio scale
20

21. Scales of Measurement- Nominal (Cont’d)
• Nominal scale: The measurement scale, in which
numbers are assigned to the categories or variable values
for identification only, is called a nominal scale.
• For example- name of company’s.
• Each value is a category and the values itself serves
merely as a label on name for the category.
• No assumption of ordering or distance between
categories is made.
21

22. • Categories are not of a particular order
Table: Number of shares by the trading code of the
company
Trading code Number Percent
RECKITTBEN 330 27.5
UNILEVERCL 251 20.92
MARICO 400 33.33
EASTRNLUB 110 9.17
BERGERPBL 20 1.67
RENATA 89 7.42
Total 1200 100
22
Scales of Measurement- Nominal (Cont’d)

23. Scales of Measurement- Ordinal (Cont’d)
Ordinal scale: The measurement scale, in which
numbers are assigned to the categories or
variable values for identification as well as
ranking.
Example: Rank of the managers of mutual funds
based on their performance.
23

24. Scales of Measurement- Ordinal (Cont’d)
Table: Selected managers by their performance
Performance status Frequency
Best 40
2nd best 90
3rd best 110
4th best 35
5th best 25
Total 300
24

25. Scales of Measurement- Interval (Cont’d)
• Interval scale: In this measurement scale, numbers are
assigned to the variable values in such a way that the
level of measurement is broken down on a scale of equal
units and the zero value on the scale is not absolutely
zero.
• For example- The variable temperature can have values
0˚c, 10˚ c, 20˚c etc. Here the value 0˚c does not mean the
absence of temperature. Thus, the value zero in interval
scale is not absolutely zero.
25

26. Scales of Measurement- Ratio (Cont’d)
Ratio scale: The measurement scale, in which numbers
are assigned to the variable values in such a way that the
level of measurement is broken down on a scale of equal
units and the zero value on the scale is absolutely zero.
Example: Rate of return on the investment.
26

27. 27
Exercise
1. Credit ratings for bond issues
2. Cash dividends per share
3. Hedge fund classification types
4. Bond maturity in years

28. Thank You!
28