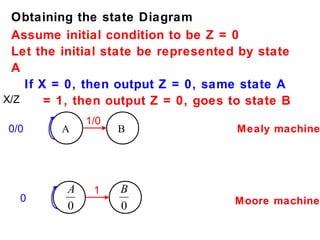
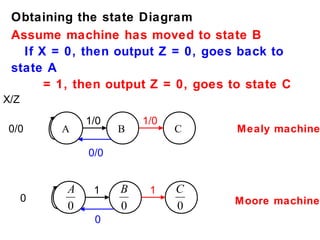
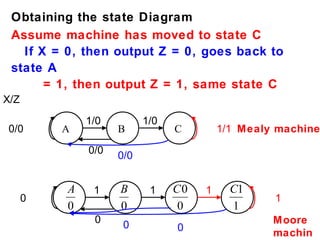
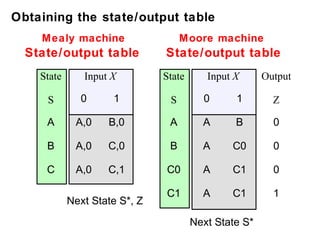
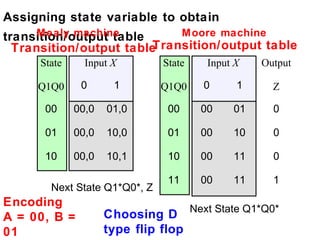
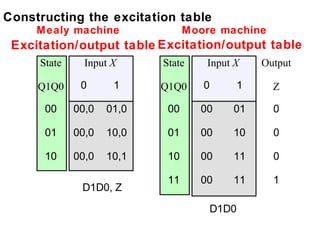
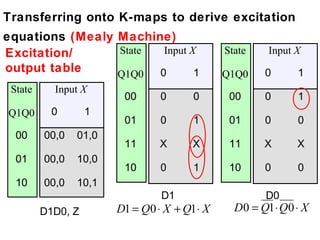
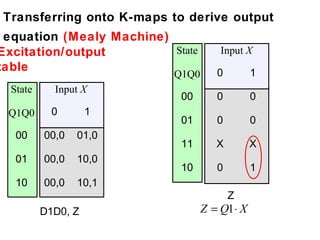
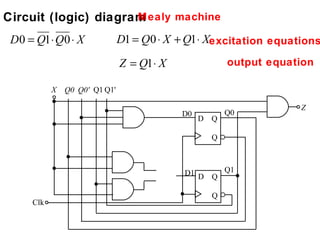
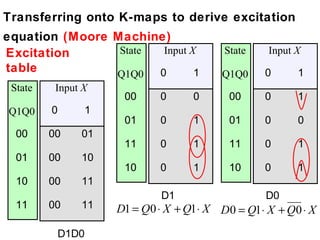
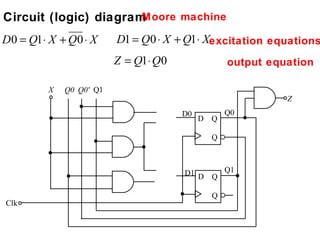
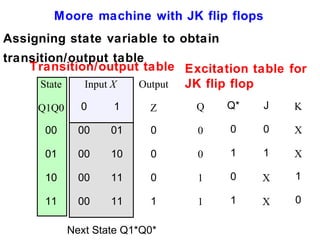
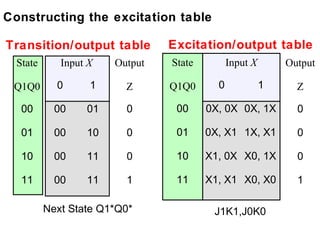
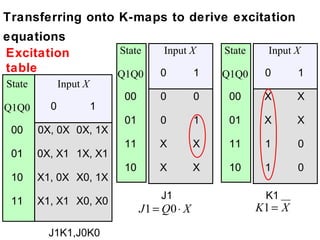
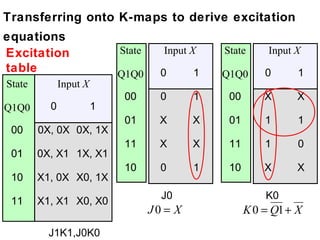
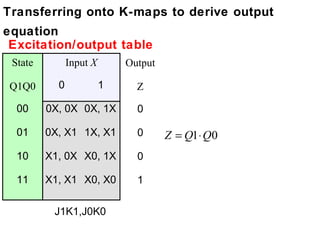
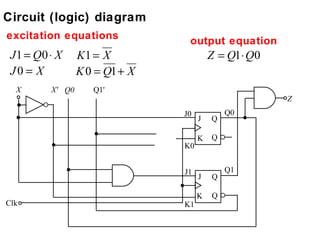
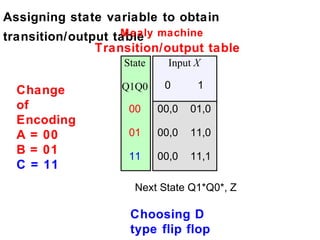
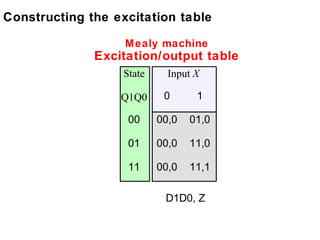
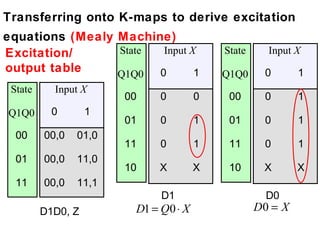
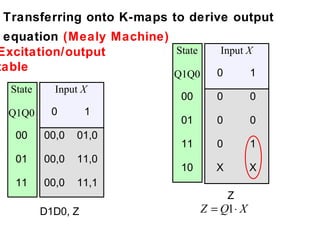
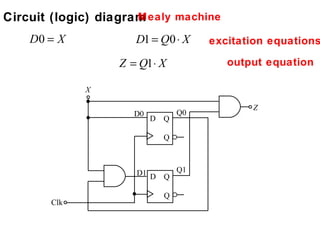
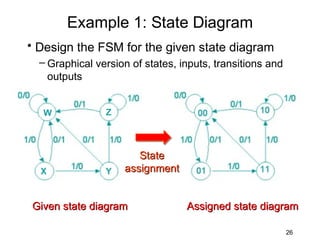
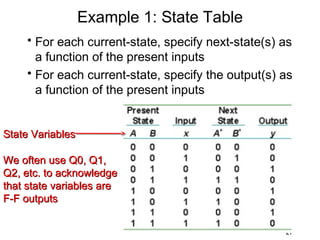
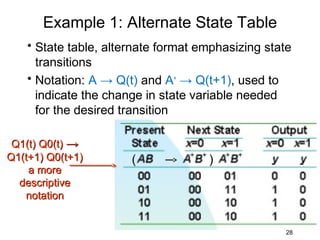
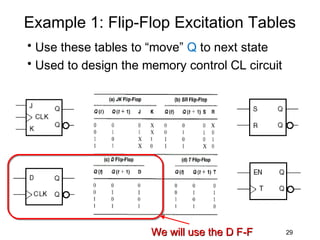
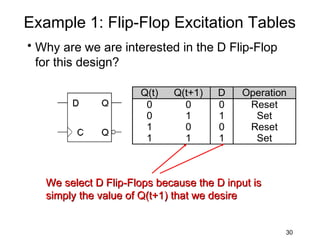
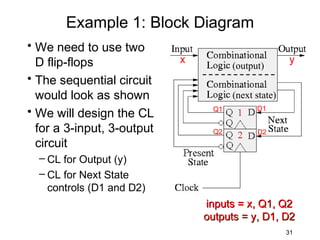
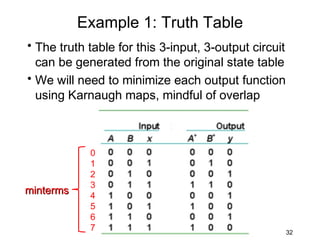
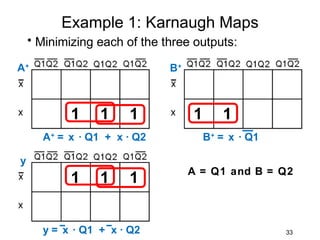
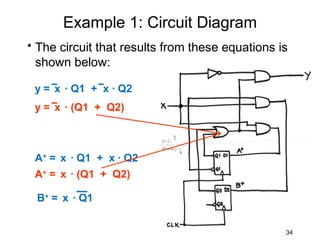
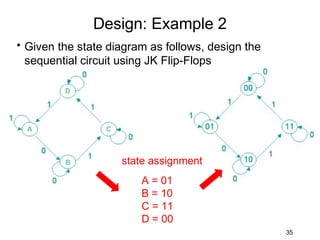
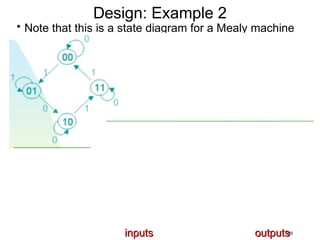
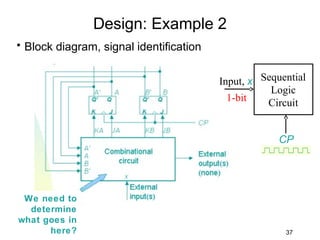
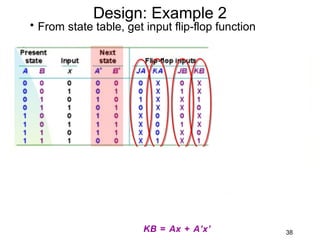
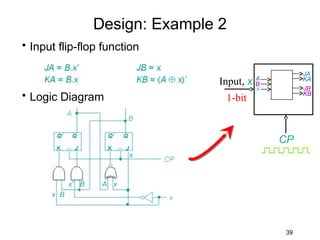
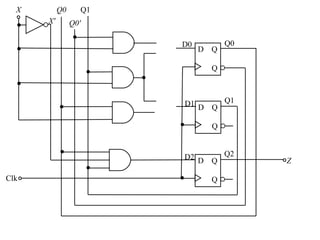
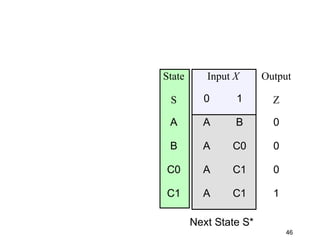
This document describes the process for designing a synchronous state machine using both Mealy and Moore machine approaches. The steps include constructing a state diagram and table, assigning state variables, deriving excitation and output equations, and implementing the design using D or JK flip-flops. An example 3-state machine is designed to detect 3 or more consecutive 1's in an input signal. The example walks through obtaining the state diagram and table, assigning states, and deriving the logic equations for both Mealy and Moore machine implementations.

1. Synchronous Design Process
1. Construct a state diagram and/or state/output
table corresponding to the word description or
specification
2. Minimize the number of states
3. Choose a set of state variables and assign
state variable combinations to the named
states
4. Obtain the transition/output table
5. Determine the number of flip-flops and select
the type of flip-flop to be used (D is often the
default)
6. Construct the excitation table
7. Derive excitation equations
8. Derive output equations 1

2. Design a clocked synchronous state machine
which detects a sequence of three or more
consecutive 1’s in a string of bits coming
through an input line.
Mealy machine with D flip flops
Moore machine with D flip flops
Moore machine with JK flip flops
ealy machine with D flip flops (change of encoding
Assuming Mealy machine design
Let the input be X and output be Z

3. Obtaining the state Diagram
Assume initial condition to be Z = 0
Let the initial state be represented by state
A
If X = 0, then output Z = 0, same state A
X/Z = 1, then output Z = 0, goes to state B
1/0
0/0 A B Mealy machine
A 1 B
0 Moore machine
0 0

4. Obtaining the state Diagram
Assume machine has moved to state B
If X = 0, then output Z = 0, goes back to
state A
= 1, then output Z = 0, goes to state C
X/Z
1/0 1/0
0/0 A B C Mealy machine
0/0
A 1 B 1 C
0 Moore machine
0 0 0
0

5. Obtaining the state Diagram
Assume machine has moved to state C
If X = 0, then output Z = 0, goes back to
state A
= 1, then output Z = 1, same state C
X/Z
1/0 1/0
0/0 A B C 1/1 Mealy machine
0/0 0/0
A 1 B 1 C0 1 C1
0 1
0 0 0 1
0 Moore
0 0 machin

6. Obtaining the state/output table
Mealy machine Moore machine
State/output table State/output table
State Input X State Input X Output
S 0 1 S 0 1 Z
A A,0 B,0 A A B 0
B A,0 C,0 B A C0 0
C A,0 C,1 C0 A C1 0
C1 A C1 1
Next State S*, Z
Next State S*

7. Assigning state variable to obtain
Mealy machine
transition/output table Moore machine
Transition/output table
Transition/output table
State Input X State Input X Output
Q1Q0 0 1 Q1Q0 0 1 Z
00 00,0 01,0 00 00 01 0
01 00,0 10,0 01 00 10 0
10 00,0 10,1 10 00 11 0
11 00 11 1
Next State Q1*Q0*, Z
Encoding
A = 00, B = Choosing D Next State Q1*Q0*
01 type flip flop

8. Constructing the excitation table
Mealy machine Moore machine
Excitation/output table Excitation/output table
State Input X State Input X Output
Q1Q0 0 1 Q1Q0 0 1 Z
00 00,0 01,0 00 00 01 0
01 00,0 10,0 01 00 10 0
10 00,0 10,1 10 00 11 0
11 00 11 1
D1D0, Z
D1D0

9. Transferring onto K-maps to derive excitation
equations (Mealy Machine)
Excitation/ State Input X State Input X
output table Q1Q0 0 1 Q1Q0 0 1
State Input X
00 0 0 00 0 1
Q1Q0 0 1
01 0 1 01 0 0
00 00,0 01,0
11 X X 11 X X
01 00,0 10,0
10 0 1 10 0 0
10 00,0 10,1
D1 D0
D1D0, Z D1 = Q0 ⋅ X + Q1⋅ X D 0 = Q1 ⋅ Q 0 ⋅ X

10. Transferring onto K-maps to derive output
equation (Mealy Machine)
Excitation/output State Input X
table
Q1Q0 0 1
State Input X
00 0 0
Q1Q0 0 1
01 0 0
00 00,0 01,0
11 X X
01 00,0 10,0
10 0 1
10 00,0 10,1
Z
D1D0, Z Z = Q1 ⋅ X

11. Circuit (logic) diagram
Mealy machine
D 0 = Q1 ⋅ Q 0 ⋅ X D1 = Q0 ⋅ X + Q1⋅ Xexcitation equations
Z = Q1 ⋅ X output equation
X Q0 Q0' Q1 Q1'
Z
D0 Q0
D Q
Q
D1 D Q Q1
Q
Clk

12. Transferring onto K-maps to derive excitation
equation (Moore Machine)
Excitation State Input X State Input X
table Q1Q0 0 1 Q1Q0 0 1
State Input X
00 0 0 00 0 1
Q1Q0 0 1
01 0 1 01 0 0
00 00 01
11 0 1 11 0 1
01 00 10
10 0 1 10 0 1
10 00 11
D1 D0
11 00 11 D1 = Q0 ⋅ X + Q1⋅ X D 0 = Q1 ⋅ X + Q 0 ⋅ X
D1D0

13. Transferring onto K-maps to derive output
equation (Moore Machine)
Excitation/output
table
State Input X Output
Q1Q0 0 1 Z
00 00 01 0
01 00 10 0 Z = Q1⋅ Q0
10 00 11 0
11 00 11 1
D1D0

14. Circuit (logic) diagramMoore machine
D 0 = Q1 ⋅ X + Q 0 ⋅ X D1 = Q0 ⋅ X + Q1⋅ Xexcitation equations
Z = Q1⋅ Q0 output equation
X Q0 Q0' Q1
Z
D0 Q0
D Q
Q
D1 D Q Q1
Q
Clk

15. Moore machine with JK flip flops
Assigning state variable to obtain
transition/output table
Transition/output table Excitation table for
State Input X Output JK flip flop
Q1Q0 0 1 Z Q Q* J K
00 00 01 0 0 0 0 X
01 00 10 0 0 1 1 X
10 00 11 0 1 0 X 1
11 00 11 1 1 1 X 0
Next State Q1*Q0*

16. Constructing the excitation table
Transition/output table Excitation/output table
State Input X Output State Input X Output
Q1Q0 0 1 Z Q1Q0 0 1 Z
00 00 01 0 00 0X, 0X 0X, 1X 0
01 00 10 0 01 0X, X1 1X, X1 0
10 00 11 0 10 X1, 0X X0, 1X 0
11 00 11 1 11 X1, X1 X0, X0 1
Next State Q1*Q0* J1K1,J0K0

17. Transferring onto K-maps to derive excitation
equations
Excitation State Input X State Input X
table Q1Q0 0 1 Q1Q0 0 1
State Input X
00 0 0 00 X X
Q1Q0 0 1
01 0 1 01 X X
00 0X, 0X 0X, 1X
11 X X 11 1 0
01 0X, X1 1X, X1
10 X X 10 1 0
10 X1, 0X X0, 1X
J1 K1
11 X1, X1 X0, X0
J 1 = Q0 ⋅ X K1 = X
J1K1,J0K0

18. Transferring onto K-maps to derive excitation
equations
Excitation State Input X State Input X
table Q1Q0 0 1 Q1Q0 0 1
State Input X
00 0 1 00 X X
Q1Q0 0 1
01 X X 01 1 1
00 0X, 0X 0X, 1X
11 X X 11 1 0
01 0X, X1 1X, X1
10 0 1 10 X X
10 X1, 0X X0, 1X
J0 K0
11 X1, X1 X0, X0
J0 = X K 0 = Q1 + X
J1K1,J0K0

19. Transferring onto K-maps to derive output
equation
Excitation/output table
State Input X Output
Q1Q0 0 1 Z
00 0X, 0X 0X, 1X 0
01 0X, X1 1X, X1 0 Z = Q1⋅ Q0
10 X1, 0X X0, 1X 0
11 X1, X1 X0, X0 1
J1K1,J0K0

20. Circuit (logic) diagram
excitation equations output equation
J 1 = Q0 ⋅ X K1 = X Z = Q1⋅ Q0
J0 = X K 0 = Q1 + X
X X' Q0 Q1'
Z
J0 Q0
J Q
K Q
K0
J1 Q1
J Q
K Q
Clk K1

21. Assigning state variable to obtain
transition/output table machine
Mealy
Transition/output table
State Input X
Change Q1Q0 0 1
of 00 00,0 01,0
Encoding
A = 00 01 00,0 11,0
B = 01 11 00,0 11,1
C = 11
Next State Q1*Q0*, Z
Choosing D
type flip flop

22. Constructing the excitation table
M ealy machine
Excitation/output table
State Input X
Q1Q0 0 1
00 00,0 01,0
01 00,0 11,0
11 00,0 11,1
D1D0, Z

23. Transferring onto K-maps to derive excitation
equations (Mealy Machine)
Excitation/ State Input X State Input X
output table Q1Q0 0 1 Q1Q0 0 1
State Input X
00 0 0 00 0 1
Q1Q0 0 1
01 0 1 01 0 1
00 00,0 01,0
11 0 1 11 0 1
01 00,0 11,0
10 X X 10 X X
11 00,0 11,1
D1 D0
D1D0, Z D1 = Q 0 ⋅ X D0 = X

24. Transferring onto K-maps to derive output
equation (Mealy Machine)
Excitation/output State Input X
table
Q1Q0 0 1
State Input X
00 0 0
Q1Q0 0 1
01 0 0
00 00,0 01,0
11 0 1
01 00,0 11,0
10 X X
11 00,0 11,1
Z
D1D0, Z Z = Q1 ⋅ X

25. Circuit (logic) diagram
Mealy machine
D0 = X D1 = Q0 ⋅ X excitation equations
Z = Q1 ⋅ X output equation
X
Z
D0 Q0
D Q
Q
D1 D Q Q1
Q
Clk

26. Example 1: State Diagram
• Design the FSM for the given state diagram
– Graphical version of states, inputs, transitions and
outputs
W Z
State
X Y assignment
Given state diagram Assigned state diagram
26

27. Example 1: State Table
• For each current-state, specify next-state(s) as
a function of the present inputs
• For each current-state, specify the output(s) as
a function of the present inputs
State Variables
We often use Q0, Q1,
Q2, etc. to acknowledge
that state variables are
F-F outputs
27

28. Example 1: Alternate State Table
• State table, alternate format emphasizing state
transitions
• Notation: A → Q(t) and A+ → Q(t+1), used to
indicate the change in state variable needed
for the desired transition
Q1(t) Q0(t) →
Q1(t+1) Q0(t+1) ( )
a more
descriptive
notation
28

29. Example 1: Flip-Flop Excitation Tables
• Use these tables to “move” Q to next state
• Used to design the memory control CL circuit
We will use the D F-F 29

30. Example 1: Flip-Flop Excitation Tables
• Why are we are interested in the D Flip-Flop
for this design?
Q(t) Q(t+1) D Operation
0 0 0 Reset
0 1 1 Set
1 0 0 Reset
1 1 1 Set
We select D Flip-Flops because the D input is
simply the value of Q(t+1) that we desire
30

31. Example 1: Block Diagram
• We need to use two
D flip-flops x y
(output)
• The sequential circuit
would look as shown (next state)
Q1 D1
• We will design the CL
for a 3-input, 3-output Q2 D2
circuit
– CL for Output (y)
– CL for Next State
controls (D1 and D2)
inputs = x, Q1, Q2
outputs = y, D1, D2
31

32. Example 1: Truth Table
• The truth table for this 3-input, 3-output circuit
can be generated from the original state table
• We will need to minimize each output function
using Karnaugh maps, mindful of overlap
0
1
2
3
minterms 4
5
6
7 32

33. Example 1: Karnaugh Maps
• Minimizing each of the three outputs:
A+ B+
1 1 1 1 1
A+ = x ∙ Q1 + x ∙ Q2 B+ = x ∙ Q1
y
A = Q1 and B = Q2
1 1 1
y = x ∙ Q1 + x ∙ Q2 33

34. Example 1: Circuit Diagram
• The circuit that results from these equations is
shown below:
y = x ∙ Q1 + x ∙ Q2
y = x ∙ (Q1 + Q2)
A+ = x ∙ Q1 + x ∙ Q2
A+ = x ∙ (Q1 + Q2)
B+ = x ∙ Q1
34

35. Design: Example 2
• Given the state diagram as follows, design the
sequential circuit using JK Flip-Flops
D
A C
B state assignment
A = 01
B = 10
C = 11
D = 00
35

36. Design: Example 2
• Note that this is a state diagram for a Mealy machine
inputs outputs
36

37. Design: Example 2
• Block diagram, signal identification
Input, x Sequential
Logic
1-bit Circuit
CP
We need to
determine
what goes in
here? 37

38. Design: Example 2
• From state table, get input flip-flop function
KB = Ax + A’x’
KB = Ax + A’x’ 38

39. Design: Example 2
• Input flip-flop function
JA
Input, x A
B
KA
x JB
• Logic Diagram 1-bit KB
CP
x
x′ B A x
x B
39

40. CLK
QA
QD
QC
QB
0 1 2 3 4 8 9 10 11 12 0
101 overlap M oore machine
1 1
A 1 B 0 C0 1 C1
0
0 0 0 1
0
0

41. CLK
QD
QC
QB
QA
LD
5 6 7 8 9 10 11 12 13 14 5
Initial Counting Reloading
Loading starts

42. 1110 Moore machine
1
0 1
A 1 B 1 C 1 D 0 E
0 0 0 0
0 0 1
0 0

43. 43

44. State Input X
Output
S 0 1
Z
A A B
0
B A C0
0
C A C1
0
D A C1
1
Next State S*
44

45. X Q0 Q1
X' Q0'
D0 Q0
D Q
Q
D1 D Q Q1
Q
D2 D Q Q2 Z
Clk Q

46. State Input X Output
S 0 1 Z
A A B 0
B A C0 0
C0 A C1 0
C1 A C1 1
Next State S*
46