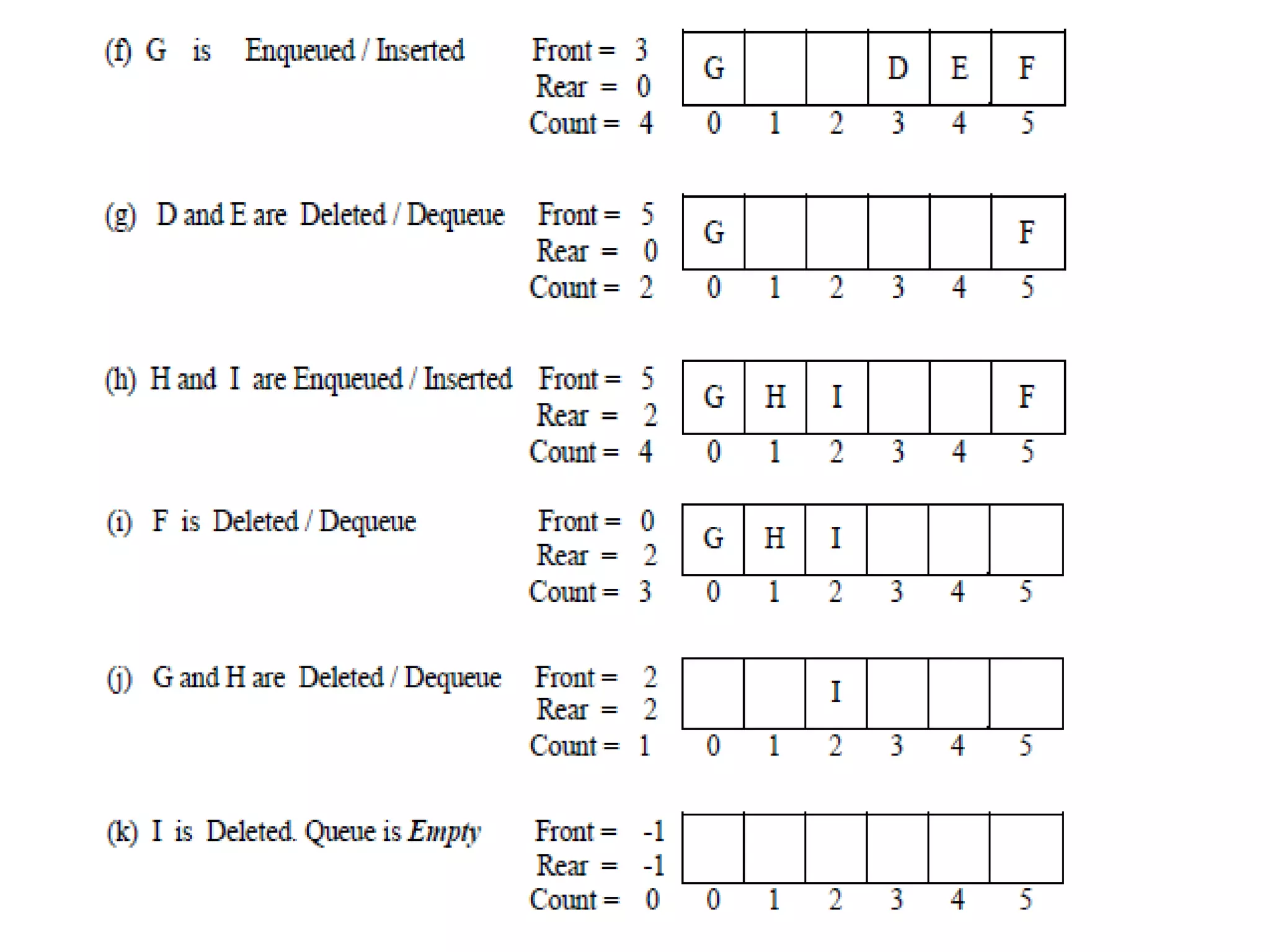
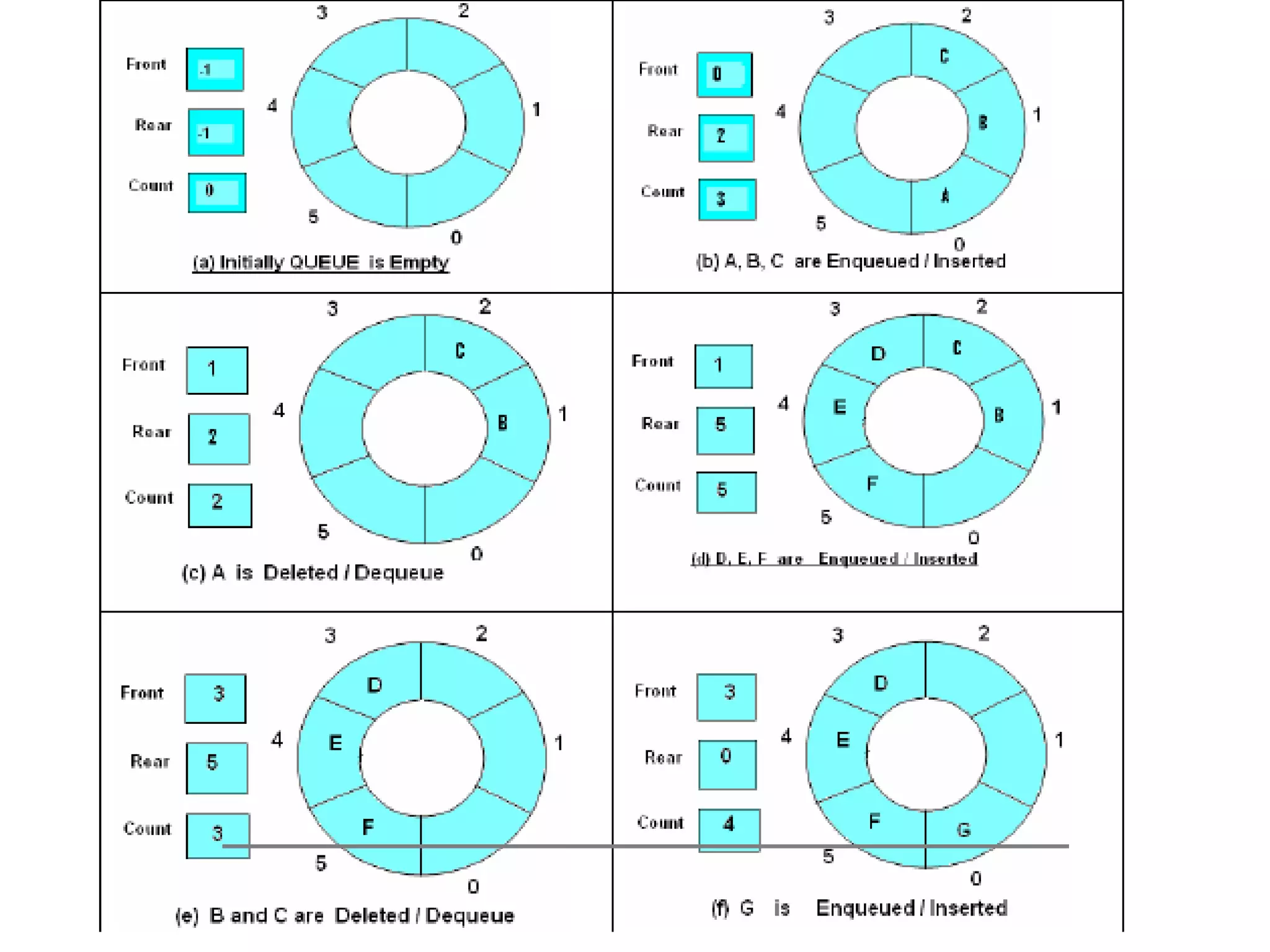
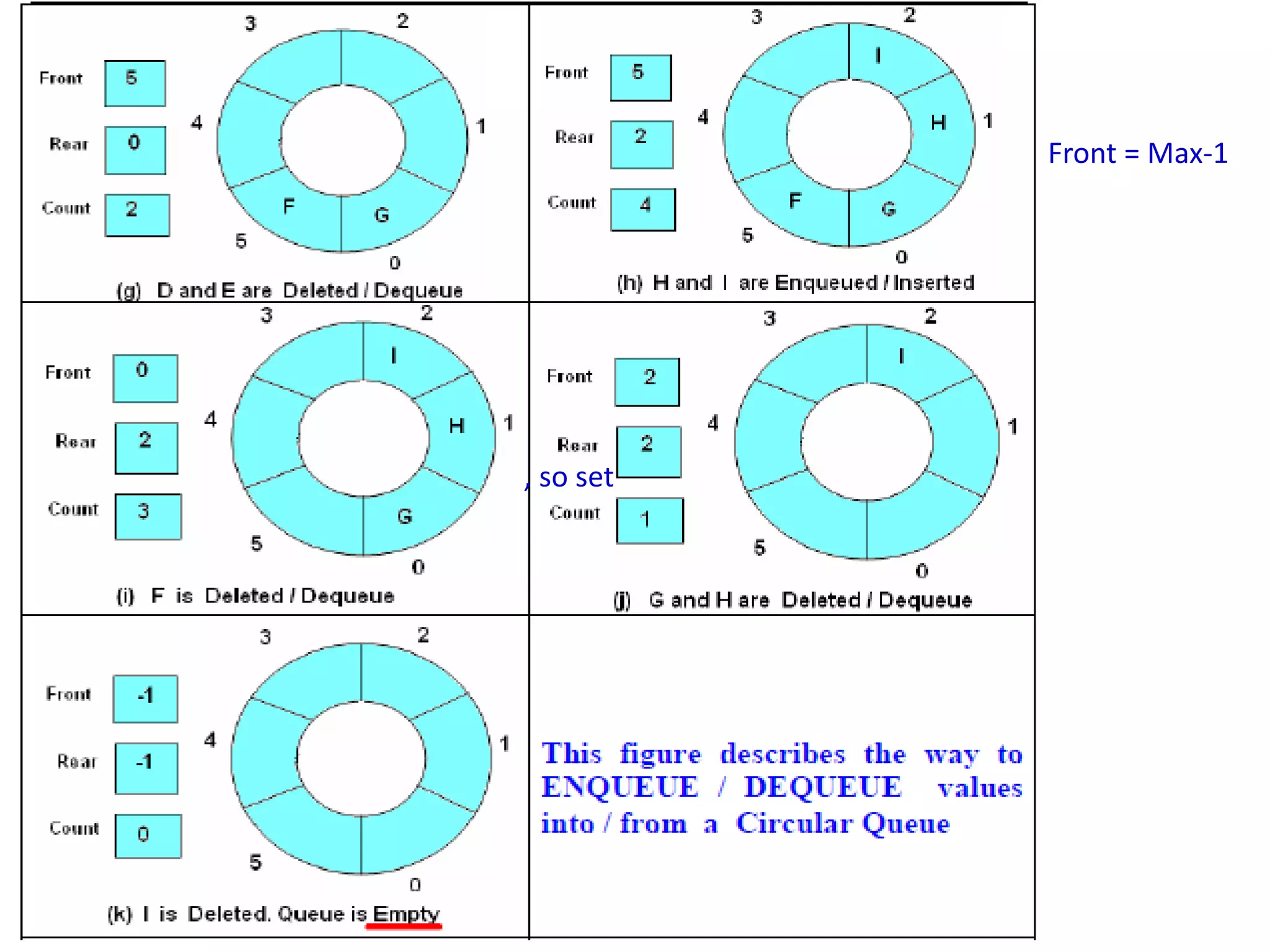
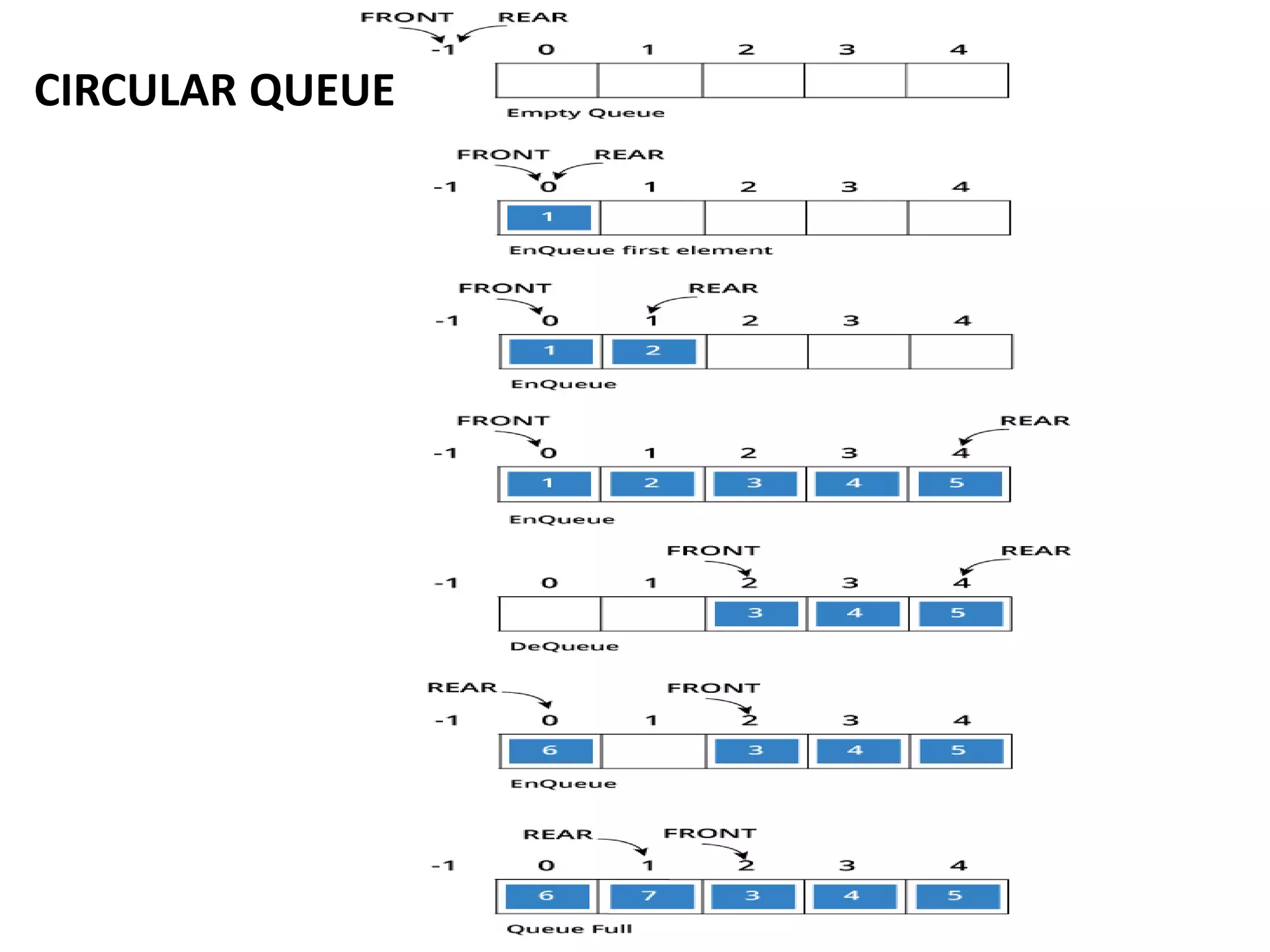
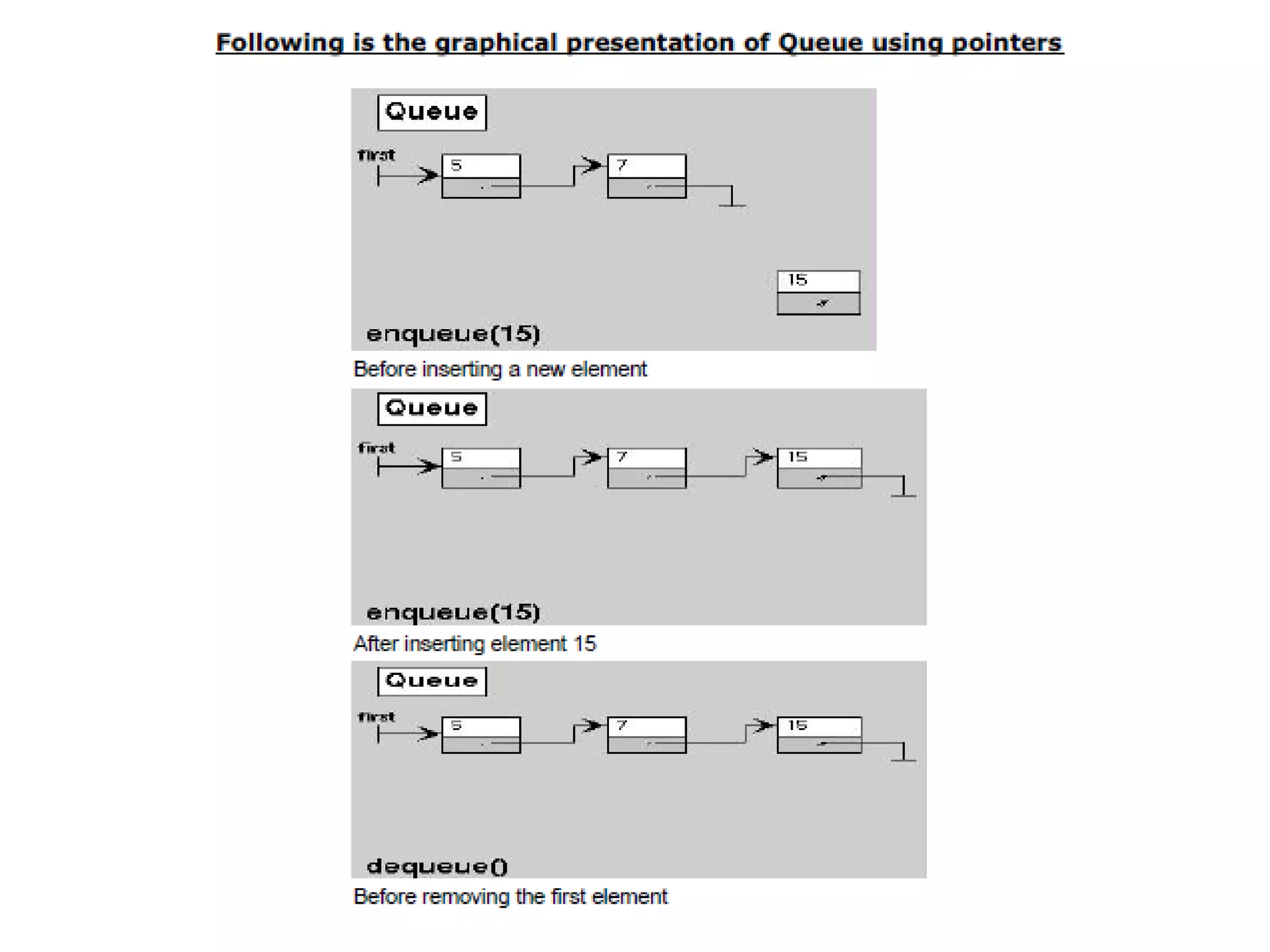
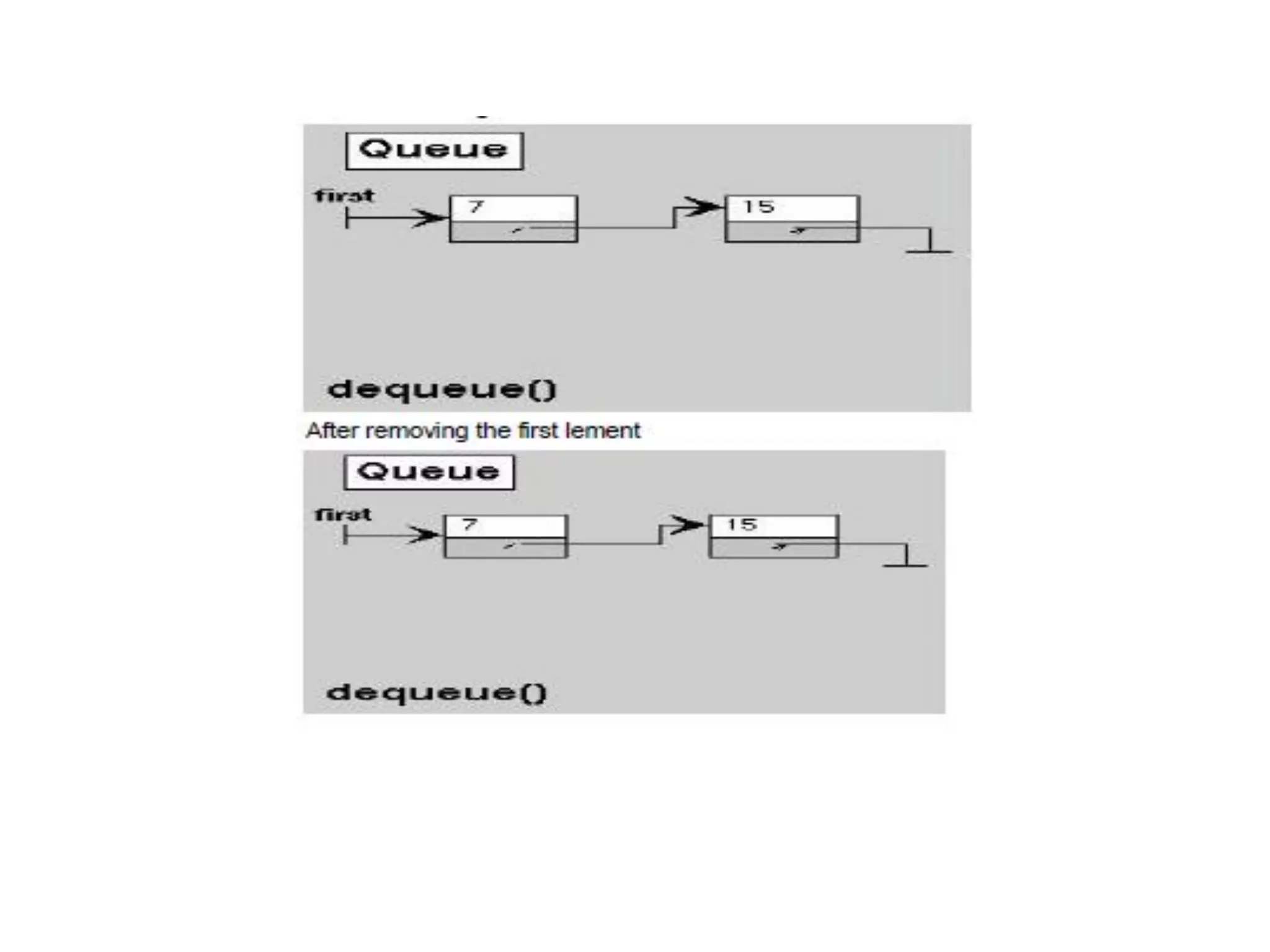
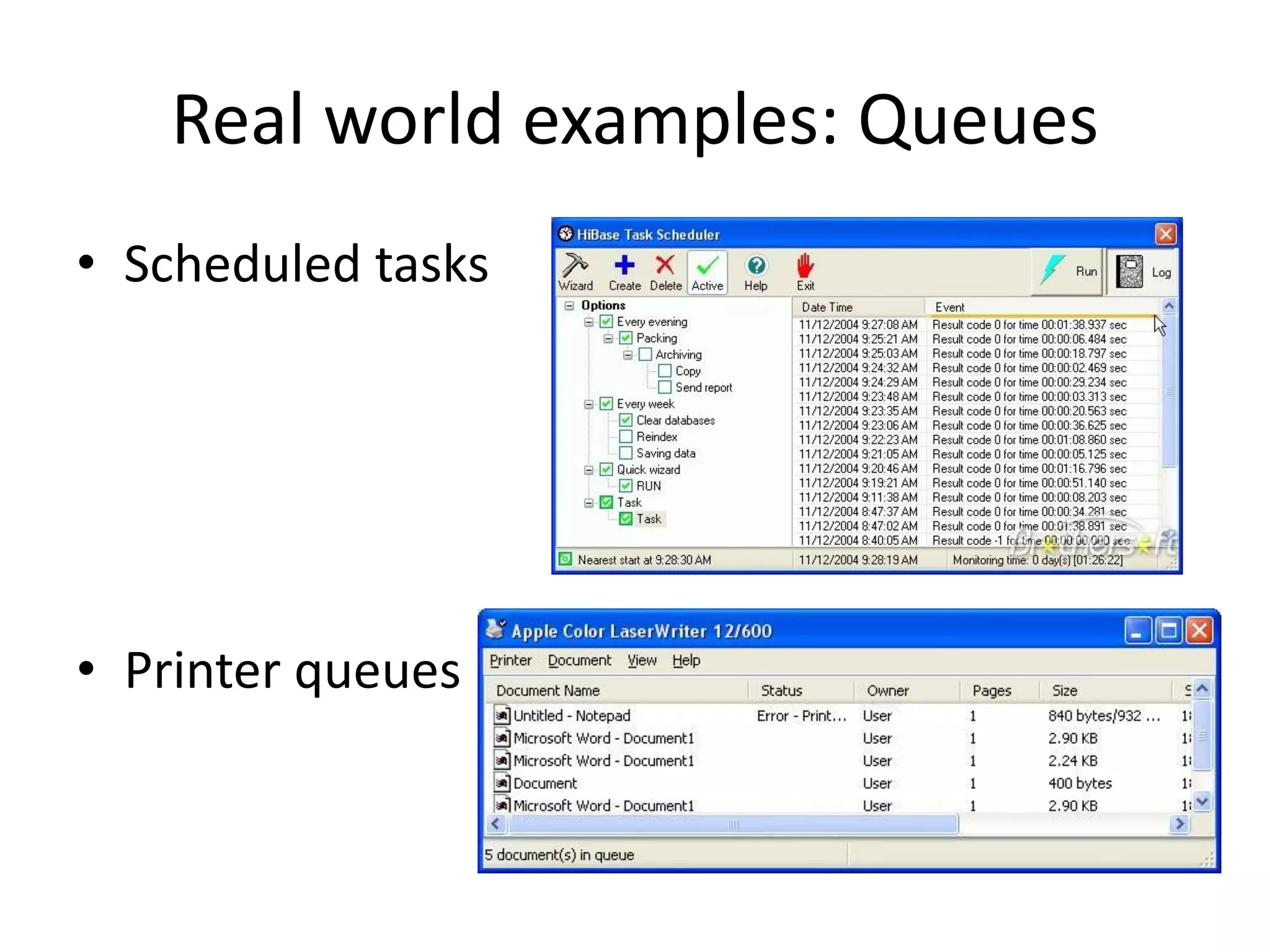
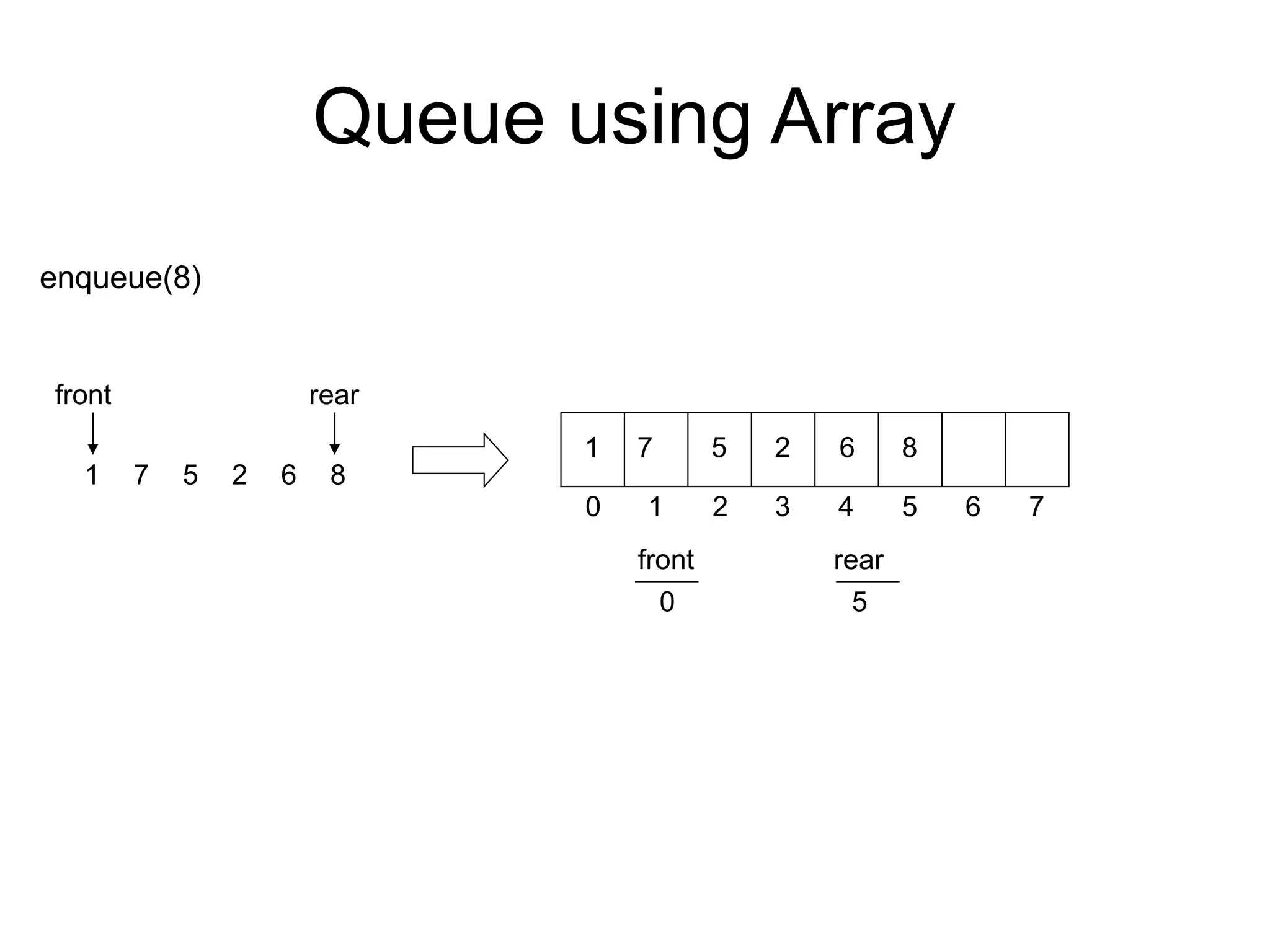
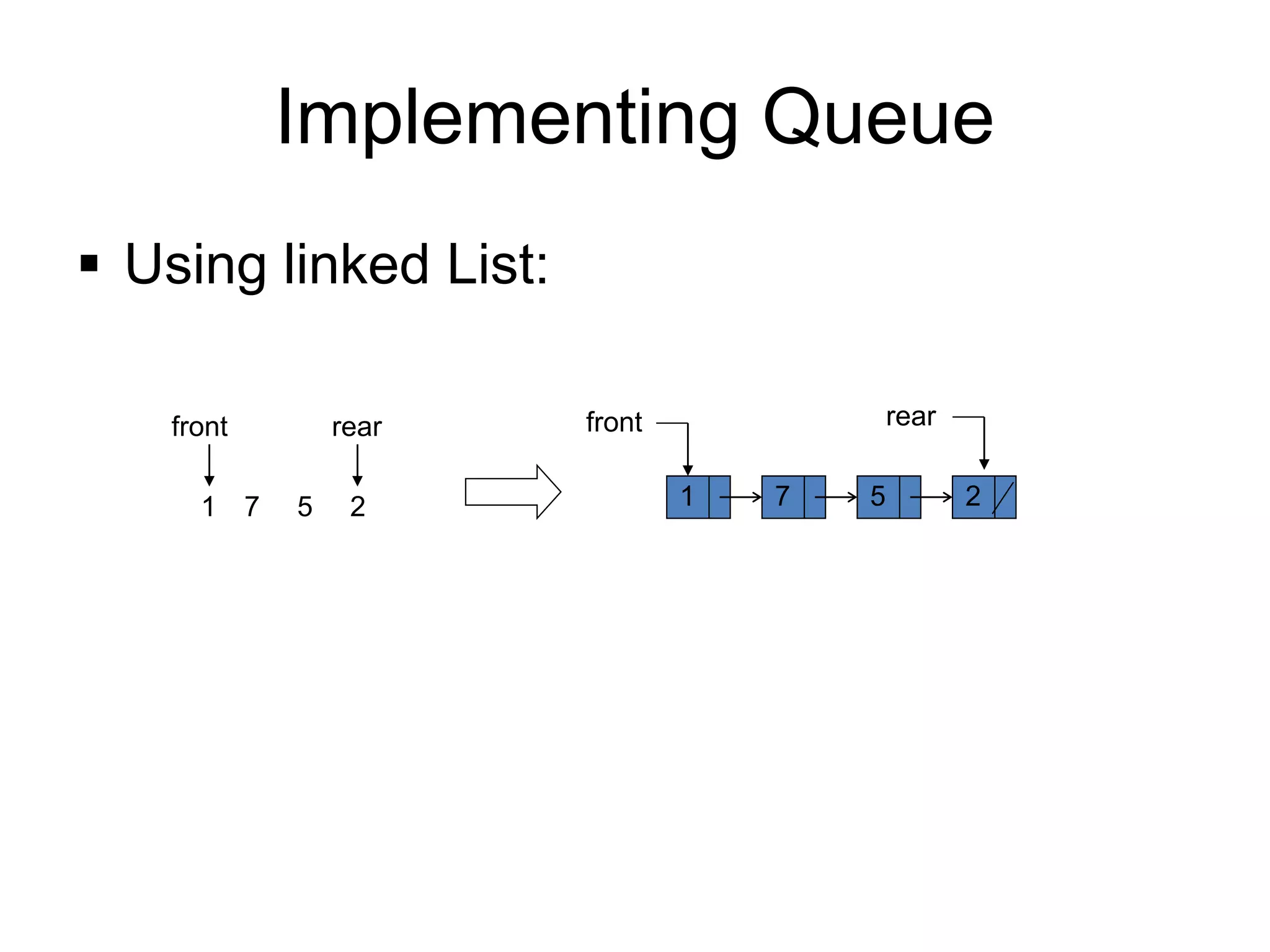
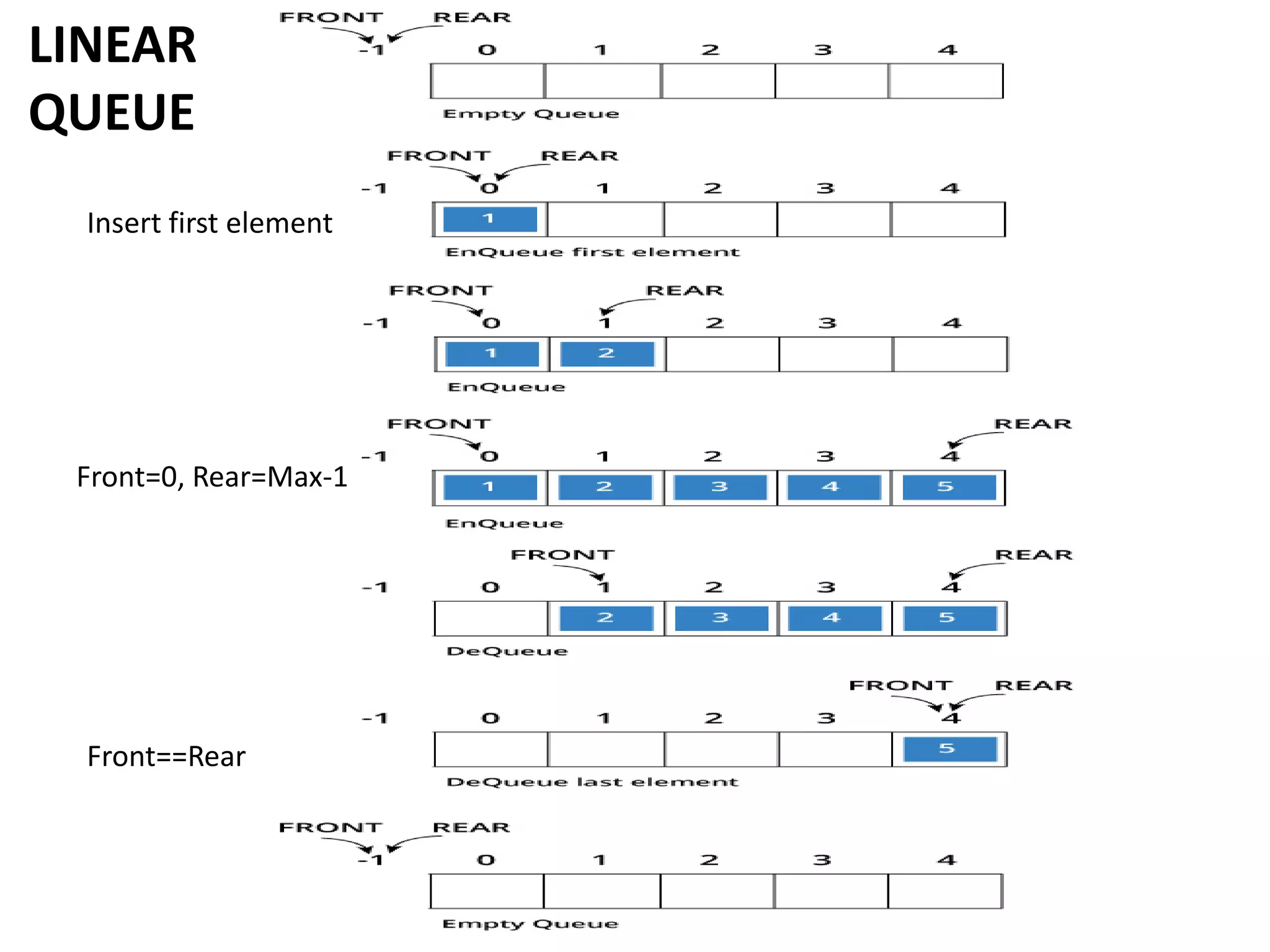
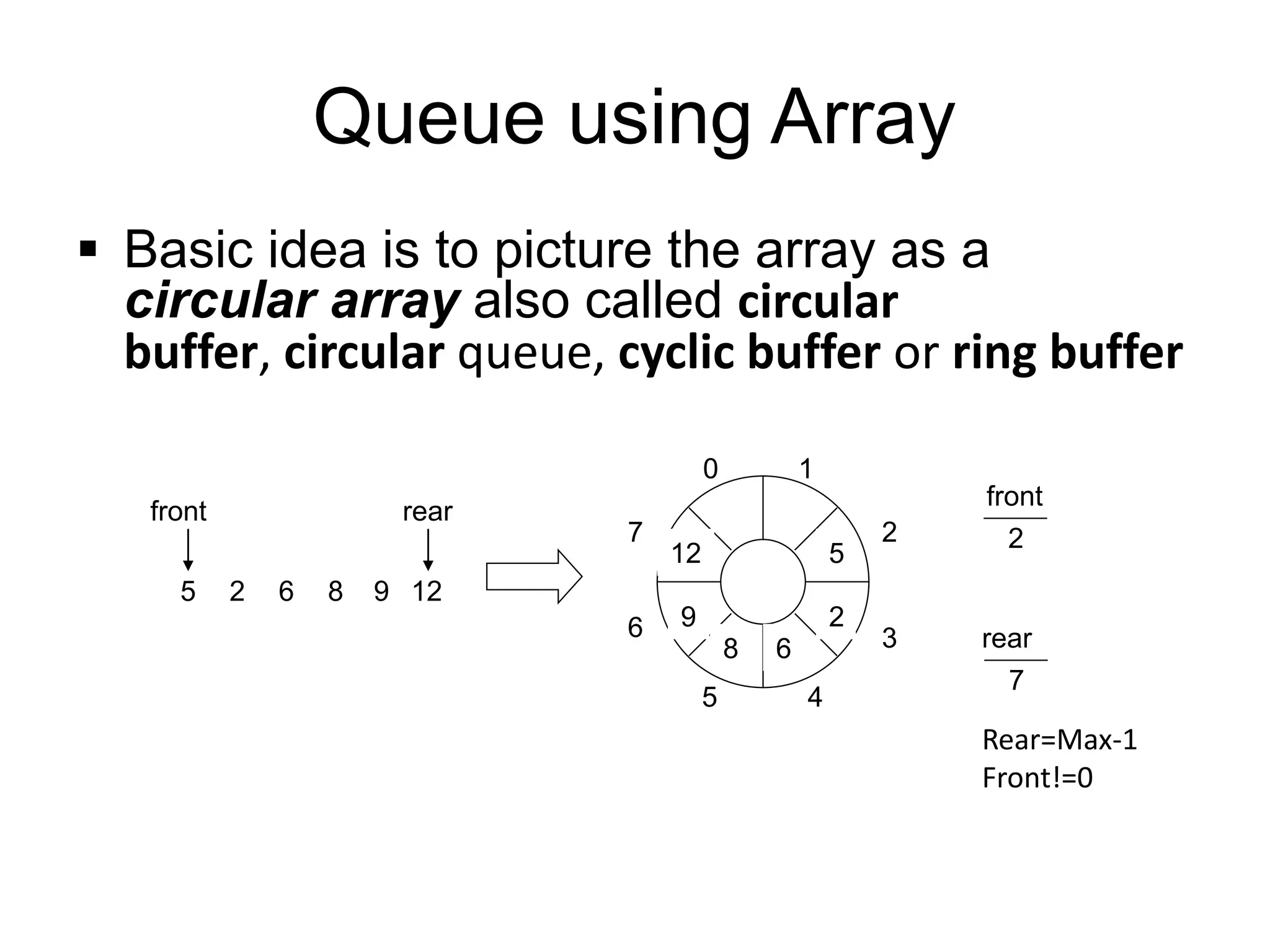
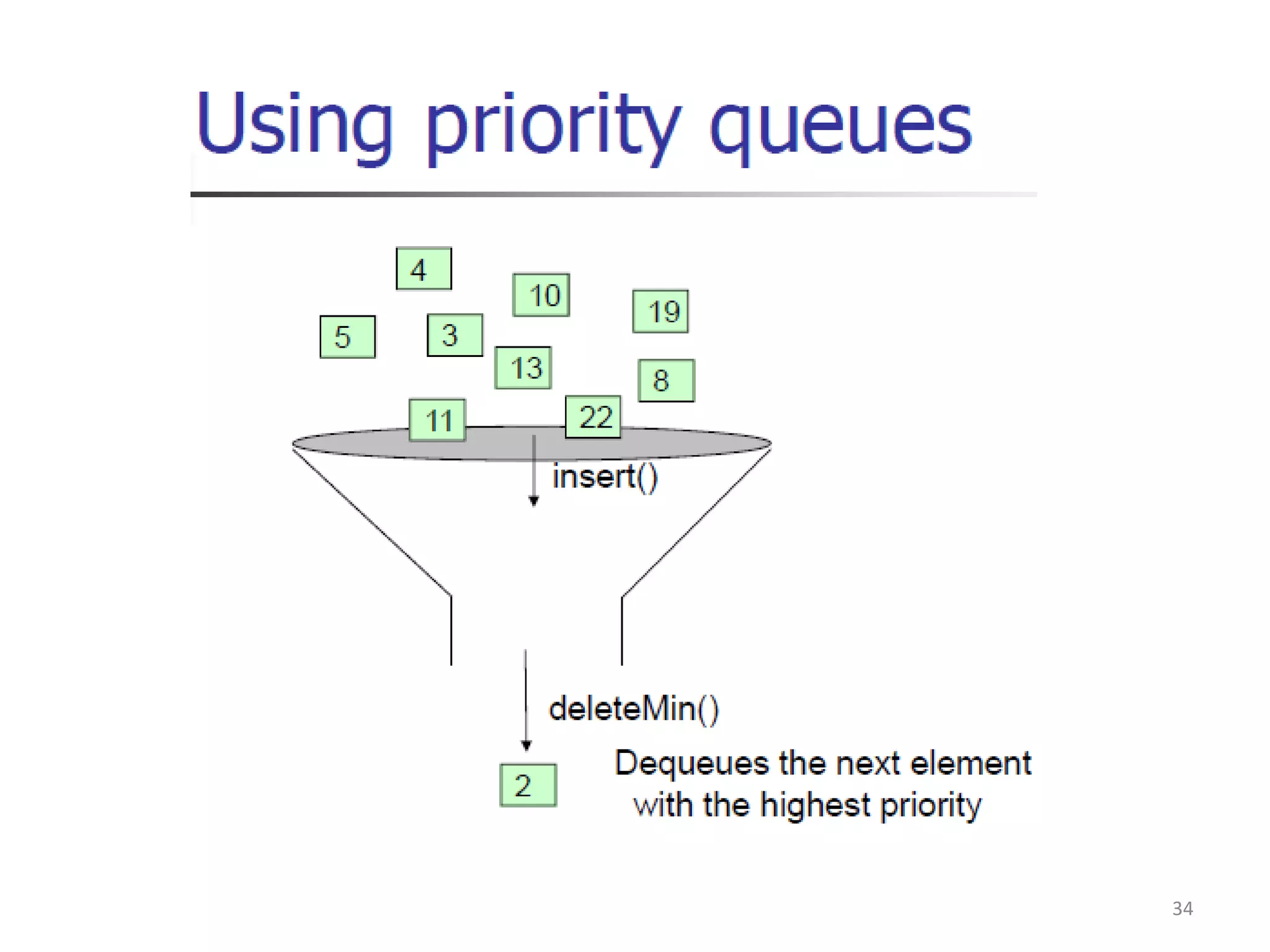
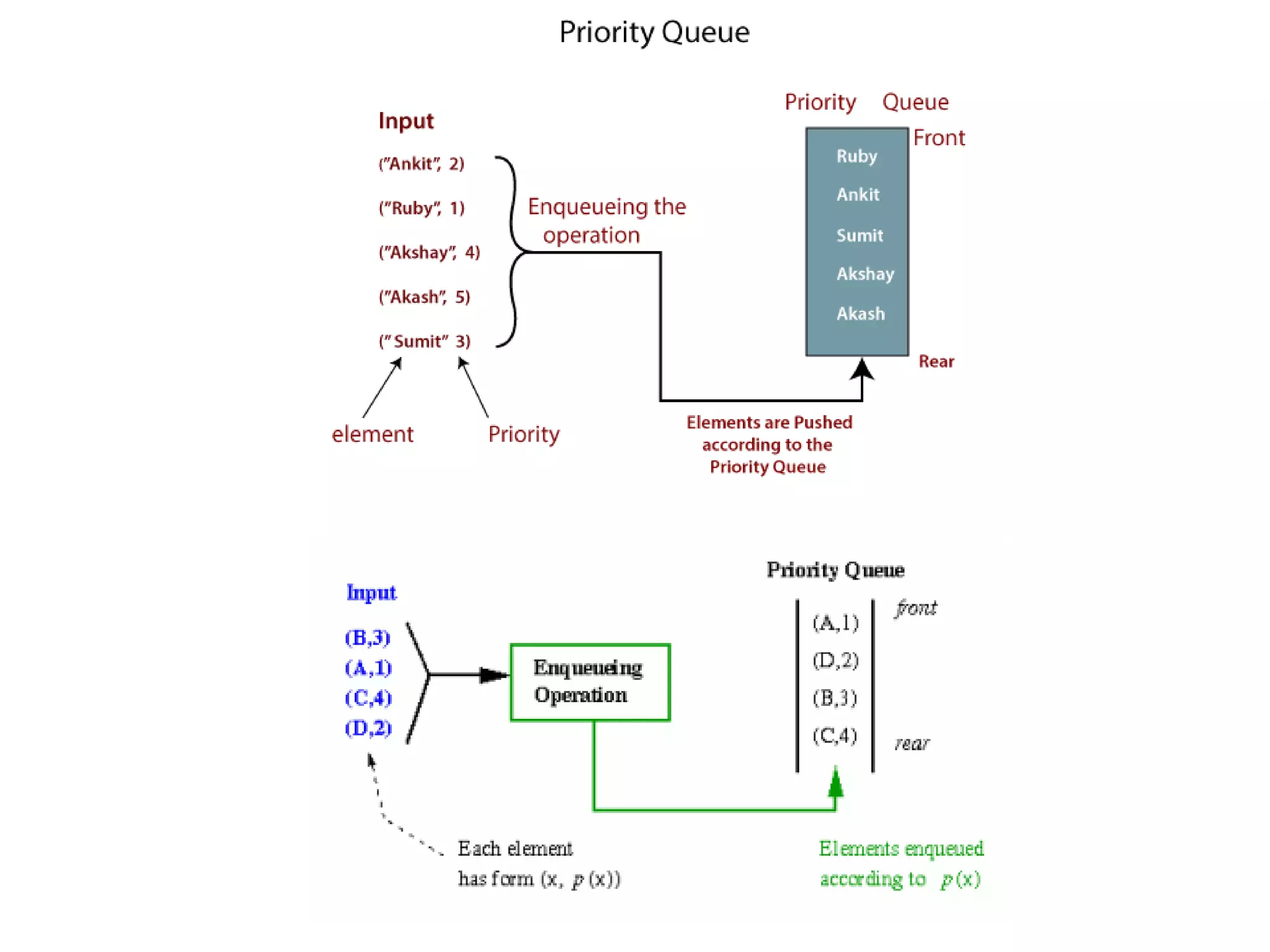
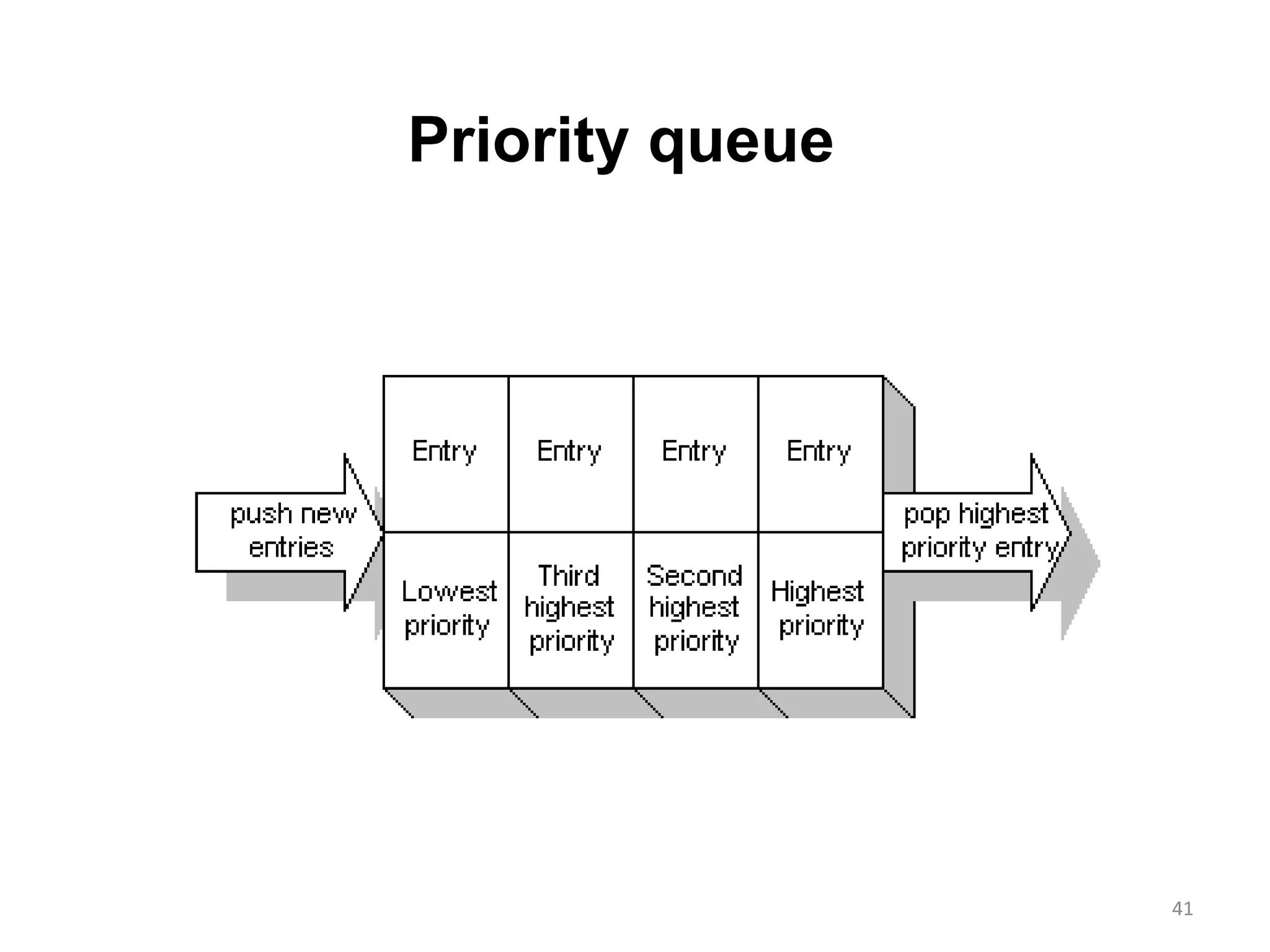
- Queues follow a First-In First-Out (FIFO) ordering principle where elements are inserted at the rear and removed from the front. - Queues can be implemented using arrays or linked lists. Circular queues use arrays to avoid empty space issues. - Priority queues order elements by priority rather than insertion order, with the highest priority element removed first. They have applications like job scheduling.

1. Data Structures & Algorithm
CSC-102
Lecture 4
Queues
&
Priority Queues
Lecturer: Syeda Nazia Ashraf 1

2. Queues
• A stack is LIFO (Last-In First Out) structure.
• In contrast, a queue is an abstract data type that stores
elements in a FIFO (First-In First-Out) order.
• A queue is a linear structure for which items can be only
inserted at one end and removed at another end.
• In other words, the order in which elements enters a queue is
the order in which they leave.
• There are main two ways to implement a queue :
1. Circular queue using array
2. Linked Structures (Pointers)
• Primary queue operations:
• Enqueue: insert an element at the rear of the queue
• Dequeue: remove an element from the front of the queue

3. Queue Operations
Enqueue(X) – place X at the rear of the
queue.
Dequeue() -- remove the front element and
return it.
Front() / Peek() --return front element
without removing it.
IsEmpty() -- return TRUE if queue is
empty, FALSE otherwise

4. Implementing Queue
▪ Using linked List: Recall
▪ Insert works in constant time for either end
of a linked list.
▪ Remove works in constant time only.
▪ Seems best that head of the linked list be
the front of the queue so that all removes
will be from the front.
▪ Inserts will be at the end of the list.

5. Implementing Queue
▪ Using linked List:
front
2
5
7
1 1 7 5 2
front
rear rear

6. Implementing Queue
▪ Using linked List:
front
2
5
7
1 1 7 5 2
front
rear rear
front
2
5
7 1 7 5 2
front
rear rear
dequeue()

7. Implementing Queue
▪ Using linked List:
front
2
5
7
1 1 7 5 2
front
rear rear
front
2
5
7 9
7 5 2
front
rear rear
enqueue(9)
9

8. Real world examples: Queues
• Tech Support helplines

9. Real world examples: Queues
• Scheduled tasks
• Printer queues

10. Queue using Array
▪ If we use an array to hold queue elements,
both insertions and removal at the front
(start) of the array are expensive.
▪ This is because we may have to shift up to
“n” elements.
▪ For the stack, we needed only one end; for
queue, we need both.
▪ To get around this, we will not shift upon
removal of an element.

11. LINEAR
QUEUE
Front=0, Rear=Max-1
Insert first element
Front==Rear

12. Queue using Array
front
2
5
7
1
rear
6
5 7
0
0 1 3
2 4
front
1 7 5 2
3
rear

13. Queue using Array
front
2
5
7
1
rear
6
5 7
0
0 1 3
2 4
front
1 7 5 2
4
rear
enqueue(6)
6
6

14. Queue using Array
front
2
5
7
1
rear
6
5 7
0
0 1 3
2 4
front
1 7 5 2
5
rear
enqueue(8)
6
6
8
8

15. Queue using Array
front
2
5
7
rear
6
5 7
1
0 1 3
2 4
front
7 5 2
5
rear
dequeue()
6
6
8
8

16. Queue using Array
front
2
5
rear
6
5 7
2
0 1 3
2 4
front
5 2
5
rear
dequeue()
6
6
8
8

17. Queue using Array
front
2
5
rear
6
5 7
2
0 1 3
2 4
front
5 2
7
rear
enqueue(9)
enqueue(12)
6
6
8
8
9
9
12
12
enqueue(21) ??
Rear=Max-1
Front!=0

18. Queue using Array
▪ We have inserts and removal running in
constant time but we created a new
problem.
▪ Cannot insert new elements even though
there are two places available at the start
of the array.
▪ Solution: allow the queue to “wrap
around”.

19. Queue using Array
▪ Basic idea is to picture the array as a
circular array also called circular
buffer, circular queue, cyclic buffer or ring buffer
front
2
5
rear
2
front
7
rear
6 8 9 12
6
5
7
0 1
3
2
4
5
2
6
8
9
12
Rear=Max-1
Front!=0

20. Circular Queue using Array
front
2
5
rear
2
front
0
rear
6 8 9 12
6
5
7
0 1
3
2
4
5
2
6
8
9
12
enqueue(21)
21
21
8
size
7
noElements

21. Circular Queue using Array
front
2
5
rear
2
front
1
rear
6 8 9 12
6
5
7
0 1
3
2
4
5
2
6
8
9
12
enqueue(7)
21
21
8
size
8
noElements
7
7
Rear=Front-1

22. Circular Queue using Array
front rear
4
front
1
rear
6 8 9 12
6
5
7
0 1
3
2
4
6
8
9
12
dequeue()
21
21
8
size
6
noElements
7
7

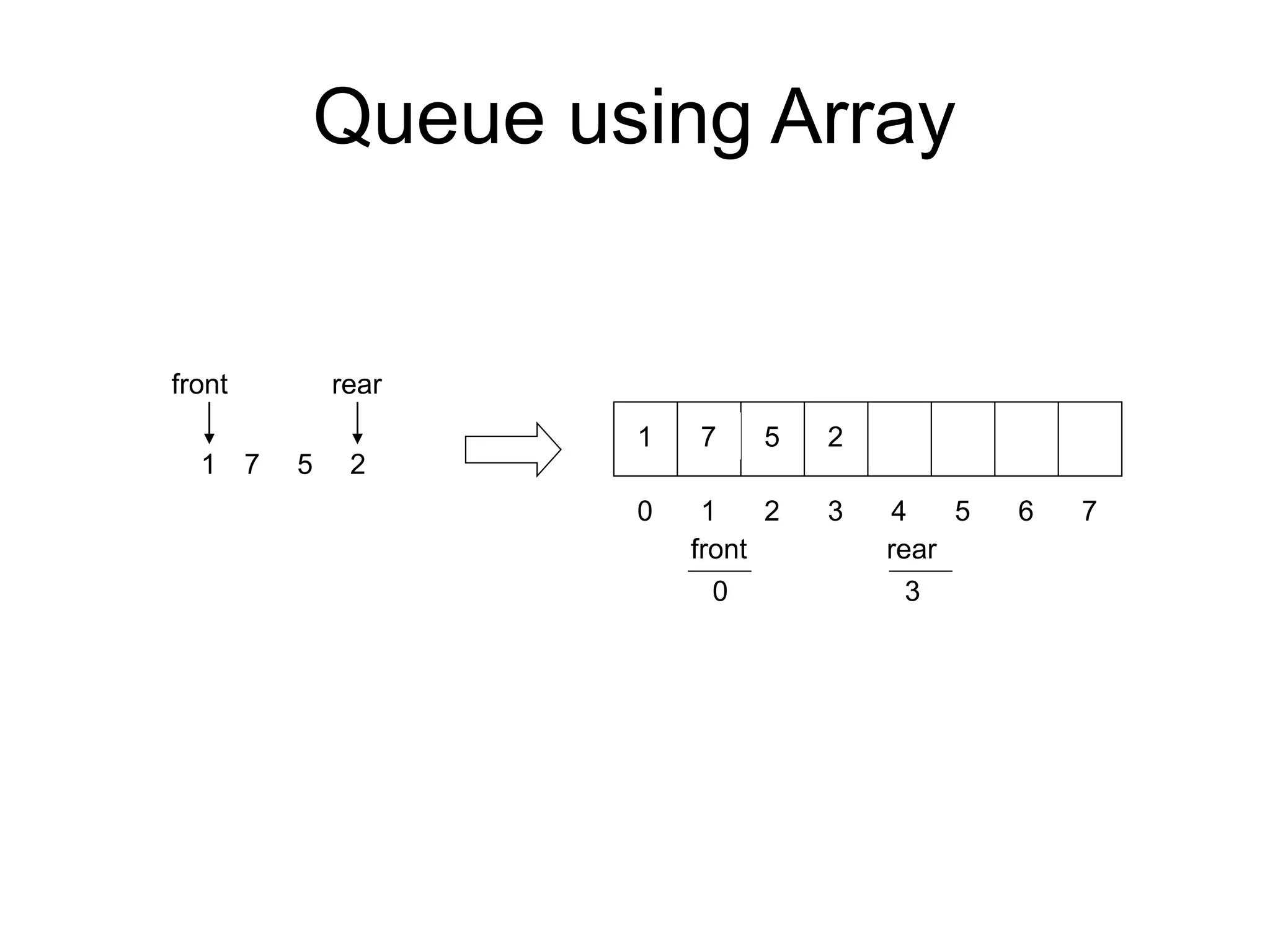
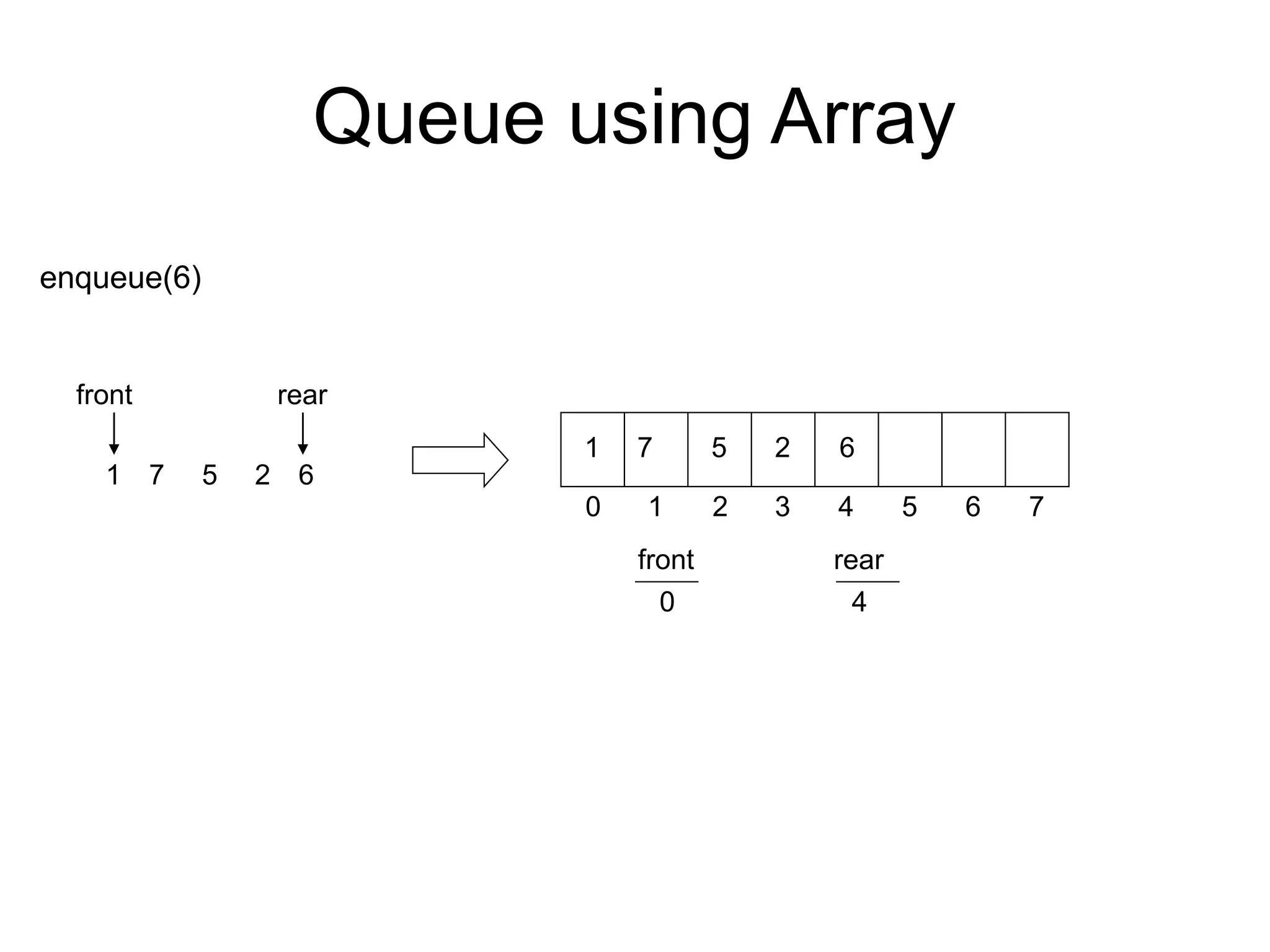
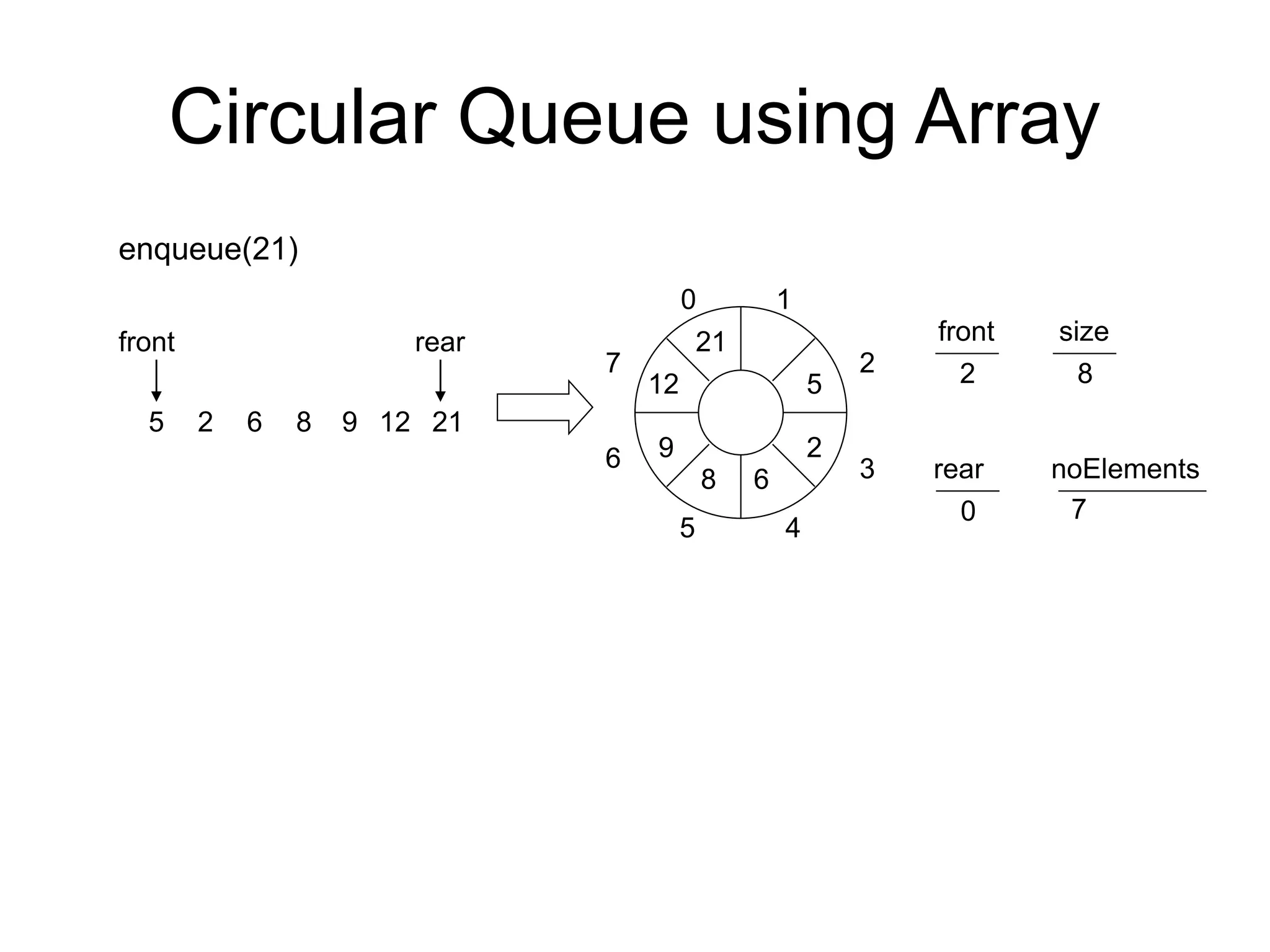
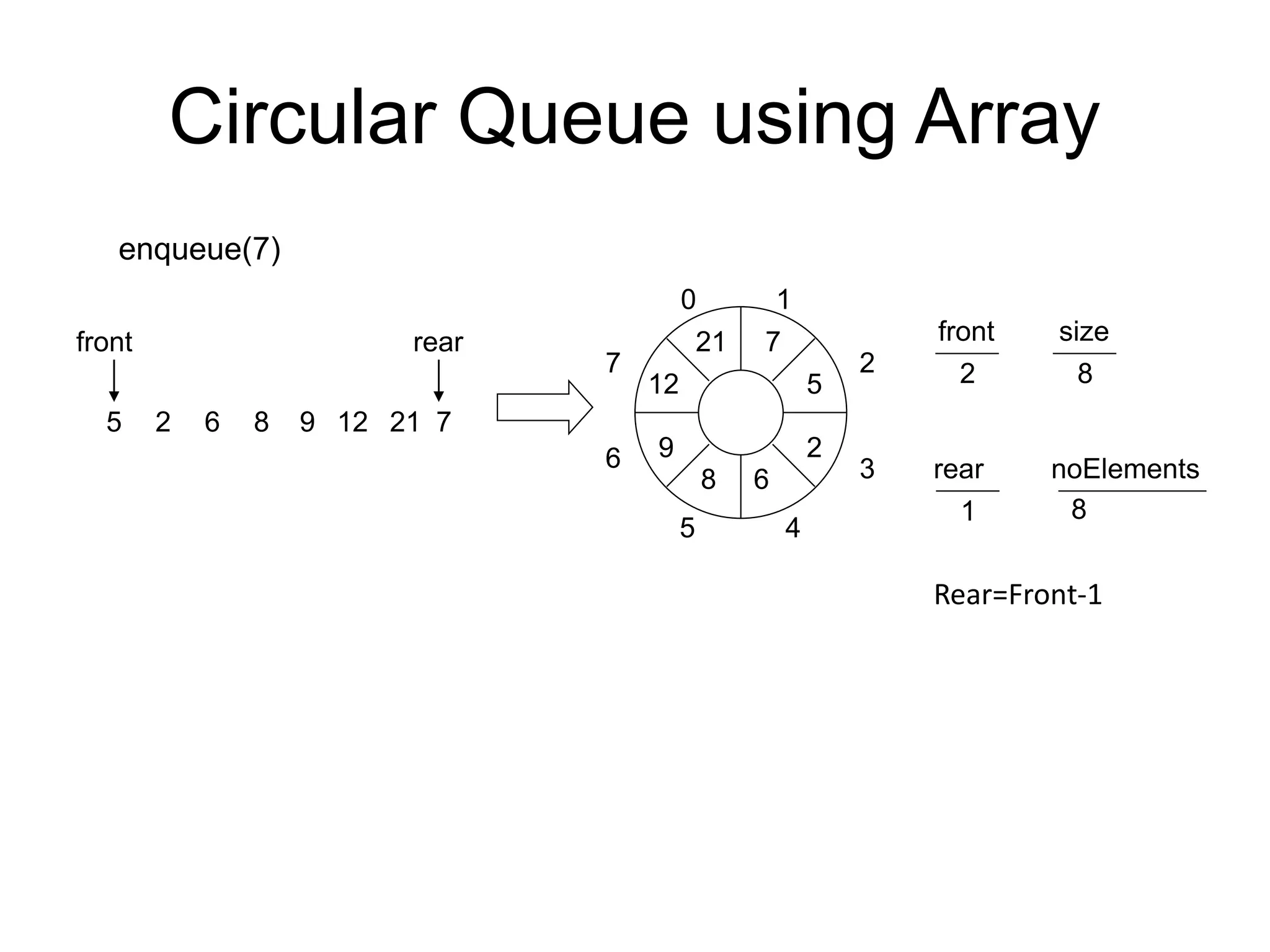
23. Following is the algorithm which describes the implementation of Queue using an Array.
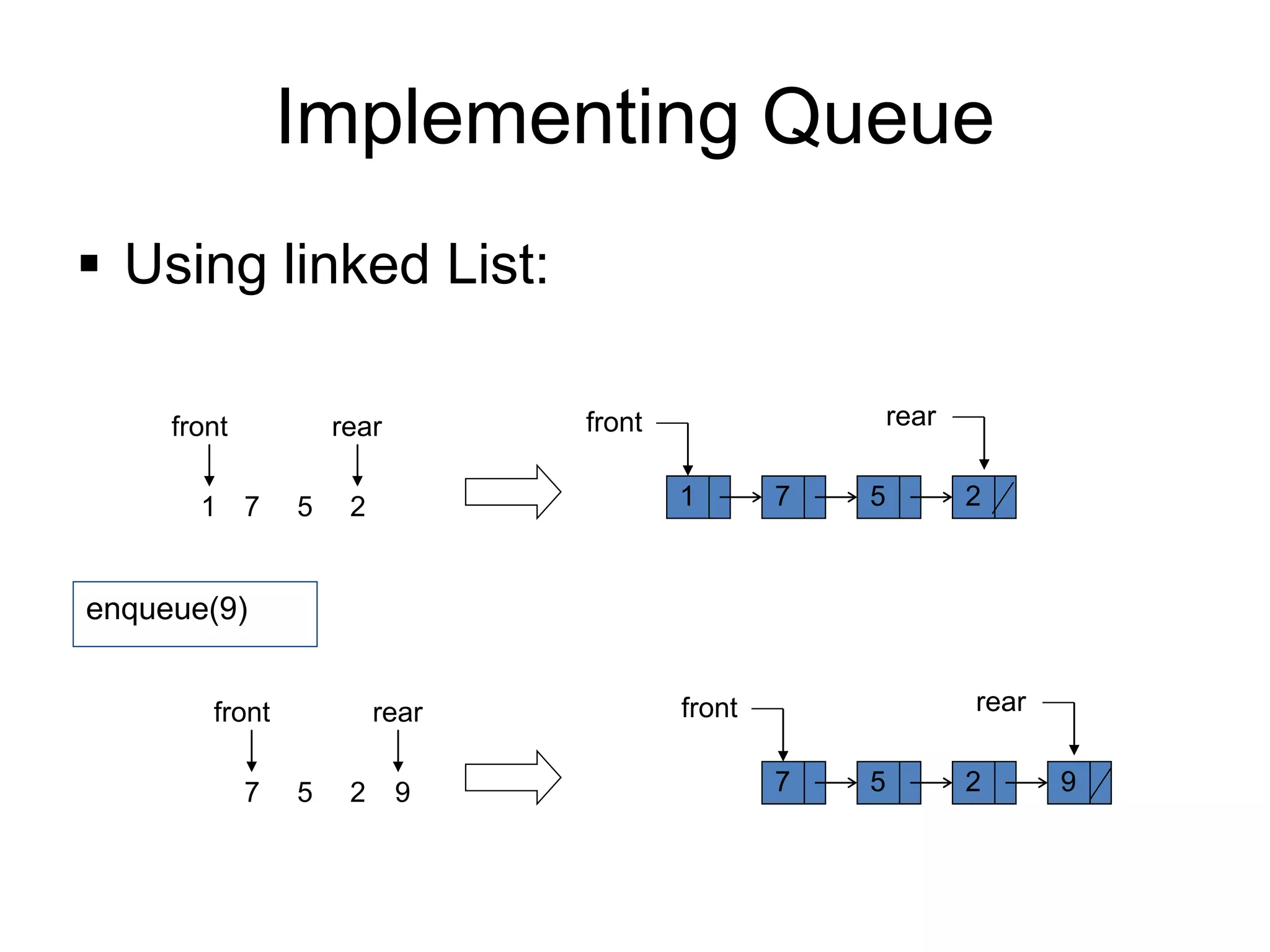
Insertion in Queue:
Algorithm: ENQUEUE(QUEUE, MAXSIZE, FRONT, REAR,COUNT, ITEM)
This algorithm inserts an element ITEM into a circular queue.
1. INITIALIZE FRONT=-1, REAR=-1
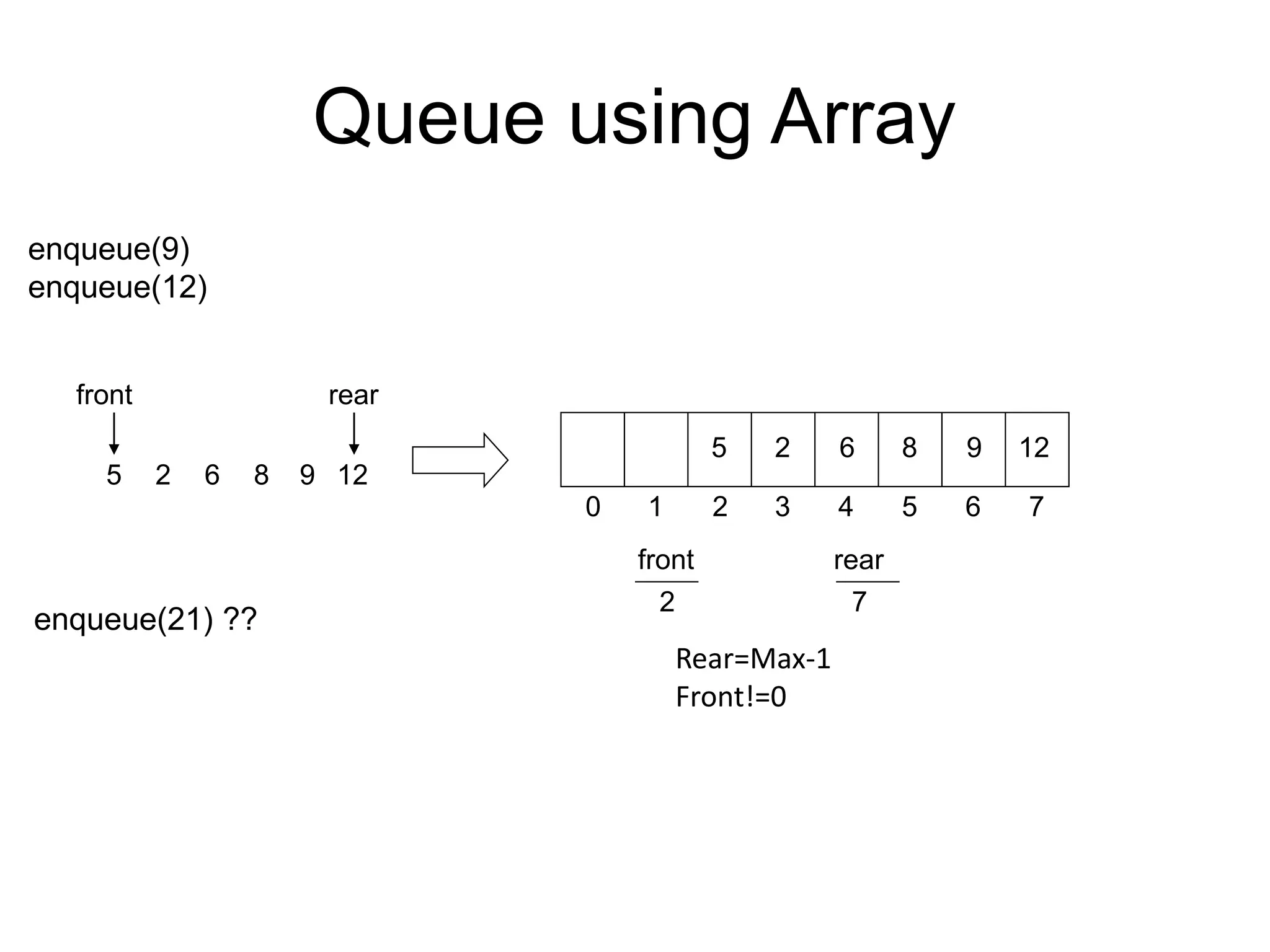
2. [QUEUE already filled?]
If COUNT = MAXSIZE || (FRONT = 0 && REAR == MAXSIZE – 1) || REAR =FRONT- 1 then:
[ COUNT is number of values in the QUEUE] [when REAR starts from 0 due to
circular increment and when its value is just 1 less than FRONT, the queue is full.]
Write: OVERFLOW, and Return.
2. [Find new value of REAR.]
If COUNT= 0 || FRONT=-1, then: [Queue initially empty.]
Set FRONT= 0 or REAR = 0 [Insert first element]
Else if REAR = MAXSIZE – 1 && FRONT!=0, then: [If REAR is at top of the array QUEUE]
Set REAR = 0 [Wrap Around to the bottom of the array QUEUE: the next element is
entered at QUEUE[0] incase that spot is free. This is done by setting
REAR=-1, so when the increment occurs, REAR will become 0]
Else:
Set REAR = REAR+1.
[End of If Structure.]
3. Set QUEUE[REAR] = ITEM. [This insert new element.]
4. COUNT=COUNT+1 [ Increment to Counter. ]
5. Return.

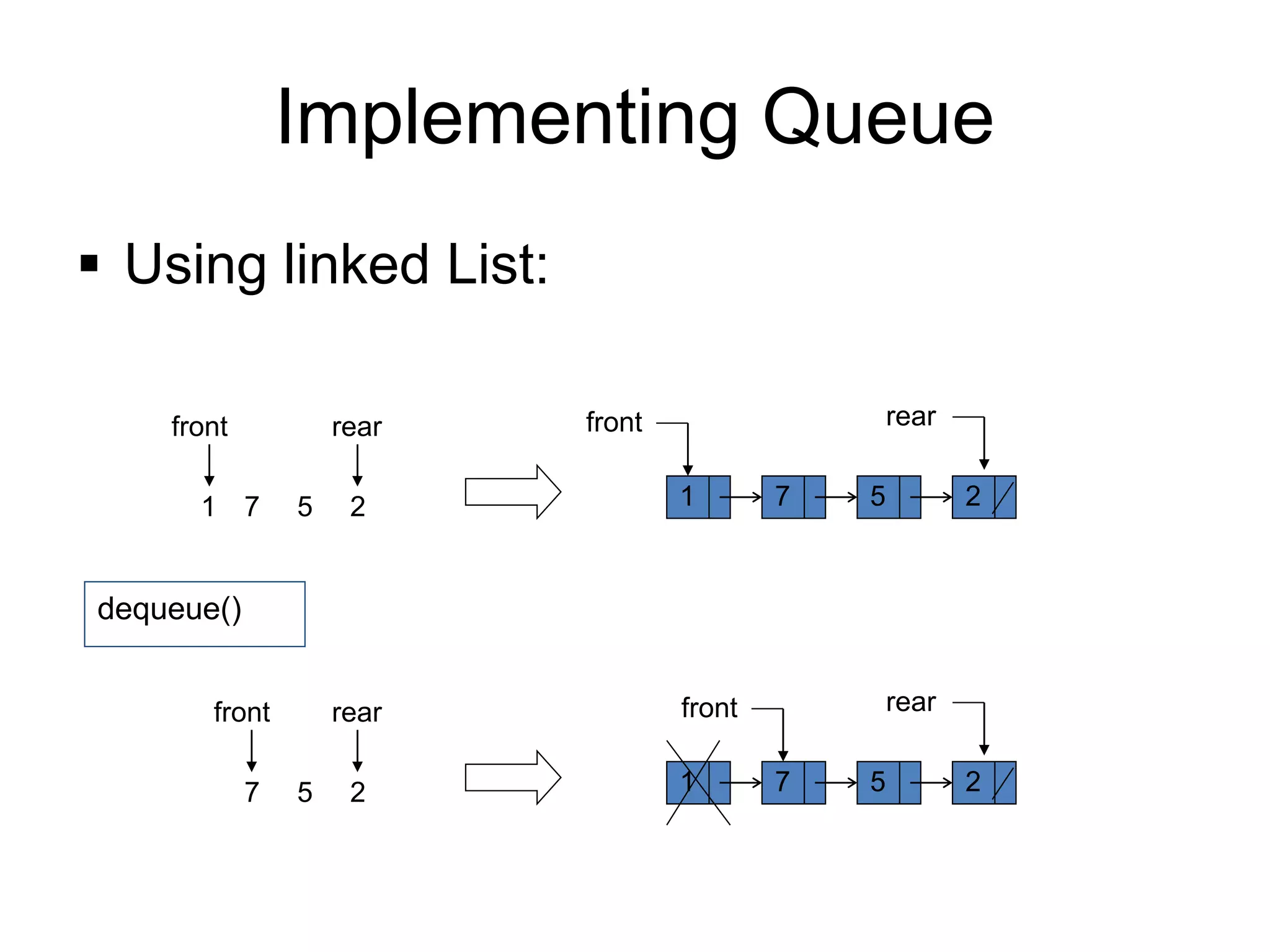
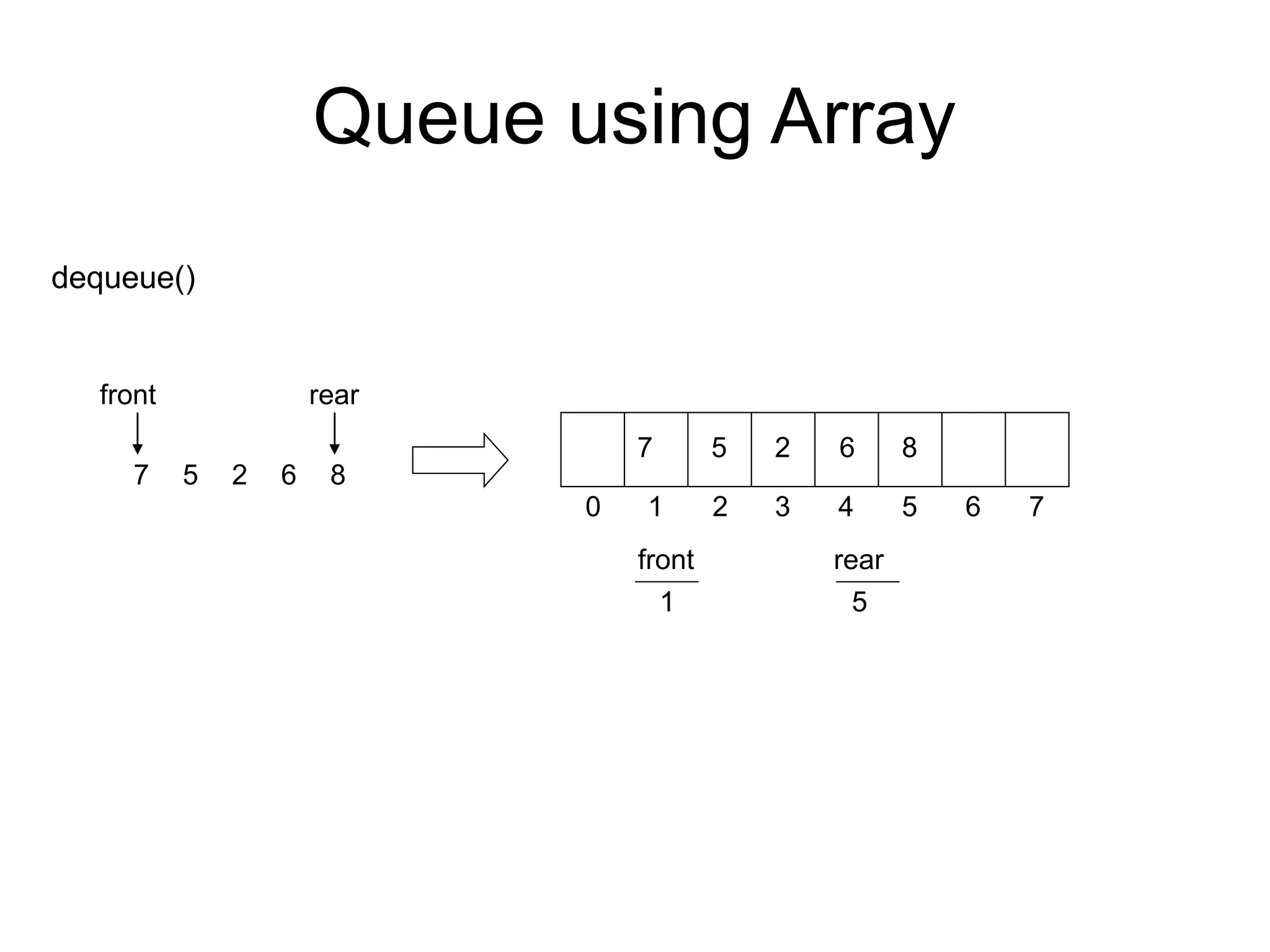
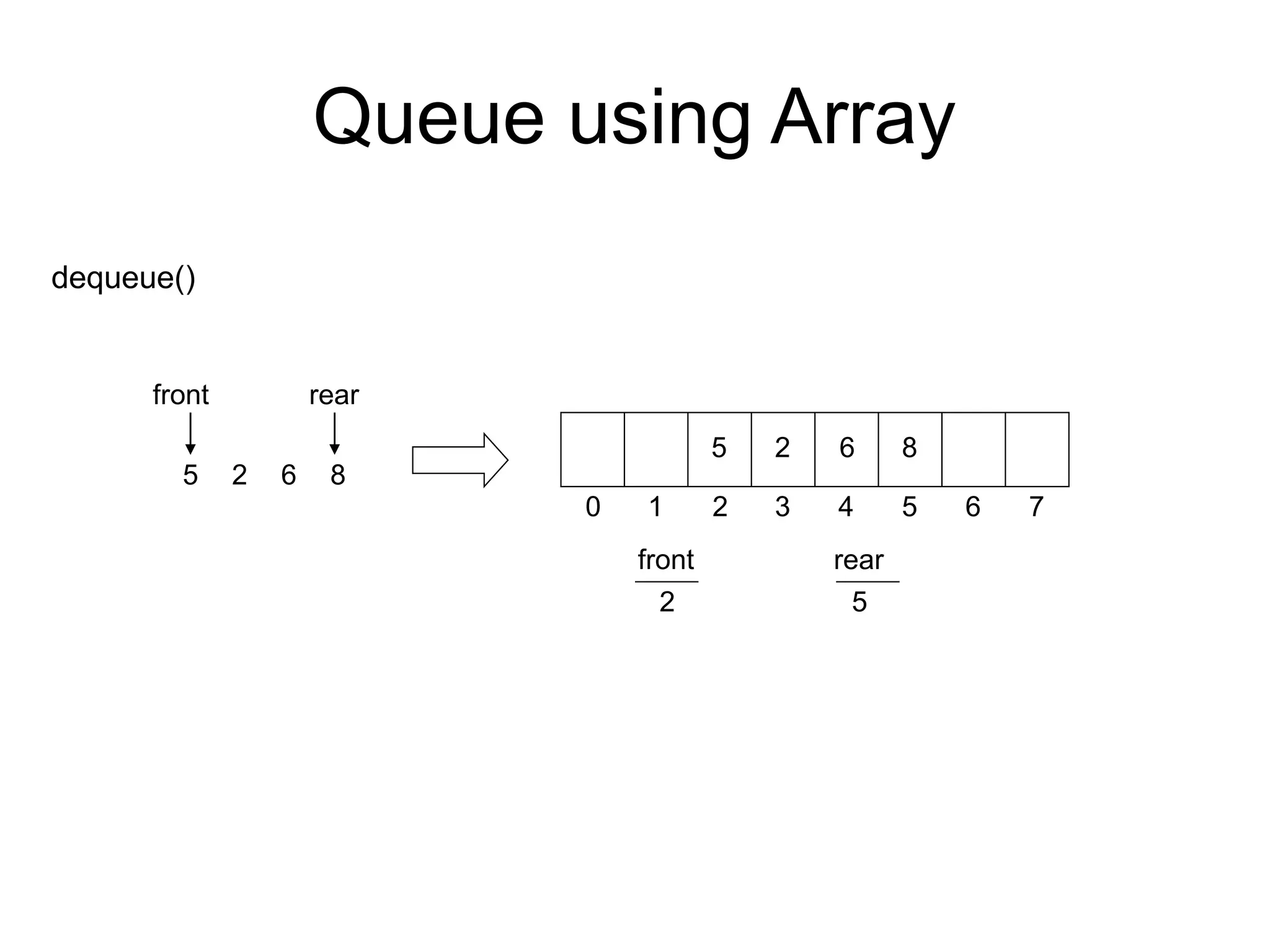
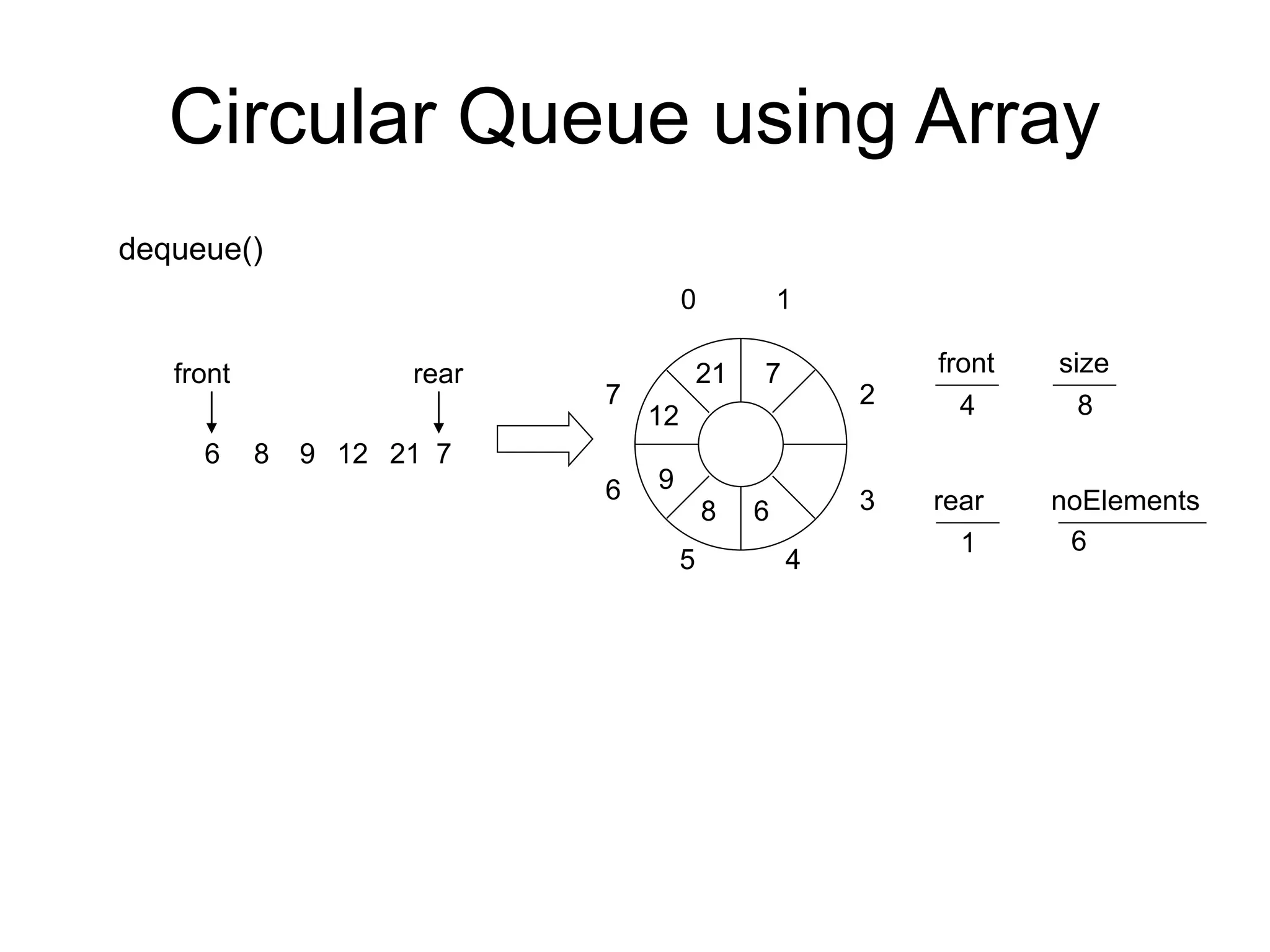
24. Deletion in Queue:
Algorithm: DEQUEUE(QUEUE, MAXSIZE, FRONT, REAR,COUNT, ITEM)
This procedure deletes an element from a queue and assigns it to the
variable ITEM.
1. [QUEUE already empty?]
If COUNT= 0 || FRONT==-1, then: Write: UNDERFLOW, and Return.
2. Set ITEM = QUEUE[FRONT].
3. Set COUNT = COUNT -1
4. [Find new value of FRONT.]
If COUNT = 0 || FRONT == REAR , then: [There was one element
remaining in queue and will be deleted, NOTE: FRONT and REAR are
not NULL]
Set FRONT= -1, and REAR = -1. [delete last element and
refresh queue to its initial position]
Else if FRONT= MAXSIZE-1, then: [queue is Circular!, so,]
Set FRONT = 0 [set Front = 0]
Else:
Set FRONT:=FRONT+1.
[End of If structure.]
5. Return ITEM

25. Following Figure shows that how a queue may be maintained by a circular array with
MAXSIZE = 6 (Six memory locations). Observe that queue always occupies
consecutive locations except when it occupies locations at the beginning and at the
end of the array. If the queue is viewed as a circular array, this means that it still
occupies consecutive locations. Also, as indicated by Fig(k), the queue will be empty
only when Count = 0 or (Front = Rear but not NULL) and an element is deleted. For
this reason, -1 (NULL) is assigned to Front and Rear.

28. , so set
Front = Max-1

29. CIRCULAR QUEUE

32. 32
Priority Queues

33. 33

34. 34

35. 35
• Think of a priority queue as a kind of bag that holds priorities.
You can put one in, and you can take out the
current highest priority. (Priorities can any Comparable values)
• A priority queue is different from a "normal" queue, because
instead of being a "first-in-first-out" data structure, values come
out in order by priority.
Here is a conceptual picture of a priority queue:

37. Not Quite Queues
• Consider applications
– ordering CPU jobs
– searching for the exit in a maze
– emergency room admission
processing
• Problems?
– short jobs should go first
– most promising nodes should be searched first
– most urgent cases should go first

38. Applications of the Priority Q
• Hold jobs for a printer in order of length
• Store packets on network routers in order of
urgency
• Sort numbers
• Simulate events
• Anything greedy

39. 39
• A priority queue might be used, for example, to handle the
jobs sent to the Computer Science Department's printer:
Jobs sent by the department chair should be printed first,
then jobs sent by professors, then those sent by graduate
students, and finally those sent by undergraduates.
• The values put into the priority queue would be the priority
of the sender (e.g., using 4 for the chair, 3 for professors,
2 for grad students, and 1 for undergrads), and the
associated information would be the document to print.
• Each time the printer is free, the job with the highest
priority would be removed from the print queue, and
printed. (Note that it is OK to have multiple jobs with the
same priority; if there is more than one job with the
same highest priority when the printer is free, then any
one of them can be selected.)
Priority queue

40. Priority Queue ADT
• Priority Queue operations
– create
– destroy
– insert
– deleteMin
– is_empty
• Priority Queue property: for two elements in
the queue, x and y, if x has a lower priority
value than y, x will be deleted before y
F(7) E(5)
D(100) A(4)
B(6)
insert deleteMin
G(9) C(3)

41. 41
Priority queue

43. 43
OPERATION DESCRIPTION
PriorityQ() (constructor) create an empty priority queue
boolean empty() return true iff the priority queue is empty
void insert(Comparable p) add priority p to the priority queue
Comparable removeMax()
remove and return the highest priority from the
priority queue (error if the priority queue is empty)
• The operations that need to be provided for a priority queue are
shown in the following table, assuming that just priorities (no
associated information) are to be stored in a priority queue.
• A priority queue can be implemented using many of the data
structures (an array, a linked list, or a binary search tree). However,
those data structures do not provide the most efficient operations. To
make all of the operations very efficient, we'll use a new data
structure called a heap.
Priority queue operations

44. 44
Priority queue: unordered and ordered
array implementation