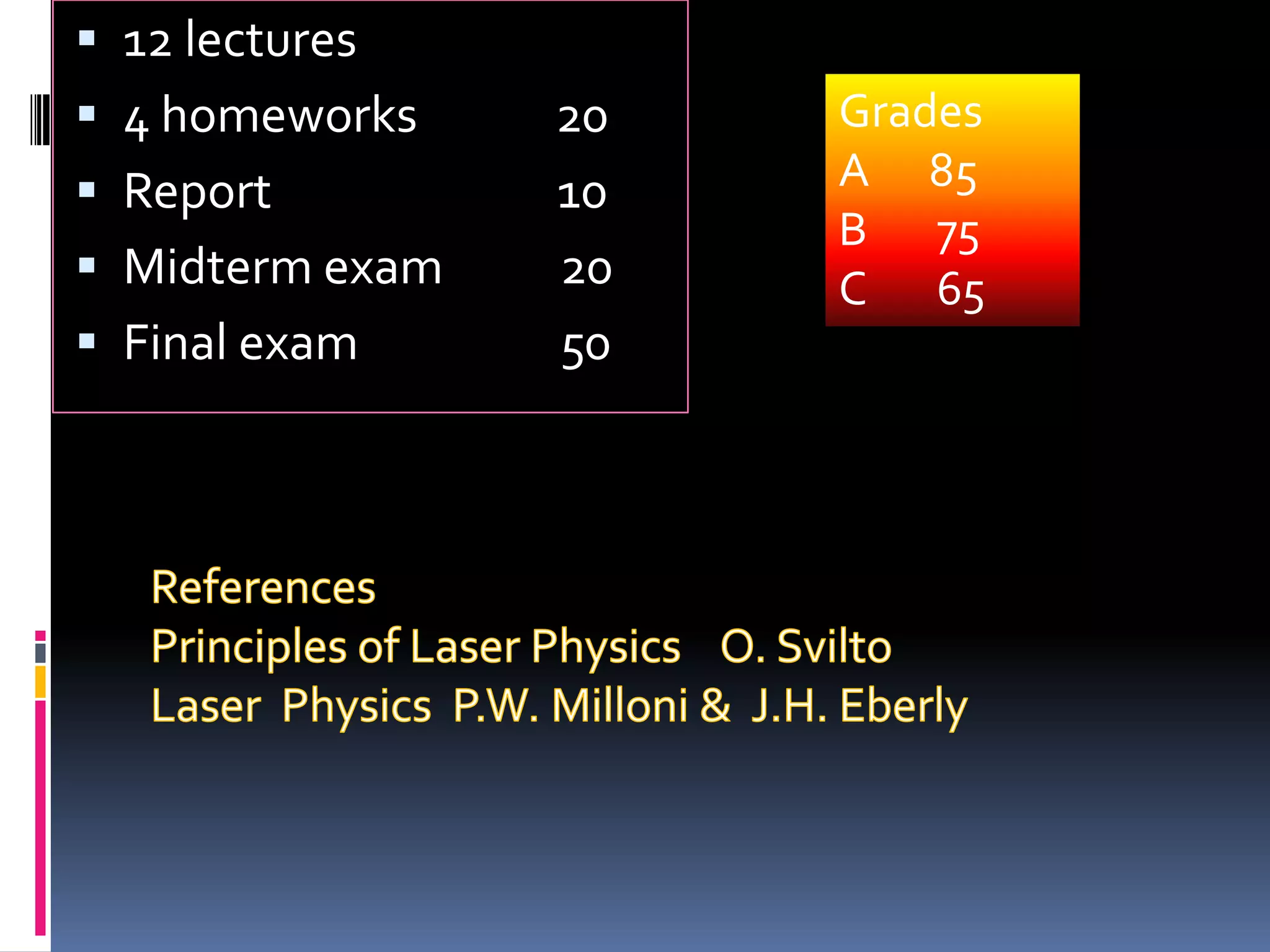
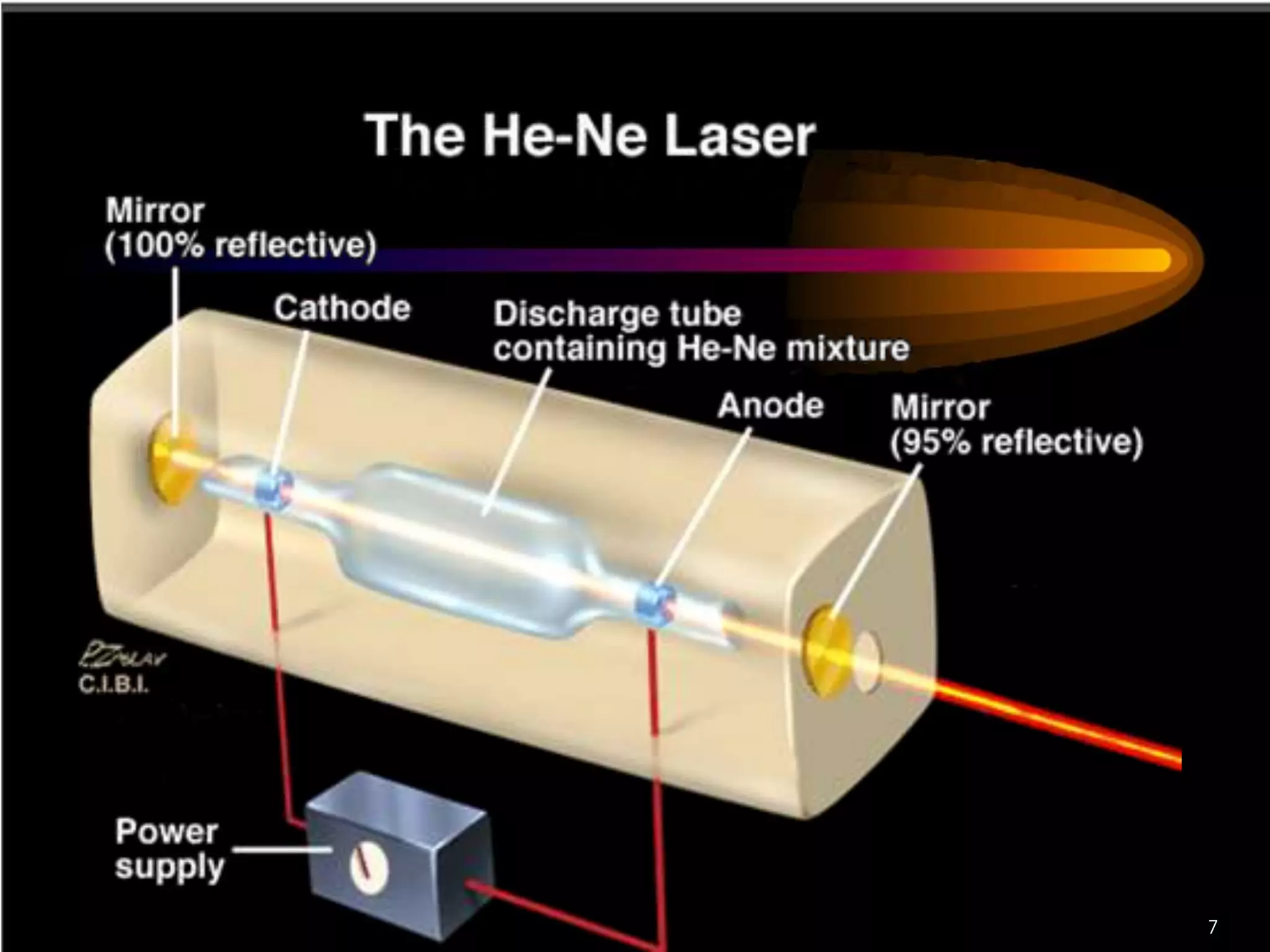
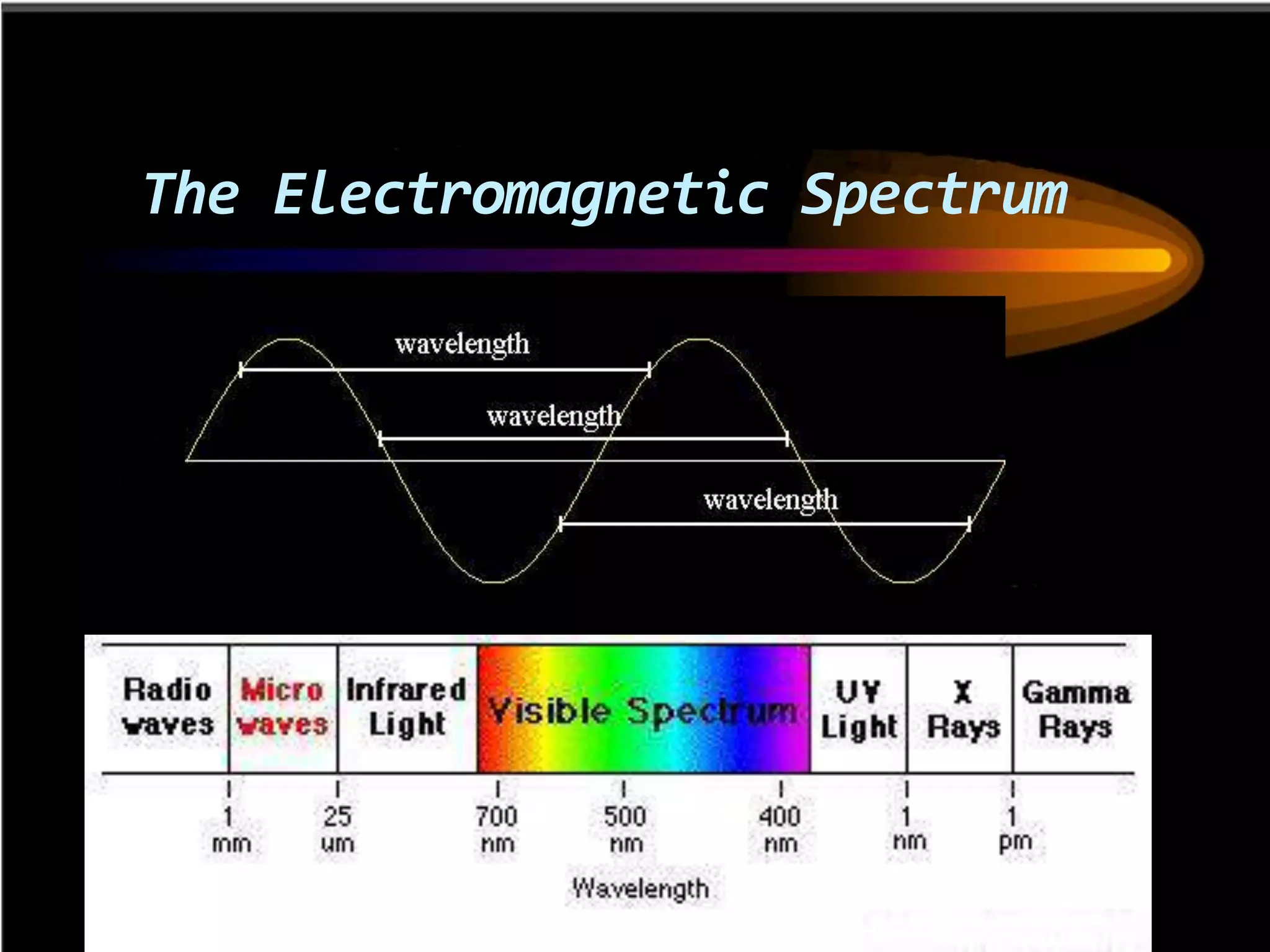
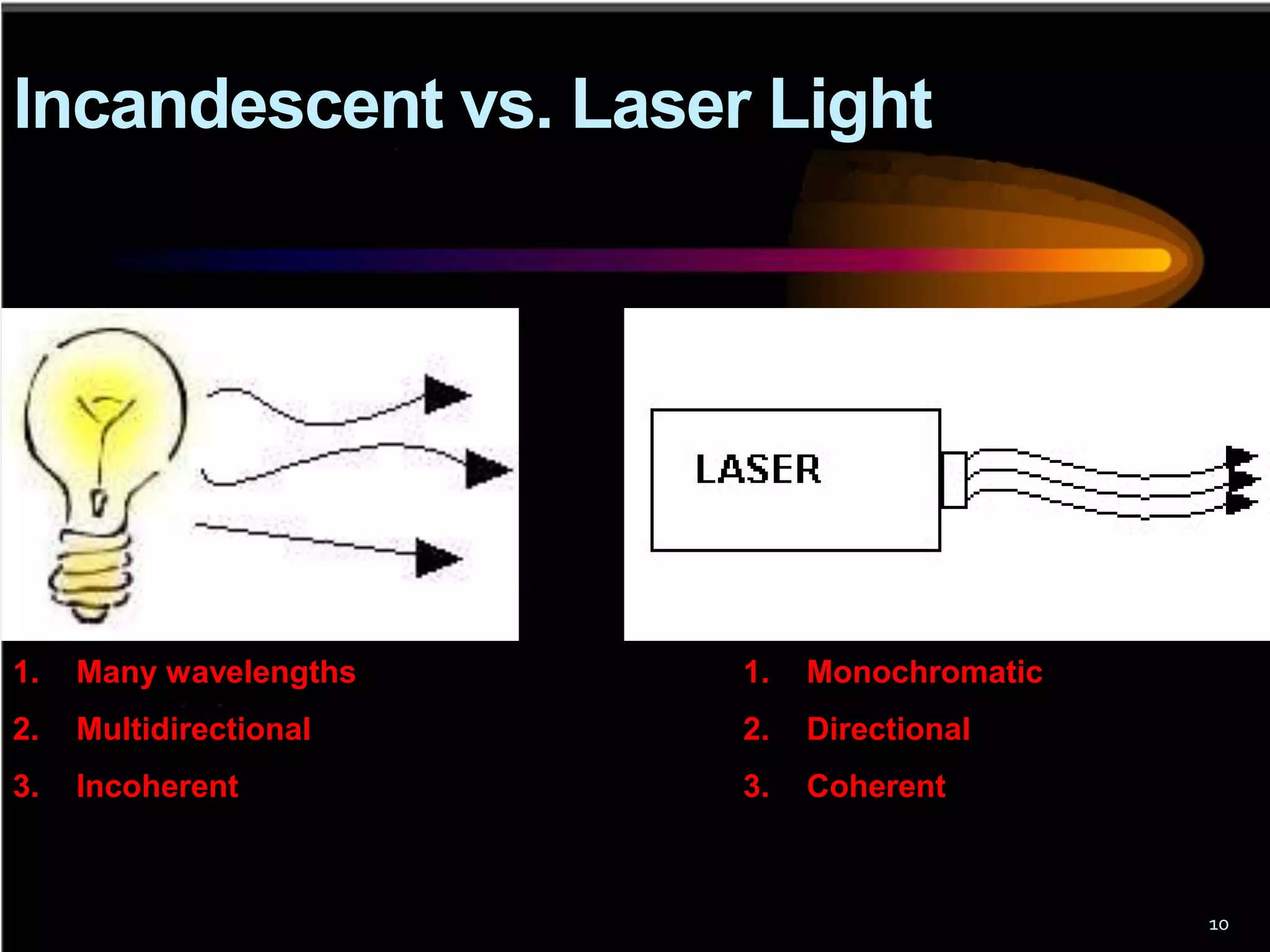
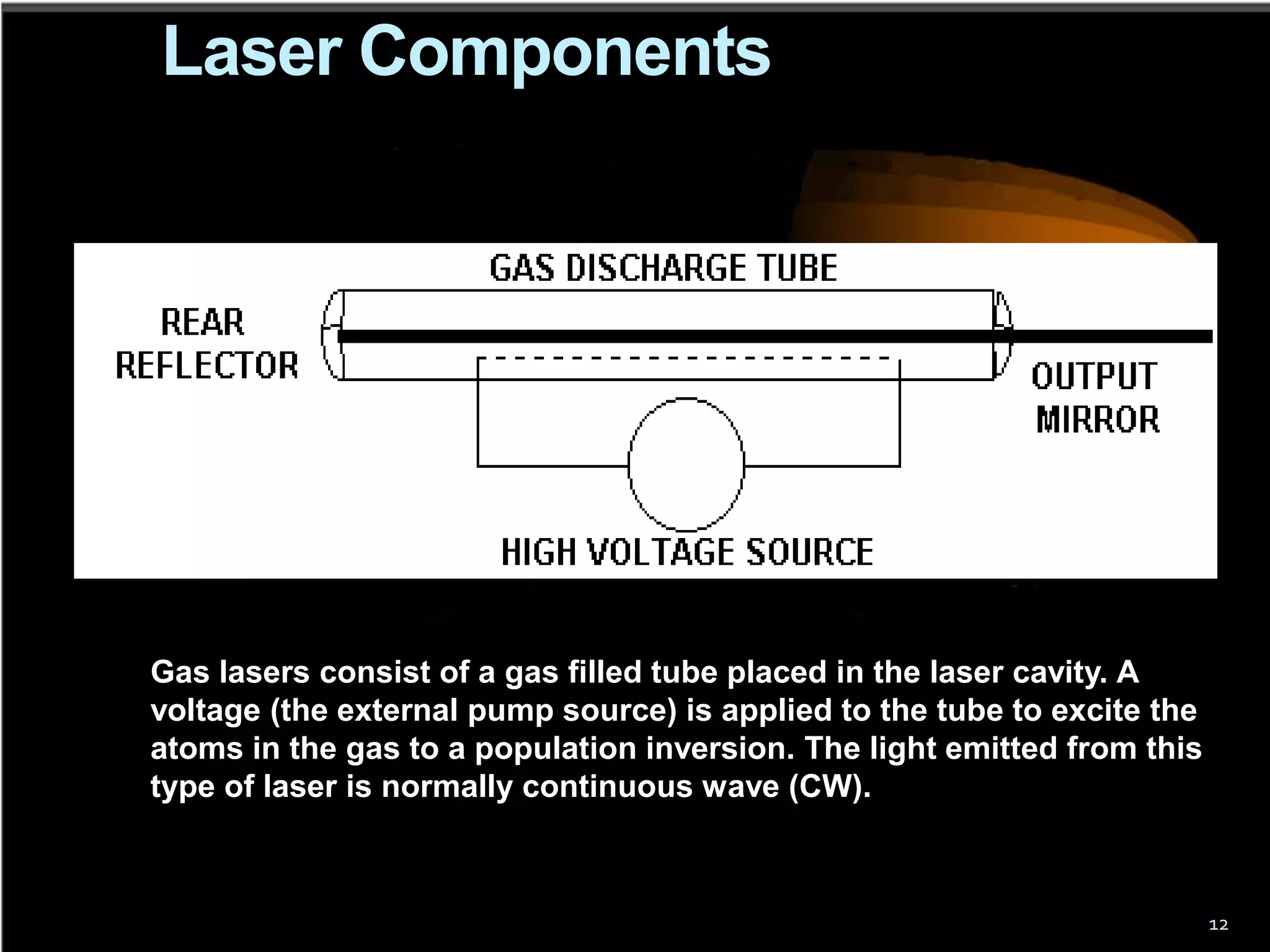
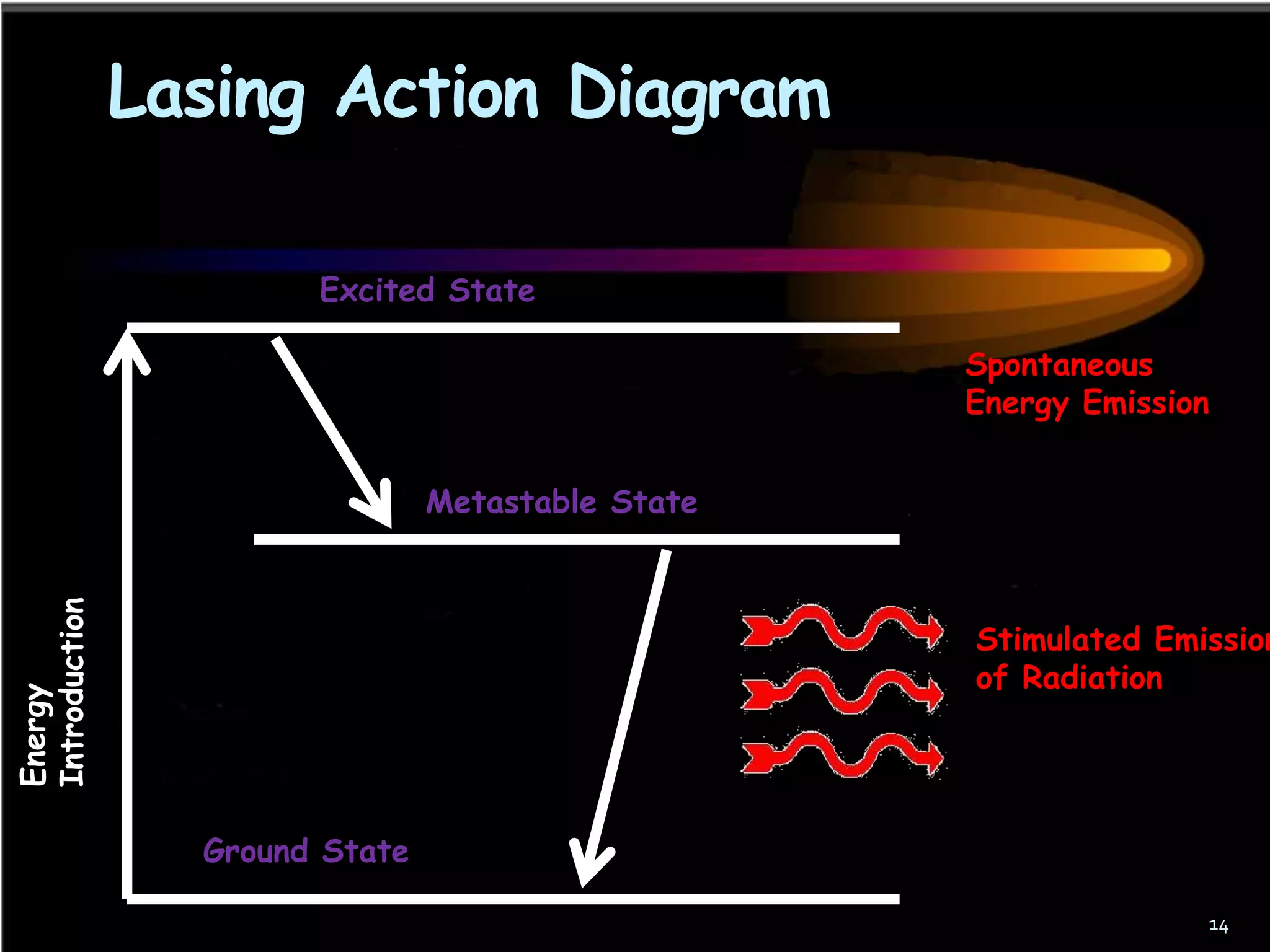
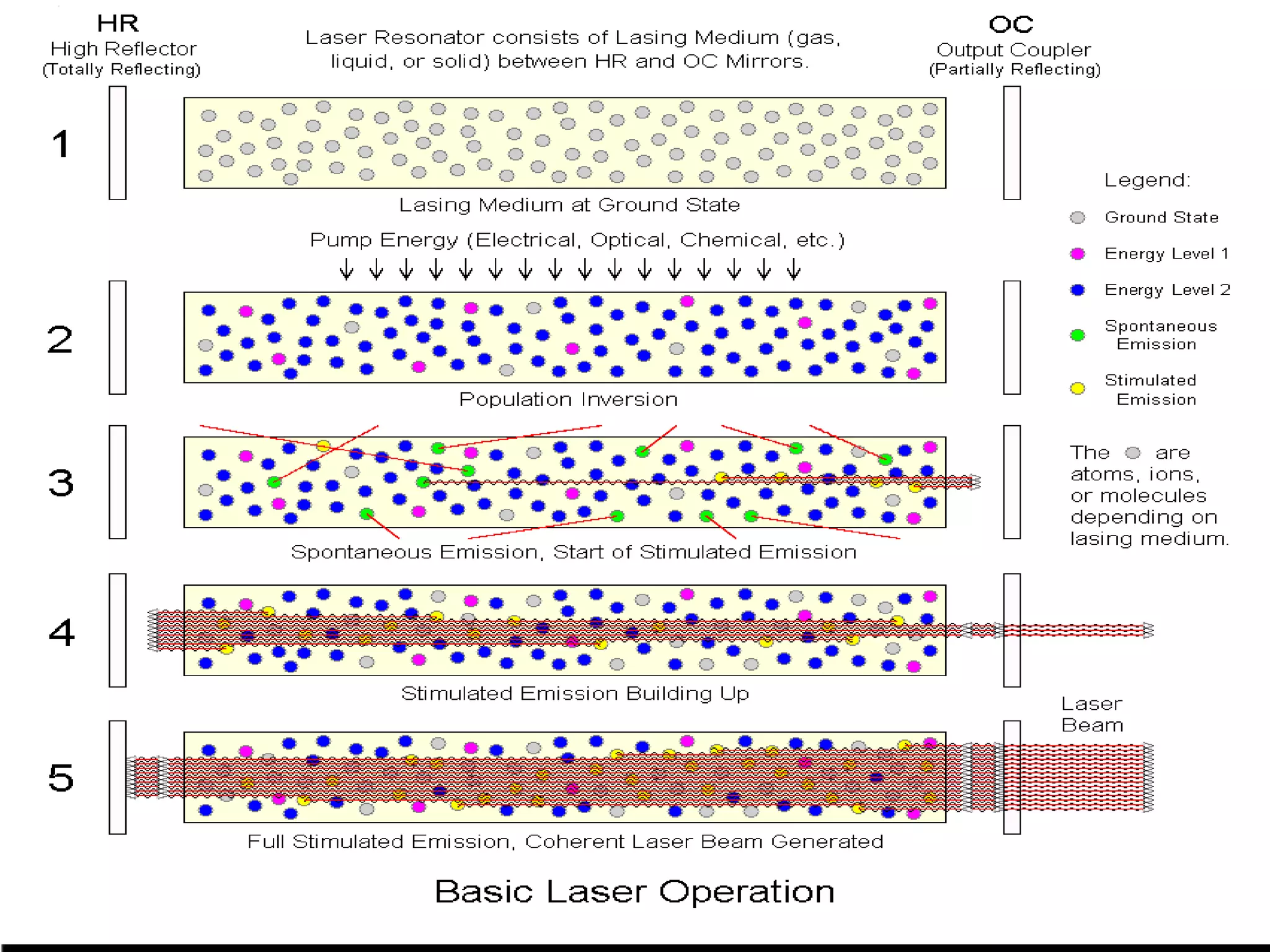
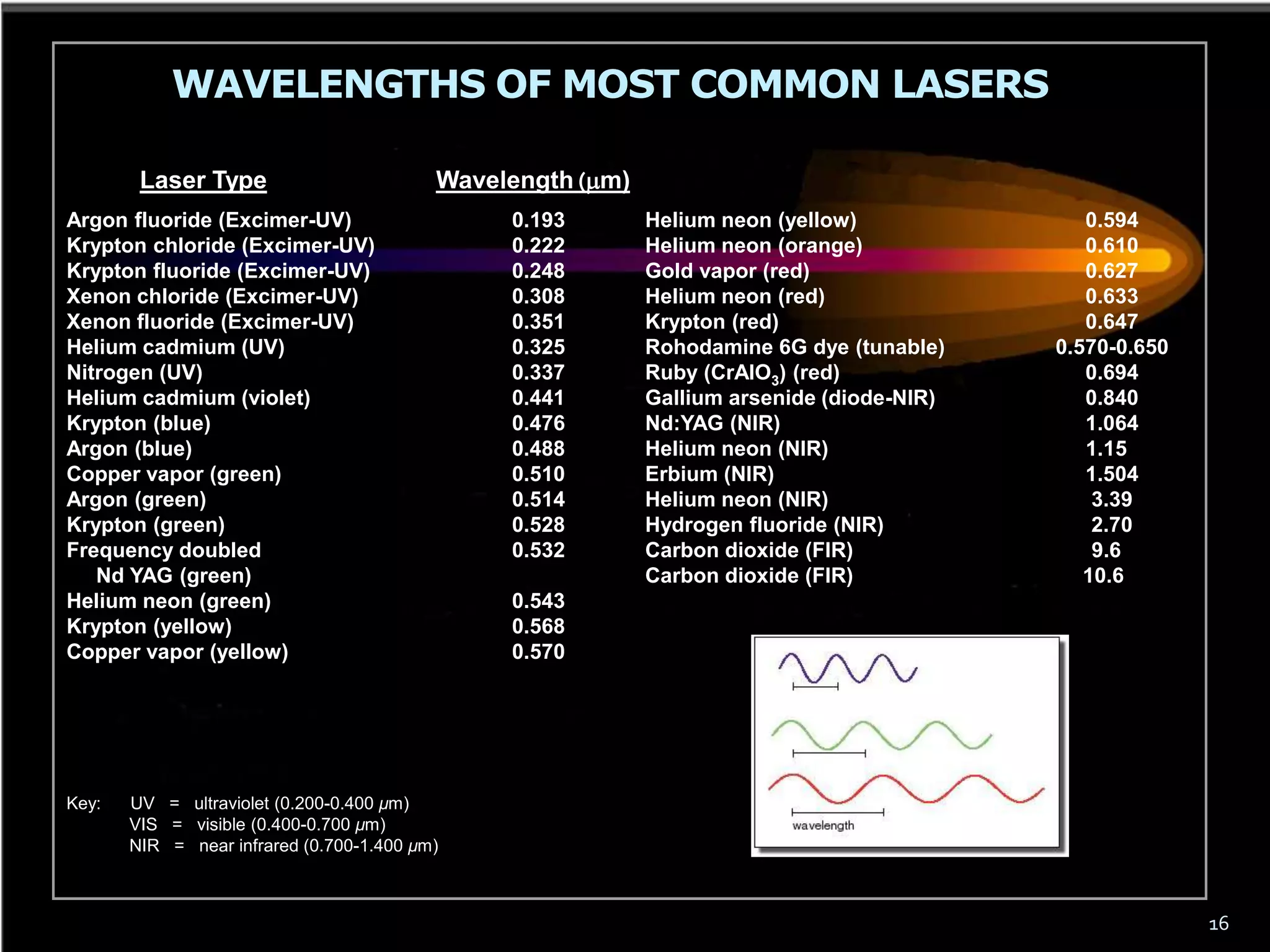
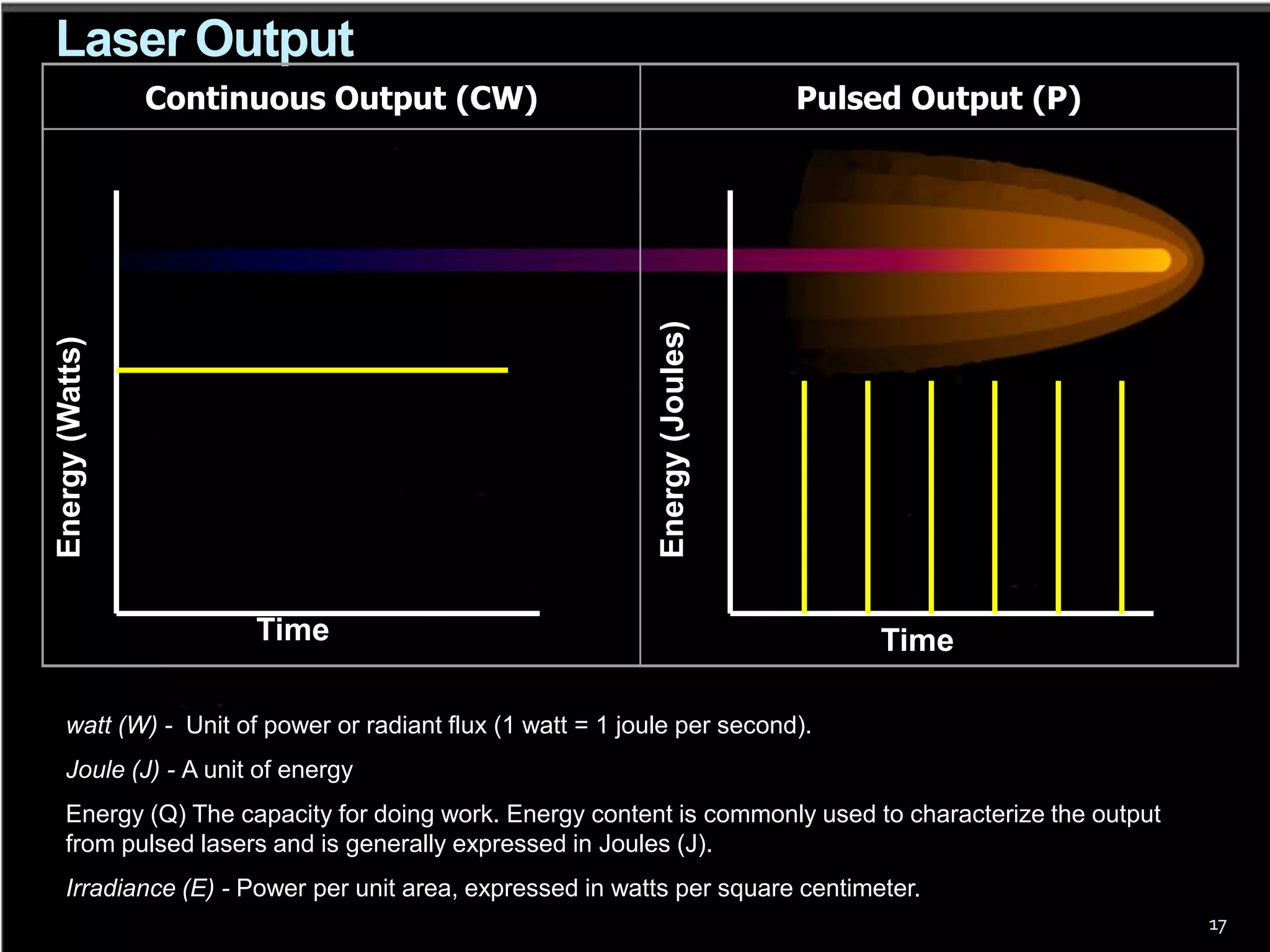
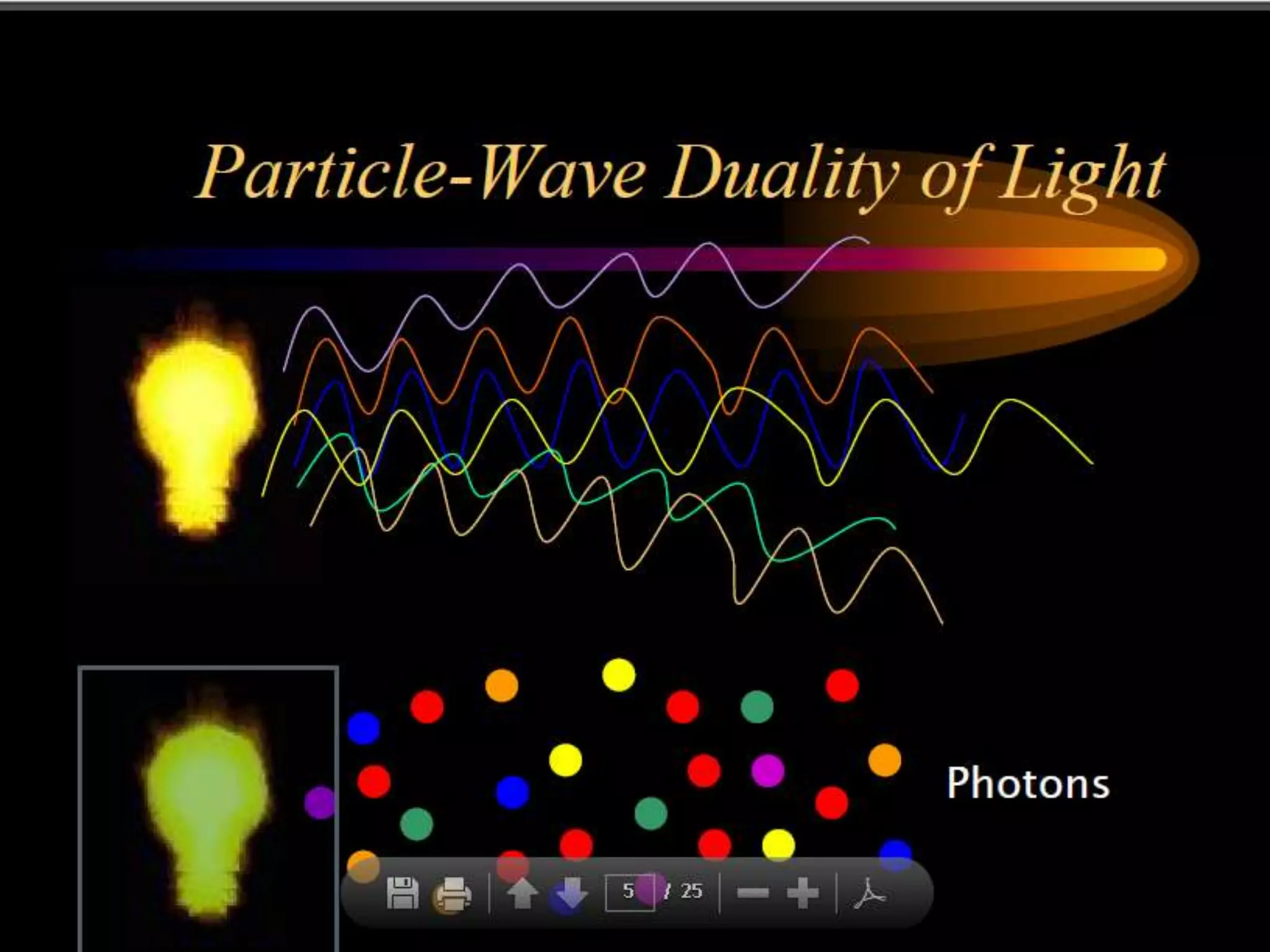
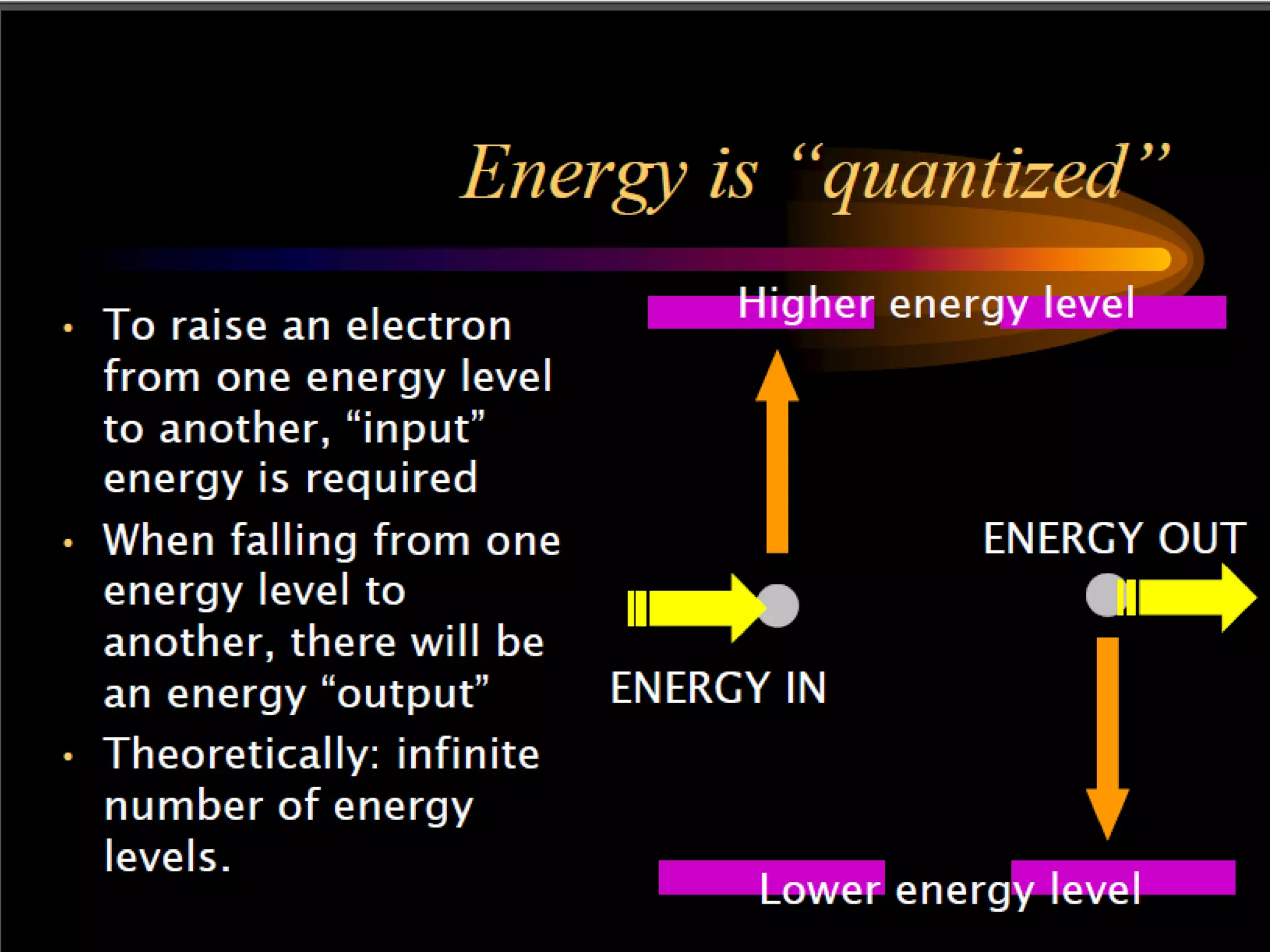
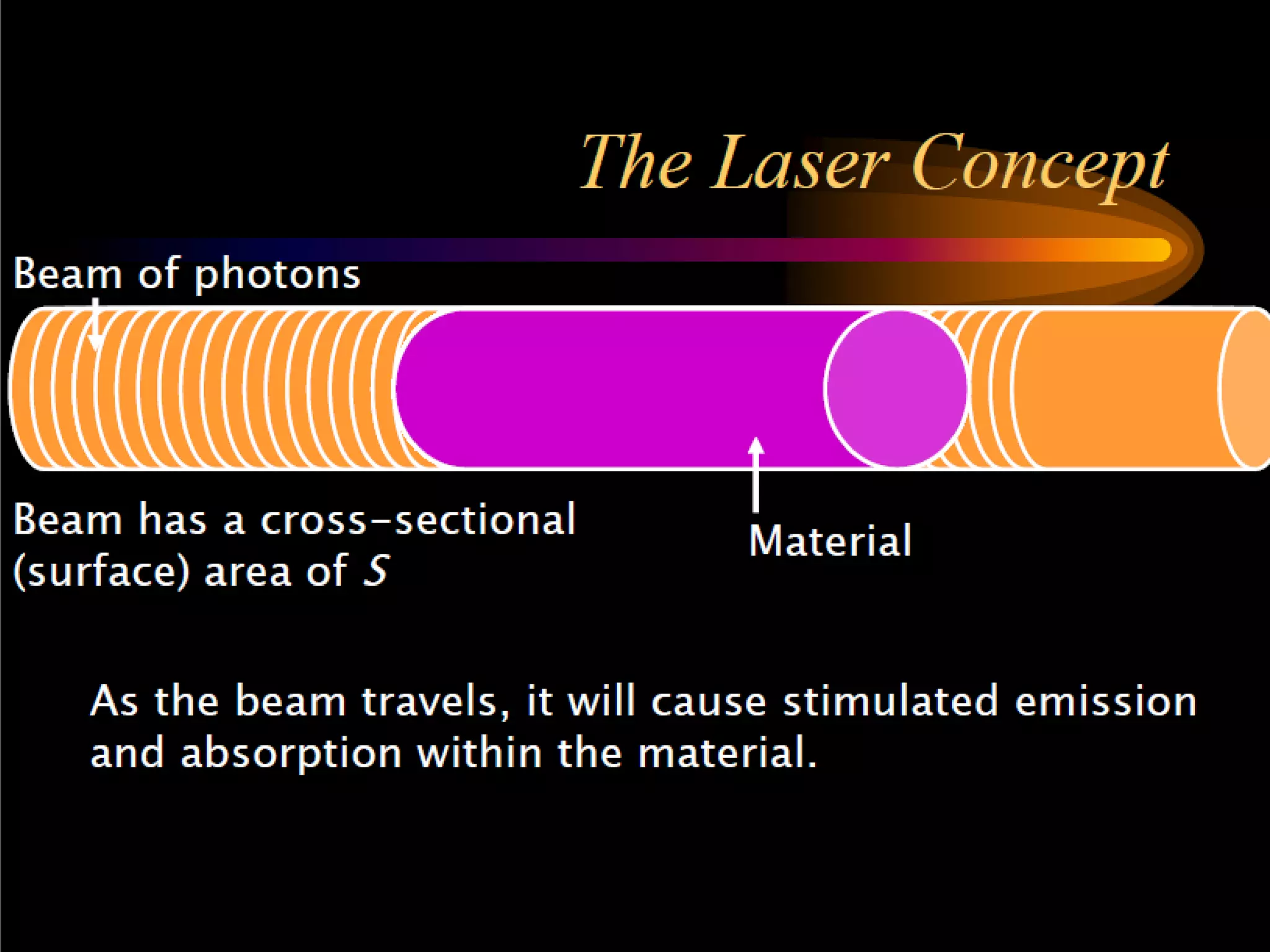
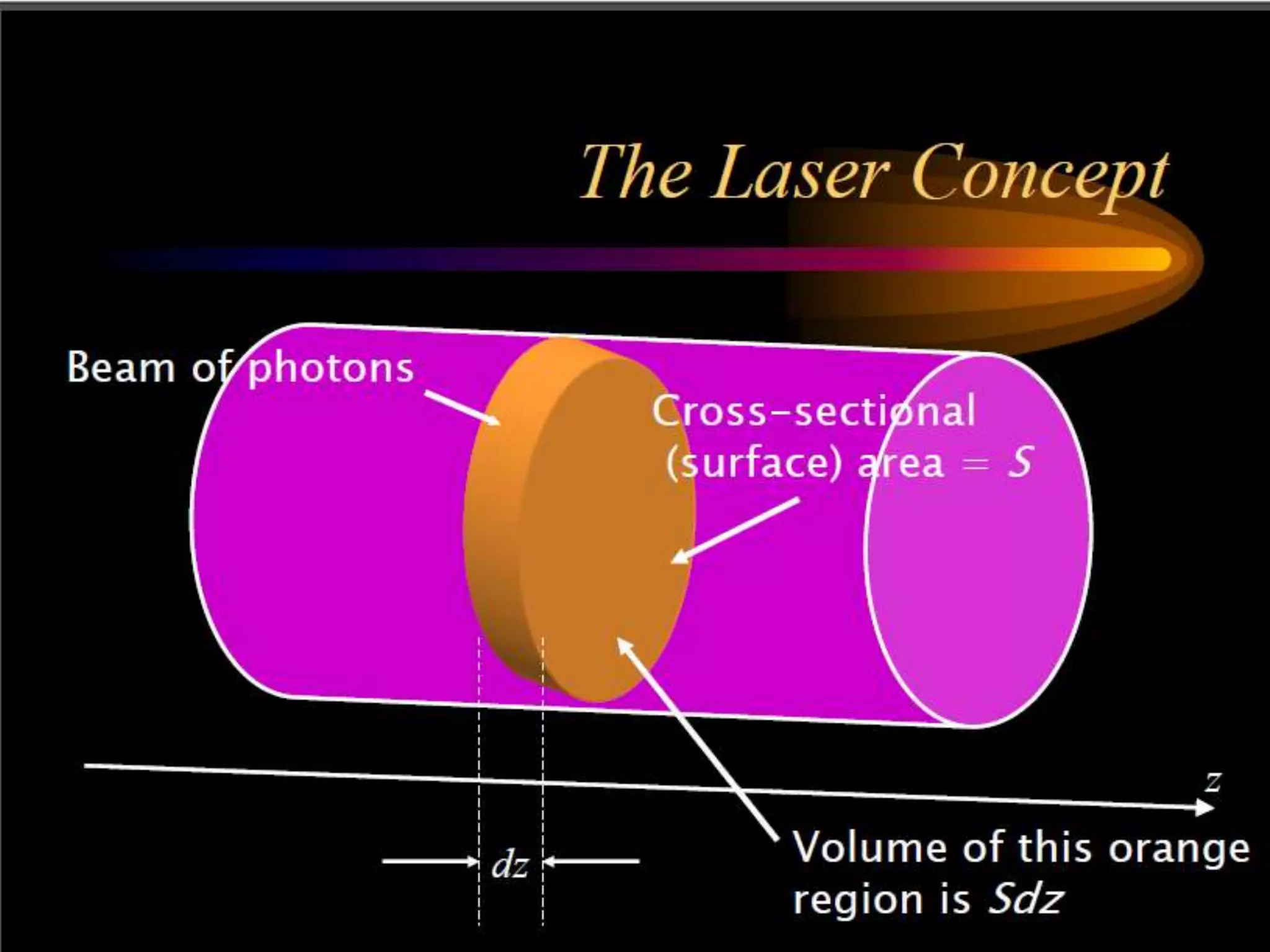
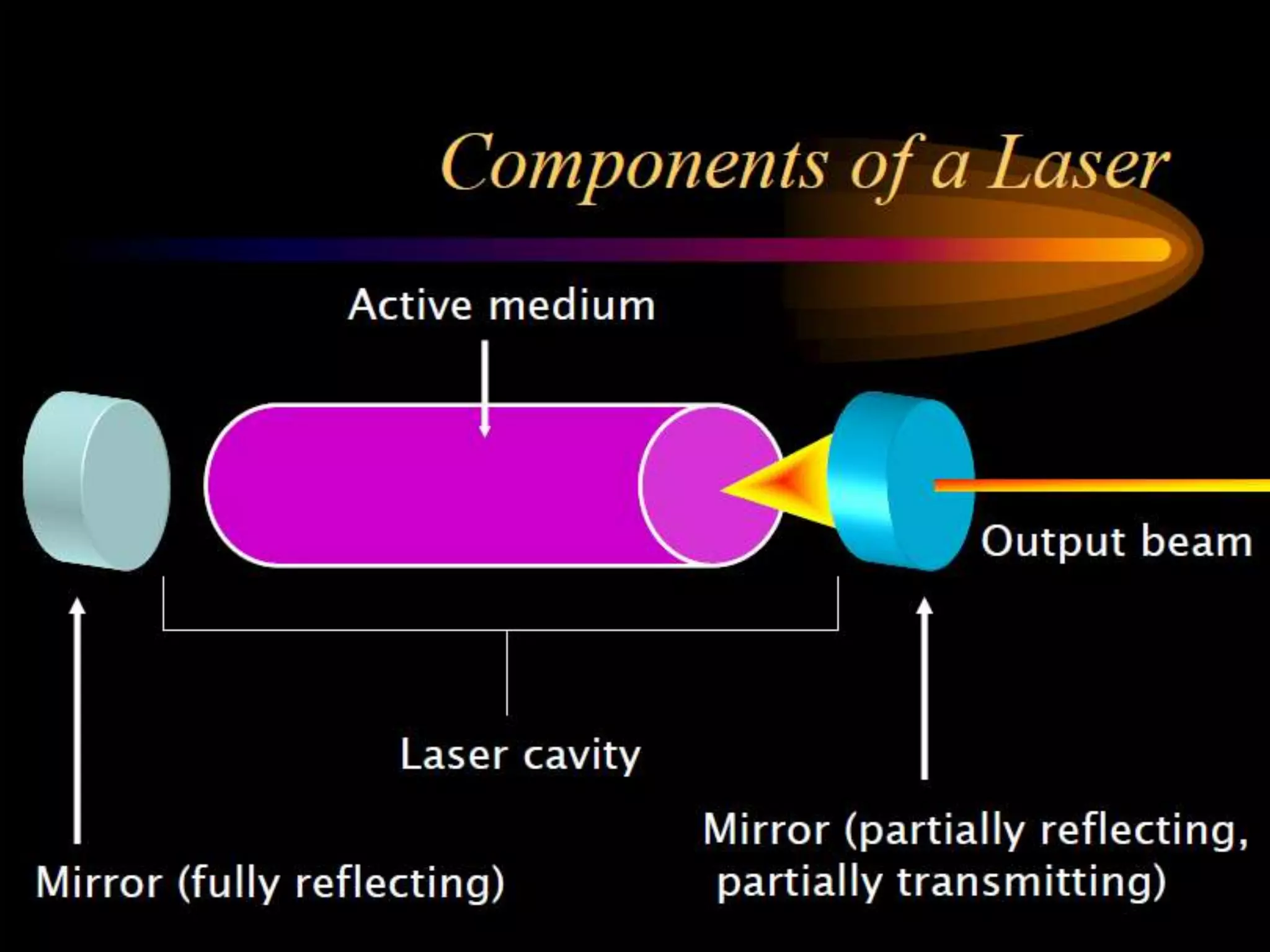
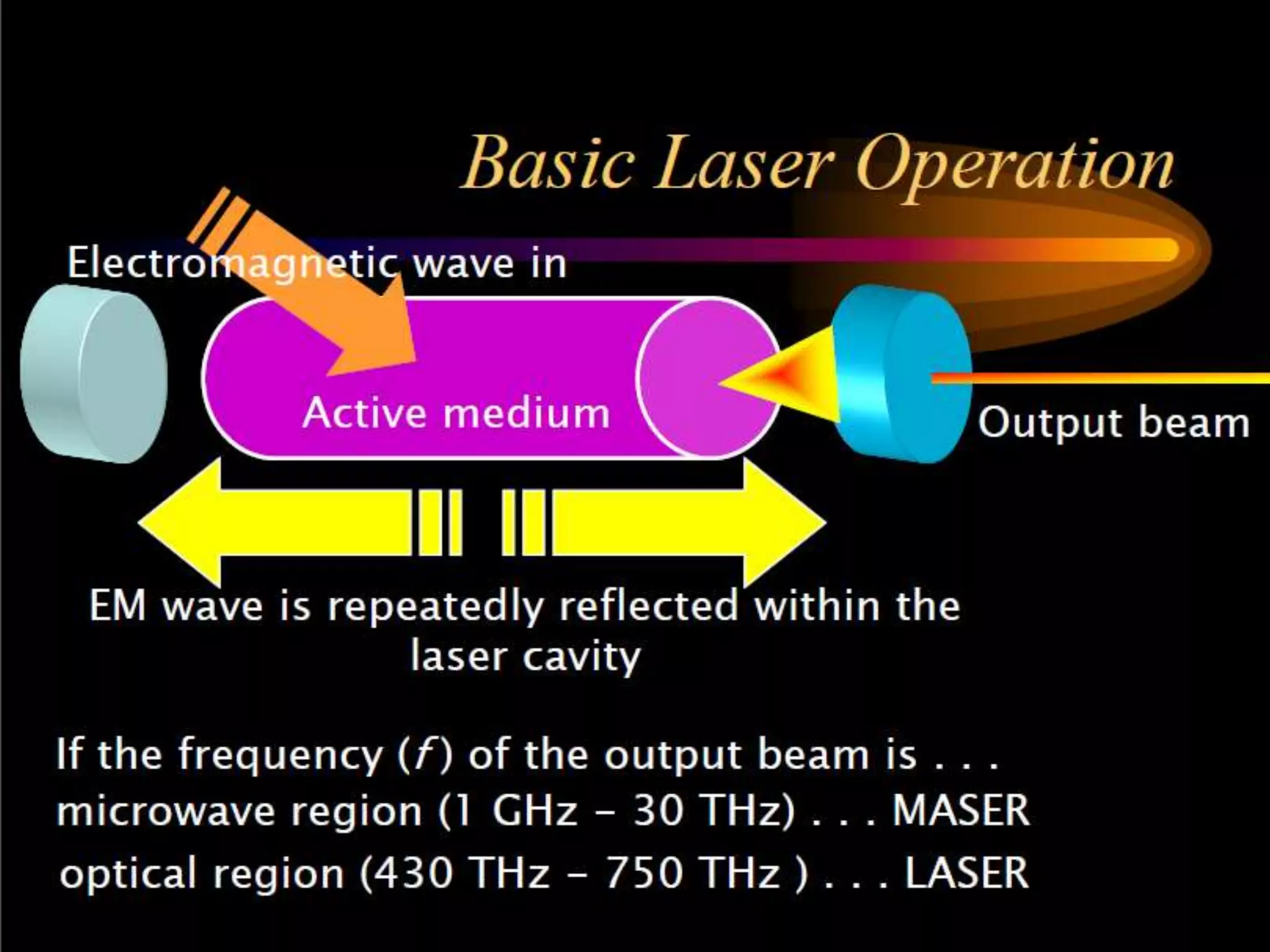
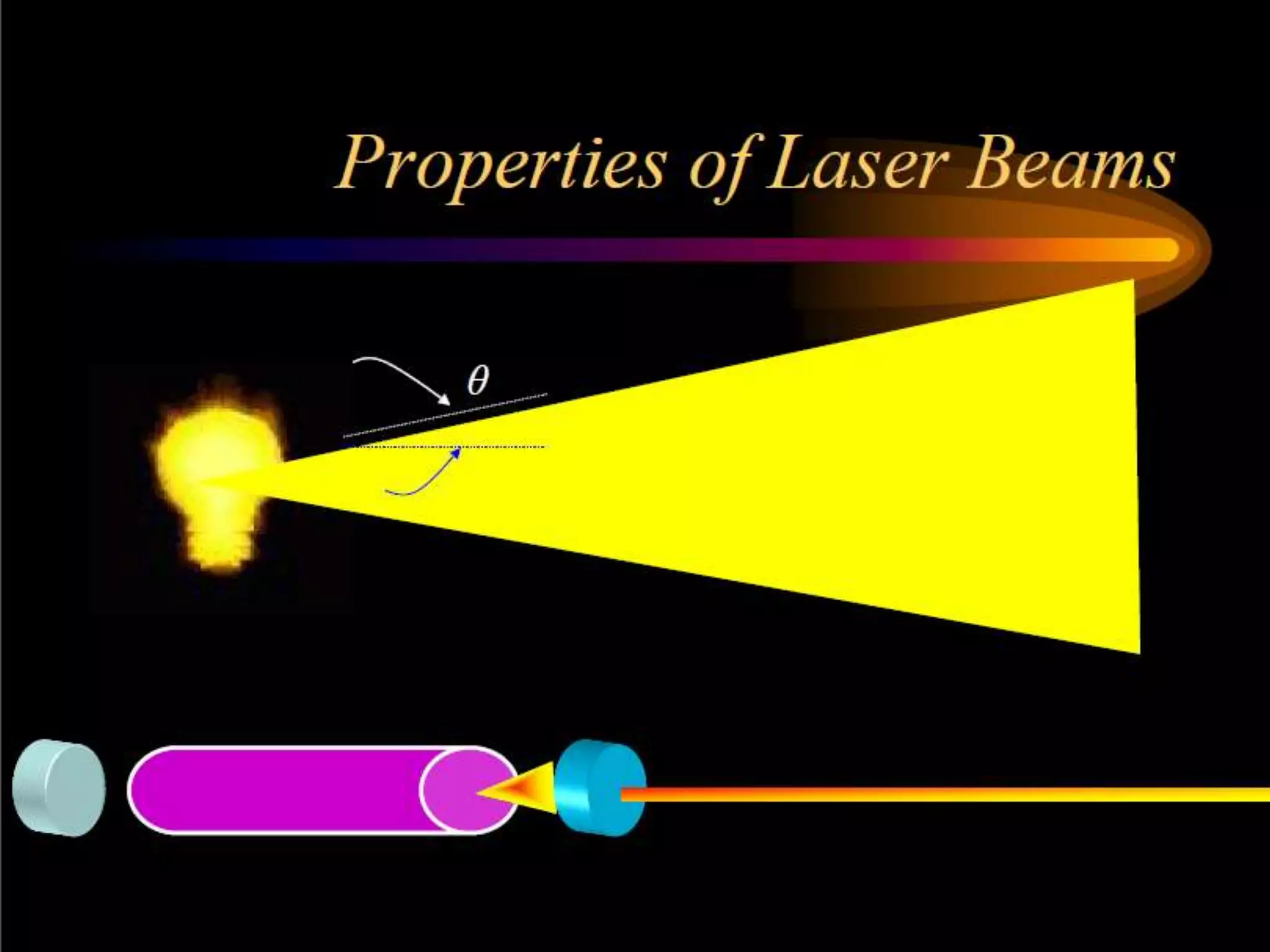
This document outlines the course structure and content for an introduction to laser theory class. The course will include 12 lectures, 4 homework assignments, a midterm exam, final exam, and individual reports. Key topics that will be covered include laser fundamentals, energy levels, rate equations, cavity design, gas lasers, solid state lasers, semiconductor lasers, and other laser types. Lasers can be classified based on their operation mode, population inversion mechanism, or active medium used. The goal is for students to understand the basic scientific principles that enable laser operation.

1. Prof. Dr. Salah Ibrahim Hassab Elnaby
Introduction to Laser Theory
Prof. Dr. Salah I. Hassab Elnaby
NILES

2.  12 lectures
 4 homeworks 20 Grades
 Report 10 A 85
B 75
 Midterm exam 20 C 65
 Final exam 50

3. Contents
 Introduction
 Energy Levels
 Absorption & Emission of Radiation
 Electro-Magnetic field
 Rate Equations
 Laser Cavity
 MID TERM EXAM
 CW and Pulsed operations
 Gas Lasers
 Solid State Lasers
 Semi-Conductor Lasers
 Other Types of Lasers (Free Electron & Liquid
Chemical)
 SIMINAR OF REPORTS

6. Types of Laser
Based on the mode of operation
(i) Pulsed Laser systems
(ii) High power Q-switched systems
(iii) Continuous wave Laser systems
Based on the mechanism in which Population
Inversion is achieved
(i) Three level lasers
(ii) Four level lasers
Based on state of active medium used
(i) Gas Laser
(ii) Solid state Laser
(iii) Semiconductor Laser
(iv) Tunable dye Laser

7. 7

8. The Electromagnetic Spectrum

9. Laser Fundamentals
 The light emitted from a laser is monochromatic, that
is, it is of one color/wavelength. In contrast, ordinary
white light is a combination of many colors (or
wavelengths) of light.
 Lasers emit light that is highly directional, that is, laser
light is emitted as a relatively narrow beam in a specific
direction. Ordinary light, such as from a light bulb, is
emitted in many directions away from the source.
 The light from a laser is said to be coherent, which
means that the wavelengths of the laser light are in
phase in space and time. Ordinary light can be a
mixture of many wavelengths.
These three properties of laser light are what can
make it more hazardous than ordinary light. Laser
light can deposit a lot of energy within a small area. 9

10. Incandescent vs. Laser Light
1. Many wavelengths 1. Monochromatic
2. Multidirectional 2. Directional
3. Incoherent 3. Coherent
10

11. Common Components of all Lasers
1. Active Medium
The active medium may be solid crystals such as ruby or Nd:YAG,
liquid dyes, gases like CO2 or Helium/Neon, or semiconductors
such as GaAs. Active mediums contain atoms whose electrons
may be excited to a metastable energy level by an energy source.
2. Excitation Mechanism
Excitation mechanisms pump energy into the active medium by
one or more of three basic methods; optical, electrical or
chemical.
3. High Reflectance Mirror
A mirror which reflects essentially 100% of the laser light.
4. Partially Transmissive Mirror
A mirror which reflects less than 100% of the laser light and
transmits the remainder.
11

12. Laser Components
Gas lasers consist of a gas filled tube placed in the laser cavity. A
voltage (the external pump source) is applied to the tube to excite the
atoms in the gas to a population inversion. The light emitted from this
type of laser is normally continuous wave (CW).
12

13. Lasing Action
1. Energy is applied to a medium raising electrons to an unstable
energy level.
2. These atoms spontaneously decay to a relatively long-lived, lower
energy, metastable state.
3. A population inversion is achieved when the majority of atoms have
reached this metastable state.
4. Lasing action occurs when an electron spontaneously returns to its
ground state and produces a photon.
5. If the energy from this photon is of the precise wavelength, it will
stimulate the production of another photon of the same wavelength
and resulting in a cascading effect.
6. The highly reflective mirror and partially reflective mirror continue
the reaction by directing photons back through the medium along
the long axis of the laser.
7. The partially reflective mirror allows the transmission of a small
amount of coherent radiation that we observe as the “beam”.
8. Laser radiation will continue as long as energy is applied to the
lasing medium.
13

14. Lasing Action Diagram
Excited State
Spontaneous
Energy Emission
Metastable State
Introduction
Stimulated Emission
of Radiation
Energy
Ground State
14

15. 15

16. WAVELENGTHS OF MOST COMMON LASERS
Laser Type Wavelength (mm)
Argon fluoride (Excimer-UV) 0.193 Helium neon (yellow) 0.594
Krypton chloride (Excimer-UV) 0.222 Helium neon (orange) 0.610
Krypton fluoride (Excimer-UV) 0.248 Gold vapor (red) 0.627
Xenon chloride (Excimer-UV) 0.308 Helium neon (red) 0.633
Xenon fluoride (Excimer-UV) 0.351 Krypton (red) 0.647
Helium cadmium (UV) 0.325 Rohodamine 6G dye (tunable) 0.570-0.650
Nitrogen (UV) 0.337 Ruby (CrAlO3) (red) 0.694
Helium cadmium (violet) 0.441 Gallium arsenide (diode-NIR) 0.840
Krypton (blue) 0.476 Nd:YAG (NIR) 1.064
Argon (blue) 0.488 Helium neon (NIR) 1.15
Copper vapor (green) 0.510 Erbium (NIR) 1.504
Argon (green) 0.514 Helium neon (NIR) 3.39
Krypton (green) 0.528 Hydrogen fluoride (NIR) 2.70
Frequency doubled 0.532 Carbon dioxide (FIR) 9.6
Nd YAG (green) Carbon dioxide (FIR) 10.6
Helium neon (green) 0.543
Krypton (yellow) 0.568
Copper vapor (yellow) 0.570
Key: UV = ultraviolet (0.200-0.400 µm)
VIS = visible (0.400-0.700 µm)
NIR = near infrared (0.700-1.400 µm)
16

17. Laser Output
Continuous Output (CW) Pulsed Output (P)
Energy (Joules)
Energy (Watts)
Time Time
watt (W) - Unit of power or radiant flux (1 watt = 1 joule per second).
Joule (J) - A unit of energy
Energy (Q) The capacity for doing work. Energy content is commonly used to characterize the output
from pulsed lasers and is generally expressed in Joules (J).
Irradiance (E) - Power per unit area, expressed in watts per square centimeter.
17

24. Photon Energy
The energy of a green–yellow photon, roughly in
the middle of the optical spectrum, has an energy
of about 2.5 eV (electron volts). This is the same as
about 4x10-19 J ( joules)= 4x10-12 erg.
From the infrared to the X-ray region photon
energies vary from about 0.01 eV to about 100 eV.
For contrast, at room temperature the thermal unit
of energy is kT ~ 1/40 eV =0:025 eV. This is two
orders of magnitude smaller than the typical
optical photon energy just mentioned, and as a
consequence thermal excitation plays only a very
small role in the physics of nearly all lasers.

25. Directionality
The output of a laser can consist of nearly ideal plane
wavefronts. Only diffraction imposes a lower limit on
on the angular spread of a laser beam the beam’s solid
angle (ΔΩ) and vertex angle (Δθ) of divergence
ΔΩ = λ2/A =(Δθ)2
This represents a very small angular spread indeed if
λ is in the optical range, say
500 nm, and A is macroscopic, say (5 mm)2.
In this example we compute
ΔΩ = (500)210-18 m2/(5x10-6 m2) = 10-8 sr,
Δθ = 1/10 mrad.

26. Coherence Time
The existence of a finite bandwidth Δν means that the
different frequencies present in a laser beam can eventually
get out of phase with each other.
The time required for two oscillations differing in frequency
by Δν to get out of phase by a full cycle is obviously 1/ Δν.
After this amount of time the different frequency
components in the beam can begin to interfere destructively,
and the beam loses “coherence.”
Thus,
Δt = 1/ Δν is called the beam’s coherence time.

27. For example, even a “broadband” laser with Δν ~ 1 MHz has
the coherence time Δt ~ 1 ms. This is enormously longer than
most “typical” atomic fluorescence lifetimes, which are
measured in nanoseconds (10-9 s).
Thus even lasers that are not close to the limit of spectral
purity are nevertheless effectively 100% pure on the relevant
spectroscopic time scale.
By way of contrast, sunlight has a bandwidth Δν almost as
great as its central frequency (yellow light, ν= 5x1014 Hz).
Thus, for sunlight the coherence time is Δt~ 2x10-15 s, so
short that unfiltered sunlight cannot be considered
temporally coherent at all.

28. Coherence Length
The speed of light is so great that a light beam can travel a
very great distance within even a short coherence time. For
example, within Δt 1 ms light travels Δz ~300 m.
The distance Δz= c Δt is called the beam’s coherence
length. Only portions of the same beam that are separated
by less than Δz are capable of
interfering constructively with each other.

29. Spectral Brightness
A light beam from a finite source can be characterized by its
beam divergence ΔΩ, source size (usually surface area A),
bandwidth Δν, and spectral power density Pν
(watts per hertz of bandwidth). From these parameters it is
useful to determine the spectral brightness βν of the source,
which is defined to be the power flow per unit area, unit
bandwidth, and steradian, namely
βν= Pν/A ΔΩΔν.

30. Notice that Pν/A Δν is the spectral intensity, so βν can also be
thought of as the spectral intensity per steradian.
For an ordinary nonlaser optical source, brightness can be
estimated directly from the blackbody formula for ρ(ν), the
spectral energy density (J/m3-Hz):
The spectral intensity (W/m2-Hz) is thus cρr, and c ρ /Δν is
the desired spectral intensity per steradian. Taking Δν= 4p
for a blackbody, we have

31. The temperature of the sun is about T=5800K 20(300K).
Since the main solar
emission is in the yellow portion of the spectrum, we can
take hν= 2.5 eV.
βν= 1.5 x10-8 W/m2-sr-Hz for the sun
Several different estimates can be made for laser radiation,
depending on the type of laser
considered. Consider first a low-power He–Ne laser. A power
level of 1 mWis normal,
with a bandwidth of around 104 Hz. That the product of
beam
cross-sectional area and solid angle is just λ2, which for He–
Ne light λ2(6328 x10-10 m)2. Combining these, we find
βν =2:5 105W=m2-sr-Hz (He–Ne laser):

32. Another common laser is the mode-locked neodymium–
glass laser, which can easily reach power levels around 104
MW. The bandwidth of such a laser is limited by the
pulse duration, say tp 30 ps (3010212 s). The bandwidth is
greater than 1/tp 3.3x1010 s-1. We convert from radians per
second to cycles per second by dividing
by 2π and get Δν = 5x109 Hz.
The wavelength of a Nd : glass laser is 1.06 μm, so λ2 =10-12
m2.
The result of combining these,
Βν= 2x 1012 W/m2-sr-Hz (Nd : glass laser):