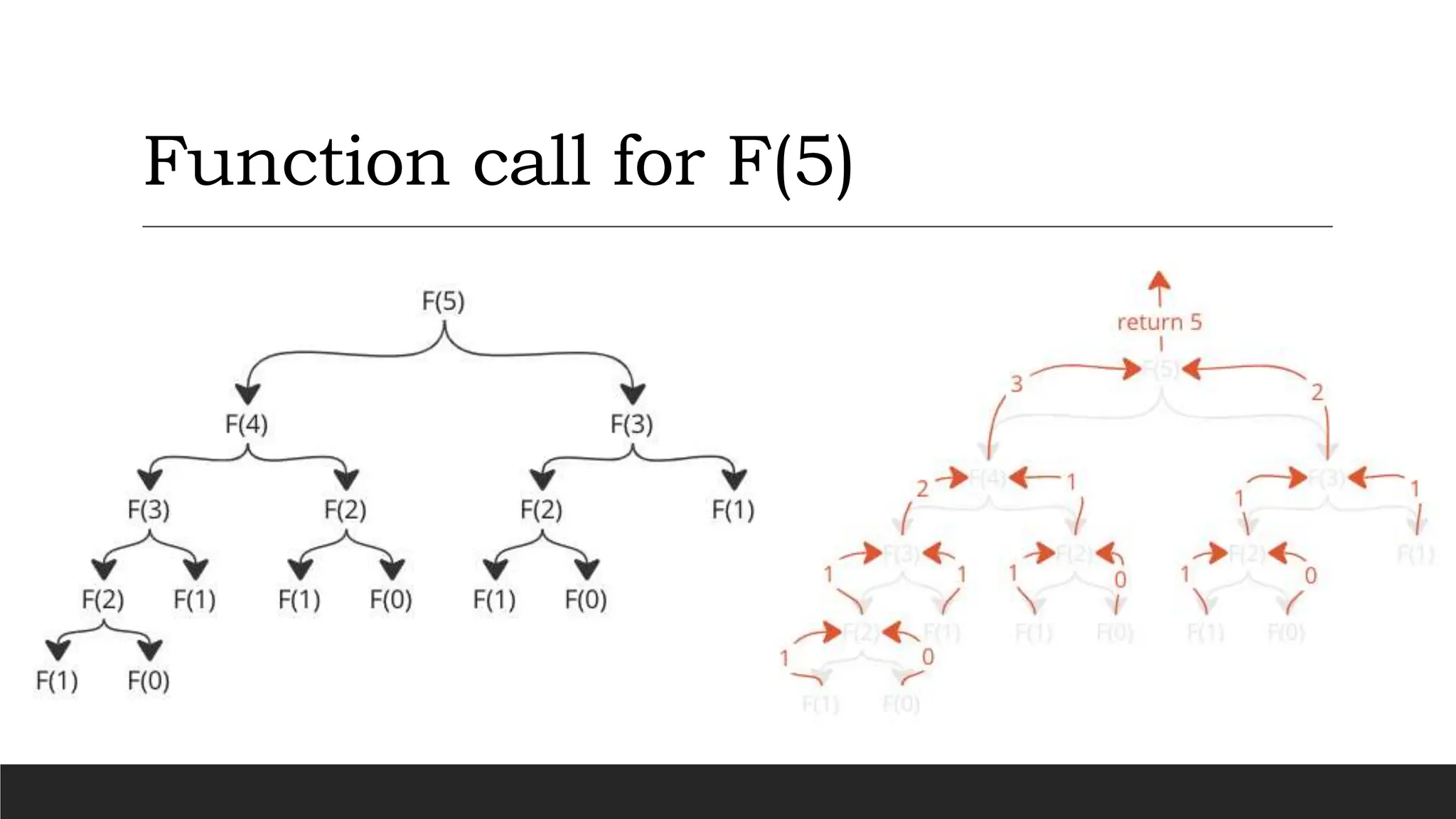
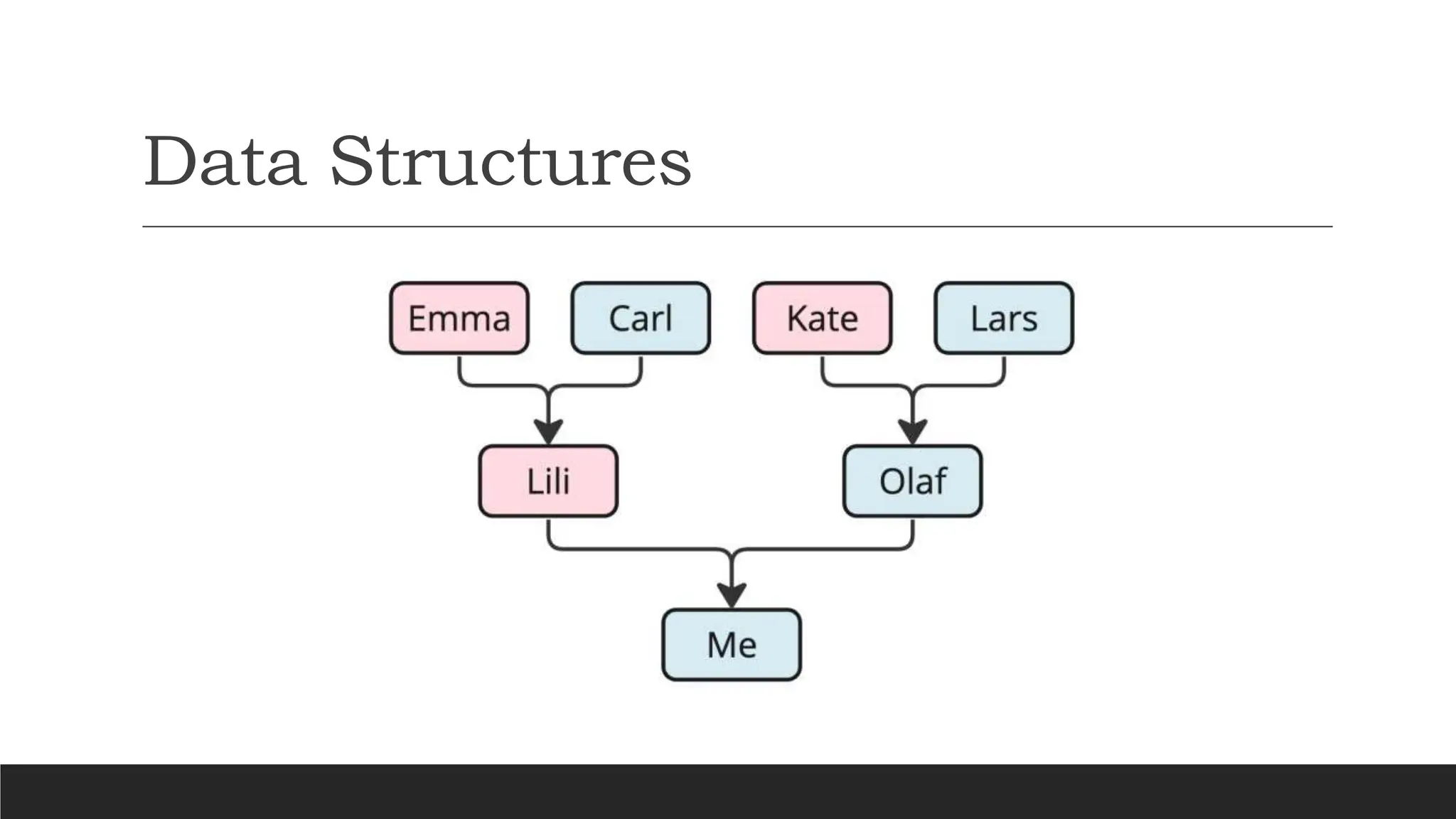
The document explains data structures and algorithms (DSA), highlighting their importance in efficiently storing and manipulating large amounts of data for various applications, such as operating systems and web applications. It details the two types of data structures (primitive and abstract) and provides examples of algorithms, including the Fibonacci sequence, and discusses their implementation using loops and recursion. Understanding DSA is crucial for solving complex problems and improving program efficiency.























![Java
public class Main {
public static void main(String[] args) {
int prev2 = 0;
int prev1 = 1;
System.out.println(prev2);
System.out.println(prev1);
for(int fibo = 0; fibo < 18; fibo++) {
int newFibo = prev1 + prev2;
System.out.println(newFibo);
prev2 = prev1;
prev1 = newFibo;
}
}
}](https://image.slidesharecdn.com/l1-introduction-240616033220-d2d24db9/75/L1-Introduction-for-Computer-Science-pptx-26-2048.jpg)



![Java
public class Main {
static int count = 2;
public static void fibonacci(int prev1, int prev2) {
if (count <= 19) {
int newFibo = prev1 + prev2;
System.out.println(newFibo);
prev2 = prev1;
prev1 = newFibo;
count += 1;
fibonacci(prev1, prev2);
} else {
return;
}
}
public static void main(String[] args) {
System.out.println(0);
System.out.println(1);
fibonacci(1, 0);
}
}](https://image.slidesharecdn.com/l1-introduction-240616033220-d2d24db9/75/L1-Introduction-for-Computer-Science-pptx-30-2048.jpg)




![Java
public class Main {
public static int F(int n) {
if (n <= 1) {
return n;
} else {
return F(n - 1) + F(n - 2);
}
}
public static void main(String[] args) {
System.out.println(F(19));
}
}](https://image.slidesharecdn.com/l1-introduction-240616033220-d2d24db9/75/L1-Introduction-for-Computer-Science-pptx-35-2048.jpg)