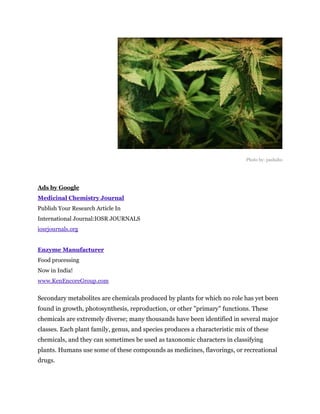
Secondary metabolites are chemicals produced by plants that are not essential for primary functions like growth, photosynthesis or reproduction. They include a wide variety of compounds classified by chemical structure or pathway. Many secondary metabolites help defend plants from herbivores and pathogens. Some have uses as medicines, flavors or recreational drugs and influence plant interactions with other organisms.

1. Law s of therm
Submit
Search
Powered by JRank
Biology Reference
Biology » Re-Se » Secondary Metabolites in Plants - Biology Encyclopedia
Secondary Metabolites in Plants
Ads by Google
Leica Super-Resolution - The Greatest Confocal Resolution With the New Leica TCS SP8
STED. - www.Leica-Microsystems.com/SP8
IGS N2 & O2 Plants - Worldwide supply of Nitrogen and Oxygen Generators - www.igs-
italia.com
Cyclodextrins - 1st time in India DMF available - www.cyclodextrin.com

2. Photo by: pashabo
Ads by Google
Medicinal Chemistry Journal
Publish Your Research Article In
International Journal:IOSR JOURNALS
iosrjournals.org
Enzyme Manufacturer
Food processing
Now in India!
www.KenEncoreGroup.com
Secondary metabolites are chemicals produced by plants for which no role has yet been
found in growth, photosynthesis, reproduction, or other "primary" functions. These
chemicals are extremely diverse; many thousands have been identified in several major
classes. Each plant family, genus, and species produces a characteristic mix of these
chemicals, and they can sometimes be used as taxonomic characters in classifying
plants. Humans use some of these compounds as medicines, flavorings, or recreational
drugs.

3. Secondary metabolites can be classified on the basis of chemical structure (for example,
having rings, containing a sugar), composition (containing nitrogen or not), their
solubility in various solvents, or the pathway by which they are synthesized (e.g.,
phenylpropanoid, which produces tannins). A simple classification includes three main
groups: the terpenes (made from mevalonic acid, composed almost entirely of carbon
and hydrogen), phenolics (made from simple sugars, containing benzene rings,
hydrogen, and oxygen), and nitrogen-containing compounds (extremely diverse, may
also contain sulfur).
The apparent lack of primary function in the plant, combined with the observation that
many secondary metabolites have specific negative impacts on other organisms such as
herbivores and pathogens , leads to the hypothesis that they have evolved because of
their protective value. Many secondary metabolites are toxic or repellant to herbivores
and microbes and help defend plants producing them. Production increases when a
plant is attacked by herbivores or pathogens. Some compounds are released into the air
when plants are attacked by insects; these compounds attract parasites and predators
that kill the herbivores. Recent research is identifying more and more primary roles for
these chemicals in plants as signals, antioxidants , and other functions, so "secondary"
may not be an accurate description in the future.
Consuming some secondary metabolites can have severe consequences. Alkaloids can
block ion channels, inhibit enzymes , or interfere with neurotransmission, producing
hallucinations , loss of coordination, convulsions, vomiting, and death. Some
phenolics interfere with digestion, slow growth, block enzyme activity and cell division,
or just taste awful.
Most herbivores and plant pathogens possess mechanisms that ameliorate the impacts
of plant metabolites, leading to evolutionary associations between particular groups of
pests and plants. Some herbivores (for example, the monarch butterfly) can store
(sequester) plant toxins and gain protection against their enemies. Secondary
metabolites may also inhibit the growth of competitor plants (allelopathy). Pigments
(such as terpenoid carotenes, phenolics, and flavonoids) color flowers and, together with
terpene and phenolic odors, attract pollinators.

4. Secondary chemicals are important in plant use by humans. Most pharmaceuticals are
based on plant chemical structures, and secondary metabolites are widely used for
recreation and stimulation (the alkaloids nicotine and cocaine; the terpene cannabinol).
The study of such plant use is called ethnopharmacology. Psychoactive plant chemicals
are central to some religions, and flavors of secondary compounds shape our food
preferences. The characteristic flavors and aroma of cabbage and relatives are caused by
Class Example Example Some Effects and Uses
Compounds Sources
NITROGEN-
CONTAINING
Alkaloids nicotine cocaine tobacco coca plant interfere with
theobromine chocolate (cocao) neurotransmission, block

5. Class Example Example Some Effects and Uses
Compounds Sources
enzyme action
NITROGEN-AND
SULFUR-
CONTAINING
Glucosinolates sinigrin cabbage, relatives
TERPENOIDS
Monoterpenes menthol linalool mint and relatives, interfere with
many plants neurotransmission, block ion
transport, anesthetic
Sesquiterpenes parthenolid Parthenium and contact dermatitis
relatives (
Asteraceae )
Diterpenes gossypol cotton block phosphorylation; toxic
Triterpenes, cardiac digitogenin Digitalis (foxglove) stimulate heart muscle, alter
glycosides ion transport
Tetraterpenoids carotene many plants antioxidant; orange coloring
Terpene polymers rubber Hevea (rubber) gum up insects; airplane tires
trees, dandelion
Sterols spinasterol spinach interfere with animal hormone
action
PHENOLICS

6. Class Example Example Some Effects and Uses
Compounds Sources
Phenolic acids caffeic, all plants cause oxidative damage,
chlorogenic browning in fruits and wine
Coumarins umbelliferone carrots, parsnip cross-link DNA, block cell
division
Lignans podophyllin mayapple poison cathartic, vomiting, allergic
urushiol ivy dermatitis
Flavonoids anthocyanin, almost all plants flower, leaf color; inhibit
catechin enzymes, anti- and pro-
oxidants, estrogenic
Tannins gallotannin, oak, hemlock trees, bind to proteins, enzymes,
condensed birdsfoot trefoil, block digestion, antioxidants
tannin legumes
Lignin lignin all land plants structure, toughness, fiber
nitrogen-and sulfur-containing chemicals, glucosinolates, which protect these plants
from many enemies. The astringency of wine and chocolate derives from tannins. The
use of spices and other seasonings developed from their combined uses as preservatives
(since they are antibiotic) and flavorings.
SEE ALSO Flowers ; Herbivory and Plant Defenses ; Metabolism, Cellular ; Poisons
Jack Schultz
Bibliography

7. Agosta, William. Bombardier Beetles and Fever Trees: A Close-up Look at Chemical
Warfare and Signals in Animals and Plants. Reading, MA: Addison-Wesley, 1996.
Bidlack, Wayne R. Phytochemicals as Bioactive Agents. Lancaster, PA: Technomic
Publishers, 2000.
Karban, Richard, and Ian T. Baldwin. Induced Responses to Herbivory. Chicago:
University of Chicago Press, 1997.
Rosenthal, Gerald A., and May R. Berenbaum. Herbivores, Their Interactions with
Secondary Plant Metabolites. San Diego, CA: Academic Press, 1991.
Ads by Google
Chemical Crystallography - Inexpensive benchtop XRD system to determine small molecule
structure - www.rigaku.com
User Contributions:
1
aarcee varte
Mar 4, 2008 @ 11:23 pm
please explain how 2 extract secondary metabolites which is not secreted out from plants
and remain inside the plants only
Comment about this article, ask questions, or add new information about this
topic:
Name:

8. E-mail:
Show my email publicly
Type the code shown:
Public Comment: (50-4000 characters)
Send
Secondary Metabolites in Plants - Biology Encyclopedia forum
« Science Writer
Seed Germination and Dormancy »
Copyright © 2013 Advameg, Inc.
Read more: http://www.biologyreference.com/Re-Se/Secondary-Metabolites-in-
Plants.html#ixzz2IdgaAPMf
Cellulose
From Wikipedia, the free encyclopedia

9. Jump to: navigation, search
Cellulose[1]
Identifiers
CAS number 9004-34-6
UNII SMD1X3XO9M
EC-number 232-674-9
ChEMBL CHEMBL1201676
Properties
Molecular formula (C6H10O5)n
Appearance white powder
Density 1.5 g/cm3
Melting point decomp.
Solubility in water none

10. Hazards
EU Index not listed
NFPA 704 1
1
0
Related compounds
Related compounds Starch
(verify) (what is: / ?)
Except where noted otherwise, data are given for materials
in their standard state (at 25 °C, 100 kPa)
Infobox references
Cellulose is an organic compound with the formula (C6H10O5)n, a polysaccharide consisting of a
linear chain of several hundred to over ten thousand β(1→4) linked D-glucose units.[2][3]
Cellulose is the structural component of the primary cell wall of green plants, many forms of
algae and the oomycetes. Some species of bacteria secrete it to form biofilms. Cellulose is the
most common organic compound on Earth. About 33% of all plant matter is cellulose (the
cellulose content of cotton fiber is 90%, that of wood is 40–50% and that of dried hemp is
approximately 75%).[4][5][6]
For industrial use, cellulose today is mainly obtained from wood pulp and cotton. Cellulose is
mainly used to produce paperboard and paper; to a smaller extent it is converted into a wide
variety of derivative products such as cellophane and rayon. Converting cellulose from energy
crops into biofuels such as cellulosic ethanol is under investigation as an alternative fuel source.
Some animals, particularly ruminants and termites, can digest cellulose with the help of
symbiotic micro-organisms that live in their guts. Humans can digest cellulose to some

11. extent,[7][8] however it mainly acts as a hydrophilic bulking agent for feces and is often referred
to as "dietary fiber".
Contents
1 History
2 Products
o 2.1 Cellulose source and energy crops
3 Structure and properties
4 Assaying a cellulose-containing material
5 Biosynthesis
6 Breakdown (cellulolysis)
7 Hemicellulose
8 Derivatives
9 References
10 External links
[edit] History
Cellulose was discovered in 1838 by the French chemist Anselme Payen, who isolated it from
plant matter and determined its chemical formula.[2][9][10] Cellulose was used to produce the first
successful thermoplastic polymer, celluloid, by Hyatt Manufacturing Company in 1870.
Hermann Staudinger determined the polymer structure of cellulose in 1920. The compound was
first chemically synthesized (without the use of any biologically derived enzymes) in 1992, by
Kobayashi and Shoda.[11]
Cellulose in a plant cell.
[edit] Products

12. Cotton fibres represent the purest natural form of cellulose, containing more than 90% of this
carbohydrate.
See also: dissolving pulp and pulp (paper)
The kraft process is used to separate cellulose from lignin, another major component of plant
matter. Cellulose is the major constituent of paper, paperboard, and card stock and of textiles
made from cotton, linen, and other plant fibers.
Cellulose can be converted into cellophane, a thin transparent film, and into rayon, an important
fiber that has been used for textiles since the beginning of the 20th century. Both cellophane and
rayon are known as "regenerated cellulose fibers"; they are identical to cellulose in chemical
structure and are usually made from dissolving pulp via viscose. A more recent and
environmentally friendly method to produce a form of rayon is the Lyocell process. Cellulose is
the raw material in the manufacture of nitrocellulose (cellulose nitrate) which is used in
smokeless gunpowder and as the base material for celluloid used for photographic and movie
films until the mid 1930s.
Cellulose is used to make water-soluble adhesives and binders such as methyl cellulose and
carboxymethyl cellulose which are used in wallpaper paste. Microcrystalline cellulose (E460i)
and powdered cellulose (E460ii) are used as inactive fillers in tablets[12] and as thickeners and
stabilizers in processed foods. Cellulose powder is for example used in Kraft's Parmesan cheese
to prevent caking inside the tube.
Cellulose is used in the laboratory as the stationary phase for thin layer chromatography.
Cellulose fibers are also used in liquid filtration, sometimes in combination with diatomaceous
earth or other filtration media, to create a filter bed of inert material. Cellulose is further used to
make hydrophilic and highly absorbent sponges.
Cellulose insulation made from recycled paper is becoming popular as an environmentally
preferable material for building insulation. It can be treated with boric acid as a fire retardant.
Cellulose consists of crystalline and amorphous regions. By treating it with strong acid, the
amorphous regions can be broken up, thereby producing nanocrystalline cellulose, a novel
material with many desirable properties.[13] Recently, nanocrystalline cellulose was used as the

13. filler phase in bio-based polymer matrices to produce nanocomposites with superior thermal and
mechanical properties. [14]
[edit] Cellulose source and energy crops
Main article: Energy crop
The major combustible component of non-food energy crops is cellulose, with lignin second.
Non-food energy crops are more efficient than edible energy crops (which have a large starch
component), but still compete with food crops for agricultural land and water resources.[15]
Typical non-food energy crops include industrial hemp (though outlawed in some countries),
switchgrass, Miscanthus, Salix (willow), and Populus (poplar) species.
Some bacteria can convert cellulose into ethanol which can then be used as a fuel; see cellulosic
ethanol.
A strand of cellulose (conformation Iα), showing the hydrogen bonds (dashed) within and between
cellulose molecules.
[edit] Structure and properties
Cellulose has no taste, is odorless, is hydrophilic with the contact angle of 20–30,[16] is insoluble
in water and most organic solvents, is chiral and is biodegradable. It can be broken down
chemically into its glucose units by treating it with concentrated acids at high temperature.
Cellulose is derived from D-glucose units, which condense through β(1→4)-glycosidic bonds.
This linkage motif contrasts with that for α(1→4)-glycosidic bonds present in starch, glycogen,
and other carbohydrates. Cellulose is a straight chain polymer: unlike starch, no coiling or
branching occurs, and the molecule adopts an extended and rather stiff rod-like conformation,
aided by the equatorial conformation of the glucose residues. The multiple hydroxyl groups on
the glucose from one chain form hydrogen bonds with oxygen atoms on the same or on a
neighbor chain, holding the chains firmly together side-by-side and forming microfibrils with

14. high tensile strength. This strength is important in cell walls, where the microfibrils are meshed
into a carbohydrate matrix, conferring rigidity to plant cells.
A triple strand of cellulose showing the hydrogen bonds (cyan lines) between glucose strands
Compared to starch, cellulose is also much more crystalline. Whereas starch undergoes a
crystalline to amorphous transition when heated beyond 60–70 °C in water (as in cooking),
cellulose requires a temperature of 320 °C and pressure of 25 MPa to become amorphous in
water.[17]
Several different crystalline structures of cellulose are known, corresponding to the location of
hydrogen bonds between and within strands. Natural cellulose is cellulose I, with structures Iα
and Iβ. Cellulose produced by bacteria and algae is enriched in Iα while cellulose of higher plants
consists mainly of Iβ. Cellulose in regenerated cellulose fibers is cellulose II. The conversion of
cellulose I to cellulose II is irreversible, suggesting that cellulose I is metastable and cellulose II
is stable. With various chemical treatments it is possible to produce the structures cellulose III
and cellulose IV.[18]
Many properties of cellulose depend on its chain length or degree of polymerization, the number
of glucose units that make up one polymer molecule. Cellulose from wood pulp has typical chain
lengths between 300 and 1700 units; cotton and other plant fibers as well as bacterial cellulose
have chain lengths ranging from 800 to 10,000 units.[11] Molecules with very small chain length
resulting from the breakdown of cellulose are known as cellodextrins; in contrast to long-chain
cellulose, cellodextrins are typically soluble in water and organic solvents.
Plant-derived cellulose is usually found in a mixture with hemicellulose, lignin, pectin and other
substances, while microbial cellulose is quite pure, has a much higher water content, and consists
of long chains.
Cellulose is soluble in cupriethylenediamine (CED), cadmiumethylenediamine (Cadoxen), N-
methylmorpholine N-oxide and lithium chloride / dimethylformamide.[19] This is used in the
production of regenerated celluloses (such as viscose and cellophane) from dissolving pulp.
[edit] Assaying a cellulose-containing material
Given a cellulose-containing material, the carbohydrate portion that does not dissolve in a 17.5%
solution of sodium hydroxide at 20 °C is α cellulose, which is true cellulose. Acidification of the
extract precipitates β cellulose. The portion that dissolves in base but does not precipitate with
acid is γ cellulose.

15. Cellulose can be assayed using a method described by Updegraff in 1969, where the fiber is
dissolved in acetic and nitric acid to remove lignin, hemicellulose, and xylosans. The resulting
cellulose is allowed to react with anthrone in sulfuric acid. The resulting coloured compound is
assayed spectrophotometrically at a wavelength of approximately 635 nm.
In addition, cellulose is represented by the difference between acid detergent fiber (ADF) and
acid detergent lignin (ADL).
[edit] Biosynthesis
Location and arrangement of cellulose microfibrils in the plant cell wall
In vascular plants cellulose is synthesized at the plasma membrane by rosette terminal complexes
(RTCs). The RTCs are hexameric protein structures, approximately 25 nm in diameter, that
contain the cellulose synthase enzymes that synthesise the individual cellulose chains.[20] Each
RTC floats in the cell's plasma membrane and "spins" a microfibril into the cell wall.
RTCs contain at least three different cellulose synthases, encoded by CesA genes, in an unknown
stoichiometry.[21] Separate sets of CesA genes are involved in primary and secondary cell wall
biosynthesis.
Cellulose synthesis requires chain initiation and elongation, and the two processes are separate.
CesA glucosyltransferase initiates cellulose polymerization using a steroid primer, sitosterol-
beta-glucoside, and UDP-glucose.[22] Cellulose synthase utilizes UDP-D-glucose precursors to
elongate the growing cellulose chain. A cellulase may function to cleave the primer from the
mature chain.
Cellulose is also synthesised by animals, particularly in the tests of ascidians (where the cellulose
was historically termed "tunicine") although it is also a minor component of mammalian
connective tissue.[23]
[edit] Breakdown (cellulolysis)
Cellulolysis is the process of breaking down cellulose into smaller polysaccharides called
cellodextrins or completely into glucose units; this is a hydrolysis reaction. Because cellulose
molecules bind strongly to each other, cellulolysis is relatively difficult compared to the
breakdown of other polysaccharides.[24] Processes do exist however for the breakdown of

16. cellulose such as the Lyocell process [25] which uses a combination of heated water and acetone
to break down the cellulose strands.
Most mammals have only very limited ability to digest dietary fibres such as cellulose. Some
ruminants like cows and sheep contain certain symbiotic anaerobic bacteria (like Cellulomonas)
in the flora of the rumen, and these bacteria produce enzymes called cellulases that help the
microorganism to break down cellulose; the breakdown products are then used by the bacteria
for proliferation. The bacterial mass is later digested by the ruminant in its digestive system
(stomach and small intestine). Similarly, lower termites contain in their hindguts certain
flagellate protozoa which produce such enzymes; higher termites contain bacteria for the job.
Some termites may also produce cellulase of their own.[26] Fungi, which in nature are responsible
for recycling of nutrients, are also able to break down cellulose.
The enzymes utilized to cleave the glycosidic linkage in cellulose are glycoside hydrolases
including endo-acting cellulases and exo-acting glucosidases. Such enzymes are usually secreted
as part of multienzyme complexes that may include dockerins and carbohydrate-binding
modules.[27]
[edit] Hemicellulose
Main article: Hemicellulose
Hemicellulose is a polysaccharide related to cellulose that comprises about 20% of the biomass
of most plants. In contrast to cellulose, hemicellulose is derived from several sugars in addition
to glucose, especially xylose but also including mannose, galactose, rhamnose, and arabinose.
Hemicellulose consists of shorter chains – around 200 sugar units. Furthermore, hemicellulose is
branched, whereas cellulose is unbranched.
[edit] Derivatives
The hydroxyl groups (-OH) of cellulose can be partially or fully reacted with various reagents to
afford derivatives with useful properties like mainly cellulose esters and cellulose ethers (-OR).
In principle, though not always in current industrial practice, cellulosic polymers are renewable
resources.
Ester derivatives include:
Cellulose
Reagent Example Reagent Group R
ester
Organic Organic Acetic acid and acetic
Cellulose acetate H or -(C=O)CH3
esters acids anhydride
Acetic acid and acetic
Cellulose triacetate -(C=O)CH3
anhydride

17. Cellulose propionate Propanoic acid H or -(C=O)CH2CH3
Cellulose acetate Acetic acid and propanoic H or -(C=O)CH3 or -
propionate acid (C=O)CH2CH3
Cellulose acetate H or -(C=O)CH3 or -
Acetic acid and butyric acid
butyrate (C=O)CH2CH2CH3
Inorganic Inorganic Nitrocellulose Nitric acid or another
H or -NO2
esters acids (cellulose nitrate) powerful nitrating agent
Sulfuric acid or another
Cellulose sulfate H or -SO3H
powerful sulfuring agent
The cellulose acetate and cellulose triacetate are film- and fiber-forming materials that find a
variety of uses. The nitrocellulose was initially used as an explosive and was an early film
forming material. With camphor, nitrocellulose gives celluloid.
Ether derivatives include:
Water E
Cellulose Group R = H
Reagent Example Reagent solubilit Application numbe
ethers or
y r
Cold
Halogenoalkan Methylcellulo Chloromethan
Alkyl -CH3 water E461
es se e
soluble
A
commercial
thermoplasti
c used in
Water
coatings,
Ethylcellulose Chloroethane -CH2CH3 insolubl E462
inks, binders,
e
and
controlled-
release drug
tablets
Ethyl methyl Chloromethan -CH3 or - E465
cellulose e and CH2CH3

18. chloroethane
Cold/ho Gelling and
Hydroxyalk Hydroxyethyl Ethylene
Epoxides -CH2CH2OH t water thickening
yl cellulose oxide
soluble agent
Hydroxypropy - Cold
Propylene
l cellulose CH2CH(OH)C water E463
oxide
(HPC) H3 soluble
Chloromethan
Hydroxyethyl Cold Production of
e and -CH3 or -
methyl water cellulose
ethylene CH2CH2OH
cellulose soluble films
oxide
Viscosity
Hydroxypropy Chloromethan modifier,
-CH3 or - Cold
l methyl e and gelling,
CH2CH(OH)C water E464
cellulose propylene foaming and
H3 soluble
(HPMC) oxide binding
agent
Ethyl Chloroethane
-CH2CH3 or—
hydroxyethyl and ethylene E467
CH2CH2OH
cellulose oxide
Often used
as its sodium
Carboxymethy Cold/Ho
Carboxyalk Halogenated Chloroacetic salt, sodium
l cellulose -CH2COOH t water E466
yl carboxylic acids acid carboxymeth
(CMC) soluble
yl cellulose
(NaCMC)
The sodium carboxymethyl cellulose can be cross-linked to give the croscarmellose sodium
(E468) for use as a disintegrant in pharmaceutical formulations.
[edit] References
1. ^ Nishiyama, Yoshiharu; Langan, Paul; Chanzy, Henri (2002). "Crystal Structure and Hydrogen-Bonding
System in Cellulose Iβ from Synchrotron X-ray and Neutron Fiber Diffraction". J. Am. Chem. Soc 124 (31):
9074–82. doi:10.1021/ja0257319. PMID 12149011..
ab
2. ^ Crawford, R. L. (1981). Lignin biodegradation and transformation. New York: John Wiley and Sons.
ISBN 0-471-05743-6.

19. 3. ^ Updegraff DM (1969). "Semimicro determination of cellulose in biological materials". Analytical
Biochemistry 32 (3): 420–424. doi:10.1016/S0003-2697(69)80009-6. PMID 5361396.
4. ^ Cellulose. (2008). In Encyclopædia Britannica. Retrieved January 11, 2008, from Encyclopædia Britannica
Online.
5. ^ Chemical Composition of Wood
6. ^ G. Buschle-Diller, C. Fanter, F. Loth (April 1999). "Structural changes in hemp fibers as a result of
enzymatic hydrolysis with mixed enzyme systems". Textile Research Journal 69 (4): 244-251.
http://www.globalhemp.com/1999/04/structural-changes-in-hemp-fibers-as-a-result-of-enzymatic-
hydrolysis-with-mixed-enzyme-systems.html.
7. ^ Slavin, JL; Brauer, PM; Marlett, JA (1981). "Neutral detergent fiber, hemicellulose and cellulose
digestibility in human subjects.". The Journal of Nutrition 111 (2): 287–97. PMID 6257867.
8. ^ Joshi, S; Agte, V (1995). "Digestibility of dietary fiber components in vegetarian men.". Plant foods for
human nutrition (Dordrecht, Netherlands) 48 (1): 39–44. doi:10.1007/BF01089198. PMID 8719737.
9. ^ A. Payen (1838) "Mémoire sur la composition du tissu propre des plantes et du ligneux" (Memoir on the
composition of the tissue of plants and of woody [material]), Comptes rendus, vol. 7, pages 1052-1056.
Payen added appendices to this paper on December 24, 1838 (see: Comptes rendus, vol. 8, page 169
(1839)) and on February 4, 1839 (see: Comptes rendus, vol. 9, page 149 (1839)). A committee of the
French Academy of Sciences reviewed Payen's findings in : Jean-Baptiste Dumas (1839) "Rapport sur un
mémoire de M. Payen, relatif à la composition de la matière ligneuse" (Report on a memoir of Mr. Payen,
regarding the composition of woody matter), Comptes rendus, vol. 8, pages 51-53. In this report, the word
"cellulose" is coined and author points out the similarity between the empirical formula of cellulose and
that of "dextrine" (starch). The above articles are reprinted in: Brongniart and Guillemin, eds., Annales des
sciences naturelles ..., 2nd series, vol. 11 (Paris, France: Crochard et Cie., 1839), pages 21-31.
10. ^ Young, Raymond (1986). Cellulose structure modification and hydrolysis. New York: Wiley. ISBN 0-471-
82761-4.
ab
11. ^ Klemm, Dieter; Brigitte Heublein, Hans-Peter Fink, Andreas Bohn (2005). "Cellulose: Fascinating
Biopolymer and Sustainable Raw Material". ChemInform 36 (36). doi:10.1002/chin.200536238.
12. ^ Weiner, Myra L.; Lois A. Kotkoskie (2000). Excipient Toxicity and Safety. New York ; Dekker. p. 210.
ISBN 0-8247-8210-0.
13. ^ Peng, B. L., Dhar, N., Liu, H. L. and Tam, K. C. (2011). "Chemistry and applications of nanocrystalline
cellulose and its derivatives: A nanotechnology perspective.". The Canadian Journal of Chemical
Engineering 89 (5): 1191–1206.
http://www.arboranano.ca/pdfs/Chemistry%20and%20applications%20of%20nanocrystalline%20cellulos
e%20and%20its%20derivatives%20A%20nanotechnology%20perspective-2011.pdf.
14. ^ Lawrence Pranger and Rina Tannenbaum "Biobased nanocomposites prepared by in situ polymerization
of furfuryl alcohol with cellulose whiskers or montmorillonite clay" Macromolecules 41 (2008) 8682.
http://dx.doi.org/10.1021/ma8020213
15. ^ Holt-Gimenez, Eric 2007. Biofuels: Myths of the Agrofuels Transition. Backgrounder. Institute for Food
and Development Policy, Oakland, CA. 13:2
16. ^ Charles A. Bishop, ed. (2007). Vacuum deposition onto webs, films, and foils, Volume 0, Issue 8155.
p. 165. ISBN 0-8155-1535-9. http://books.google.com/books?id=vP9E3z7o6iIC&pg=PA165.
17. ^ Deguchi, Shigeru; Tsujii, Kaoru; Horikoshi, Koki (2006). "Cooking cellulose in hot and compressed water".
Chemical Communications (31): 3293. doi:10.1039/b605812d.
18. ^ Structure and morphology of cellulose by Serge Pérez and William Mackie, CERMAV-CNRS, 2001.
Chapter IV.
19. ^ Stenius, Per (2000). "1". Forest Products Chemistry. Papermaking Science and Technology. 3. Finland:
Fapet OY. p. 35. ISBN 952-5216-03-9.
20. ^ Kimura, S; Laosinchai, W; Itoh, T; Cui, X; Linder, CR; Brown Jr, RM (1999). "Immunogold labeling of
rosette terminal cellulose-synthesizing complexes in the vascular plant vigna angularis". The Plant cell 11
(11): 2075–86. doi:10.2307/3871010. JSTOR 3871010. PMC 144118. PMID 10559435.
//www.ncbi.nlm.nih.gov/pmc/articles/PMC144118/.
21. ^ Taylor, N. G. (2003). "Interactions among three distinct CesA proteins essential for cellulose synthesis".
Proceedings of the National Academy of Sciences 100 (3): 1450. doi:10.1073/pnas.0337628100.

20. 22. ^ Peng, L; Kawagoe, Y; Hogan, P; Delmer, D (2002). "Sitosterol-beta-glucoside as primer for cellulose
synthesis in plants". Science 295 (5552): 147–50. doi:10.1126/science.1064281. PMID 11778054.
23. ^ Endean, The Test of the Ascidian, Phallusia mammillata, Quarterly Journal of Microscopical Science, Vol.
102, part 1, pp. 107-117, 1961.
24. ^ David G. Barkalow, Roy L. Whistler, "Cellulose", in AccessScience, McGraw-Hill, doi:10.1036/1097-
8542.118200. Retrieved 11 January 2008.
25. ^ H.Lyocell, "Cellulose" Issue 41, pp 419
26. ^ Tokuda, G; Watanabe, H (22 June 2007). "Hidden cellulases in termites: revision of an old hypothesis".
Biology Letters 3 (3): 336–339. doi:10.1098/rsbl.2007.0073. PMC 2464699. PMID 17374589.
http://rsbl.royalsocietypublishing.org/content/3/3/336.long
27. ^ Brás, Natércia; N. M. F. S. A. Cerqueira, P. A. Fernandes, M. J. Ramos (2008). "Carbohydrate Binding
Modules from family 11: Understanding the binding mode of polysaccharides". International Journal of
Quantum Chemistry 108 (11): 2030–2040. doi:10.1002/qua.21755.
[edit] External links
Structure and morphology of cellulose by Serge Pérez and William Mackie, CERMAV-CNRS
Cellulose, by Martin Chaplin, London South Bank University
Clear description of a cellulose assay method at the Cotton Fiber Biosciences unit of the USDA.
Cellulose films could provide flapping wings and cheap artificial muscles for robots -
TechnologyReview.com
Using cellulase enzymes in the bioethanol process
A list of cellulolytic bacteria
v
t
e
Types of carbohydrates
Aldose
Furanose
General
Ketose
Pyranose
Anomer
Geometry Cyclohexane conformation
Mutarotation

21. Aldodiose
Dioses
o Glycolaldehyde
Aldotriose
o Glyceraldehyde
Trioses
Ketotriose
o Dihydroxyacetone
Aldotetroses
o Erythrose
Tetroses o Threose
Ketotetrose
o Erythrulose
Monosaccharides
Aldopentose
o Arabinose
o Lyxose
o Ribose
o Xylose
Pentoses
Deoxy sugar
o Deoxyribose
Ketopentose
o Ribulose
o Xylulose
Aldohexose
Hexoses
o Allose
o Altrose

22. o Galactose
o Glucose
o Gulose
o Idose
o Mannose
o Talose
Deoxy sugar
o Fucose
o Fuculose
o Rhamnose
Ketohexose
o Fructose
o Psicose
o Sorbose
o Tagatose
Ketoheptose
Heptoses o Mannoheptulose
o Sedoheptulose
Octose
>7 Nonose
o Neuraminic acid
Cellobiose
Multiple Disaccharides Lactose
Maltose
Sucrose

23. Trehalose
Turanose
Maltotriose
Trisaccharides Melezitose
Raffinose
Tetrasaccharides Stachyose
Acarbose
Fructooligosaccharide (FOS)
Other Galactooligosaccharide (GOS)
oligosaccharides Isomaltooligosaccharide (IMO)
Maltodextrin
Mannan-oligosaccharides (MOS)
Beta-glucan
o Lentinan
o Sizofiran
o Zymosan
Cellulose
Polysaccharides Chitin
Dextrin / Dextran
Fructose / Fructan
o Inulin
Galactose / Galactan
Glucose / Glucan
o Glycogen

24. Levan beta 2→6
Mannan
Starch
o Amylopectin
o Amylose
biochemical families: carbohydrates
o alcohols
o glycoproteins
o glycosides
lipids
o eicosanoids
o fatty acids / intermediates
o phospholipids
o sphingolipids
o steroids
nucleic acids
o constituents / intermediates
proteins
o amino acids / intermediates
tetrapyrroles / intermediates
v
t
e
Paper
History
Wood pulp
Materials
Fiber crop
Papyrus

25. Paper chemicals
Blotting
Bond
Construction
Copy
Cotton
Crêpe
Glassine
India
Kraft
Laid
Manila
Newsprint
Types Onionskin
Origami
Rag
Rice
Security
Seed
Tar
Tissue
Tracing
Transfer
Wallpaper
Waterproof
Wax
Wood-free

26. Wove
Size
Specifications
Density
Papermaking
Paper engineering
Paper mill
Paper machine
Production
Sulfite process
Kraft process
Soda pulping
Paper recycling
List of paper mills
In Europe
Industry
In the United States
In Japan
Bleaching of wood pulp
Issues Environmental impact of paper
Paper pollution
Category Commons
Retrieved from "http://en.wikipedia.org/w/index.php?title=Cellulose&oldid=531575776"
Categories:
Cellulose
Excipients
Papermaking
Polysaccharides

27. Hidden categories:
Chemical compounds which do not have a ChemSpiderID
Chemboxes which contain changes to verified fields
Navigation menu
Personal tools
Create account
Log in
Namespaces
Article
Talk
Variants
Views
Read
Edit
View history
Actions
Search
Navigation
Main page
Contents
Featured content
Current events
Random article
Donate to Wikipedia
Interaction
Help
About Wikipedia
Community portal
Recent changes

28. Contact Wikipedia
Toolbox
What links here
Related changes
Upload file
Special pages
Permanent link
Page information
Cite this page
Print/export
Create a book
Download as PDF
Printable version
Languages
‫ال عرب ية‬
Azərbaycanca
Беларуская
Б
Български
Bosanski
Català
Česky
Dansk
Deutsch
Eesti
Ελληνικά
Español
Esperanto
Euskara
‫ف ار سی‬
Français
Galego
한국어
Hrvatski
Ido
Bahasa Indonesia
Íslenska
Italiano
‫עברית‬
ქართული
Қазақша

29. Kreyòl ayisyen
Latviešu
Lietuvių
Magyar
Македонски
მარგალური
Bahasa Melayu
Nederlands
日本語
Occitan
Polski
Português
Română
Runa Simi
Русский
Shqip
Simple English
Slovenčina
Slovenščina
Српски / srpski
Srpskohrvatski / српскохрватски
Basa Sunda
Suomi
Svenska
Türkçe
Українська
Tiếng Việt
中文
This page was last modified on 6 January 2013 at 05:57.
Text is available under the Creative Commons Attribution-ShareAlike License; additional terms
may apply. See Terms of Use for details.
Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit
organization.
Contact us
Privacy policy
About Wikipedia
Disclaimers
Mobile view

30. Introduction
Some useful constants in thermodynamics:
1 eV = 9.6522E4 J/mol
k Boltzmann's constant = 1.38E-23 J/K
volume: 1 cm3 = 0.1 kJ/kbar = 0.1 J/bar
mole: 1 mole of a substance contains Avogadro's number (N = 6.02E23) of molecules.
Abbreviated as 'mol'.
atomic weights are based around the definition that 12C is exactly 12 g/mol
R gas constant = Nk = 8.314 J mol-1 K-1
Units of Temperature: Degrees Celsius and Kelvin
The Celsius scale is based on defining 0 °C as the freezing point of water and 100°C as the boiling point.
The Kelvin scale is based on defining 0 K, "absolute zero," as the temperature at zero pressure
where the volumes of all gases is zero--this turns out to be -273.15 °C. This definition means that
the freezing temperature of water is 273.15 K. All thermodynamic calculations are done in
Kelvin!
kilo and kelvin: write k for 1000's and K for kelvin. Never write °K.
Units of Energy: Joules and Calories
Joules and calories and kilocalories: A calorie is defined as the amount of energy required to raise the
temperature of 1 g of water from 14.5 to 15.5°C at 1 atm.
4.184 J = 1 cal; all food 'calories' are really kcal.

31. Many times it is easiest to solve equations or problems by conducting "dimensional analysis,"
which just means using the same units throughout an equation, seeing that both sides of an
equation contain balanced units, and that the answer is cast in terms of units that you want. As an
example, consider the difference between temperature (units of K) and heat (units of J). Two
bodies may have the same temperature, but contain different amounts of heat; likewise, two
bodies may contain the same heat, but be at different temperatures. The quantity that links these
two variables must have units of J/K or K/J. In fact, the heat capacity C describes the amount of
heat dQ involved in changing one mole of a substance by a given temperature increment dT:
dQ = CdT
The heat capacity C is then
C = dQ/dT
and must have units of J K-1 mol-1. (The specific heat is essentially the same number, but is expressed per
gram rather than per mole.)
Don't forget significant digits. 1*2=2; 1.1*2=2; 1.1*2.0=2.2; 1.0*2.0=2.0
Why Thermodynamics?
Think about some everyday experiences you have with chemical reactions.
Your ability to melt and refreeze ice shows you that H2O has two phases and that the reaction
transforming one to the other is reversible--apparently the crystallization of ice requires removing some
heat.
Frying an egg is an example of an irreversible reaction.
If you dissolve halite in water you can tell that the NaCl is still present in some form by tasting the water.
Why does the NaCl dissolve? Does it give off heat? Does it require energy?
How is it that diamond, a high-pressure form of C, can coexist with the low pressure form, graphite, at
Earth's surface? Do diamond and graphite both have the same energy? If you burn graphite and
diamond, which gives you more energy?
When dynamite explodes, why does it change into a rapidly expanding gas, which provides the energy
release, plus a few solids?
Chemical thermodynamics provides us with a means of answering these questions and more.
A Few Definitions
A system is any part of the universe we choose to consider.
Matter and energy can flow in or out of an open system but only energy can be added to or subtracted
from a closed system. An isolated system is one in which matter and energy are conserved.
A phase is a homogeneous body of matter. The components of a system are defined by a set of
chemical formula used to describe the system.
The phase rule:

32. F + P = C + 2.
Extensive parameters are proportional to mass (e.g., V, mass, energy).
Intensive parameters are independent of mass (e.g., P, T); these are the "degrees of freedom" F
contained in the phase rule.
Thermodynamics: Power and Limitations
Thermodynamics allows you to predict how chemical systems should behave from a supra-atomic
"black-box" level--it says nothing about how chemical systems will behave. Thermodynamics also
pertains to the state of a system, and says nothing about the path taken by the system in changing from
one state to another.
Chemical Reactions and Equations
How to write chemical reactions; stoichiometry.
Mass and charge balance: e.g.,
2Fe3+ + 3H2O = Fe2O3 + 6H+
Reaction-Produced Change in Mass, Density, Volume
The change in volume rV of a reaction is the volume V of the products minus the volume of the
reactants:
rV = Vproducts - Vreactants
Thus, if the products are smaller than the reactants, rV < 0.
In a generalized reaction such as
aA + bB ... = cC + dD...
rV = cVC + dVD - aVA - bVB
This sort of additive relationship is true for other state variables and is usually stated as
r i i
where i are the stoichiometric coefficients, positive for products and negative for reactants.
What Actually Drives Reactions? Is it Energy? Can We Just Calculate or Measure the Energy
Difference of Reactants and Products and Know Which Way the Reaction Will Go?

33. For many years people felt that chemical reactions occurred because the reactants had some kind of
energy to give up (i.e., use to do work)--and that therefore the energy of the products would be less
than the energy of the reactants. However, we all know that when ice melts it consumes rather than
releases heat, so there must be more to the story behind why chemical reactions occur.
Le Chatelier's Principle
"If a change is made to a system, the system will respond so as to absorb the force causing the change."
Equilibrium
A mechanical analogy for chemical change is that of a ball rolling down a slope with multiple valleys; we
explain the ball's behavior by saying that mechanical systems have a tendency to reduce their potential
energy.
At equilibrium none of the properties of a system change with time. A system at equilibrium returns to
equilibrium if disturbed.
"Stable" describes a system or phase in its lowest energy state.
"Metastable" describes a system or phase in any other energy state.
The figure above shows the mechanical analogy for H2O at -5°C and + 5°C and 1 atm. Left: at -5°C, solid
H2O has the lowest possible energy state. Right: at +5°C, liquid H2O has the lowest possible energy state.
When solid H2O is actually present at +5°C, the difference between the free energy of solid H2O and
liquid H2O is available to drive the reaction to form the stable solid H2O phase, and the reaction will go
to completion if kinetically possible.

34. Energy: How Do We Calculate and Measure Energy and How Can We Use this Knowledge to
Predict Reaction Behavior?
Thermodynamics works equally well to describe any kind of work or energy: magnetic, potential, kinetic,
etc. For geological systems we typically talk about pressure-volume work, which, because mechanical
work is F x, you can imagine might be
P V
or
V P
Because we noted that rV < 0 if the products are smaller than the reactants, we choose to write the P-
V work term as
-P V
so that a decrease in volume - V is seen as positive work or that an increase in volume + V results in
a decrease in crystal energy.
The absolute energy of a body can be calculated from Einstein's equation U=mc2, but the presence of
the c2 term means that the energy of any system is quite large and that measuring this energy is
impractical. It is more practical to measure differences in energy U, and we always discuss or measure
differences relative to some arbitrary standard state. Analogous to this might be if someone in Namibia
asked you to measure the elevation of the crests of waves at Campus Point--without agreement on
some kind of standard, you wouldn't be able to do much more than measure the heights of individual
waves. If however, you could both agree on an equivalent "sea level" at both localities, you could then
compare the absolute elevations of the wave crests.
A typical thermodynamic standard state is normal laboratory conditions: 25°C (298.15 K) and 1
atm (often called STP for standard temperature and pressure).
The internal energy U of a mineral is the sum of the potential energy stored in the interatomic
bonds and the kinetic energy of the atomic vibrations. Thus, you might expect that weakly
bonded minerals have relatively low potential energy and thus low internal energy, and when a
mineral is cold such that its atomic vibrations are slow it will have low kinetic energy and thus
low internal energy. Internal energies are always defined relative to some non-zero standard
state, so we typically talk about changes in internal energy dU.
An Aside on Differences and Differentials
What's the difference among , d , and ?
is used to indicate any kind of difference.

35. d is used to indicate a differential.
is used to indicate a partial differential. For example, the partial differential, with respect to y, of
f(x,y) = x3y4
is
= 4x3y3
First Law of Thermodynamics
Adding heat Q to a crystal increases its internal energy U:
dU dQ
( indicates 'proportional') but if the crystal is allowed to expand, some of the added energy will be
consumed by expansion dV, so the total energy of the crystal is reduced:
dU = dQ - PdV
This is effectively the First Law of Thermo: that total energy (heat + P-V work) is conserved.
Heat Capacity
Heat capacity C describes the amount of heat required to change the temperature of a substance:
C=
By definition, the heat capacity of water at 15°C is 1 cal K-1 g-1 or 18 cal K-1 mol-1 (i.e., the heat required
to heat 1 gram of water from 14.5 to 15.5°C is 1 calorie).
Heat capacities of solids approach zero as absolute zero is approached:
C=0
The heat capacity is written with a subscript P or V depending on whether it obtains for constant
pressure CP or constant volume CV.
As an aside,
2
CP = CV + TV /

36. where and are the expansivity and compressibility--for solids the difference between CP and CV is
minimal and can be ignored as a first approximation. For gases, CP = CV + R, and is quite significant.
Heat capacities are measured by calorimetry and often fit by a function of the form:
CP = a + bT + cT-2 + dT-0.5
but there are other expansions for the heat capacity involving more or fewer terms.
Below are some examples of heat capacities of minerals. Note how silicates have a nearly constant heat
capacity of ~1 J K-1 g-1 above 400K.

37. Enthalpy
We have already talked about the familiar concept of heat as energy.
Let's define another measure of energy called enthalpy H--a kind of measure of the thermal energy of a
crystal. As we will see below,

38. dH = dQ + VdP
Recall that we interpreted
dU = dQ - PdV
to mean that the internal energy change is the heat change minus the energy lost to relaxation of the
crystal. Thus,
dH = dQ + VdP
means that the enthalpy change is the heat change plus the energy the crystal gains by virtue of not
being allowed to expand.
Enthalpy includes the vibrational and bonding energy at absolute zero H0°, plus the energy required to
increase temperature:
H = H0° + CPdT
i.e., we can find the enthalpy change H produced by changing temperature by integrating the heat
capacity CP:
H= CPdT
Integration Reminder
How to integrate the heat capacity (to determine change in enthalpy H):
CP dT = (a + bT + cT-2 + dT-0.5)
=aT + bT2/2 - c/T + 2dT0.5
and is evaluated as
=a(T2 - T1) + b(T22 - T12)/2 - c/(T2-1 - T1-1) + 2d(T20.5 - T10.5)
How to integrate the heat capacity divided by T (to determine entropy S):
dT = (a/T + b + cT-3 + dT-1.5)

39. = a ln T + b T - c T-2/2 - 2 d T -0.5
and is evaluated as
a(ln T2 - ln T1) + b(T2 - T1) - c(T2-2 - T1-2)/2 - 2d(T2-0.5 - T1-0.5)
As an example, let's calculate the change in enthalpy H°298-1000 that results from heating quartz
from 298 K to 1000 K, given the following heat capacity expansion coefficients:
a = 104.35, b = 6.07E-3, c = 3.4E+4, d = -1070
(CP dT = (a + bT + cT-2 + dT-0.5)
=aT + bT2/2 - c/T + 2dT0.5
evaluated from 298 to 1000K
=a*(1000-298) + b*(10002-2982)/2 - c*(1000-1-298-1) + 2d*(10000.5-2980.5)
= 45.37 kJ/mol
Relation Among Enthalpy, Heat, and Heat Capacity ( HP= QP)
An important relationship between enthalpy change H and heat change Q is revealed by
differentiating H = U + PV to obtain the total differential
dH = dU + PdV + VdP
substituting dU = dQ - PdV we get
dH = dQ + VdP
dividing by dT gives
= -V
at constant pressure, = 0, leaving
=

40. which is equal to CP:
= = CP
Determining Enthalpies
Thus, if we want to measure how the internal energy U of a crystal changes U with increasing
temperature at constant pressure, we want to know H, and we can get that by integrating the heat
capacity CP over the temperature range of interest.
There's another way to measure H, though: calorimetry. By dissolving a mineral in acid and measuring
the heat produced by the dissolution, we get a heat of dissolution (usually positive). The enthalpy of
"formation" fH° of the mineral is then just the opposite of the heat of dissolution (usually negative).
Exceptions to the "usually positive/negative" rule include CN, HCN, Cu2+, Hg2+, NO, Ag+, and S2-.
Enthalpies of formation appear in tables of thermodynamic data and are usually referenced to 298 K and
1 atm.
Enthalpy of Reaction
To get an enthalpy of reaction rH° we can measure the enthalpies of formation of the reactants and
products fH° and then take the difference between them as
rH° = fH°products- fH°reactants
For example, we can compute the enthalpy of the reaction
anhydrite + water = gypsum:
CaSO4 + 2H2O = CaSO4 2H2O
from
Ca + S + 2O2 = CaSO4 fH° = -1434.11 kJ/mol
H2 + 0.5O2 = H2O fH° = -285.830 kJ/mol
Ca + S + 3O2 + 2H2 = CaSO4 2H2O fH° = -2022.63 kJ/mol
Thus,
rH° = fH°gypsum - fH°anhydrite - fH°water = -16.86 kJ/mol.
Exothermic vs. Endothermic

41. If rH° < 0 the reaction produces a reduction in enthalpy and is exothermic (heat is given up by the rock
and gained by the surroundings). If rH° > 0 the reaction produces an increase in enthalpy and is
endothermic (heat from the surroundings is consumed by the rock). An easy way to remember this is
that spontaneous reactions produce a decrease in internal energy, and because we know that
UP HP
a decrease in HP is also a decrease in UP.
Calculating fH° at Temperatures Other Than 298 K
So far we know how to calculate the change in enthalpy caused by heating and we know that we can get
enthalpies of formation from tables. What if we want to know the enthalpy of formation of a mineral at
a temperature other than 298 K?
We do this by calculating rCP for the reaction that forms the mineral of interest:
rCP = rCPproducts - rCPreactants
and then integrating. Thus, for example if we want to know fH° for quartz at 1000 K, we get
coefficients for the heat capacities of Si, O2 and SiO2:
compound a b c d
Si 31.778 5.3878E-4 -1.4654E5 -1.7864E2
O2 48.318 -6.9132E-4 4.9923E5 -4.2066E2
SiO2 104.35 6.07E-3 3.4E-4 -1070
for the reaction
Si + O2 = SiO2
and we calculate
a = 24.254
b = 6.2225E-3
c = -3.5E5
d = -470.7
and thus,
fH°1000 - fH°298 = CP dT = a*(1000-298) + b/2*(10002-2982) - c*(1000-1-298-1)
0.5 0.5
+2 d*(1000 -298 ) = 5.511 kJ/mol

42. This is the change in the enthalpy of formation that results from heating. We add this to the enthalpy of
formation at 298 K to get the enthalpy of formation at 1000 K:
fH°1000 =( fH°1000 - fH°298) + fH°298 = 5.511 - 910.700 = -905.2 kJ/mol
In other words, forming quartz from the elements at 1000 K yields slightly less heat than at 298 K.
Compare this with the change in enthalpy H°298-1000 that results from heating quartz from 298 K to
1000 K, which we calculated is 45.37 kJ/mol.
Entropy
We have discussed the intuitive statement that reactions probably proceed because the reactants can
decrease their internal energy by reacting. We also noted that internal energy scales with enthalpy,
suggesting that reactions might 'go' because of a decrease in enthalpy. However, we then noted that not
all reactions give off heat--some, such as the melting of ice, proceed in spite of consuming heat.
Moreover, there are other processes that proceed in the apparent absence of any heat change: e.g.,
mixing of gases or the spreading of dye in water. What is it that causes these reactions to proceed
spontaneously even if the heat change is zero or endothermic?
The answer is entropy S, which is a measure of the order or disorder. Entropy has three sources:
configurational, electronic, and vibrational.
Configurational entropy refers to the entropy resulting from imperfect mixing of different
atoms in the same site in a crystal, and is described by the Boltzmann distribution:
Sconfigurational = k ln (This is engraved on Boltzmann's tomb in Vienna!)
where is the probability that a given number of atoms in a given number of sites will have a particular
configuration.
For N atomic sites that can contain fraction XA A atoms and XB B atoms,
=

43. N is always large where moles of material are concerned, so we can simplify this (using Stirling's
approximation) to
S = - n R (XA ln XA + XB ln XB)
where n is the number of sites per mole. For example in cordierite there are 4 Al atoms and 5 Si atoms
distributed over 9 tetrahedral sites. For a random distribution the entropy is
S = - 9 R (4/9 ln 4/9 + 5/9 ln 5/9) = 51.39 J mol-1 K-1
Note that the form of the configurational entropy equation (and electronic entropy as well) indicates
that if XA or XB are 0 or 1, Sconfig is zero:
Electronic entropy arises when an electron in an unfilled orbital can occupy more than one orbital; e.g.,
for Ti3+, the single 3d electron can occupy one of three possible t2g orbitals and Selectronic = 9 J mol-1 K-1.
Vibrational (or calorimetric) entropy arises because the energy of lattice vibrations can only increase or
decrease in discrete steps and the energy quanta (phonons) can be distributed within the possible
energy steps in different ways. Vibrational entropy is very difficult to calculate from statistical mechanics
but can be calculated easily from heat capacity. Here's why:
The entropy of a system always increases during irreversible processes; i.e., for a reversible process, dS =
0, whereas for irreversible processes dS >0. This is the Second Law of Thermo--better known as "You
can't feed s**t into the rear of a horse and get hay out the front."
If a mineral becomes more ordered during a reaction, reducing its entropy, the heat liberated must
increase the entropy of the surroundings by an even greater amount. Thus, we write
dS >
then

44. >
and recalling that
CP =
then
>
and
S= dT
In other words, the vibrational entropy can be found by integrating the heat capacity divided by
temperature.
In a perfectly ordered, pure crystalline material the entropy is zero. This is a simple statement of the
Third Law of Thermo, which follows from the fact that heat capacities approach zero at zero K:
C=0
However, because the rate of atomic diffusion also goes to zero at 0 K, all compounds have some zero-
point entropy S°0.
Entropy is thus the only thermodynamic potential for which we can calculate an absolute value. What
we typically do is determine the heat capacity from near absolute zero to ambient conditions and then
integrate it to get the (absolute) entropy (in fact this gives us only the vibrational entropy and ignores
configurational and electronic contributions to entropy).

45. Entropy Change of Reaction
Just like rH and rV, we can calculate entropies of reactions by using absolute entropies S and
calculating a difference in entropy rS. For example, if we know that
S°CaSO4 = 106.7 J mol-1 K-1
S°Ca = 41.42 J mol-1 K-1
S°S = 31.80 J mol-1 K-1
S°O2 = 205.138 J mol-1 K-1
then the entropy of the reaction
Ca + S + 2O2 = CaSO4
is rS° = 106.7 - 41.42 - 31.80 - 2 * 205.138 = -376.8 J mol-1 K-1

46. Energy Associated With Entropy
The units of entropy suggest that the energy associated with S scales with temperature:
dU -TS
(The minus sign is there for reasons similar to the -PV we encountered earlier.)
The energy associated with configurational entropy in the Al4Si5 cordierite we talked about earlier looks
like this:
The energy associated with vibrational entropy in tremolite, quartz, and chalcopyrite looks like
this:
(Josiah Willard) Gibbs Free Energy of a Phase
The Gibbs free energy G is the thermodynamic potential that tells us which way a reaction goes at a
given set of physical conditions--neither the enthalpy change nor the entropy change for a reaction

47. alone can provide us with this information. The two measures of energy (enthalpy H and entropic
energy TS) are brought together in the Gibbs free energy equation: (the chemical potential is the
equivalent for a component)
G = U + PV - TS
which says that the Gibbs free energy G is the internal energy of the crystal U plus the energy the crystal
gains by virtue of not being allowed to expand minus the entropic energy TS. Recalling that
H = U + PV
we can write this in a more understandable way
G = H - TS
which says that G is the difference between the heat energy and the entropic energy.
Relationship Among G, S, and V
If we differentiate
G = U + PV - TS
to obtain
dG = dU + PdV + VdP - TdS - SdT
and substitute

48. TdS = dU + PdV
(this comes from dS = dQ/T and dU = dQ - PdV); we are left with
dG = VdP - SdT
meaning that changes in Gibbs free energy are produced by changes in pressure and temperature acting
on the volume and entropy of a phase.
Realize that when we write
dG = VdP - SdT
we are implicitly writing
dG = dP - dT
which means that
=V
and
= -S

49. These relations indicate that the change in Gibbs free energy with respect to pressure is the molar
volume V and the change in Gibbs free energy with respect to temperature is minus the entropy S.
Gibbs Free Energy of Formation
The defining equation for Gibbs free energy
G = H - TS
can be written as
G= H-T S
such that the Gibbs free energy of formation fG° is
fG° = fH° -T fS°
For example, to calculate the Gibbs free energy of formation of anhydrite, we can use
fH°CaSO4 = -1434.11 kJ/mole
S°CaSO4 = 106.7 J mol-1 K-1
S°Ca = 41.42 J mol-1 K-1

50. S°S = 31.80 J mol-1 K-1
S°O2 = 205.138 J mol-1 K-1
and we calculate the entropy of formation of anhydrite
fS° = S°CaSO4 - S°Ca - S°S - 2 * S°O2 = -376.796 J mol-1 K-1
and then use
fG° = fH° -T fS° = -1434,110 - 298.15 * -376.796 = -1321.77 kJ/mol
Gibbs Free Energy of Reaction
We can write the Gibbs free energy of reaction as the enthalpy change of reaction minus the entropic
energy change of reaction
rG = rH -T rS
If the heat energy equals the entropic energy
rH =T rS
then
rG =0
and there is no reaction. Finally we have come to a satisfying point--we can now determine whether a
given reaction will occur if we know H and S, and both of these are measurable or can be
calculated.

51. If rG < 0, the Gibbs free energy of the products is lower than the Gibbs free energy of the reactants
and the reaction moves to produce more products. If rG > 0, the Gibbs free energy of the products is
greater than the Gibbs free energy of the reactants and the reaction moves to produce more reactants.
For example, to calculate rG° at STP for the reaction
aragonite = calcite
we use
rH° = 370 J
rS° = 3.7 J mol-1 K-1
to calculate
rG° = 370 - 298.15 * 3.7 = -733 J/mol
The negative value of G tells us that calcite has lower Gibbs free energy and that the reaction runs
forward (aragonite calcite).
Clapeyron Relation
There is a useful relation between the slope of a reaction in PT space (i.e., dP/dT) and the entropy and
volume changes of the reaction that follows from
rG = VrdP - SrdT
At equilibrium G = 0, such that

52. rVdP = rSdT
or
=
So, the P-T slope of a reaction is equal to the ratio of the entropy change to the volume change.
Alternatively, along the equilibrium curve, the changes in pressure times the volume change are equal to
changes in temperature times the entropy change. This is the Clapeyron Equation.
So, a phase diagram is a kind of free energy map. = along an equilibrium, < at
high P and low T, and > at high T and low P. Along the equilibrium boundary the Gibbs
Free energies of the reactants and products are equal and the Gibbs Free energy of reaction rG,
is zero.
Shortcutting H and S and Finding G Directly
Like other thermodynamic potentials, we can write the change in Gibbs free energy of reaction as
rG° = fG°reactants- fG°products
Instead of using fH° and fS°, it is often possible to obtain fG° values for most compounds from
electronic data bases. For example, if the following Gibbs free energies of formation are known:
fG°CaSO4 = -1707.280 kJ/mol
2H2O
fG°CaSO4 = -1321.790 kJ/mol
fG°H2O = -237.129 kJ/mol

53. then for
CaSO4 + 2H2O = CaSO4 2H2O
rG° = -1.232 kJ/mol
Gibbs Free Energy at Any Pressure and Temperature
We know many ways to determine rG at STP--but how do we calculate rG for other pressures and
temperatures? Recall that the changes in Gibbs free energy with pressure and temperature are given by
two of Maxwell's relations
= rV and =- rS
If we recast these as
= rV P
and
=- rS T
and integrate, we get
rGdP = rGP - rGPref = rVdP
or
rGP = rGPref + rVdP
and
rGdT = rGT - rGTref =- rSdT
or
rGT = rGTref - rSdT
thus
rGPT = rGPrefTref + rVdP - rSdT
Solving the Pressure Integral at Constant Temperature
To a first approximation, we can ignore the expansivity and compressibility of solids and use

54. rVsdP = rVs(P - 1)
as a simplification. Don't forget that this approximation is valid for solids only! An even more common
assumption for P>>1 is
rVsdP = rVsP
For example, calculate the change in Gibbs free energy for the reaction
2 jadeite = albite + nepheline
if pressure increases from 1 bar to 10 kbar, given
nepheline = 54.16 cm3
3
albite = 100.43 cm
3
jadeite = 60.40 cm
First we calculate rV and find
r = nepheline + albite -2 jadeite = 33.79 cm3 = 3.379 J/bar
and thus
rGPT - rG1,T = rVsP = 33.79 kJ/mol
Solving the Temperature Integral at Constant Pressure
Recall that the effect of temperature on the entropy change of reaction rS depends on the heat
capacity change of reaction rCP:
rS = dT
Thus
rGT = rGTref - rSdT
expands to
rGT = rGTref - STref + dT dT
If the form of the heat capacity expansion is

55. CP = a + bT + cT-2 + dT-0.5
then the above double integral is
a(T - T ln T) - bT2/2 - cT-1/2 + 4 dT0.5 - aTref - bTref2/2 + cTref-1 - 2 dTref0.5 +
aTlnTref + bTTref - cTTref-2/2 - 2 dTTref-0.5 - T rSTref + Tref rSTref
Note that this considers only vibrational entropy and ignores configurational entropy. This means of
solving for rG requires that you know rG at the reference temperature.
An alternative path that requires that you know the enthalpy change rH at the reference temperature
is
rGT = rHTref + CPdT - T rSTref + dT
Solving the Temperature and Pressure Integrals for rGP,T
To calculate the Gibbs free energy change of a reaction at any pressure and temperature, we can use
either of the following equations, depending on whether we know rH or rG
rGP,T = rG1,Tref - rSTref + dT dT + rVsP
rGP,T = rH1,Tref + CPdT - T rSTref + dT + rVsP
If you don't have heat capacity data for the reaction of interest, these equations can be roughly
approximated as
rGP,T = rG1,Tref - rS1,Tref(T - Tref) + rVsP
rGP,T = rH1,Tref - T rS1,Tref + rVsP
For example, calculate rG for jadeite + quartz = albite at 800 K and 20 kbar. The data at 298 K and 1
bar are
rH° = 15.86 kJ/mol
-1 -1
rS° = 51.47 J K mol
3
rVs° = 1.7342 J/bar = 17.342 cm /mol
Using
rGP,T = rH1,Tref - T rS1,Tref + rVsP
= 15,860 - 800 * 51.47 + 1.7342 * 20,000 = 9.37 kJ/mol
If we had used the complete equation for solids, integrating the heat capacities, we would have
obtained an answer of 9.86 kJ/mol--not horrifically different.

56. Calculating the PT Position of a Reaction
If we say that rG = 0 at equilibrium, then we can write our solids-only and constant-heat-capacity
approximations as
0= rG1,T - rS1,Tref(T - Tref) + rVsP
0= rH1,Tref -T rS1,Tref + rVsP
and thus we can calculate the pressure of a reaction at different temperatures by
P= rG1,Tref - rS1,Tref(T - Tref) /- rVs
P= rH1,Tref -T rS1,Tref /- rVs
and we can calculate the temperature of a reaction at different pressures by
T = Tref + rG1,Tref + rVsP / rS1,Tref
T = Tref + rH1,Tref + rVsP / rS1,Tref
Let's do this for the albite = jadeite + quartz reaction at T = 400 K and T = 1000 K:
P = (15,860 - 5147 * 400) / -1.7342 = 2.7 kbar
P = (15,860 - 5147 * 1000) / -1.7342 = 20.6 kbar
Assuming that dP/dT is constant (a bad assumption, we know), the reaction looks like this
Introduction to the Equilibrium Constant
A bit farther down the road we will encounter a monster called the equilibrium constant K:
K = exp(- rG°/RT)

57. or
ln K = - rG°/RT
At equilibrium, where rG°= 0, ln K = 0 and K = 1. Let's see what K looks like for jadeite + quartz = albite
at 800 K and 20 kbar:
ln K = - ( rH1,Tref - T rSTref + rVsP)/ RT
= -(15,860 - 800 * 51.47 + 1.7342 * 20,000)/(8.314*800) = -1.4
If we do this for all of PT space, we can contour PT space in terms of lnK:
Solutions

58. Almost no phases are pure, but typically are mixtures of components. For example, olivine varies from
pure forsterite Mg2SiO4 to pure fayalite Fe2SiO4, and can have any composition in between--it is a solid
solution. We need a way to calculate the thermodynamic properties of such solutions.
As a measure of convenience, we use mole fraction to describe the compositions of phases that are solid
solutions. For example, a mix of 1 part forsterite and 3 parts fayalite yields an olivine with 25 mol%
forsterite and 75 mol% fayalite, which can be written as (Mg0.25Fe0.75)2SiO4 or fo25fa75, etc. Mole fractions
are denoted as Xi.
We need a way of splitting up the Gibbs free energy of a phase among the various components of the
phase--how for example do we decide how much of the Gibbs free energy of an olivine is related to the
forsterite component and how much derives from the fayalite component? Likewise, how does the
Gibbs free energy of a phase vary with composition--is the relationship linear between endmembers??
We address these issues by defining a partial Gibbs free energy for each component at constant
pressure and temperature and constant composition of other components, called the partial molar
Gibbs free energy or chemical potential
i =
where n is the amount of substance. For olivine solid solution composed of fayalite and forsterite
components or endmembers, we write
dG = dnfayalite + dnforsterite
Volume of Mixing
Imagine that mole fractions of phase A and phase B with molar volumes VA and VB, are mixed together.
We can describe the volume of the mixture as
V = XAVA° + XBVB°
and it is a linear mixing of the two endmember volumes. We call this ideal mixing or mechanical mixing.
Real solutions, however, do not behave this way, and the mixing is always non ideal, although
sometimes only weakly so. The figure shows mixing that produces a smaller volume than expected, but
it is not possible to predict the shapes and positions of such mixing curves.

59. Partial Molar Volume
The partial molar volume is defined as
i
If you mix two compounds A and B together and find a volume of mixing that is non-ideal, how can you
determine the contribution that A and B each make to the volume? That is, what are the partial molar
volumes of A and B, A and B?? Graphically, the partial molar volumes are the A and B axis intercepts
of the tangent to the mixing curve, and can be described by the simple relationship:
Vmix = XA A + XB B
or
Vmix = Xi i
The behavior of this function is such that when XA is 1, Vmix = VA and when XA is 0, Vmix = VB. Alternatively,

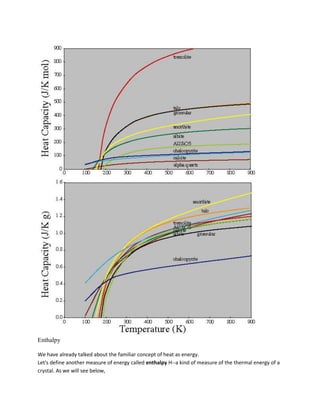
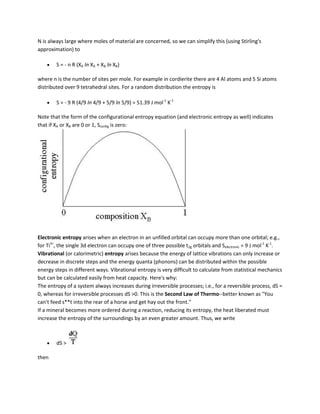
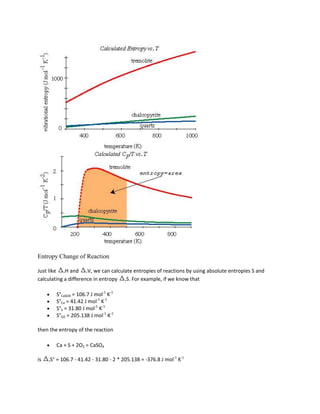
60. A = (Vmix - XB B) / XA
Entropy of Mixing
The entropy of mixing is never zero because mixing increases entropy. As we discussed days ago, the
entropy of mixing (i.e., the configurational entropy) is
Smix = -R (Xi ln Xi)
where i = 1..n is the number of sites over which mixing is occurring.
Enthalpy of Mixing
Enthalpies also do not combined ideally (linearly) in mixtures because the mixture may have stronger
bonds than were present in either of the unmixed phases. The excess enthalpy is
Hmix = 0.5 * N z XAXB [2 AB - AA - BB]
where AB is the interaction energy among A-B atoms, AA is the interaction energy among A-A atoms,
and BB is the interaction energy among B-B atoms.
Gibbs Free Energy of Mixing
Recall that all spontaneous processes/reactions occur because of a decrease in Gibbs free energy. It
should therefore not surprise you that the Gibbs free energy of mixing is always negative--otherwise
mixing would not occur. The fact that A < G°A and B < G°B illustrates why compounds combine
spontaneously--each compound is able to lower its free energy.

61. The above figure is hypothetical because we cannot measure or calculate the absolute Gibbs free
energy of phases. For this reason, is always expressed as a difference from some standard state
measurement, as , - °, or - G°.
The difference between the absolute Gibbs free energy G° per mole ° of a pure compound and
the chemical potential per mole of dissolved compound is
A - G°A = A - °A = RT lnXA
This function has the following shape:

62. implying that when the mineral is pure (X = 1) then = 0, and when the mineral is infinitely
dilute (X = 0) then the chemical potential is undefined. For example, in a two-component
mineral if XA = 0.4, at T = 298 K,
A- °A = 8.314 * 298 ln 0.4 = -2271 J
B- °B = 8.314 * 298 ln 0.6 = -1266 J
The equation of the Gmix line is the sum of the chemical potentials of the endmembers:
Gmix = RT (XA ln XA + XB ln XB) or
Gmix = RT (Xi ln Xi)
which looks like this for two components:
Actually, all this discussion has been predicated on the assumption that Hmix = 0. If this is not
true, Gmix is not a simple function of composition, but has the general form:

63. Depending on the relative values of Hmix and -T Smix, the free energy of mixing may be
negative throughout the whole composition range if the entropic energy contribution outweighs
the enthalpy increase; this is more likely at higher temperature.
The two free energy minima in the above figure indicate that minerals of intermediate
compositions can reduce their free energy by unmixing into two phases. This explains the
appearance and driving force for exsolution. Note that this can only be true if Hmix > 0, i.e., if
2 AB > AA + BB, which makes sense because it means that the A-B bonds have a higher free
energy than the sum of the free energies of separate AA and BB bonds.
Activities
In reality, no phases behave ideally--that is, their chemical potentials are never simple logarithmic
functions of composition as
A - °A = RT lnXA
implies. Instead, we say that the chemical potential is a simple logarithmic function of activity and
define activity as
a = ( X)
where a is the activity of a compound, is the "site occupancy coefficient" (e.g., = 2 for Mg in
Mg2SiO4), and is the activity coefficient that describes the non-ideal behavior. Thus we write
A - °A = RT lnaA
For pure compounds a=1 because X=1. For ideal compounds =1. As a specific example, the chemical
potential of the almandine (Fe3Al2Si3O12) component of a garnet solid solution ((Fe, Mg, Ca,
Mn)3Al2Si3O12) is
alm = °alm + RT lnXalm

64. To be clear, ° is the chemical potential of the component in its pure reference state and varies as a
function of pressure and temperature; this we measure with calorimetry. is the chemical potential as
it actually occurs and varies as a function of phase composition; this we measure with an electron
microprobe. The activity forms a bridge between idealized behavior and real behavior.
The Equilibrium Constant
At equilibrium the sum of the Gibbs free energies of the reactants equals the sum of the Gibbs free
energies of the products. Equally, the sum of the partial molar Gibbs free energies (chemical potentials)
of the reactants equals the sum of the partial molar Gibbs free energies (chemical potentials) of the
products. In other words, for
SiO2 + 2H2O = H4SiO4
at equilibrium,
H4SiO4 = SiO2 + 2 H2O
More generally, for
aA + bB = cC + dD
then
c C+d D=a A+b B
or, at equilibrium
r =0=c C+d D-a A-b B
which we can reformat as
r = i i
where i is the stochiometric coefficient of a product or reactant and is positive if for a product and
negative if for a reactant. If we then remember that
- ° = RT lna
and rewrite it as
= ° + RT lna
we can reformat the earlier equation as

65. r = 0 = c( C° + RT lnaC) + d( D° + RT lnaD) - a( A° + RT lnaA) - b( B° + RT lnaB)
which looks nicer as
r = r ° + RT ln (aCc aDd/aAa aBb)
To be completely general we write
r = r ° + RT ln ai ( means to multiply all i terms)
This equation is invariably simplified to
r = r ° + RT lnQ
and Q is the activity product ratio. The activities in the Q term change as the reaction progresses toward
equilibrium.
To be clear again, r ° is the difference in the Gibbs free energies of the products and reactants when
each is in its pure reference state and varies as a function of pressure and temperature. r is the
difference in the Gibbs free energies of the products and reactants as they actually occur and varies as a
function of phase composition.
At equilibrium, the product and reactant activities have adjusted themselves such that r = 0. We
write this (with K instead of Q, to signify equilibrium) as
0= rG° = -RT ln K
K is called the equilibrium constant. If K is very large (ln K positive), the combined activities of the
reaction products are enormous relative to the combined activities of the reactants and the reaction will
likely progress. On the other hand, if K is small (ln K negative), there is unlikely to be any reaction.
The utility of K is that it tells us for any reaction and any pressure and temperature, what the activity
ratios of the phases will be at equilibrium. For example, for the reaction
albite = jadeite + quartz
let's say that at a particular P and T,
rG° = -20.12 kJ/mol
Using
rG° = -RT lnK
we calculate

66. log K = 3.52
This means that at equilibrium,
(ajadeite aquartz / aNaAlSi3O8) = e3.52
Where ajadeite is the activity of NaAlSi2O6 in clinopyroxene and aalbite is the activity of NaAlSi3O8 in
plagioclase.
Alternative Route to the Equilibrium Constant
When we think of mass balance in a reaction, we can explicitly write
0= iMi
where i are the stoichiometric coefficients and Mi are the masses or the phase components.
Analogously, we can explicitly write a similar balance among the chemical potentials:
0= i i
For each chemical potential we can write
i= °i + RT lnai
Combining these two equations we find
0= i °i + iRTln ai
0= i °i + RTln (ai)
0= i °i + RTln ai
0= i °i + RTln K
and eventually
0= rG° + RT ln K
or
rG° = -RT ln K
The equation
K= ai

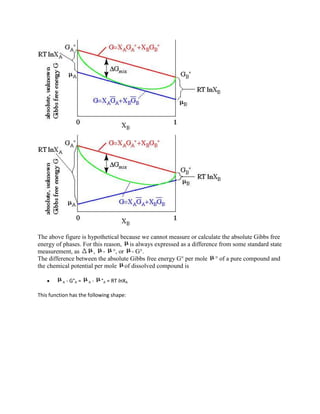
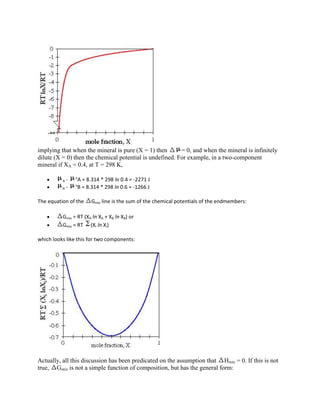
67. is the law of mass action (which actually discusses the action of chemical potential rather than mass).
We can also write for 298 K and 1 atm
rH° -T rS° = - RT ln K
and for any P and T of interest:
rH1,Tref + CPdT - T rSTref + dT + rVP = - RT ln K
This has been called "the most important equation in thermodynamics," so you'd better like it(!) The
equilibrium constant K is a function of 1/T
-ln K = ( rG° / RT) = [( rH / RT) - ( rS / R)]
Which looks like
Activity Models (Activity-Composition Relations) for Crystalline Solutions
Garnets are solid solutions of
component abbrev. Formula
pyrope prp Mg3Al2Si3O12
almandine alm Fe3Al2Si3O12
grossular grs Ca3Al2Si3O12
spessartine sps Mn3Al2Si3O12
andradite and Ca3Fe23+Si3O12
Mixing models derive from entropy considerations. In particular the relation

68. Smix = -R Xi ln Xi
although we will not go through the derivation.
Mixing on a Single Site
The simplest type of useful activity model is the ionic model, wherein we assume that mixing occurs on
crystallographic sites. For a Mg-Fe-Ca-Mn garnet with mixing on one site, which we can idealize as
(A,B,C,D) Al2Si3O12, the activities are
3 3
aprp = Mg XMg
3 3
aalm = Fe XFe
3 3
agrs = Ca XCa
3 3
asps = Mn XMn
The pyrope activity is shown in the above figure.
In general, for ideal mixing in a mineral with a single crystallographic site that can contain
ions,
ai = Xj
where a, the activity of component i, is the mole fraction of element j raised to the power. For non-
ideal mixing, we include an activity coefficient
ai = j Xj
Mixing on a Several Sites
For minerals with two distinct sites and the general formula
(A,B) (Y,Z)

69. there are four possible end member components A Y , A Z , B Y , and B Z .
The ideal activities of these components are
aA Y = XA XY
aA Z = XA XZ
aB Y = XB XY
aB Z = XB XZ
For non-ideal garnet activities we write
aprp = XMg3 XAl2 or Mg3 XMg3 Al2 XAl2
aalm = XFe3 XAl2 or Fe3 XFe3 Al2 XAl2
agrs = XCa3 XAl2 or Ca3 XCa3 Al2 XAl2
asps = XMn3 XAl2 or Mn3 XMn3 Al2 XAl2
aand = XCa3 XFe3+2 or Ca3 XMn3 Fe3+2 XFe3+2
where the X3 term describes mixing on the 8-fold trivalent site and the X2 term describes mixing on the
octahedral divalent site.
The pyrope activity is shown in the above figure for Mg from 0 3 and Al from 0 2.
It is common to modify such models that are based on completely random mixing of elements
with models that consider local charge balance on certain sites or the Al-avoidance principle.
Geothermometry and Geobarometry
Exchange Reactions
Many thermometers are based on exchange reactions, which are reactions that exchange elements but
preserve reactant and product phases. For example:

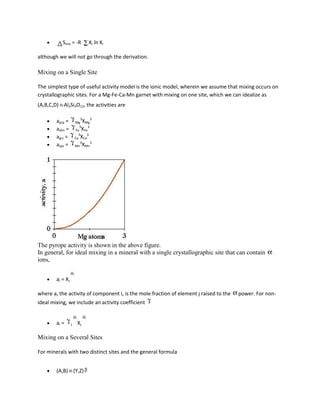
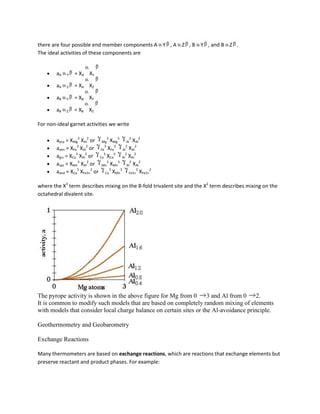
70. Fe3Al2Si3O12 + KMg3AlSi3O10(OH)2 = Mg3Al2Si3O12 + KFe3AlSi3O10(OH)2
almandine + phlogopite = pyrope + annite
We can reduce this reaction to a simple exchange vector:
(FeMg)gar+1 = (FeMg)bio-1
Popular thermometers include garnet-biotite (GARB), garnet-clinopyroxene, garnet-hornblende, and
clinopyroxene-orthopyroxene; all of these are based on the exchange of Fe and Mg, and are excellent
thermometers because rV is small, such that
=
is large (i.e., the reactions have steep slopes and are little influenced by pressure). Let's write the
equilibrium constant for the GARB exchange reaction
K = (aprpaann)/(aalmaphl)
thus
rG = -RT ln (aprpaann)/(aalmaphl)
This equation implies that the activities of the Fe and Mg components of biotite and garnet are a
function of Gibbs free energy change and thus are functions of pressure and temperature.
If we assume ideal behavior ( = 1) in garnet and biotite and assume that there is mixing on only 1 site
aalm = Xalm3 = [Fe/(Fe + Mg + Ca + Mn)]3
aprp = Xprp3 = [Mg/(Fe + Mg)]3
aann = Xann3 = [Fe/(Fe + Mg)]3
aphl = Xphl3 = [Mg/(Fe + Mg)]3
Thus the equilibrium constant is
K = (XMggar XFebio)/(XFegar XMgbio)
When discussing element partitioning it is common to define a distribution coefficient KD, which is just
the equilibrium constant without the exponent (this just describes the partitioning of elements and not
the partitioning of chemical potential):
KD = (XMggar XFebio)/(XFegar XMgbio) = (Mg/Fe)gar /(Mg/Fe)bio = K1/3

71. Long before most of you were playground bullies (1978) a couple of deities named John Ferry and Frank
Spear measured experimentally the distribution of Fe and Mg between biotite and garnet at 2 kbar and
found the following relationship:
If you compare their empirical equation
ln KD = -2109 / T + 0.782
this immediately reminds you of
ln K = - ( rG° / RT) = -( rH / RT) - (P rV / RT) + ( rS / R)
and you realize that for this reaction
rS = 3*0.782*R = 19.51 J/mol K
(the three comes from the site occupancy coefficient; i.e., K = KD3) and
-( rH / R) - (P rV / R) = -2109
or
rH = 3*2109*R -2070* rV
Molar volume measurements show that for this exchange reaction rV = 0.238 J/bar, thus
rH = 52.11 kJ/mol
The full equation is then

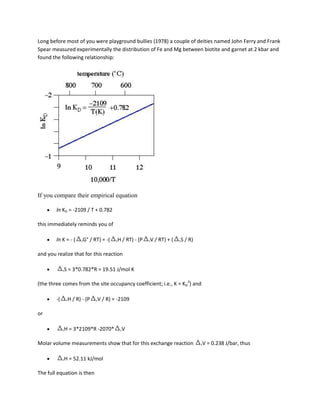
72. 52,110 - 19.51*T(K) + 0.238*P(bar) + 3RT ln KD = 0
To plot the KD lines in PT space
Net-Transfer Reactions
Net-transfer reactions are those that cause phases to appear or disappear. Geobarometers are often
based on net-transfer reactions because rV is large and relatively insensitive to temperature. A
popular one is GASP:
3CaAl2Si2O8 = Ca3Al2Si3O12 + 2Al2SiO5 + SiO2
anorthite = grossular + kyanite + quartz
which describes the high-pressure breakdown of anorthite.
For this reaction
rG = -RT ln [(aqtzaky2agrs) / aan3] = -RT ln agrs / aan3
(the activities of quartz and kyanite are one because they are pure phases). A best fit through the
experimental data for this reaction by Andrea Koziol and Bob Newton yields
P(bar) = 22.80 T(K) - 7317
for rV = -6.608 J/bar. Again, if we use

73. ln K = -( rH / RT) - (P rV / RT) + ( rS / R)
and set ln K = 0 to calculate values at equilibrium, we can rewrite the above as
(P rV / R) = -( rH / R) + (T rS / R)
or
P=T rS / rV - rH / rV
if T rS / rV = 22.8 then rS = -150.66 J/mol K
if rH / rV = 7317 then rH = -48.357 kJ/mol
So, we can write the whole shmear as
0 = -48,357 + 150.66 T(K) -6.608 P (bar) + RT ln K
Contours of ln K on a PT diagram for GASP look like this:
Kinetics
Thermodynamics places no constraints on the rate or mechanism of reaction--that is the realm of
kinetics. A popular method for describing the rate at which reactions proceed is to talk of an activated
state through which the reaction must pass:

74. When a system passes from an initial to a final state it must overcome an activation energy
barrier G*.
The advantages of this activation energy barrier paradigm are that it qualitatively explains the
i) persistence of metastable states; ii) effect of catalysts in lowering G*; iii) temperature
dependence of transformation. We can draw a similar diagram for a change in enthalpy induced
by the reaction rH and an activation enthalpy barrier H* (usually called an activation
energy Q*). Of course, unlike rG, rH can be positive or negative:
It is not easy to generalize about the activation entropy S*, however, in general, reactions with
positive entropy change rS are faster. For example, evaporation is faster than condensation,
melting is faster than crystallization, and disordering is faster than ordering.
Because thermal energy dictates whether an atom has sufficient energy to overcome an
activation energy barrier, we will write that the fraction of atoms with thermal energy greater
than H* is
f = exp ( - H*/RT)

75. i.e., if f << 1, few atoms have enough thermal energy to overcome the activation energy barrier,
whereas if f = 1 all atoms can overcome the activation energy barrier.
For reactions that involve a single step characterized by a single activation energy, the rate of the
reaction depends on the i) frequency with which atoms attempt to jump from one site to the next
; ii) fraction of atoms with thermal energy greater than Q*; and iii) probability p that the atom
jumping satisfies some geometrical consideration (this is a fancy name for a fudge factor):
rate p exp(-Q*/RT)
Often this is rewritten as rate (kT/h) exp(-Q*/RT)
where k is Boltzmann's constant, and h is Planck's constant. Thus, the rate at which atoms jump is
related to temperature and to atom-scale processes described by k and h.
Nucleation
Most transformations take place by nucleation and growth. The driving force for nucleation results from
the fact that the formation of the new phase lowers the total free energy by VG, the Gibbs free
energy change of reaction per unit volume. Nucleation is opposed by an interfacial energy and a
strain energy . The overall change in nucleation energy for a spherical nucleus of radius r is then
nG = VG + Ginterfacial + Gstrain = (4/3) r3 VG + 4 r2 + (4/3) r3
These different energy contributions yield an increase in total free energy up to a certain radius termed
the critical radius, beyond which the total free energy decreases.

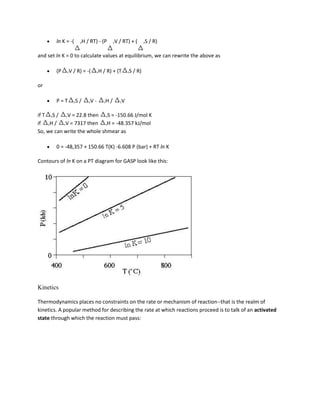
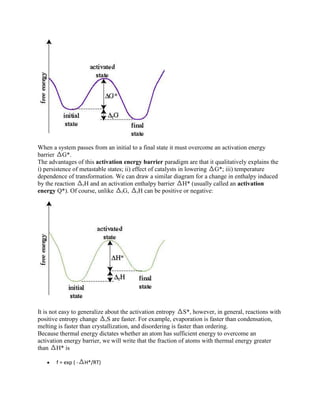
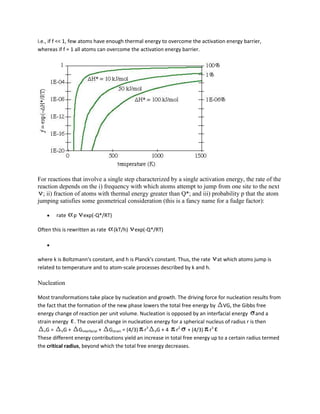
76. This change from increasing to decreasing nucleation free energy happens because the
surface:volume ratio decreases with increasing radius, so the negative volume free energy term
that favors nucleation eventually overwhelms the positive surface and strain free energy terms
that oppose nucleation. We can re-order the terms in the above equation to calculate the critical
size of the nucleus rc
rc = -2 /( VG + )
If, at the critical radius, nG = G*, the activation energy for nucleation is
3
G* = 16 / 3( VG + )2
Growth
Following nucleation, grains of the product phase(s) grow to replace the parent phase(s). Either the
reaction is polymorphic, or atoms of the parent phase must dissolve, be transported, and then attach
themselves to the product phase. The rate of growth is thus controlled by the rate of the slowest of
these three steps, and is described as either interface controlled or diffusion controlled.
Turnbull's (1956) formulation to quantify interface-controlled growth rate is:
= (kT/h) exp( -Q*/RT)[( - rG/RT)]
where is an "interface jump distance" and the rest you will recognize from previous equations. The [( -
rG/RT)] term indicates that the rate of growth depends on the Gibbs free energy change of reaction.
As rG 0, this term also approaches zero. As rG , this term approaches 1.
Transformation: Nucleation + Growth

77. A complete transformation involves nucleation and growth--the product phases must form and grow
and the parent phases must be consumed. The letter _ is often used to indicate 'reaction progress' or
'degree of transformation,' and varies from 0 (no reaction) to 1 (complete reaction). The transformation
is the time-integrated result of ongoing nucleation and growth, which can vary in time and space:
= 1 - exp[(4/3) dt]
Just as an example, the general rate equation for interface-controlled (i.e., not diffusion-controlled)
growth of nuclei formed on grain boundaries is
2
= 1 - exp{(6.7/d) [1-exp( [ (t - )2 - y2] d )] dy}
In their simplest form, these equations have the form
= 1 - exp(-ktn)
Flip this around to
exp(-ktn) = 1 -
linearize by means of logarithms
-ktn = ln (1 - )
change signs and cleverly insert ln 1
ktn = ln 1 - ln (1 - )
rewrite the two logarithms as one, recalling that ln (a/b) = ln a - ln b
ktn = ln [1 / (1 - )]
and linearize once more with logarithms to get the final glorious equation
n ln t + ln k = ln [ ln (1 - )]
The Last Supper: A Still Life of Thermodynamics & Kinetics
Zeolites, like laumontite and wairakite, form in oil fields as alteration products of plagioclase and other
Ca-bearing phases. The thermodynamic properties ( H, S, V, CP) of zeolites have been measured, and
we can use those properties to calculate a phase diagram for the CASH system:

78. Laumontite is the phase that is stable at the lowest P and T. Wairakite is the next phase to form, and it
does so via the reaction laumontite _ wairakite + H2O. At higher temperature wairakite + H2O
decompose to anorthite + quartz + H2O.
Kinetic experiments conducted on the reaction laumontite _ wairakite + H2O, using crystals of
laumontite suspended in H2O, reveal the transformation vs. time data in the figure above.
One could use the equation
to interpret the two sub-figures to reveal different n and k values for each temperature. This is the way
rate data were interpreted in the bad old days, but this approach lacks any physical or mechanistic basis.
Instead, we can measure the rate of growth at each temperature and relate the rate of growth to the
Turnbull equation. Above is an example of grain growth data collected for 450°C. The rate of growth is
interpreted to be a constant 2.0 ± 0.3 E-10 m/s. If growth rate data like this can be collected for every
temperature of interest, an activation energy for growth can be calculated:
The activation energy for growth apparently varies from ~196 kJ/mol to ~ 72 kJ/mol depending on the
reaction mechanism. The growth rate data can be combined with similar nucleation rate data to yield a
complete transformation rate equation that can be extrapolated to geologic conditions of interest. The
figure below shows extrapolated growth rates (m/s) for the laumontite _ wairakite + H2O reaction.
search
Potentials
Free energy · Free entropy
Internal energy U(S,V)
Enthalpy H(S,p) = U + pV
Helmholtz free energy A(T,V) = U − TS
Gibbs free energy G(T,p) = H − TS
The four laws of thermodynamics define fundamental physical quantities (temperature, energy, and
entropy) that characterize thermodynamic systems. The laws describe how these quantities behave
under various circumstances, and forbid certain phenomena (such as perpetual motion).
The four laws of thermodynamics are:[1][2][3][4][5][6]

79. Zeroth law of thermodynamics: If two systems are in thermal equilibrium with a third system,
they must be in thermal equilibrium with each other. This law helps define the notion of
temperature.
First law of thermodynamics: Heat and work are forms of energy transfer. Energy is invariably
conserved but the internal energy of a closed system changes as heat and work are transferred
in or out of it. Equivalently, perpetual motion machines of the first kind are impossible.
Second law of thermodynamics: The entropy of any isolated system not in thermal
equilibrium almost always increases. Isolated systems spontaneously evolve towards thermal
equilibrium—the state of maximum entropy of the system—in a process known as
"thermalization". Equivalently, perpetual motion machines of the second kind are impossible.
Third law of thermodynamics: The entropy of a system approaches a constant value as the
temperature approaches zero. The entropy of a system at absolute zero is typically zero, and in
all cases is determined only by the number of different ground states it has. Specifically, the
entropy of a pure crystalline substance at absolute zero temperature is zero.
Classical thermodynamics describes the exchange of work and heat between systems. It has a special
interest in systems that are individually in states of thermodynamic equilibrium. Thermodynamic
equilibrium is a condition of systems which are adequately described by only macroscopic variables.
Every physical system, however, when microscopically examined, shows apparently random microscopic
statistical fluctuations in its thermodynamic variables of state (entropy, temperature, pressure, etc.).
These microscopic fluctuations are negligible for systems which are nearly in thermodynamic equilibrium
and which are only macroscopically examined. They become important, however, for systems which are
nearly in thermodynamic equilibrium when they are microscopically examined, and, exceptionally, for
macroscopically examined systems that are in critical states,[7] and for macroscopically examined systems
that are far from thermodynamic equilibrium.
There have been suggestions of additional laws, but none of them achieve the generality of the four
accepted laws, and they are not mentioned in standard textbooks.[1][2][3][4][5][8][9]
The laws of thermodynamics are important fundamental laws in physics and they are applicable in other
natural sciences.
Table of Contents
1 Zeroth law
2 First law
3 Second law
4 Third law
5 History
6 See also
7 References
8 Further reading
Zeroth law

80. The zeroth law of thermodynamics may be stated as follows:
If system A and system B are individually in thermal equilibrium with system C, then system A is in
thermal equilibrium with system B
The zeroth law implies that thermal equilibrium, viewed as a binary relation, is a Euclidean relation. If we
assume that the binary relationship is also reflexive, then it follows that thermal equilibrium is an
equivalence relation. Equivalence relations are also transitive and symmetric. The symmetric relationship
allows one to speak of two systems being "in thermal equilibrium with each other", which gives rise to a
simpler statement of the zeroth law:
If two systems are in thermal equilibrium with a third, they are in thermal equilibrium with each other
However, this statement requires the implicit assumption of both symmetry and reflexivity, rather than
reflexivity alone.
The law is also a statement about measurability. To this effect the law allows the establishment of an
empirical parameter, the temperature, as a property of a system such that systems in equilibrium with
each other have the same temperature. The notion of transitivity permits a system, for example a gas
thermometer, to be used as a device to measure the temperature of another system.
Although the concept of thermodynamic equilibrium is fundamental to thermodynamics and was clearly
stated in the nineteenth century, the desire to label its statement explicitly as a law was not widely felt
until Fowler and Planck stated it in the 1930s, long after the first, second, and third law were already
widely understood and recognized. Hence it was numbered the zeroth law. The importance of the law as
a foundation to the earlier laws is that it allows the definition of temperature in a non-conjugate variable.
First law
The first law of thermodynamics may be stated thus:
Increase in internal energy of a body = heat supplied to the body - work done by the body. U = Q
-W

81. For a thermodynamic cycle, the net heat supplied to the system equals the net work done by the
system.
More specifically, the First Law encompasses several principles:
The law of conservation of energy.
This states that energy can be neither created nor destroyed. However, energy can change
forms, and energy can flow from one place to another. The total energy of an isolated system
remains the same.
The concept of internal energy and its relationship to temperature.
If a system, for example a rock, has a definite temperature, then its total energy has three
distinguishable components. If the rock is flying through the air, it has kinetic energy. If it is high
above the ground, it has gravitational potential energy. In addition to these, it has internal energy
which is the sum of the kinetic energy of vibrations of the atoms in the rock, and other sorts of
microscopic motion, and of the potential energy of interactions between the atoms within the rock.
Other things being equal, the internal energy increases as the rock's temperature increases. The
concept of internal energy is the characteristic distinguishing feature of the first law of
thermodynamics.
The flow of heat is a form of energy transfer.
In other words, a quantity of heat that flows from a hot body to a cold one can be expressed as an
amount of energy being transferred from the hot body to the cold one.
Performing work is a form of energy transfer.
For example, when a machine lifts a heavy object upwards, some energy is transferred from the
machine to the object. The object acquires its energy in the form of gravitational potential energy
in this example.
Combining these principles leads to one traditional statement of the first law of thermodynamics: it is not
possible to construct a perpetual motion machine which will continuously do work without consuming
energy.
Second law
The second law of thermodynamics asserts the existence of a quantity called the entropy of a system and
further states that
When two isolated systems in separate but nearby regions of space, each in thermodynamic equilibrium
in itself (but not necessarily in equilibrium with each other at first) are at some time allowed to interact,
breaking the isolation that separates the two systems, allowing them to exchange matter or energy, they
will eventually reach a mutual thermodynamic equilibrium. The sum of the entropies of the initial, isolated
systems is less than or equal to the entropy of the final combination of exchanging systems. In the
process of reaching a new thermodynamic equilibrium, total entropy has increased, or at least has not
decreased.
It follows that the entropy of an isolated macroscopic system never decreases. The second law states
that spontaneous natural processes increase entropy overall, or in another formulation that heat can

82. spontaneously be conducted or radiated only from a higher-temperature region to a lower-temperature
region, but not the other way around.
The second law refers to a wide variety of processes, reversible and irreversible. Its main import is to tell
about irreversibility.
The prime example of irreversibility is in the transfer of heat by conduction or radiation. It was known long
before the discovery of the notion of entropy that when two bodies of different temperatures are
connected with each other by purely thermal connection, conductive or radiative, then heat always flows
from the hotter body to the colder one. This fact is part of the basic idea of heat, and is related also to the
so-called zeroth law, though the textbooks' statements of the zeroth law are usually reticent about that,
because they have been influenced by Carathéodory's basing his axiomatics on the law of conservation
of energy and trying to make heat seem a theoretically derivative concept instead of an axiomatically
accepted one. Šilahvý (1997) notes that Carathéodory's approach does not work for the description of
irreversible processes that involve both heat conduction and conversion of kinetic energy into internal
energy by viscosity (which is another prime example of irreversibility), because "the mechanical power
and the rate of heating are not expressible as differential forms in the 'external parameters'". [10]
The second law tells also about kinds of irreversibility other than heat transfer, and the notion of entropy
is needed to provide that wider scope of the law.
According to the second law of thermodynamics, in a reversible heat transfer, an element of heat
transferred, δQ, is the product of the temperature (T), both of the system and of the sources or
destination of the heat, with the increment (dS) of the system's conjugate variable, its entropy (S)
View formula on Wikipedia[1]
The second law defines entropy, which may be viewed not only as a macroscopic variable of classical
thermodynamics, but may also be viewed as a measure of deficiency of physical information about the
microscopic details of the motion and configuration of the system, given only predictable experimental
reproducibility of bulk or macroscopic behavior as specified by macroscopic variables that allow the
distinction to be made between heat and work. More exactly, the law asserts that for two given
macroscopically specified states of a system, there is a quantity called the difference of entropy between
them. The entropy difference tells how much additional microscopic physical information is needed to
specify one of the macroscopically specified states, given the macroscopic specification of the other,
which is often a conveniently chosen reference state. It is often convenient to presuppose the reference
state and not to explicitly state it. A final condition of a natural process always contains microscopically
specifiable effects which are not fully and exactly predictable from the macroscopic specification of the
initial condition of the process. This is why entropy increases in natural processes. The entropy increase
tells how much extra microscopic information is needed to tell the final macroscopically specified state
from the initial macroscopically specified state.[11]
Third law
The third law of thermodynamics is sometimes stated as follows:
The entropy of a perfect crystal at absolute zero is exactly equal to zero.
At zero temperature the system must be in a state with the minimum thermal energy. This statement
holds true if the perfect crystal has only one state with minimum energy. Entropy is related to the number
of possible microstates according to S = kBln(Ω), where S is the entropy of the system, kB Boltzmann's
constant, and Ω the number of microstates (e.g. possible configurations of atoms). At absolute zero there
is only 1 microstate possible (Ω=1) and ln(1) = 0.

83. A more general form of the third law that applies to systems such as glasses that may have more than
one minimum energy state:
The entropy of a system approaches a constant value as the temperature approaches zero.
The constant value (not necessarily zero) is called the residual entropy of the system.
History
See also: Philosophy of thermal and statistical physics
Count Rumford (born Benjamin Thompson) showed, about 1797, that mechanical action can generate
indefinitely large amounts of heat, so challenging the caloric theory. The historically first established
thermodynamic principle which eventually became the second law of thermodynamics was formulated by
Sadi Carnot during 1824. By 1860, as formalized in the works of those such as Rudolf Clausius and
William Thomson, two established principles of thermodynamics had evolved, the first principle and the
second principle, later restated as thermodynamic laws. By 1873, for example, thermodynamicist Josiah
Willard Gibbs, in his memoir Graphical Methods in the Thermodynamics of Fluids, clearly stated the first
two absolute laws of thermodynamics. Some textbooks throughout the 20th century have numbered the
laws differently. In some fields removed from chemistry, the second law was considered to deal with the
efficiency of heat engines only, whereas what was called the third law dealt with entropy increases.
Directly defining zero points for entropy calculations was not considered to be a law. Gradually, this
separation was combined into the second law and the modern third law was widely adopted.
ENERGY TRASFORMATION
Laws of Thermodynamics
Process functions:
Work · Heat
Material properties
T
Specific heat capacity c =
N
Compressibility β=−1

84. V ∂p
1
Thermal expansion α=
V
· Free entropy
Internal energy U(S,V)
Enthalpy H(S,p) = U + pV
Helmholtz free energy A(T,V) = U − TS
Gibbs free energy G(T,p) = H − TS
The four laws of thermodynamics define fundamental physical quantities (temperature, energy, and
entropy) that characterize thermodynamic systems. The laws describe how these quantities behave
under various circumstances, and forbid certain phenomena (such as perpetual motion).
The four laws of thermodynamics are:1][2][3][4][5][6]
Zeroth law of thermodynamics: If two systems are in thermal equilibrium with a third system, they must
be in thermal equilibrium with each other. This law helps define the notion of temperature.
First law of thermodynamics: Heat and work are forms of energy transfer. Energy is invariably conserved
but the internal energy of a closed system changes as heat and work are transferred in or out of it.
Equivalently, perpetual motion machines of the first kind are impossible.
Second law of thermodynamics: The entropy of any isolated system not in thermal equilibrium almost
always increases. Isolated systems spontaneously evolve towards thermal equilibrium—the state of
maximum entropy of the system—in a process known as "thermalization". Equivalently, perpetual
motion machines of the second kind are impossible.
Third law of thermodynamics: The entropy of a system approaches a constant value as the temperature
approaches zero. The entropy of a system at absolute zero is typically zero, and in all cases is
determined only by the number of different ground states it has. Specifically, the entropy of a pure
crystalline substance at absolute zero temperature is zero.
Classical thermodynamics describes the exchange of work and heat between systems. It has a special
interest in systems that are individually in states of thermodynamic equilibrium. Thermodynamic

85. equilibrium is a condition of systems which are adequately described by only macroscopic variables.
Every physical system, however, when microscopically examined, shows apparently random microscopic
statistical fluctuations in its thermodynamic variables of state (entropy, temperature, pressure, etc.).
These microscopic fluctuations are negligible for systems which are nearly in thermodynamic
equilibrium and which are only macroscopically examined. They become important, however, for
systems which are nearly in thermodynamic equilibrium when they are microscopically examined, and,
exceptionally, for macroscopically examined systems that are in critical states,[7] and for
macroscopically examined systems that are far from thermodynamic equilibrium.
There have been suggestions of additional laws, but none of them achieve the generality of the four
accepted laws, and they are not mentioned in standard textbooks.[1][2][3][4][5][8][9]
The laws of thermodynamics are important fundamental laws in physics and they are applicable in other
natural sciences.
Zeroth law
The zeroth law of thermodynamics may be stated as follows:
If system A and system B are individually in thermal equilibrium with system C, then system A is in
thermal equilibrium with system B
The zeroth law implies that thermal equilibrium, viewed as a binary relation, is a Euclidean relation. If
we assume that the binary relationship is also reflexive, then it follows that thermal equilibrium is an
equivalence relation. Equivalence relations are also transitive and symmetric. The symmetric
relationship allows one to speak of two systems being "in thermal equilibrium with each other", which
gives rise to a simpler statement of the zeroth law:
If two systems are in thermal equilibrium with a third, they are in thermal equilibrium with each other
However, this statement requires the implicit assumption of both symmetry and reflexivity, rather than
reflexivity alone.
The law is also a statement about measurability. To this effect the law allows the establishment of an
empirical parameter, the temperature, as a property of a system such that systems in equilibrium with
each other have the same temperature. The notion of transitivity permits a system, for example a gas
thermometer, to be used as a device to measure the temperature of another system.
Although the concept of thermodynamic equilibrium is fundamental to thermodynamics and was clearly
stated in the nineteenth century, the desire to label its statement explicitly as a law was not widely felt
until Fowler and Planck stated it in the 1930s, long after the first, second, and third law were already
widely understood and recognized. Hence it was numbered the zeroth law. The importance of the law as

86. a foundation to the earlier laws is that it allows the definition of temperature in a non-circular way
without reference to entropy, its conjugate variable.
First law
The first law of thermodynamics may be stated thus:
Increase in internal energy of a body = heat supplied to the body - work done by the body. U = Q - W
For a thermodynamic cycle, the net heat supplied to the system equals the net work done by the
system.
More specifically, the First Law encompasses several principles:
The law of conservation of energy.
This states that energy can be neither created nor destroyed. However, energy can change forms, and
energy can flow from one place to another. The total energy of an isolated system remains the same.
The concept of internal energy and its relationship to temperature.
If a system, for example a rock, has a definite temperature, then its total energy has three
distinguishable components. If the rock is flying through the air, it has kinetic energy. If it is high above
the ground, it has gravitational potential energy. In addition to these, it has internal energy which is the
sum of the kinetic energy of vibrations of the atoms in the rock, and other sorts of microscopic motion,
and of the potential energy of interactions between the atoms within the rock. Other things being equal,
the internal energy increases as the rock's temperature increases. The concept of internal energy is the
characteristic distinguishing feature of the first law of thermodynamics.
The flow of heat is a form of energy transfer.
In other words, a quantity of heat that flows from a hot body to a cold one can be expressed as an
amount of energy being transferred from the hot body to the cold one.
Performing work is a form of energy transfer.
For example, when a machine lifts a heavy object upwards, some energy is transferred from the
machine to the object. The object acquires its energy in the form of gravitational potential energy in this
example.
Combining these principles leads to one traditional statement of the first law of thermodynamics: it is
not possible to construct a perpetual motion machine which will continuously do work without
consuming energy.
Second law

87. The second law of thermodynamics asserts the existence of a quantity called the entropy of a system
and further states that
When two isolated systems in separate but nearby regions of space, each in thermodynamic equilibrium
in itself (but not necessarily in equilibrium with each other at first) are at some time allowed to interact,
breaking the isolation that separates the two systems, allowing them to exchange matter or energy,
they will eventually reach a mutual thermodynamic equilibrium. The sum of the entropies of the initial,
isolated systems is less than or equal to the entropy of the final combination of exchanging systems. In
the process of reaching a new thermodynamic equilibrium, total entropy has increased, or at least has
not decreased.
It follows that the entropy of an isolated macroscopic system never decreases. The second law states
that spontaneous natural processes increase entropy overall, or in another formulation that heat can
spontaneously be conducted or radiated only from a higher-temperature region to a lower-temperature
region, but not the other way around.
The second law refers to a wide variety of processes, reversible and irreversible. Its main import is to tell
about irreversibility.
The prime example of irreversibility is in the transfer of heat by conduction or radiation. It was known
long before the discovery of the notion of entropy that when two bodies of different temperatures are
connected with each other by purely thermal connection, conductive or radiative, then heat always
flows from the hotter body to the colder one. This fact is part of the basic idea of heat, and is related
also to the so-called zeroth law, though the textbooks' statements of the zeroth law are usually reticent
about that, because they have been influenced by Carathéodory's basing his axiomatics on the law of
conservation of energy and trying to make heat seem a theoretically derivative concept instead of an
axiomatically accepted one. Šilahvý (1997) notes that Carathéodory's approach does not work for the
description of irreversible processes that involve both heat conduction and conversion of kinetic energy
into internal energy by viscosity (which is another prime example of irreversibility), because "the
mechanical power and the rate of heating are not expressible as differential forms in the 'external
parameters'".[10]
The second law tells also about kinds of irreversibility other than heat transfer, and the notion of
entropy is needed to provide that wider scope of the law.
According to the second law of thermodynamics, in a reversible heat transfer, an element of heat
transferred, δQ, is the product of the temperature (T), both of the system and of the sources or
destination of the heat, with the increment (dS) of the system's conjugate variable, its entropy (S)
View formula on Wikipedia[1]
The second law defines entropy, which may be viewed not only as a macroscopic variable of classical
thermodynamics, but may also be viewed as a measure of deficiency of physical information about the
microscopic details of the motion and configuration of the system, given only predictable experimental

88. reproducibility of bulk or macroscopic behavior as specified by macroscopic variables that allow the
distinction to be made between heat and work. More exactly, the law asserts that for two given
macroscopically specified states of a system, there is a quantity called the difference of entropy
between them. The entropy difference tells how much additional microscopic physical information is
needed to specify one of the macroscopically specified states, given the macroscopic specification of the
other, which is often a conveniently chosen reference state. It is often convenient to presuppose the
reference state and not to explicitly state it. A final condition of a natural process always contains
microscopically specifiable effects which are not fully and exactly predictable from the macroscopic
specification of the initial condition of the process. This is why entropy increases in natural processes.
The entropy increase tells how much extra microscopic information is needed to tell the final
macroscopically specified state from the initial macroscopically specified state.[11]
Third law
The third law of thermodynamics is sometimes stated as follows:
The entropy of a perfect crystal at absolute zero is exactly equal to zero.
At zero temperature the system must be in a state with the minimum thermal energy. This statement
holds true if the perfect crystal has only one state with minimum energy. Entropy is related to the
number of possible microstates according to S = kBln(Ω), where S is the entropy of the system, kB
Boltzmann's constant, and Ω the number of microstates (e.g. possible configurations of atoms). At
absolute zero there is only 1 microstate possible (Ω=1) and ln(1) = 0.
A more general form of the third law that applies to systems such as glasses that may have more than
one minimum energy state:
The entropy of a system approaches a constant value as the temperature approaches zero.
The constant value (not necessarily zero) is called the residual entropy of the system.
History
See also: Philosophy of thermal and statistical physics
Count Rumford (born Benjamin Thompson) showed, about 1797, that mechanical action can generate
indefinitely large amounts of heat, so challenging the caloric theory. The historically first established
thermodynamic principle which eventually became the second law of thermodynamics was formulated
by Sadi Carnot during 1824. By 1860, as formalized in the works of those such as Rudolf Clausius and
William Thomson, two established principles of thermodynamics had evolved, the first principle and the
second principle, later restated as thermodynamic laws. By 1873, for example, thermodynamicist Josiah
Willard Gibbs, in his memoir Graphical Methods in the Thermodynamics of Fluids, clearly stated the first
two absolute laws of thermodynamics. Some textbooks throughout the 20th century have numbered
the laws differently. In some fields removed from chemistry, the second law was considered to deal with
the efficiency of heat engines only, whereas what was called the third law dealt with entropy increases.

89. Directly defining zero points for entropy calculations was not considered to be a law. Gradually, this
separation was combined into the second law and the modern third law was widely adopted.
See also
Conservation law
Third law of thermodynamics
Entropy production
Heat death of the universe
Laws of science
Table of thermodynamic equations
Ginsberg's Theorem
References
↑ 1.0 1.1 1.2 Guggenheim, E.A. (1985). Thermodynamics. An Advanced Treatment for Chemists and
Physicists, seventh edition, North Holland, Amsterdam, ISBN 0-444-86951-4.
↑ 2.0 2.1 Kittel, C. Kroemer, H. (1980). Thermal Physics, second edition, W.H. Freeman, San Francisco,
ISBN 0-7167-1088-9.
↑ 3.0 3.1 Adkins, C.J. (1968). Equilibrium Thermodynamics, McGraw-Hill, London, ISBN 0-07-084057-1.
↑ 4.0 4.1 Kondepudi D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-
0-470-01598-8.
↑ 5.0 5.1 Lebon, G., Jou, D., Casas-Vázquez, J. (2008). Understanding Non-equilibrium Thermodynamics.
Foundations, Applications, Frontiers, Springer, Berlin, ISBN 978-3-540-74252-4.
↑ Chris Vuille; Serway, Raymond A.; Faughn, Jerry S. (2009). College physics. Belmont, CA: Brooks/Cole,
Cengage Learning. p. 355. ISBN 0-495-38693-6.
http://books.google.ca/books?id=CX0u0mIOZ44C&pg=PT355.
↑ Balescu, R. (1975). Equilibrium and Nonequilibrium Statistical Mechanics, Wiley, New York, ISBN 0-
471-04600-0.
↑ De Groot, S.R., Mazur, P. (1962). Non-equilibrium Thermodynamics, North Holland, Amsterdam.
↑ Glansdorff, P., Prigogine, I. (1971). Thermodynamic Theory of Structure, Stability and Fluctuations,
Wiley-Interscience, London, ISBN 0-471-30280-5.

90. ↑ Šilhavý, M. (1997). The Mechanics and Thermodynamics of Continuous Media, Springer, Berlin, ISBN
3-540-58378-5, page 137.
↑ Ben-Naim, A. (2008). A Farewell to Entropy: Statistical Thermodynamics Based on Information, World
Scientific, New Jersey, ISBN 978-981-270-706-2.
Further reading
Atkins, Peter, 2007. Four Laws That Drive the Universe. OUP Oxford.
Goldstein, Martin, and Inge F., 1993. The Refrigerator and the Universe. Harvard Univ. Press. A gentle
introduction.ar:‫ال حراري ة ال دي نام ي كا ق وان ين‬
ca:Lleis de la termodinàmica cs:Termodynamický zákon de:Thermodynamik#Kurze Zusammenfassung
der Hauptsätze fa:‫ ت رمودي نام يک ق وان ين‬fr:Principes de la thermodynamique gl:Leis da termodinámica
ko:열역학 법칙 id:Hukum termodinamika lt:Termodinamikos dėsniai
ml: ms:Hukum termodinamik nl:Hoofdwetten van de
thermodynamica ro:Principiile termodinamicii ru:Начала термодинамики sl:Zakoni termodinamike
fi:Termodynamiikan pääsäännöt sv:Termodynamikens huvudsatser th:
tr:Termodinamik kanunları uk:Закони термодинаміки
Retrieved from "http://mediawikifr.dp.teoma.com/wiki/Laws_of_thermodynamics"
Category: Laws of thermodynamics
The content on this page originates from Wikipedia and is licensed under the GNU Free Document
License or the Creative Commons CC-BY-SA license.
Related Web Search
Thermodynamic Laws
Expand Your Search
Entropy
Heat Transfer
Laws of Physics

91. Related Q&A
Q
What is the First Law of Thermodynamics?
The first law of thermodynamics is that energy can be transformed but not destroyed or
created. This is also known as energy conservation. It could be argued that humans are
energy...Read more »
Source:answers.ask.com
Q
What is the Third Law of Thermodynamics?
The third law of thermodynamics basically states that it is impossible to cool an object all the
way down to absolute zero. The theory is based on the entropy of perfect crystals.Read more
»
Source:answers.ask.com
Q
What are the Laws of Thermodynamics?
The laws of thermodynamics describe the movement of heat and work in the thermodynamic
process. They have become some of the most important in all of physics. Look here for more
in...Read more »
Source:answers.ask.com
Related Images

92. More Related Images »NCBI
Skip to main content
Skip to navigation
Resources
All Resources
Chemicals & Bioassays

93. BioSystems
PubChem BioAssay
PubChem Compound
PubChem Structure Search
PubChem Substance
All Chemicals & Bioassays Resources...
DNA & RNA
BLAST (Basic Local Alignment Search Tool)
BLAST (Stand-alone)
E-Utilities
GenBank
GenBank: BankIt
GenBank: Sequin
GenBank: tbl2asn
Genome Workbench
Influenza Virus
Nucleotide Database
PopSet
Primer-BLAST
ProSplign
Reference Sequence (RefSeq)
RefSeqGene
Sequence Read Archive (SRA)
Splign
Trace Archive

94. UniGene
UniSTS
All DNA & RNA Resources...
Data & Software
BLAST (Basic Local Alignment Search Tool)
BLAST (Stand-alone)
Cn3D
Conserved Domain Search Service (CD Search)
E-Utilities
GenBank: BankIt
GenBank: Sequin
GenBank: tbl2asn
Genome ProtMap
Genome Workbench
Primer-BLAST
ProSplign
PubChem Structure Search
SNP Submission Tool
Splign
Vector Alignment Search Tool (VAST)
All Data & Software Resources...
Domains & Structures
BioSystems
Cn3D
Conserved Domain Database (CDD)

95. Conserved Domain Search Service (CD Search)
Structure (Molecular Modeling Database)
Vector Alignment Search Tool (VAST)
All Domains & Structures Resources...
Genes & Expression
BioSystems
Database of Genotypes and Phenotypes (dbGaP)
E-Utilities
Gene
Gene Expression Omnibus (GEO) Database
Gene Expression Omnibus (GEO) Datasets
Gene Expression Omnibus (GEO) Profiles
Genome Workbench
HomoloGene
Map Viewer
Online Mendelian Inheritance in Man (OMIM)
RefSeqGene
UniGene
All Genes & Expression Resources...
Genetics & Medicine
Bookshelf
Database of Genotypes and Phenotypes (dbGaP)
Genetic Testing Registry
Influenza Virus
Map Viewer

96. Online Mendelian Inheritance in Man (OMIM)
PubMed
PubMed Central (PMC)
PubMed Clinical Queries
RefSeqGene
All Genetics & Medicine Resources...
Genomes & Maps
Database of Genomic Structural Variation (dbVar)
GenBank: tbl2asn
Genome
Genome Project
Genome ProtMap
Genome Workbench
Influenza Virus
Map Viewer
Nucleotide Database
PopSet
ProSplign
Sequence Read Archive (SRA)
Splign
Trace Archive
UniSTS
All Genomes & Maps Resources...
Homology
BLAST (Basic Local Alignment Search Tool)

97. BLAST (Stand-alone)
BLAST Link (BLink)
Conserved Domain Database (CDD)
Conserved Domain Search Service (CD Search)
Genome ProtMap
HomoloGene
Protein Clusters
All Homology Resources...
Literature
Bookshelf
E-Utilities
Journals in NCBI Databases
MeSH Database
NCBI Handbook
NCBI Help Manual
NCBI News
PubMed
PubMed Central (PMC)
PubMed Clinical Queries
PubMed Health
All Literature Resources...
Proteins
BioSystems
BLAST (Basic Local Alignment Search Tool)
BLAST (Stand-alone)

98. BLAST Link (BLink)
Conserved Domain Database (CDD)
Conserved Domain Search Service (CD Search)
E-Utilities
ProSplign
Protein Clusters
Protein Database
Reference Sequence (RefSeq)
All Proteins Resources...
Sequence Analysis
BLAST (Basic Local Alignment Search Tool)
BLAST (Stand-alone)
BLAST Link (BLink)
Conserved Domain Search Service (CD Search)
Genome ProtMap
Genome Workbench
Influenza Virus
Primer-BLAST
ProSplign
Splign
All Sequence Analysis Resources...
Taxonomy
Taxonomy
Taxonomy Browser
Taxonomy Common Tree

99. All Taxonomy Resources...
Training & Tutorials
NCBI Education Page
NCBI Handbook
NCBI Help Manual
NCBI News
Science Primer
All Training & Tutorials Resources...
Variation
Database of Genomic Structural Variation (dbVar)
Database of Genotypes and Phenotypes (dbGaP)
Database of Single Nucleotide Polymorphisms (dbSNP)
SNP Submission Tool
All Variation Resources...
How To
All How To
Chemicals & Bioassays
DNA & RNA
Data & Software
Domains & Structures
Genes & Expression
Genetics & Medicine
Genomes & Maps
Homology
Literature

100. Proteins
Sequence Analysis
Taxonomy
Training & Tutorials
Variation
About NCBI Accesskeys
My NCBISign in to NCBISign Out
PMC
US National Library of Medicine
National Institutes of Health
Top of Form
Search term Search database
PMC
Search
Limits
Advanced
Journal list
Help
Bottom of Form
Journal List >
Appl Microbiol >
v.11(6); Nov 1963 >

101. PMC1058043
Appl Microbiol. 1963 November; 11(6): 523–528.
PMCID: PMC1058043
Microbiological Production of Gibberellic Acid in Glucose Media1
A. Sanchez-Marroquin
Escuela Nacional de Ciencias Quimícas, Universidad de México, Mexico, D.F., Mexico
1This paper was presented at the II Latin-American Congress of Microbiology, San José, Costa Rica, 10-
16 December 1961.
Author information ► Copyright and License information ►
Copyright notice
Abstract
Gibberellic acid production from various substrates was studied in 43 strains of Fusarium, among which
F. moniliforme strain IOC-3326 was selected as the best producer. Experiments were carried out in
shaker flasks and pilot plant fermentors. The results indicate that the best substrate for gibberellic acid
production with this strain is composed of the following: glucose, 20 g; corn steep liquor, 25 g;
ammonium nitrate, 2.6 g; monopotassium phosphate, 0.5 g; potassium sulfate, 0.2 g; and water, 1000
ml. Glucose, ammonium nitrate, and corn steep liquor were found to be critical. With this medium,
maximal yields of 1196 mg per liter in shaker flasks and 997 mg per liter in fermentors were produced.
Full text
Full text is available as a scanned copy of the original print version. Get a printable copy (PDF file) of the
complete article (923K), or click on a page image below to browse page by page. Links to PubMed are
also available for Selected References.

103. 523

105. 524

107. 525

109. 526

111. 527

113. 528
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
Bird HL, Pugh CT. A Paper Chromatographic Separation of Gibberellic Acid and Gibberellin A. Plant
Physiol. 1958 Jan;33(1):45–46. [PMC free article] [PubMed]
DARKEN MA, JENSEN AL, SHU P. Production of gibberellic acid by fermentation. Appl Microbiol. 1959
Sep;7:301–303. [PMC free article] [PubMed]
STODOLA FH, RAPER KB, FENNELL DI, CONWAY HF, SOHNS VE, LANGFORD CT, JACKSON RW. The
microbiological production of gibberellins A and X. Arch Biochem Biophys. 1955 Jan;54(1):240–245.
[PubMed]
Articles from Applied Microbiology are provided here courtesy of American Society for Microbiology
(ASM)
Formats:
Summary
|
Page Browse
|
PDF (923K)
Related citations in PubMed
Gibberellic acid production by Fusarium moniliforme on lupin seed extract. [Acta Microbiol Pol. 1994]
Gibberellic acid production by Fusarium moniliforme on lupin seed extract.
Gulewicz K, Rataj-Guranowska M, Lukaszewska N, Michalski Z. Acta Microbiol Pol. 1994; 43(1):73-7.
Survey of some Fusarium moniliforme strains from different host plants for compounds possessing
gibberellin-like activity. [Zentralbl Bakteriol Parasitenkd Infektionsk...]

114. Survey of some Fusarium moniliforme strains from different host plants for compounds possessing
gibberellin-like activity.
El-Bahrawi S. Zentralbl Bakteriol Parasitenkd Infektionskr Hyg. 1977; 132(2):178-83.
Biosynthesis of gibberellic acid from milk permeate in repeated batch operation by a mutant Fusarium
moniliforme cells immobilized on loofa sponge. [Bioresour Technol. 2009]
Biosynthesis of gibberellic acid from milk permeate in repeated batch operation by a mutant Fusarium
moniliforme cells immobilized on loofa sponge.
Meleigy SA, Khalaf MA. Bioresour Technol. 2009 Jan; 100(1):374-9. Epub 2008 Aug 5.
Morphological mutants of Gibberella fujikuroi for enhanced production of gibberellic acid. [J Appl
Microbiol. 2006]
Morphological mutants of Gibberella fujikuroi for enhanced production of gibberellic acid.
Lale G, Jogdand VV, Gadre RV. J Appl Microbiol. 2006; 100(1):65-72.
EFFECTS OF CORN STEEP LIQUOR AND THIAMINE ON L-GLUTAMIC ACID FERMENTATION OF
HYDROCARBONS.IV. UTILIZATION OF HYDROCARBONS BY MICROORGANISMS. [Appl Microbiol. 1965]
EFFECTS OF CORN STEEP LIQUOR AND THIAMINE ON L-GLUTAMIC ACID FERMENTATION OF
HYDROCARBONS.IV. UTILIZATION OF HYDROCARBONS BY MICROORGANISMS.
TAKAHASHI J, KOBAYASHI K, IMADA Y, YAMADA K. Appl Microbiol. 1965 Jan; 13:1-4.
See reviews... See all...
Links
PubMed
PubMed
PubMed citation for this article
Substance
Substance
PubChem Substance links
Taxonomy
Taxonomy
Related taxonomy entry

115. Taxonomy Tree
Taxonomy Tree
Recent activity
Clear Turn Off Turn On
Microbiological Production of Gibberellic Acid in Glucose Media
Microbiological Production of Gibberellic Acid in Glucose Media
Applied Microbiology. 1963 Nov; 11(6)523-528
PMC
Your browsing activity is empty.
Activity recording is turned off.
Turn recording back on
See more...
You are here: NCBI > Literature > PubMed Central (PMC)
Write to the Help Desk
Simple NCBI Directory
Getting Started
NCBI Education
NCBI Help Manual
NCBI Handbook
Training & Tutorials
Resources
Chemicals & Bioassays
Data & Software
DNA & RNA

116. Domains & Structures
Genes & Expression
Genetics & Medicine
Genomes & Maps
Homology
Literature
Proteins
Sequence Analysis
Taxonomy
Training & Tutorials
Variation
Popular
PubMed
Nucleotide
BLAST
PubMed Central
Gene
Bookshelf
Protein
OMIM
Genome
SNP
Structure
Featured
Genetic Testing Registry

117. PubMed Health
GenBank
Reference Sequences
Map Viewer
Human Genome
Mouse Genome
Influenza Virus
Primer-BLAST
Sequence Read Archive
NCBI Information
About NCBI
Research at NCBI
NCBI Newsletter
NCBI FTP Site
NCBI on Facebook
NCBI on Twitter
NCBI on YouTube
External link. Please review our privacy policy.
NLM
NIH
DHHS
USA.gov
Copyright | Disclaimer | Privacy | Accessibility | Contact
National Center for Biotechnology Information, U.S. National Library of Medicine 8600 Rockville Pike,
Bethesda MD, 20894 USA
External link. Please review our privacy policy.

118. f42da7e2-09e3-4200-8fda-9d0df24fc5ad
Y2:f42da7e2-09e3-4200-8fda-9d0df24fc5adSkip to content
Librarians
Authors & Editors
Societies
Register
Sign in
Mobile
Browse
Products
Redeem a voucher
Shortlist
Cart
The online platform for Taylor & Francis Group content
Search
Search
Advanced Search Within current journal Entire site
Home > List of Issues > Table of Contents > Evaluation of Some Food Industry Wastes for Production of
Gibberellic Acid by Fungal Source
Browse journal
View all volumes and issues
Current issue

119. Latest articles
Most read articles
Most cited articles
Authors and submissions
Call for papers
Instructions for authors
Submit online
Subscribe
Journal information
About this journal
Aims & scope
Editorial board
Abstracting & indexing
Related websites
News & offers
Environmental Technology
Volume 18, Issue 5, 1997

120. Evaluation of Some Food Industry Wastes for Production of Gibberellic Acid by Fungal Source
Preview
Access options
DOI:
10.1080/09593331808616569
N. Cihangir & N. Aksöza
pages 533-537
Publishing models and article dates explained
Version of record first published: 11 May 2010
Article Views: 13
Alert me
TOC email alert
TOC RSS feed
Citation email alert
Citation RSS feed
Abstract
The control of environmental pollution and the recovery of agricultural, industrial and municipal
wastes by converting them into useful products are two relevant biotechnological goals. In this
study, the possibility of utilising food industry waste and residues as sources of carbon for
gibberellic acid production by Aspergillus niger was investigated. Media prepared from
molasses, vinasse, whey, sugar-beet waste and fruit pomace were used and GA3 yields were
found in concentrations 155, 136.57, 120, 73, 118.13 mg l−1 respectively in such media. It was
observed that food industry wastes can be used and evaluated as cheap sources of carbon for
gibberellic acid production.
Download full text
Keywords
food industry wastes,
evaluation,
production,

121. gibberellic acid
Related
Add to shortlist
Link
Permalink
http://dx.doi.org/10.1080/09593331808616569
Download Citation
Recommend to:
A friend
First page preview
Close
Download full text
Click to increase image sizeClick to decrease image size
Information
Citations
Reprints & permissions
Details
Citation information: Web of Science ®
Version of record first published: 11 May 2010
Journal news
2011 Impact Factor: 1.406 ©2012 Thomson Reuters, 2011 Journal Citation Report®
New journal - Environmental Technology Reviews for 2012!

122. Librarians
Librarians' area
Pricing
Institutional account
Access entitlements
Co-branding
IP ranges
Link resolver preferences
Usage reports
Authors & Editors
Book authors
Journal authors
Reference work authors
Editors
Societies
Current partners
Publish with us
Help & Information

123. Help
FAQs
Contact us
Feedback form
Press releases
Taylor & Francis Group
Privacy Policy & Cookies
Terms & Conditions
Accessibility
Feedback
Powered by Atypon® Literatum
© 2013 Informa plc
Skip to content
Librarians
Authors & Editors
Societies
Register
Sign in
Mobile
Browse

124. Products
Redeem a voucher
Shortlist
Cart
The online platform for Taylor & Francis Group content
Search
Search
Advanced Search Within current journal Entire site
Home > List of Issues > Table of Contents > Evaluation of Some Food Industry Wastes for Production of
Gibberellic Acid by Fungal Source
Browse journal
View all volumes and issues
Current issue
Latest articles
Most read articles
Most cited articles
Authors and submissions
Call for papers
Instructions for authors
Submit online
Subscribe
Journal information
About this journal

125. Aims & scope
Editorial board
Abstracting & indexing
Related websites
News & offers
Environmental Technology
Volume 18, Issue 5, 1997
Evaluation of Some Food Industry Wastes for Production of Gibberellic Acid by Fungal Source
Preview
Access options
DOI:
10.1080/09593331808616569
N. Cihangir & N. Aksöza
pages 533-537
Publishing models and article dates explained
Version of record first published: 11 May 2010
Article Views: 13

126. Alert me
TOC email alert
TOC RSS feed
Citation email alert
Citation RSS feed
Abstract
The control of environmental pollution and the recovery of agricultural, industrial and municipal
wastes by converting them into useful products are two relevant biotechnological goals. In this
study, the possibility of utilising food industry waste and residues as sources of carbon for
gibberellic acid production by Aspergillus niger was investigated. Media prepared from
molasses, vinasse, whey, sugar-beet waste and fruit pomace were used and GA3 yields were
found in concentrations 155, 136.57, 120, 73, 118.13 mg l−1 respectively in such media. It was
observed that food industry wastes can be used and evaluated as cheap sources of carbon for
gibberellic acid production.
Download full text
Keywords
food industry wastes,
evaluation,
production,
gibberellic acid
Related
Add to shortlist
Link
Permalink
http://dx.doi.org/10.1080/09593331808616569
Download Citation
Recommend to:
A friend
First page preview
Close
Download full text

127. Click to increase image sizeClick to decrease image size
Information
Citations
Reprints & permissions
Details
Citation information: Web of Science ®
Version of record first published: 11 May 2010
Journal news
2011 Impact Factor: 1.406 ©2012 Thomson Reuters, 2011 Journal Citation Report®
New journal - Environmental Technology Reviews for 2012!
Librarians
Librarians' area
Pricing

128. Institutional account
Access entitlements
Co-branding
IP ranges
Link resolver preferences
Usage reports
Authors & Editors
Book authors
Journal authors
Reference work authors
Editors
Societies
Current partners
Publish with us
Help & Information
Help
FAQs
Contact us
Feedback form
Press releases
Taylor & Francis Group
Privacy Policy & Cookies
Terms & Conditions
Accessibility
Feedback
Powered by Atypon® Literatum
© 2013 Informa plc

129. Skip to content
Librarians
Authors & Editors
Societies
Register
Sign in
Mobile
Browse
Products
Redeem a voucher
Shortlist
Cart
The online platform for Taylor & Francis Group content
Search
Search
Advanced Search Within current journal Entire site
Home > List of Issues > Table of Contents > Evaluation of Some Food Industry Wastes for Production of
Gibberellic Acid by Fungal Source
Browse journal
View all volumes and issues
Current issue
Latest articles
Most read articles

130. Most cited articles
Authors and submissions
Call for papers
Instructions for authors
Submit online
Subscribe
Journal information
About this journal
Aims & scope
Editorial board
Abstracting & indexing
Related websites
News & offers
Environmental Technology
Volume 18, Issue 5, 1997
Evaluation of Some Food Industry Wastes for Production of Gibberellic Acid by Fungal Source
Preview
Access options

131. DOI:
10.1080/09593331808616569
N. Cihangir & N. Aksöza
pages 533-537
Publishing models and article dates explained
Version of record first published: 11 May 2010
Article Views: 13
Alert me
TOC email alert
TOC RSS feed
Citation email alert
Citation RSS feed
Abstract
The control of environmental pollution and the recovery of agricultural, industrial and municipal
wastes by converting them into useful products are two relevant biotechnological goals. In this
study, the possibility of utilising food industry waste and residues as sources of carbon for
gibberellic acid production by Aspergillus niger was investigated. Media prepared from
molasses, vinasse, whey, sugar-beet waste and fruit pomace were used and GA3 yields were
found in concentrations 155, 136.57, 120, 73, 118.13 mg l−1 respectively in such media. It was
observed that food industry wastes can be used and evaluated as cheap sources of carbon for
gibberellic acid production.
Download full text
Keywords
food industry wastes,
evaluation,
production,
gibberellic acid
Related
Add to shortlist

132. Link
Permalink
http://dx.doi.org/10.1080/09593331808616569
Download Citation
Recommend to:
A friend
First page preview
Close
Download full text
Click to increase image sizeClick to decrease image size
Information
Citations
Reprints & permissions
Details
Citation information: Web of Science ®
Version of record first published: 11 May 2010
Journal news
2011 Impact Factor: 1.406 ©2012 Thomson Reuters, 2011 Journal Citation Report®
New journal - Environmental Technology Reviews for 2012!

133. Librarians
Librarians' area
Pricing
Institutional account
Access entitlements
Co-branding
IP ranges
Link resolver preferences
Usage reports
Authors & Editors
Book authors
Journal authors
Reference work authors
Editors
Societies
Current partners
Publish with us
Help & Information

134. Help
FAQs
Contact us
Feedback form
Press releases
Taylor & Francis Group
Privacy Policy & Cookies
Terms & Conditions
Accessibility
Feedback
Powered by Atypon® Literatum
Gibberellic acid
From Wikipedia, the free encyclopedia
Jump to: navigation, search
This article needs additional citations for verification. Please help improve this article by
adding citations to reliable sources. Unsourced material may be challenged and removed.
(November 2012)
Gibberellic acid

135. IUPAC name[show]
Identifiers
CAS number 77-06-5
PubChem 522636
ChemSpider 7995349
UNII BU0A7MWB6L
EC number 201-001-0
KEGG C01699
ChEBI CHEBI:28833
ChEMBL CHEMBL566653
Jmol-3D images Image 1
SMILES
[show]
InChI
[show]
Properties
Molecular formula C19H22O6

136. Molar mass 346.37 g/mol
Melting point 233 - 235 °C (decomposition)
Solubility in water 5 g/l (20 °C)
Hazards
EU classification Irritant (Xi)
R-phrases R36
S-phrases R26, S36
(verify) (what is: / ?)
Except where noted otherwise, data are given for materials
in their standard state (at 25 °C, 100 kPa)
Infobox references
Gibberellic acid (also called Gibberellin A3, GA, and GA3) is a hormone found in plants. Its
chemical formula is C19H22O6. When purified, it is a white to pale-yellow solid.
Gibberellic acid is a simple gibberellin, a pentacyclic diterpene acid promoting growth and
elongation of cells. It affects decomposition of plants and helps plants grow if used in small
amounts, but eventually plants develop tolerance to it[citation needed]. GA stimulates the cells of
germinating seeds to produce mRNA molecules that code for hydrolytic enzymes. Gibberellic
acid is a very potent hormone whose natural occurrence in plants controls their development.
Since GA regulates growth, applications of very low concentrations can have a profound effect
while too much will have the opposite effect.[1] It is usually used in concentrations between 0.01
and 10 mg/L.
GA was first identified in Japan in 1935, as a metabolic byproduct of the plant pathogen
Gibberella fujikuroi (thus the name), which afflicts rice plants; fujikuroi-infected plants develop
bakanae ("foolish seedling"), which causes them to grow so much taller than normal that they
die from no longer being sturdy enough to support their own weight.
Gibberellins have a number of effects on plant development. They can stimulate rapid stem and
root growth, induce mitotic division in the leaves of some plants, and increase seed germination
rate.

137. Gibberellic acid is sometimes used in laboratory and greenhouse settings to trigger germination
in seeds that would otherwise remain dormant.[1] It is also widely used in the grape-growing
industry as a hormone to induce the production of larger bundles and bigger grapes, especially
Thompson seedless grapes. In the Okanagan and Creston valleys, it is also used as a growth
replicator in the cherry industry.
[edit] See also
Gibberellin
Plant hormone
6-Benzylaminopurine
[edit] References
1. ^ a b Riley, John M.. "Gibberellic Acid for Fruit Set and Seed Germination".
http://www.crfg.org/tidbits/gibberellic.html. Retrieved 26 Oct 2012.
[edit] External links
No longer maintained. Safety MSDS data
Synonyms at webbook.nist.gov
www.crfg.org
Retrieved from "http://en.wikipedia.org/w/index.php?title=Gibberellic_acid&oldid=535424207"
View page ratings
Rate this page
What's this?
Trustworthy
Objective
Complete
Well-written
I am highly knowledgeable about this topic (optional)

138. Submit ratings
Saved successfully
Your ratings have not been submitted yet
Categories:
Plant hormones
Hidden categories:
Articles needing additional references from November 2012
All articles needing additional references
Articles with changed EBI identifier
Chemboxes which contain changes to verified fields
All articles with unsourced statements
Articles with unsourced statements from October 2012
Navigation menu
Personal tools
Create account
Log in
Namespaces
Article
Talk
Variants
Views
Read
Edit
View history
Actions
Search
Search
Navigation

139. Main page
Contents
Featured content
Current events
Random article
Donate to Wikipedia
Interaction
Help
About Wikipedia
Community portal
Recent changes
Contact Wikipedia
Toolbox
What links here
Related changes
Upload file
Special pages
Permanent link
Page information
Cite this page
Rate this page
Print/export
Create a book
Download as PDF
Printable version
Languages
Català
Deutsch
Español
‫ف ار سی‬
Français
Italiano
Magyar
Nederlands
日本語
Polski
Suomi
Svenska

140. Tiếng Việt
This page was last modified on 28 January 2013 at 23:34.
Text is available under the Creative Commons Attribution-ShareAlike License; additional terms
may apply. See Terms of Use for details.
Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit
organization.
Contact us
Privacy policy
About Wikipedia
Disclaimers
Mobile view
© 2013 Informa plc