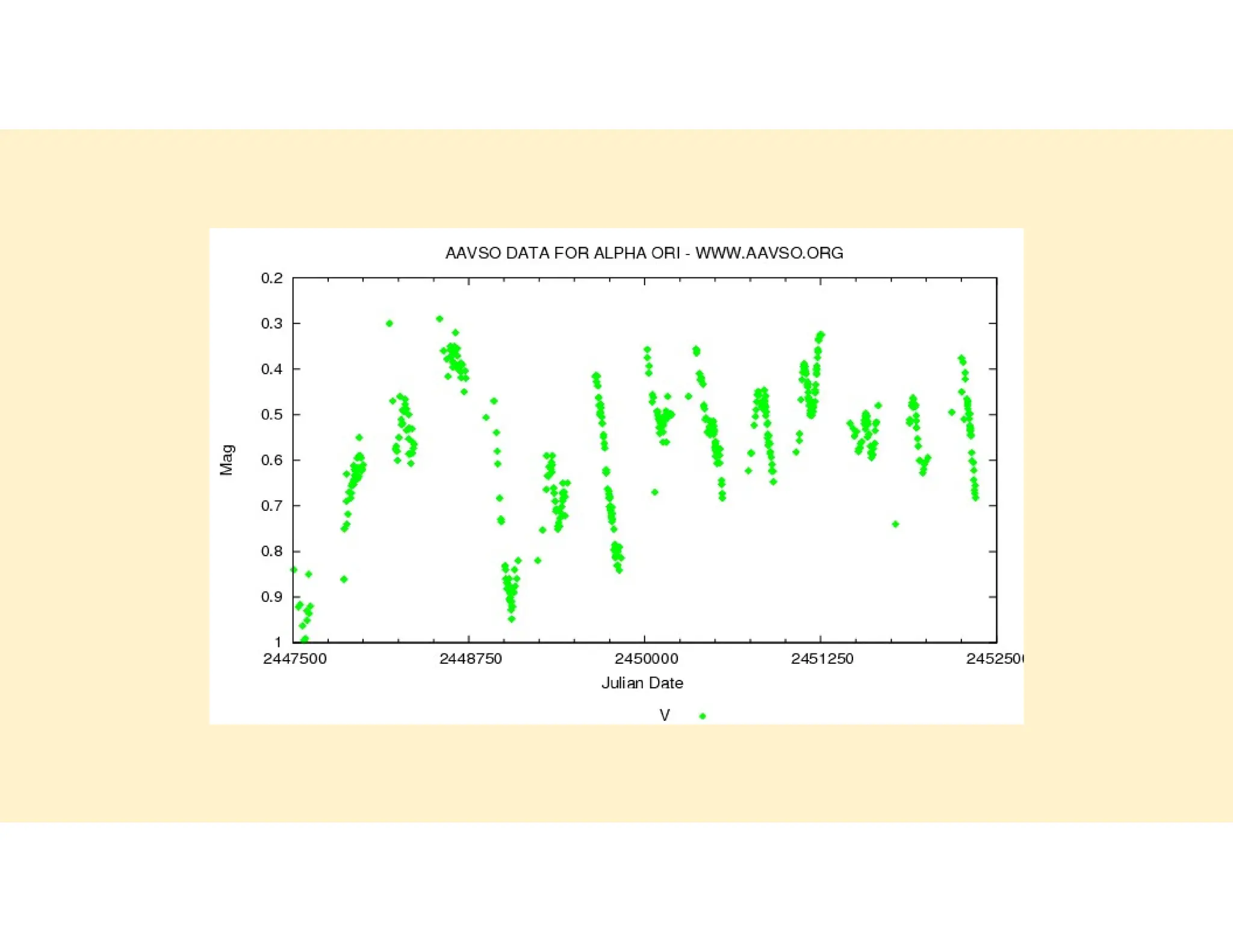
The Julian day system, invented by Joseph Scaliger in 1583, provides a straightforward way to compute the integer difference between calendar dates, beginning with a fixed epoch on January 1, 4713 BC. John F. Herschel later adapted this system for astronomical purposes, establishing a starting point for each Julian day at noon, which helps eliminate calendar ambiguities and facilitates precise timekeeping in astronomy. The document also outlines the calculation methods for determining Julian dates from given Gregorian and Julian calendar dates.

1. Julian
Day

2. Julian Day
It was invented by Joseph Scaliger in
1583. The purpose of the system is to make
it easy to compute an integer (whole
number) difference between one calendar
date and another calendar date.
It is sometimes necessary to express
an instant of observation as so many days
and a fraction of a day after a given
fundamental epoch (1 January 4713 BC), that
is midday as measured on the Greenwich
meridian on 1 January of that year.

3. Julian Day
In Scaliger's time, there were no known historical events before
4713 BC, so his calendar would avoid BC/AD or negative dates.
He also chose the starting point for a Julian period to be the year
when three cycles converge:
1) The solar cycle – 28 YEARS
2) The Metonic cycle – 19 YEARS
3) The indiction cycle – 15 YEARS

4. Julian Day
In 1849, the astronomer John F. Herschel turned Scaliger's
calendar into the astronomical Julian Date system, taking January
1, 4713 BC as JD=0, and counting day numbers from that date. He
also made the starting point of the day at noon, to avoid having
the date change in the middle of the night during the observing
run at least for observers close enough to the Greenwich
Meridian, since JD is usually measured in Universal Time.

6. Julian Day
Key reasons why Julian Date is important in astronomy:
1. Eliminates Calendar Ambiguities
2. Facilitates Precise Timekeeping
3. Provides a Universal Reference for Observations
4. Simplifies Long-Term Calculations
5. Essential for Ephemeris Calculations

7. Julian Day
The number of days that have elapsed since that time is
referred to as the Julian day number, or Julian date*. It is important
to note that each new Julian day begins at 12h 00m UT, half a day
out of step with the civil day in time zone 0.
*Sometimes the modified Julian date, MJD, is quoted. This is
equal to the Julian date minus 2400000.5; MJD zero therefore
begins at 0h on 17 November 1858.

8. Calculation of the JD
Y – year M – month number D – day of the month
• If M > 2, leave Y and M unchanged
Y – 1
If M = 1 or 2, replace Y by and M by M + 12
• In the Gregorian calendar, calculate
A = INT
Y
100
B = 2 –A + INT A
4
In the Julian Calendar, take B = 0
• The required Julian Date is then
JD = INT (365.25(Y + 4716)) + INT (30.6001(M + 1)) + D + B – 1524.5

9. Notes:
*The Julian calendar day Thursday, 4 October 1582 was
followed by the first day of the Gregorian calendar, Friday,
15 October 1582 (the cycle of weekdays was not affected).
*Convert to days if values for hours, minutes, and
seconds are given.
*Systems:
12-hour: AM/PM 24-hour
HH:MM:SS

10. Sample Problem 1 – Calculate the JD corresponding to 1957 October 4.81, the
time of launch of Sputnik 1
Y = 1957 , M = 10, D = 4.81
Because M > 2, Y and M are unchanged
The date is in the Gregorian calendar, so we calculate
A = INT(Y/100) = INT(1957/100) = INT(19.57) = 19
- 13
– 19 + 4 =
= 2 – 19 + INT(19/4) = 2
B = 2 – A + INT (A/4)
JD = INT (365.25(Y + 4716)) + INT (30.6001(M + 1)) + D + B – 1524.5
JD = INT (365.25(1957 + 4716)) + INT (30.6001(10 + 1)) + 4.81 – 13 – 1524.5
JD = INT (365.25(6673)) + INT (30.6001(11)) + 4.81 – 13 – 1524.5
JD = 2437313 + 336 + 4.81 – 13 – 1524.5
JD = 2436116.31

11. Sample Problem 2 – Calculate the JD corresponding to January 27.5, 333
Because M = 1, Y = 333 - 1 = 332 and M = 1 + 12 = 13
The date is in the Julian calendar, so B = 0
JD = INT (365.25(Y + 4716)) + INT (30.6001(M + 1)) + D + B – 1524.5
JD = INT (365.25(332 + 4716)) + INT (30.6001(13 + 1)) + 27.5 + 0 – 1524.5
JD = INT (365.25(5048)) + INT (30.6001(14)) + 27.5 – 1524.5
JD = 1843782 + 428 + 27.5 – 1524.5
JD = 1842713

12. Practice Problem 1
Calculate the JD corresponding to February 29, 2024
(08:10:10 AM) M = 14 Y = 2023 D = 29.340
A = 20 B = 2 – 20 + 5 = -13
JD = INT (365.25(Y + 4716)) + INT (30.6001(M + 1)) + D + B – 1524.5
JD = INT (365.25(2023 + 4716)) + INT (30.6001(14 + 1)) + D + B – 1524.5
JD = INT (365.25(6739)) + INT (30.6001(15)) + D + B – 1524.5
JD = 2461419 + 459 + 29.340 + -13 – 1524.5
JD = 2460369.84

13. Practice Problem 2
Calculate the JD corresponding to November 14, 1400
1:59:31 PM Y = 1400 M = 11
D = 14.583
JD = INT (365.25(Y + 4716)) + INT (30.6001(M + 1)) + D + B – 1524.5
JD = INT (365.25(1400 + 4716)) + INT (30.6001(11 + 1)) + 14.583 + 0 – 1524.5
JD = INT (365.25(6116)) + INT (30.6001(12)) + 14.583 + 0 – 1524.5
JD = 2233869 + 367 + 14.583 + 0 – 1524.5
JD = 2232726.083