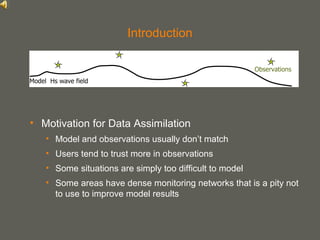
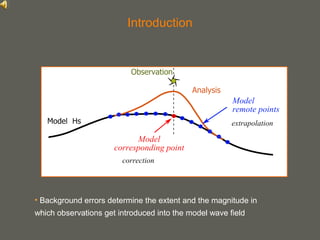
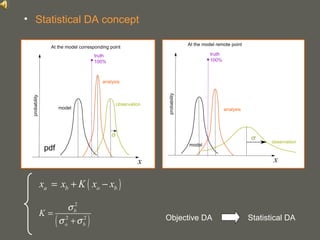
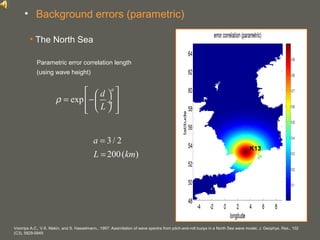
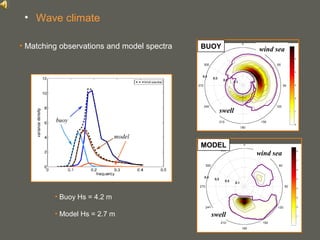
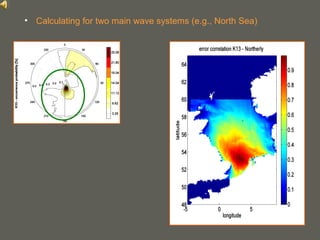
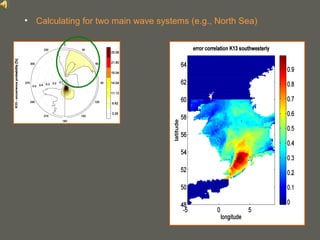
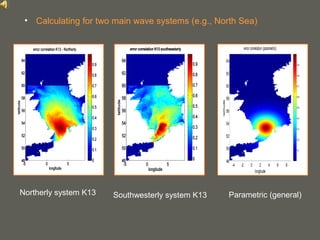
This document proposes a method for calculating the background error covariance matrix (BECM) for wave data assimilation systems. The method considers the local spectral wave climate and the spectral correction model applied. It calculates separate BECMs for different wave systems, such as the northerly and southwesterly systems in the North Sea, without assumptions about wind-sea or swell conditions. The developed method allows objectively computing BECMs based on statistics and implicitly defines the spatial domains where isotropy and homogeneity are fulfilled.