- THE WHAT: The speaker will discuss "bunched black swans", which are long range correlated, wild events. Specifically, the speaker will discuss "bursts" where the time series exceeds a threshold. - THE WHY: Scientists studying climate, space weather, and finance care about bursts. The speaker will provide examples of why this is relevant to the British Antarctic Survey (BAS) and beyond. - THE HOW: The speaker will discuss how they have modeled one class of "routinely extreme" burst problems using an approach building on Mandelbrot's work, involving fractional stable models.

1. Bunched black swans at the
British Antarctic Survey ...
Nick Watkins: NickWatkins@mykolab.com
NERC British Antarctic Survey, Cambridge, UK
Visiting Fellow, Centre for the Analysis of Time Series, LSE
Associate Fellow, Department of Physics, University of Warwick
http://www.mendeley.com/profiles/nicholas-watkins1/
IMA Annual Conference: Mathematics of Planet Earth,
14th March 2013

2. Addendum
• My last talk as a BAS employee, this was an invited presentation at the Institute
of Mathematics and its Applications Annual Conference in London, on 14th March
(Pi Day) 2013.
The meeting’s theme was Mathematics for Planet Earth, and details
of the programme are at http://www.ima.org.uk/viewitem.cfm-cit_id=384212.html
Apart from changing the email address to one which is still in use, I have not
changed or corrected slides.
NWW
30/7/14

3. Summary
• THE WHAT: Will talk about long range correlated, wild, events (colloquially, in my
title, following Taleb, I have called them “bunched black swans”). Will discuss a
particular type of wild event, the “burst” above a threshold.
• THE WHY: Will intersperse examples of why scientists looking at earth’s
climate, space weather (and finance) care about bursts. BAS and beyond …
• THE HOW: Will talk a bit about how my colleagues & I have been modelling one
class of “routinely extreme” burst problem using an approach that builds on
Mandelbrot’s pioneering work in the 60s, and the more recent
fractional stable models (e.g. Samorodnitsky & Taqqu).
• MORE DETAIL: Short review in Watkins, GRL Frontiers, 2013, doi:
10.1002/grl.50103, intended to act as a portal setting Mandelbrot’s work
in context in the large and growing literature in this area.

4. Why BAS ?
Auroral physics
Two examples of many
Foraging

5. The sun and space weather
Solar wind
Magnetosphere
Example of diagnostic is magnetometers,
sensing ionospheric currents. Ultimate
energy source turbulent solar wind.
Ionosphere

6. Fat tails & the sun
Riley, 2012
“Fat” tailed distribution of
velocity of coronal mass
ejections. Lognormal ?
Truncated power law ?
How “fat” is “fat” ?
= How likely is next severe
“Carrington event” ?

7. Persistence & heat waves
• Rather than coming from a fat-tailed
distribution of amplitudes, the severity of an
event might be a result of a long duration.
• Runs of hot days above a fixed threshold, e.g.
summer 1976 in UK, or summer 2003 in
France.
• Direct link to weather
derivatives [e.g. book
by Steve Jewson et al]

8. Finance: persistence & fat tails ?
“ “We were seeing things that were 25-standard deviation
moves, several days in a row,” said David Viniar,
Goldman’s CFO ... [describing catastrophic losses on their
flagship Global Alpha hedge fund]. “What we have to look
at more closely is the phenomenon of the crowded trade
overwhelming market
fundamentals”,
he said. “It makes
you reassess how
big the extreme
moves can be””.
--- FT, August 13th, 2007

9. Several ways to conceptualise “wild”
events
30 July 2014 9
“ Is it a bird, an extreme event, or a cliche ... ?”
– The Economist, March 2011
Colloquial, but resonant
with much experience
Rigorous, but limitations.
Inspired by what we
see in many time series,
and by models of
intermittency

10. Black Swans
30 July 2014 10
• “Rarity …
• … extreme impact …
•… and retrospective
(though not prospective)
predictability”

11. Extremes
30 July 2014 11
1 2 3{ , , , }max Nx x x x

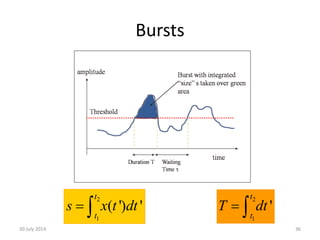
12. Bursts
30 July 2014 12
2
1
[ ( ') ] '
t
t
s x t L dt  2
1
'
t
t
T dt 
Inspired by sandpiles
and SOC.
Compared, for
example to EVT,
does not assume
threshold is in some
sense high.
Can be measured on
time series, or fields,
has links to research on
sojourns, level sets,
etc.

13. Also several ways to conceptualise
clustering of severe events
30 July 2014 13
Bunched Black
Swans

14. Several ways to think about
dependent“wild” events
• If considering extreme values, the largest (or
smallest) of a set, and can use, or infer, a model, then
EV theory [e.g. Gumbel; Coles] is mature … & is now
developed to encompass clustering.
• Rather than EVT, however, today concerned with
burst framework (“grouped grey swans”) .
• Why is burst a different concept, and what kind of
“routinely extreme” randomness does it represent ?
• And why do I use the phrase “routinely extreme”
30 July 2014 14

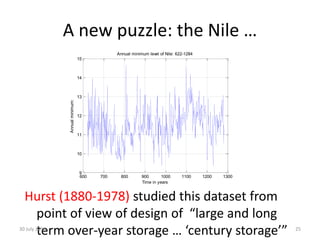
15. Grey swans: “routinely extreme”
• In The Black Swan, Taleb observes that “Extremistan does not
always imply Black Swans. Some events can [be]... somewhat
predictable [ ...]. They are near–Black Swans ... I call this
special case of “gray” swans Mandelbrotian randomness”.
30 July 2014 15
600 700 800 900 1000 1100 1200 1300
9
10
11
12
13
14
15
Annual minimum level of Nile: 622-1284
Annualminimum:
Time in years
As John Prescott put it (and was widely mocked) :
“Extreme events will be the norm”

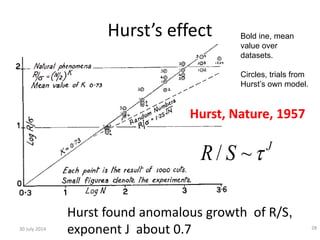
16. Grey swans: “routinely extreme”
• In The Black Swan, Taleb observes that “Extremistan does not
always imply Black Swans. Some events can [be]... somewhat
predictable [ ...]. They are near–Black Swans ... I call this
special case of “gray” swans Mandelbrotian randomness”.
30 July 2014 16
600 700 800 900 1000 1100 1200 1300
9
10
11
12
13
14
15
Annual minimum level of Nile: 622-1284
Annualminimum:
Time in years
Or as JP might have put it:
“Extremely large &/or long-lived
events will be commonplace”

17. Gaussian (normal): “mild” variation
30 July 2014 17
21
exp{ (1/ 2)[( ) / ]) }
2
(p   
 
 
If we want to model
positive rvs an exponential
gives light tails, for example.

18. 30 July 2014
18
Light tail
Heavy tail
Tails may be not just fat however,
but (rigorously) heavy …
Pareto distribution is one such
( ) ( )
x
F x p d   df
( ) 1 ( ) 0,F x F x x   Tail of
df
0
( ) ,
1
( ) 0I
x
F y dx xF y

 
Integrated tail of df
Example, tail of Pareto distribution makes the integral
in the Cramer-Lundberg condition diverge:
0 0
( ) (1 )x x
e x dxF e x dx  
 

   Essential distinction of small & large
claim distributions [Embrechts et al book]

19. … can arise from large jumps
30 July 2014 19

20. Mandelbrot, J. Business, 1963
30 July 2014 20
100 200 300 400 500 600 700 800 900 1000
-5
0
5
10
15
20
25
30
35
40
amplitude
time
stable
Gaussian

21. Mandelbrot: “wild” symptoms …
30 July 2014 21
Heavier than
Normal tails
Wildly fluctuating
second moment

22. … proposed an α-stable cure ?
30 July 2014 22
Tails of stable df
Data

23. Auroral physics: fat tails
pdf of AE
Magnetometer time series
AU
AL
AE=AU-AL
Hnat et al, NPG [2004]
S&P 500
Mantegna & Stanley

24. White noise: fast fluctuations
30 July 2014 24
( ) ( ) ( ) ( )t t dt      


  
Delta correlated
White noise

25. A new puzzle: the Nile …
Hurst (1880-1978) studied this dataset from
point of view of design of “large and long
term over-year storage … ‘century storage’”30 July 2014 25
600 700 800 900 1000 1100 1200 1300
9
10
11
12
13
14
15
Annual minimum level of Nile: 622-1284
Annualminimum:
Time in years

26. Ideal reservoir
• Average influx over
years - we need to ensure annual released
volume equals mean influx:
Accumulated deviation
of the influx from the
mean:
30 July 2014 26
1
1
( )
t
t

 



   
1
) { ( )( },
t
u
uX t   

   

27. Range:
Standard deviation:
Plot against interval (loglog).
In white Gaussian case Feller:
(Rescaled) range
30 July 2014 27
R
S
0 0max ) min , )( (,t tx xtR t      
1
S



1/2
/ ~R S 

28. Hurst found anomalous growth of R/S,
exponent J about 0.7
Hurst’s effect
30 July 2014 28
/ ~ J
R S 
Hurst, Nature, 1957
Bold ine, mean
value over
datasets.
Circles, trials from
Hurst’s own model.

29. Joseph effect
30 July 2014 29

30. Joseph effect
30 July 2014 30

31. Joseph formalised
30 July 2014 31
2 1
( ) d
k ck 
0 1/ 2d 
( )
k
k
k


 ( )
k
k
k


 
Beran, “Statistics for long
Memory processes”, 1994
Fast decaying autocorrelation
e.g. white noise, delta correlated;
or AR(1), exponentially correlated
Short range dependence (SRD) Long range dependence (LRD)

32. Modelling heavy tails and LRD
30 July 2014 32
Mandelbrot and Wallis, 1969
Fractional hyperbolic noise

33. Linear Fractional Stable Motion:
combines heavy tails & long range
dependence
• C.f. Mandelbrot’s fractional Brownian motion
but integrates -stable “Levy” (not Gaussian)
noise (e.g. Samarodnitsky & Taqqu).30 July 2014 , 33
1 1
1
( ) ( ) ( ) ( )
H H
H H R
X t C t s s dL s 
  
  
 
    
 
   
Memory kernel: d
measures LRD α-stable jump:
heavy tails
1
d H

 

34. LFSM in Markovian (d=0), but
heavy tailed, limit = stable motion
30 July 2014 34
1
( ) ( )H H R
X t C L s  

  
Memory kernel =1, here α-stable jump:
heavy tails
1
H



35. LFSM in long range dependent,
light tailed limit, fractional
Brownian motion.
30 July 2014 35
1/2
1/2
2,2 2
1
( ) ( ) ( ) ( )
H
H R
H
HX t C t s s dL s
 
   
 

   
Memory kernel:
Joseph effect Gaussian jump
2
1
d H 

36. Bursts
30 July 2014 36
2
1
) '( '
t
t
s x t dt 
2
1
'
t
t
T dt 

37. log s
log
P(T)
log
P()
logT
log 
Poynting flux in solar wind plasma from NASA
Wind Spacecraft at Earth-Sun L1 point
Freeman, Watkins & Riley [PRE, 2000].
log
P(s) size
length
waiting time
some bursts we made earlier
Data

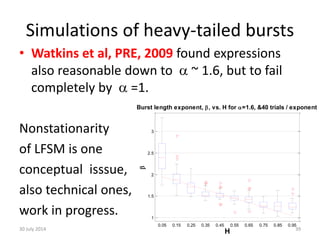
38. Simulations of light-tailed bursts
• Power laws for pdf of burst size s, and duration T
predicted to have exponents =-2/(1+H) & =2-H
respectively [Watkins et al, Phys. Rev. E, 2009 ].
• Good agreement in Gaussian (fBm) limit: Confirmed
findings of Carbone et al [PRE, 2004] & Rypdal and
Rypdal [PRE, 2008].
30 July 2014 38
=-2/(1+H) =2-H
gamma
H H
beta

39. Simulations of heavy-tailed bursts
• Watkins et al, PRE, 2009 found expressions
also reasonable down to  ~ 1.6, but to fail
completely by  =1.
Nonstationarity
of LFSM is one
conceptual isssue,
also technical ones,
work in progress.
30 July 2014 39
1
1.5
2
2.5
3
0.05 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 0.95
H
Burst length exponent, , vs. H for =1.6, &40 trials / exponent


40. Other approaches: multifractals
May wish for an even more volatile time series--
- a multifractal then more useful. Dependence
sometimes seen not in amplitude but in the
unsigned magnitudes, counterpart of the
“volatility bunching” seen in finance.
30 July 2014 40
0 0.5 1 1.5 2 2.5 3 3.5 4
x 10
4
-600
-400
-200
0
200
400
600
increments,r
First differences of AE index January-June 1979
-100 -80 -60 -40 -20 0 20 40 60 80 100
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
lag
acf
AE data: acf of returns
-100 -80 -60 -40 -20 0 20 40 60 80 100
-0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
lag
acf
AE data: acf of squared returns

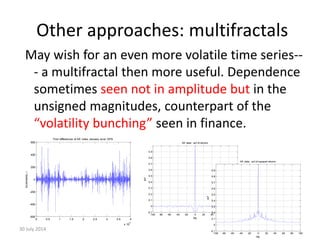
41. Recap
• Some natural severe events may be rare extremes, tractable with EVT
[e.g. Coles, 2001], adapted to allow correlation if present.
• Others may belong to a different class [studied by Mandelbrot] “Bursty”
time series may show comparatively frequent high amplitude events,
and/or long range correlations between successive values. The frequent
large values due to the first of these effects can give rise to an burst
composed of successive wild events. Conversely, long range dependence,
even in a light-tailed Gaussian model, can integrate ``mild” events into a
extreme burst
• I showed a standard statistical time series model, linear fractional stable
motion (LFSM), which allows these two effects to be varied independently.
Presented results from a preliminary study of such bursts [Watkins et al,
PRE, 2009].
• Other options for burst scaling modelling including multiplicative cascades
(such as multifractals).
41

42. Thank many people including Tim Graves (Cambridge),
Dan Credgington (now Cambridge) , Sam Rosenberg (Now
Barclays Capital), Christian Franzke (BAS), Bogdan Hnat
(Warwick), Sandra Chapman (Warwick), Nicola Longden
(BAS), Mervyn Freeman (BAS), Bobby Gramacy (Chicago),
Dave Stainforth and Lenny Smith (LSE), and my very
patient GRL editor: Paul Williams
Watkins et al, Space Sci. Rev., 121, 271-284 (2005)
Watkins et al, Phys. Rev. E 79, 041124 (2009a)
Watkins et al, Phys. Rev. Lett. , 103, 039501 (2009b)
Franzke et al, Phil Trans Roy Soc, (2012)
Watkins et al, AGU Hyderabad Chapman Conference Proceedings (2012)
Watkins, GRL Frontiers, 2013, doi: 10.1002/grl.50103

43. Spares
30 July 2014 43

44. Hurst’s model(s)
30 July 2014 44
Obituary

45. Compound extremes ...
30 July 2014 45

46. Compound extremes ...
30 July 2014 46

47. Compound extremes ...
30 July 2014 47