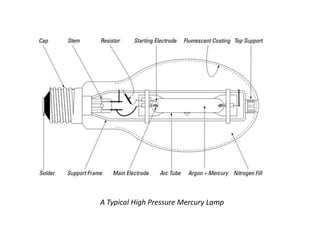
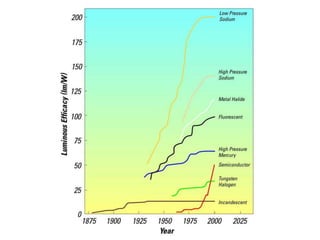
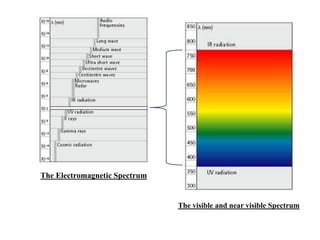
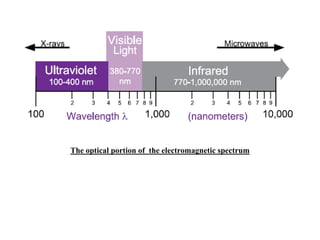
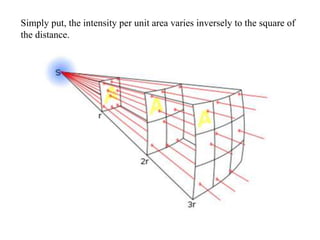
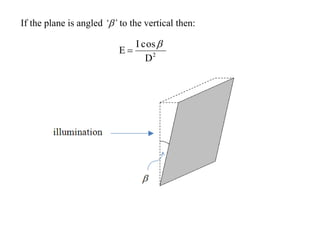
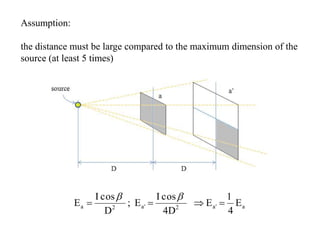
This document discusses illumination engineering and provides definitions and formulas for key terms. It describes: 1. The electromagnetic spectrum and visible light spectrum. 2. Terms like luminous intensity, luminous flux, illuminance, luminous exitance, and luminance and their definitions and relationships. 3. How to calculate illuminance on surfaces using the inverse square law and other formulas, accounting for factors like source intensity, distance, and angle to the surface. 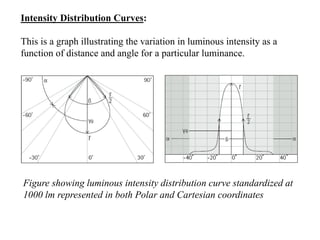4. Intensity distribution curves and how they illustrate light output as a function of angle. 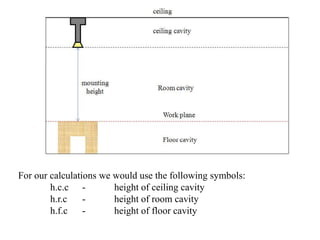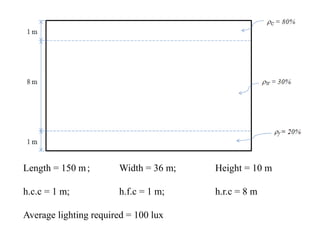5. The zonal cavity method for lighting layout and design, which divides a room into cavities and calculates light levels based on factors like room dimensions

1. ECNG 3015
Industrial and Commercial Electrical
Systems
Lecturer
Prof Chandrabhan Sharma
# 8
Illumination Engineering

2. ILLUMINATION ENGINEERING

3. The Electromagnetic Spectrum
The visible and near visible Spectrum

4. The optical portion of the electromagnetic spectrum

5. Equal-energy white light is defined as the simultaneous presence of all
wavelengths within the visible spectrum in equal energy amounts.
Incandescent lamps - stronger in reds and yellows.
Standard Fluorescent - weak in blue and green.
Mercury - consists of only blue, green and yellow-green.
Sodium - strongest in yellow.
Sunlight – almost uniform but deficient in blue and violet.
However, to the eye they all appear (except Na) to produce white light
and it is only when colours are viewed in these lights that their
deficiency can be detected.

6. A Typical High Pressure Mercury Lamp

8. Symbol Concept English Unit Metric Unit
I Luminous Intensity
or Candle Power
Candela (cd) Candela (cd)
 Luminous Flux Lumen (lm) Lumen (lm)
E Illuminance Lumen/ft2
(footcandle [fc])
Lumen/m2
(lux or lx)
M Luminous Exitance Lumen/ft2 Lumen/m2
L Luminance cd/ft2
(footlambert)
cd/m2 (nit)
Q Quantity of Light lm.s lm.s
ENTITIES IN ILLUMINATION ENGINEERING

9. Luminous flux corresponds to the power in a radiation system.
Quantity of light corresponds to the energy in the system.
 lumens  watt
lm.s  joule (watt.sec)
1 footlambert  1/ cd/ft2
1 footcandle  10.76 lux
The footcandle is the illuminance of a candle placed 1 ft away on
an area 1ft2

10. TERMS AND THEIR DEFINITIONS:
1. Luminous Intensity (I) -:
Initially, a luminous intensity of 1 candela was the strength of light
given off by the burning of a spermaceti candle of a specific weight
burning at a specific rate. Presently, the brightness of a black body
radiator at a temperature of solidification of platinum is 60 cd/cm2
(relative).
2. Luminous flux () -:
A luminous flux of one lumen is the rate at which luminous energy
is incident on a 1 m2 surface placed 1 m away from a uniform point
source of 1 cd intensity.
(lumens)2
d
AI


11. where
A = area of the surface  to the direction of luminous intensity
d = diameter of the source
I = intensity of the source
 for a UNIT SPHERE; a uniform source of 1 cd emits a luminous
flux of 4 lumens.


4)1(4
r4sphereofArea
2
2


lumens4
4
2



d
I
 the luminous flux is the ‘amount of light’

12. 3. Illuminance (E) -:
As luminous flux () travels outwards from a source, it ultimately
impinges on objects where it is reflected, transmitted and absorbed.
The Illuminance (E) on a surface is the density of luminous flux
incident on that surface, or;
areasurfacewhere, 

 A
A
E
2
2
d
I
A
d
AI
E 
 An illuminance of 1 lux is established when 1 lumen is
incident on 1 m2
lux  lumens/m2  cd/m2

13. 4. Luminous Exitance (M) -:
The luminous flux density leaving a surface is the LUMINOUS
EXITANCE (M) of that surface.
The density of the luminous intensity leaving a surface in a
particular direction is the LUMINANCE (L) of that surface.
)Brightness(
viewingofArea
IntensityLuminous
L 

14. Example:
Assume the unit sphere (with 1 cd intensity source) given before is
translucent. It has the property of transmitting 80% of the luminous
flux it receives and absorbing the remaining 20% (none is
reflected).
Thus the luminous flux leaving the sphere:
= (0.8)(4) lm = 3.2 lm
Luminous exitance (M) of the sphere:
2
2
lm/m0.8Eor 
d
I2
2
lm/m0.8
4
3.2
M 
r


15. Now, if we stand back from the sphere, the sphere would appear as
a source of light of luminous intensity (I) of 0.8 cd and area  m2.
lm.s192)2.3)(60(Q  
2
cd/m
8.0
LisspheretheofLuminancethe


The quality of light (Q) from surface is the luminous energy from
that surface.
For the sphere with it’s 80% transmittance, the quality of light
emitted is 1 minute is

16. Question 1
The upper hemisphere of a glass globe is silvered on the inside so
that 90% of the lumen hitting it is reflected to the lower
hemisphere. The latter is translucent glass and has a transmittance
of 75% and absorptance of 25%. The sphere has a radius of 0.5 m
with a 100 cd lamp at it’s centre. The lamp emits lumens uniformly
in all directions as does the lower hemisphere. Find the illuminance
on the inside of the lower hemisphere and luminous exitance and
luminance of the outside of the lower hemisphere.

17. Soln:
(a) The luminous flux emitted by the source (per unit sphere) is
1 cd source  4 lumens
lm180)200)(9.0(reflectedQuantity  
of which
200 lm goes towards the silvered surface
AND 200 lm goes downwards.
lm400100.4  
lm380)180200(
)(downwardsfluxluminousorquantityTotal
 
 d
lux760
)5.0(2
380
)(EeIlluminanc 2





A
d

18. Luminous flux  towards surface = 380 lm
transmitted = 0.75 x 380 lm = 285 lm
Area
mittedflux transLuminous
(M)exitanceLuminous(b) 
2
2
2
lm/m570
)hemisphereofarear2and0.5rewher
0.5
285
2
285
M






r

19. At a distance, the source would appear as a source of
Area
directionparticularainintensityLuminous
(L)Luminance(c) 
cd
2
285


where (2 is half of the unit circle)
At a distance the unit sphere appears as a unit circle
Note : 1 cd source emits 2 lm in a unit hemisphere
0.25
0.5)(r25.0xdistanceatsphereofArea 2



 r
22
cd/m
570
cd/m
0.25
142.5
L


References:
1. IES – Illumination Engineering Society (of North America)
2. ESI – Equivalent Sphere Illumination
sphere)unit(ESIcd/m
570
r
M
Lor 2
2



20. Inverse Square Law: (I.S.L)
As was stated before, a source of luminous intensity (I) of 1 cd will emit
a luminous flux of 4 lumens.
If the unit sphere is replaced by a sphere of radius ‘r’, the same 1 cd
source has to now light up an area of 4 r2.






 22
r4
4
r
1
sphereunitaofthattosurfacenewonlightofRatio


A
A
A
1
x
D
I
E 2
1



(m)planereceivingthetosourcethefromdistanceD
(cd)intensityI
luxEwhere
D
I
EstatesISL 2





21. Simply put, the intensity per unit area varies inversely to the square of
the distance.

22. If the plane is angled ‘’ to the vertical then:
D
cosI
E 2



23. Assumption:
the distance must be large compared to the maximum dimension of the
source (at least 5 times)
aa'2a'2a E
4
1
E
4D
cosI
E;
D
cosI
E 


24. Example 1:
lux0.7
5015
cosI
E 22




A globe street light has a uniform intensity of 2000 cd. Find the
illuminance on the stop sign.
Soln: From geometry  = 16.7

25. Illumination on a Horizontal Plane:
2
3
horizontalP
2
3
222P
h
)cos(I
E
h
)cos(I
dh
)cos(I
D
)cos(I
Ethen






Let h – height of luminaire above plane
d – horizontal distance to point of observation

26. where
EP horizontal - illumination at point P (lux)
I( ) - intensity of the source in the direction of P (i.e.  from
the vertical
D – distance from the light centre of the source to the point P
 - the angle between the normal to the receiving surface at P
and the distance d (in this case  =  )

27. Example 2:
cm56.25cm
2
15
surfacelightofArea
:Soln
22
2
 






A flat circular fixture 15 cm in diameter is mounted on a ceiling in a
recreation room. It’s luminance (luminous flux) in the direction of point
P on a table is 40 cd/m2. Find its intensity in the direction of P and the
illuminance on the table at P.

28. viewingofAreaAewher;
A
I
Luminance 
AcosxLI 
cd3918.5)(56.3cosx56.25x40)(I  
lux24.167
13
56.33918.5cos
D
cosI
E 2




lux3.167
2
56.33918.5cos
h
cos)(I
Eor 2
3
2
3





29. Intensity Distribution Curves:
This is a graph illustrating the variation in luminous intensity as a
function of distance and angle for a particular luminance.
Figure showing luminous intensity distribution curve standardized at
1000 lm represented in both Polar and Cartesian coordinates

30. Lighting Layout and Design:
1. CHOICE OF LAMP – see attachment
The entire lighting system relies on the dimensions and finish of
the room surfaces and room to accurately determine light levels.
2. POINT BY POINT METHOD
Using equations developed before, the illumination at specific
‘points’ in a room are calculated. By using basic trigonometry
the designer can predict light levels on both horizontal and
vertical surfaces.
3. ZONAL CAVITY METHOD – (Lumen method)
In this case the room is divided into three separate cavities
- ceiling cavity
- room cavity
- floor cavity

31. For our calculations we would use the following symbols:
h.c.c - height of ceiling cavity
h.r.c - height of room cavity
h.f.c - height of floor cavity

32. Theory:
Light from a lamp is reflected by all surfaces by varying amounts.
These multiple reflections from the room surfaces all add to produce
light on the task.
Before start of the design, determine:
1. Room dimensions
2. Room finishes (i.e. reflectance) of:
(a) ceilings
(b) walls
(c) floors
3. Lamp characteristics
4. Luminaire characteristics

33. 5. Environmental effects e.g.
(a) dust and dirt
(b) temperature
6. Lighting system maintenance plan
Recall that 100 lux average illumination over an area of 100 m2 will
require 10,000 lumens to be directed on the task.
Room Finish:
Room surface colour affects the light level in the room. This also
applies to furnishings within the room, drapery materials and also
carpeting used.

34. BASIC FORMULA (ZONAL CAVITY)
M.F.xC.U.x
AxE
N


where
N = No. of fittings needed
E = the required illumination in (Lux)
A = working area in m2
 = flux produced per fitting (lumens)
C.U. = coefficient of utilization
M.F. = maintenance factor

35. Coefficient of Utilization (C.U.)
This factor allows for losses incurred by absorption of light by walls,
ceiling, floor, furniture, etc.
sourcefromemittedlight
surfacedilluminateon theincidentlight
C.U. 
Maintenance Factor(M.F.)
cleanfittingsandnewlampswitheilluminanc
given timeanyateilluminanc
M.F. 
L.D.DxL.L.DM.F.
where
L.L.D = lamp lumen depreciation
L.D.D = luminaire dirt depreciation

36. Example
Determine the no. of fixtures required to light an area 50,000 m2 to
100 lux average level.
Given: C.U. = 0.74
L.L.D = 90%
L.D.D = 85%
Lumens/lamp = 50,000
Lamps/luminaire = 1
177
0.85x0.9x0.74x50,000
50,000x100
N 

37. STEPS IN DESIGN LAYOUT:
1. Determine what task or tasks are to be performed in the area. This
will determine the quality and quantity of light needed.
2. Determine what light source should be used.
3. Determine the environmental conditions which will prevail in the
area. (This will affect the M.F.)
4. Determine the physical and operating characteristics of the area and
how it will be used. This includes:
(a) Room dimensions
(b) Room reflectance values
(c) h.c.c, h.r.c and h.f.c
(d) Time duration during which room will be in use (24 hrs,
12 hrs, 8 hrs, etc.).

38. 5. Select the luminaire to be used. This will be affected by:
(a) mounting height
(b) lamp type
(c) L.D.D
(d) physical mounting restrictions (pendant, recessed,
enclosed, open)
(e) maintenance required (cleaning of reflectors)
(f) cost, size, weight
(g) aesthetics
6. Determine the M.F. for luminance.
7. Determine the cavity ratios for the area. This is given by:

39. 9. Determine the C.U.
10. Compute the no. of luminaire required using:
determinedbeingisratioon whichdependingh.f.corh.r.ch.c.c.,hwhere
idthLength x W
width)Roomlength(Roomhx5
RatioCavity



M.F.xC.U.x
AxE
N



40. Example:
It is required to maintain the average illumination in a room at 100
lux. The dimensions of the room are (L x W x H) 150 x 36 x 10 m.
The luminaire to be used is a wide distribution type (No 11)
Lumalux, LV 400 W, Hg HID lamp. The environmental conditions
are dirty, category V, with the lamps being cleaned every six months.
Initial lumens output of the lamp is 50,000 lms and L.L.D at re-
lamping is 50%. The work plane is 1 m above ground and the
luminaire is pendant type hanging 1 m from the ceiling. Determine
the number of luminaire required and give a proposed luminaire
arrangement. Room reflectance are
wall = 30%
ceiling = 80%
floor = 20%

41. Length = 150 m; Width = 36 m; Height = 10 m
h.c.c = 1 m; h.f.c = 1 m; h.r.c = 8 m
Average lighting required = 100 lux

42. # of lumens/luminaire = 50,000
From Fig 13-15 L.D.D = 0.85
and L.L.D = 0.5 (given)
 M.F = L.D.D x L.L.D = 0.425
M.F.xC.U.x
AxE
NBut


Required to determine C.U.
1. Determine Cavity Ratios:
17.0
36x150
36)(150x1x5
RatioCavityCeiling(C.C.R) 



43. 37.1
36x150
36)(150x8x5
RatioCavityRoom(R.C.R) 


17.0
36x150
36)(150x8x5
RatioCavityFloor(F.C.R) 


From Figs 13 - 11A and 13 – 11B we obtain:
Effective ceiling cavity reflectance = cc =76.6%
76.6%or766.076
0.2
72)-(76x0.03
30%and80%0.17,C.C.R
usingioninterpolatlinearbyderivedwasThis
cc
wc









44. Effective floor cavity reflectance = fc =19%
(By linear extrapolation)
cc=76.6%, w=30% and RCR = 1.37
From table 13-12A (for fc=20%)  C.U. = 0.475 (linear extrapolation)
From Fig 13-13 we obtain C.U, for fc =19%
cc =76.6%; w =30%; R.C.R = 1.37 (using fc =10% curve)
 for cc =70% and w =30% the factor = 0.948
Also, for cc =80% and w =30% the factor = 0.94
Multiplication factor for cc =76.6%

45. 943.0
10
0.94-0.948
6.6948.0
is76.6%using10%atfactor cc













 
994.0943.0
10
0.943-1
9
is10%using19%atfactor fc







 
 C.U. (fc at 19%) = 0.475 x 0.994 = 47.2%
luminaire54or53.7
0.5x0.85x0.472x50,000
36x150x100
Nand 

46.  The number of luminaire in each row is:
2
m100
54
36x150
luminaireperdilluminatebetoareaaveragethe


m10100luminaireperspacingaveragetheand 
46.3
10
36
m)(36Width
15
10
150
m)(150lengthFor


 Actual No. to be installed = 15 x 4 = 60

47. Check From data sheet for luminaire # 11 (Fig 13-12A)
1.3
HeightMounting
)(SSpacingMaximum max

o.k.isondistributihetm10SBut
10.48x1.3HeightMountingx1.3Smax

