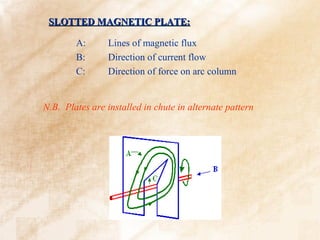
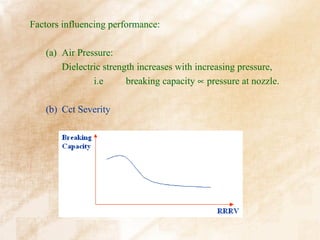
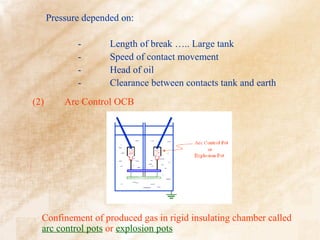
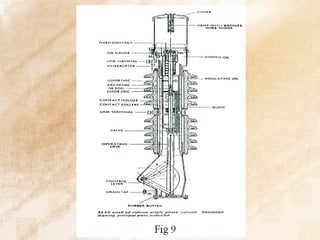
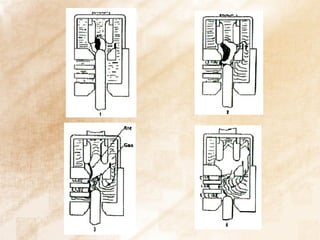
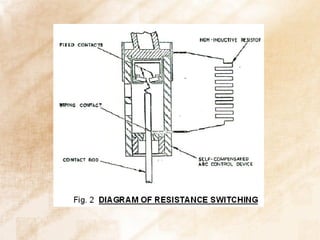
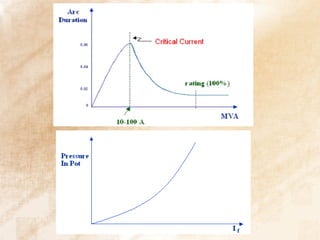
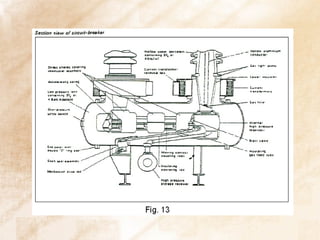
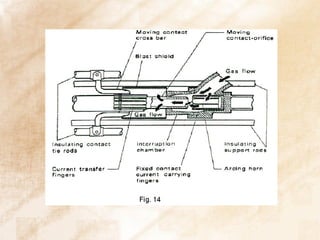
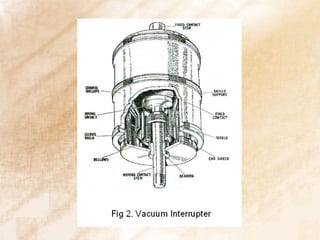
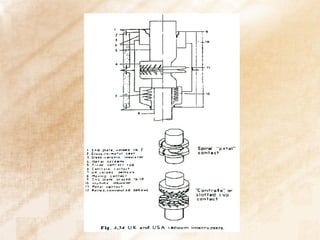
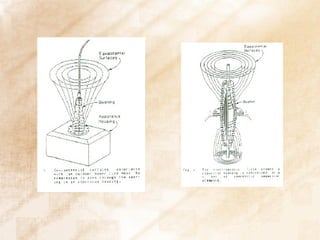
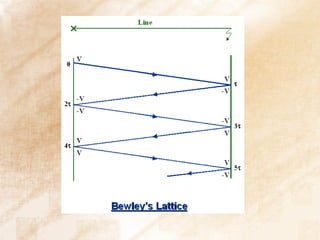
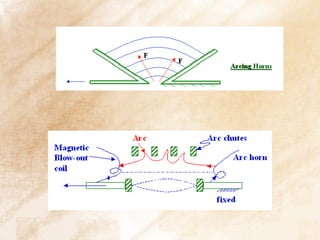
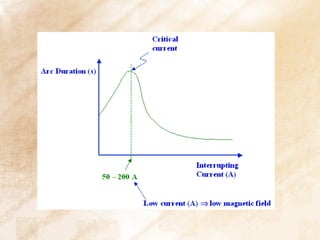
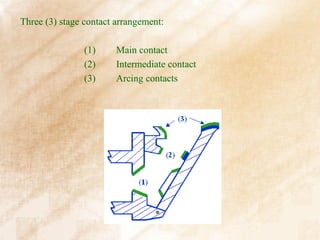
The document discusses switchgear technology and circuit breaker operation. It covers several topics in 3 sentences or less: Static welding of contacts can be overcome by increasing contact force and occurs at lower currents than dynamic welding. Arc interruption requires increasing plasma resistance at current zero and ensuring dielectric strength increases faster than electric stress. In a double frequency circuit, the voltages on the two circuits after opening will be proportional to the inductances in each circuit divided by the total inductance.

1. ECNG 6509
Switchgear Technology
Prof Chandrabhan Sharma A

2. SWITCHGEAR TECHNOLOGY
SWITCHGEAR
Contacts → Theory of Conduction
(i) Metallic → electrons
(ii) Electrolytic → ions
(iii) Gas Discharge → electrons and ions
Regions for electron flow are:
- Areas in metallic contact
- Areas Quasimetallic contact < 20 Å
- Areas fritting of contact film → thin enough to allow
dielectric breakdown.

3. POINTS OF CONTACT
Constriction Resistance ≙ resistance of a single contact spot.
* Contacts exposed to a constant current run hotter that similar
contacts carrying similar current but subjected to occasional
surges
→ Contact softening → reduce R

4. STATIC WELDING
For Tmelt > To
V = 3 x 10-4 Tmelt
or V ∝ Tmelt where V = welding voltage
∴ The welding voltage on s/c ∝ melting temperature of the material.
Also static welding is a fn (contact force)
ρ πH Where:
Rc = H = hardness
2 F
F = force
k 1
For a particular metal contact resistance = R c = α
F F

5. ∴ For a given current I
V = IRc ∝Tmelt
1
or Tmelt ∝ F½ ∝
F
Voltage across a contact for a given current is greater at lower contact
forces.
∴Static welding occurs at lower currents.
Rule of Thumb:
Static welding could usually be overcome by increasing contact force.

6. DYNAMIC WELDING (during contact bounce)
Weld caused by coalescence of pools of molten metal at the base of shorts
arcs produced by contact separation during bounce.
Process of Contact Making:
- Initial Spark-over → dielectric breakdown
- First touch
- Growth of contact force
- Reduction of (3) static level

7. PHYSICS OF ARCS IN C.B.
C.B. has two (2) stable conditions
(a) Close ⇒ Ƶc ≈ 0
(b) Open ⇒ Ƶc ≈ ∞
∴ Ƶc goes from 0 → ∞ in cycles.
Too long time ⇒ release of large energy
Too short ⇒ switching overvoltages.
For AC interruption, switching is done at natural current zero.

8. Two (2) requirements for AC interruption:
(a) Increase plasma resistance exponentially in region of
current zero.
(b) Ensure dielectric strength of arc path increases faster than
electric stress. (Slepian’s Theory)
Initial emission of electrons may be due to:
(a) Thermionic → increase in electrode temperature
(b) Field → high voltage gradient at cathode

9. A.C. CIRCUIT BREAKERS
Two (2) types: (i) High Pressure Arcs
(ii) Vacuum
High Pressure Arcs:
* Unable to stop arc.
Three (3) distinct regions
(i) Cathode
(ii) Arc Column
(iii) Anode
(i) & (iii) unimportant in arc extinction.

10. (1) Thermal Ionization
Degree of ionization, xi due to thermal ionization given by
Saha’s equation:
 x i2  W 
- i 
= AT 2 e  kT 
1
P 2
1 - x i 
 
P – Gas pressure Wi – ionization potential
A – gas constant k – Boltzmann’s constant
T – absolute temperature
(2) Ionization by collision due to high electric gradients

11. MAGNETIC PHENOMENA IN ARCS
Similarities of Arc and solid conductor …..
(a) Circumferential fields
(b) Transverse Fields
Lateral forces set up similar to that of a current in a solid
conductor. Initially a straight arc will always bow under
the influence of self magnetic field.

12. STATIC ARC CHARACTERISTICS
Model 1: Assume:
Current Density (J) constant
heat loss/unit area (k) = constant
∴ Area = (2πr)(1)
∴ Heat loss = W = 2πrk
Total current = πr2J = i
⇒ r = √i
But energy liberated = vi = Jπr2(v) = E
For balance W=E
⇒ 2πrk = Jπr2v
or v ∝ 1/r ∝ 1/ √i
Holds true for ‘i’ small

13. Model 2:
Current density = constant
heat loss ∝ cross-sectional area
i ∝ πr2
E = vi = W
W ∝ πr2 (heat loss)
∴ vi = i
⇒W∝i
v= constant

14. Slepian’ Theory
Energy Balance:
Cassie suggests that for interruption
Energy loss from arc > Energy input to arc

15. VACUUM ARCS
Two (2) Forms
(a) Diffuse Arc
(b) Constricted Arc
Once arc falls into constricted mode, interruption fails.

16. DYNAMIC ARC COLUMN
The dynamic arc model is of this form
i 1
= = f (W, N, t)
e R
Where i – instantaneous current
e – instantaneous arc voltage gradient
R - instantaneous arc resistance/length
W – power input per unit length
N – power loss per unit length
f (t) – effects of thermal time lag of conductance

17. 1
Also, = f (Q) where Q - energy content/unit length
R
From the 1st Law of Thermodynamics :
dQ
W=N+ + w ; where w - work done by arc
dt
neglecting w
⇒ Q = ∫ (W − N)dt
1
and = f (Q) = f [ ∫(W − N)dt] ..............................(1)
R
 f ' (Q)  dQ f ' (Q)
R d( 1 R ) =   = (W − N) ................................(2)
 f (Q)  dt f (Q)

18. Cassie’s Model
Assumptions:
(1) Column cylindrical, p and q (energy/unit volume) constant.
(2) At constant arc temperature i ∝ A (cross-sectional area).
(3) Power loss/unit volume (λ) = constant or power loss ∝ A.
ρ
R= ; Q =qA
A
1 A Q
∴ = f (Q) = =
R ρ qρ
1
and f ' (Q) =
qρ

19. From assumption (3) ⇒ N = λ.A
It flows from equation (2) that
1
d 1
R ( R ) = Q qρ (e.i − λA).............................(3)
dt
qρ
2
1 e
= ( − λA)
Q R
λ e 
2
=  
 λAR − 1
q 
λ e 
2
=  − 1
q  λρ 


20. In static conditions the per unit volume power loss λ = per unit volume input
∴ e i = N = λA
e2
or = λA
R
e = λAR = λp = const = e o
⇒ constant voltage characteristic at s.s.
d 1 λ  e2 
R ( R ) =  2 −1...........................(4)
dt q  eo



1  dR  λ  e2 
or   = 1 − 2 
R  dt  q  e o 
 
dR
at steady state e = e o and =0
dt

21. Alternatively (3) can be written
1 dR 1
= ( λA − e i )
R dt Q
dR ARλ ARλ λ
if i suddenly goes to zero then = = =R
dt Q qA q
dR R R
= =
dt ( q λ ) θ
where θ = (q λ )
or R = R oe( t θ )
where θ = time constant for conductivity

22. CIRCUIT CONSTANTS
Single Frequency:
At 1st current zero: Applying Kirchhoff Law:
di
Vm cos ωt = L + VC ..........................(1)
dt
1 dVC
But VC = ∫ i dt ⇒ i =C
C dt
Sub. into (1)
d 2 VC
LC 2 + VC = Vm cos ωt...........................(2)
dt

23. d 2 VC VC Vm
divide by LC ⇒ 2
+ = cos ωt......................(3)
dt LC LC
1 d 2 VC
let ω =
2
0 ⇒ + ω0 VC = ω0 Vm cos ωt......................(4)
2 2
LC dt 2
Taking Laplace Transform
 s 
⇒ s 2 VC (s) + sVC (0) + VC (0) + ω 0 VC (s) = ω 0 Vm  2
' 2 2
2
..........(5)
s + ω 
Solving for VC (s)
 s   s  VC (0) '
⇒ VC (s) = ω0 Vm  2
2
2 
+ VC (0)  2 2
+ 2 ..........(6)
 (s + ω )(s + ω 0 )   s + ω0  s + ω0
2 2 2
At t = 0- ⇒ i=0 (first current zero)
1
∴ dV(0) = 0 =   i (t)
C

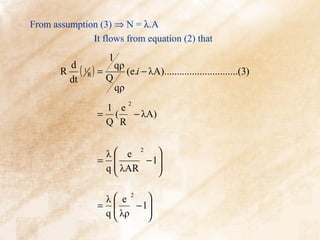
24. Also VC(0) = arc voltage ; which is negligible
 2
s ω0 
⇒ VC (s) = Vm  2 2 
.......................(7)
 (s + ω )(s + ω0 ) 
2 2
From partial fraction analysis:
s 1  s s 
= 2 2  2
− 2 2 
(s + ω )(s + ω0 ) (ω0 − ω )  (s + ω ) (s + ω0 ) 
2 2 2 2 2
Sub into (7)
ω02
 s s 
VC (s) = Vm 2  − 2 2 
(ω0 − ω 2 )  (s 2 + ω 2 ) (s + ω0 ) 
Taking inverse:
2
ω0 1
VC (t) = 2 Vm [ cos ωt - cos ω0 t ] ; where ω0 =
(ω0 − ω 2 ) LC

25. For most circuits: C << small and ω0 >> ω
2
ω0
∴ 2 →1
(ω0 − ω )
2
∴ VC (t) = Vm [ cos ωt - cos ω0 t ]
Also for period of analysis, the power terms is constant w.r.t. ω0
∴ equation becomes VC (t) = Vm [1 - cos ω0 t ]
(1) Max. restrike voltage = VC(max)(t) = 2 Vm
π
which occurs at t = or π LC
ω0
1
and f 0 =
2π LC

26. Rate of Rise of Recovery Voltage [RRRV]
dVC
RRRV = (kV/µs)
dt max
2Vm
⇒ RRRV = (kV/µs)
t
π 2V ω
when t = ⇒ RRRV = m 0
ω0 π
dVC
Aside : = Vm ω0 sin ω0 t
dt
dVC π
For ⇒ Vm ω0 sin ω0 t = 0 ⇒ sin ω0 t = 0 or t =
dt maximum ω0

27. CIRCUIT CONSTANTS
Double Frequency:
Before opening C.B.:
 L2 
VC = 
 L + L Vm

 1 2 
After opening the switch, two circuits are formed as seen on
the next slide

28. 1
Natural frequency ω0 =
L1C1
and
1
Natural frequency ω1 =
L 2C2
 L2 
Where VC1 = VC2 =
 L + L Vm

 1 2 

30. Using Principle of Superposition :
E Vp
If = = (purely reactive i.e. R = 0)
Z ω(L1 + L 2 )
E Vp
∴ If (t) = = sin ωt
Z ω(L1 + L 2 )
 L2 
and VC 2 = Vp 
L +L 
 1 2 

31. For circuit interruption at current zero:
Vp
∴ i (s) =
(L1 + L 2 )s 2
In ‘s’ domain:

32. But VC(s) = i(s) Ƶ(s)
s/C1
where Z(s) = 2 (operational impedance)
s + (1 / L1C1 )
sL1/L1C1
=
s 2 + (1 / L1C1 )
1 2
L1s ω1
set ω1 = ⇒ Z(s) = 2
L1C1 s + ω1 2
 Vp   L1s ω1 
2
 L1   2
ω1 
⇒ VC (s) = 
 (L + L )s 2   s 2 + ω 2 
  = 
 L + L   s(s + ω 2 ) 
Vp  2 
 1 2  1   1 2   1 

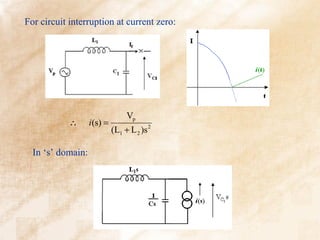
33. 2
ω1 1 s
But = − 2
s(s + ω1 ) s s + ω1
2 2 2
 L1   1 s 
∴ VC (s) = 
 L + L   s s + ω2 
Vp  − 2 
 1 2   1 
 L1 
⇒  L + L Vp [1 - cos ω1t ]
VC (t) =  
 1 2 
 L2 
From before VC ss = 
 L + L Vp cos ωt

 1 2 
 L2   L1 
∴ VC = VC ss + VT = 
L +L   L + L Vp [1 - cos ω1t ]
Vp cos ωt +  
 1 2   1 2 

34. For the other half of the circuit:
Vp
where I f = sin ωt
ω(L1 + L 2 )
Vp Vp
and ramp function for I f is i (t) = t or i (s) =
(L1 + L 2 ) (L1 + L 2 )s 2
Transformed circuit:

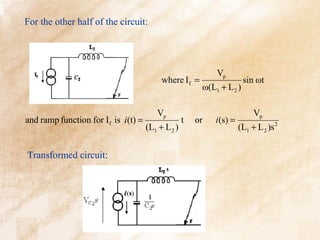
35. From circuit VC(s) = - i(s) Ƶ(s)
L 2 /C 2 L 2s ω 2 1
where Z(s) = = 2 2
and ω 2 =
L 2s + 1 / C 2s s + ω 2 2 L 2C 2
 L2   1 s 
∴ VC (s) = −
 L + L   s s + ω2 
Vp  − 2 
 1 2   2 
 L2 
⇒  L + L Vp [ cos ω 2 t - 1]
VC (t) =  
 1 2 
∴ VC 2 = VC ss + VT
 L2   L2 
 L + L Vp +  L + L Vp [ cos ω 2 t - 1]
=   
 1 2   1 2 

36.  L2 
=
 L + L Vp cos ω 2 t

 1 2 
 L2   L1   L2 
=
L +L Vp cos ωt + 
L +L Vp [1 - cos ω1t ] − 
 L + L Vp cos ω 2 t

 1 2   1 2   1 2 

37. BEWLEY’S LATTICE DIAGRAMS
Kilometric Fault Analysis:
L
Recall : Surge Impedance = Z 0 =
C
1
Velocity of propagation = v = ms-1
LC
If Ei = incident wave and Er = reflected wave then:
R - Z0
Er = Ei
R + Z0
Where R = terminating impedance

39. SWITCHGEAR MATERIALS
SELECTED MATERIAL SHOULD:
- Have the required technical properties
- Ease of working (forming, welding etc.)
- Low cost
- Stability and reliability
Enclosures:
Steel is the most common choice
- Mechanical strength
- Economics
Sheet thickness related to risk of “burn through”

40. Disadvantages:
- Magnetic
- Corrosion
CONDUCTING MATERIAL
- Must have low specific resistance
- Resist corrosion
Silver exhibits the lowest resistance but cost is prohibitive.!!
∴Silver coated contacts used:
(0.02 ∼ 0.05mm)
N.B. silver oxide is a conductor

41. Cu and Al also used.
Cu → Lower resistivity (than Al) and resists oxidation.
Chrome Cu → Alloy gives good compromise between strength
and hardness with good conductivity.
Tungsten/Cu → Alloy used for contact tips (Resists Arc erosion)*
* Main contact is silver/Cu.
Beryllium Cu → used for low tension springs (Non-magnetic)

42. Al is very soft and oxidizes readily.
Usually alloy with silicon used.
Use in Switchgear restricted to conductors, and busbars and
usually for low applications.
Caution:
- Cu/Al joints need special care.
- Electrochemical effect.

43. INSULATING MATERIALS
* Can be solid, liquid or gaseous:
Liquid & Gaseous: Includes air, SF6, oil and vacuum
Dielectric Strength:
x3 x3 ∞
Air → SF6 → Oil → Vacuum
SOLID DIELECTRICS:
Natural in Origin -: Mica, asbestos and slate
Derived from natural materials: Porcelain, paper and shellac varnishes
Newer materials : petrochemical derived, polymers, resins, films, plastics

44. BULK MATERIALS:
Glass (Pyrex), porcelain, epoxy and chalk, epoxy and
silica, dough moulding compound, polyurethane resin.
SHEET MATERIALS:
SRBP*, SRBF*, glass filled epoxy, glass filled polyester
SRB → synthetic resin bonded (paper, fabric)
THERMOPLASTICS:
Nylon, PVC, polyethylene, polytetra fluorethylene

45. Requirements for Solid Insulation:
- Long term stability of properties
- No measurable internal discharges at working voltage
- High tracking index
- Good mechanical strength
- Suitable for simple, low cost manufacturing.

46. AIR CIRCUIT BREAKERS
Arc Extinction: Natural deionization of gases by cooling action.
Stretching Arc ⇒ R ↑
As R ↑ ⇒ If ↓ and ∠θ → 0
⇒ i=0 when v=0
Rarc can be increased:
(1) Increasing arc length
(2) Cooling arc
(3) Splitting arc into several arcs

47. ARC CHUTES:
Two (2) Types:
- Insulated plate
- Metal plate
Controlling force that direct arc into chute given by natural
electromagnetic and thermal forces of the arc.
* Strong magnetic field provided by:
(i) External iron cct around the arc energised by turns
current fault current.
(ii) Internal iron cct in form of special shaped steel
plates.

49. Arc Chutes:
Perform three (3) functions
- Confinement of arc
- Magnetic control
- Rapid cooling of arc gases
Arc Splitter:

51. Three (3) stage contact arrangement:
(1) Main contact
(2) Intermediate contact
(3) Arcing contacts

52. SLOTTED MAGNETIC PLATE:
A: Lines of magnetic flux
B: Direction of current flow
C: Direction of force on arc column
N.B. Plates are installed in chute in alternate pattern

53. AIR BLAST C.B.
Types:
(1) Axial Blast
High voltages
(2) Radial Blast
(3) Cross Blast
Operation:
Interruption f (turbulence for cooling)
Dry compressed is an excellent dielectric.
Extinction occurs at 1st current zero.

54. Factors influencing performance:
(a) Air Pressure:
Dielectric strength increases with increasing pressure,
i.e breaking capacity ∝ pressure at nozzle.
(b) Cct Severity

55. (c) Distance Between Contacts
(d) Contact material → improvement (high B.P. material)
(e) Area of exit hole ↑
(f) Resistance switching (shunt)
- Reduce RRRV and restriking voltage (Vc)
- Reduce transient voltage
- Improve uniformity of voltage sharing → multibreak CB

56. PROS:
PROS
- No fire hazard
- Fast operation
- Suitable for rapid reclosing
- High rupturing capacity
- Low contact damage
- Easy access to contacts
CONS:
CONS
- Complete air system
- Complicated construction
- Specialized maintenance required
- Sensitive to RRRV
- Noisy

57. Shunt Resistors:
They are used for:
- Voltage grabbing
- Overvoltage suppression
- Reducing cct. severity
- Closing resistors for energizing long tx lines

58. OIL CIRCUIT BREAKER
Heat of arc immediately dissociates the surrounding oil into C and H2.
H2 has high heat conductivity hence cooling of arc and contacts cooling
so fast that re-ignition voltage is 5 – 10 times as for A.C.B.
Evolved gas:
H2 – 66% CH4 – 9%
C2H2 – 17% other – 8%
HIGHLY FLAMMABLE!!!!!!!
Volume Generated fn arc energy (≡Isc)

59. PROS:
PROS
- Oil is a spontaneous producer of H2
- Very good dielectric
- Very good thermal conductivity
CONS:
CONS
- Flammable
- H2 and oil can form an explosive mixture with air
- Carbon pollution of oil
See handout!

60. EVOLUTION OF OCB
(1) Plain Break
- No special Arc Extinction system
- Extinction due to turbulence and pressure

61. Pressure depended on:
- Length of break ….. Large tank
- Speed of contact movement
- Head of oil
- Clearance between contacts tank and earth
(2) Arc Control OCB
Confinement of produced gas in rigid insulating chamber called
arc control pots or explosion pots

62. (3) Minimum oil volume (Ref to Fig 9)
- Uses solid materials for insulating purposes and just
enough oil for arc quenching
- Oil tank is at system voltage hence ‘Live tank OCB’
nomenclature.
Three (3) types:
(i) Self blast type
(ii) External blast
(iii) Combination (i) and (ii)

67. BULK OIL
PROS:
- Simplicity of Construction
- High rupturing capacity
- Possibility of locating C.T. in bushing
CONS:
CONS
- Fire/explosion hazard
- Large volume of oil
- Contamination of oil → C
- Not suitable for indoor application
- Auto-reclosing inability
- Costly

68. MINIMUM OIL C.B.
PROS:
- Small quantity of oil
- Physically smaller
- Lower costs
- Easier access to contacts
CONS:
- Fire/explosion hazard
- Not good for repeated cycle of operation
- Frequent inspection of oil quality
- Greater contact damage
- Difficulty in locating C.T.s
- Lower rupturing capacity

69. SF6 BREAKERS
Properties:
- Colourless
- Odourless
- Non –toxic
- Non-flammable
- 5 times denser than air
- B.P. - 60 °C
- Thermal transfer coefficient = 1.6 x air
- Vapour pressure at 20 °C = 24 atm.
- Inert up to 150 °C
- Decomposes to: SF4, SF2, S, F2 (corrosive to
glass and metals in presence of moisture)
Interaction gives whitish powder of high insulating properties
→ contacts should be self wiping.

70. - Absence of C
- All decomposed gasses recombine within 10-6 – 10-7 s
after arc extinction
- Traces eliminated by activated Alumina
- At atmospheric pressure, dielectric strength ≈ 2.5 x air
SF6 strongly electronegative
SF6 + e → SF-6
SF6 + e → SF5 + F-
See figs 13 & 14 for Operation of SF6 breakers

73. VACUUM C.B.
- Vacuum arc persists because of metal atoms ejected
from cathode spot.
- Intensity of vapour jets ∝ intensity of current flow
⇒ plasma falls as current falls to zero.
- At current zero metal atoms and ions migrate and
condense on electrodes, shields and walls rapidly
deionising gap.
* Total absence of charge carriers ⇒ vacuum breaker has near ideal
withstand characteristics.

74. Fig. 1 Diagrammatic representation of vacuum arc

76. Applicable Properties of Vacuum
(i) Highest insulating strength known.
(ii) Interruption occurs at first current zero & dielectric
strength building up at rate 1000 x that of conventional
breakers.
(iii) At current zero, cathode spot extinguishes within 10-8 s

77. - The Diffuse arc has very high interrupting ability
- The Constricted arc has no interrupting ability
In order to ensure arc does not remain constricted, special
contacts have been designed.
(i) Spiral petal contact
(ii) Contrate contact
Depend for action on interaction of magnetic field of arc so
as to keep the arc in constant motion.

79. Contact materials:
materials
- Must not weld under fault conditions
- Must not chop on magnetizing current switching
- Must permit high dielectric recovery after interruption
- High conductivity
- Ease of manufacture
Used→ * Copper – Bismuth alloy
* Copper – chromium alloy

80. BUSHINGS
Capacitor (condenser) Type:
- Divide the dielectric insulation around the central
conductor into a large number of concentric
capacitors
- Results in a set of concentric capacitors which are
electrically in series → hence division of system
voltage in discrete steps
- Highest stress occurs at ends of conducting layers

83. Mechanical considerations:
considerations
- C.B. forces on a bushing far exceed the ‘G’ range of
recorded earthquakes!
- Transformers bushings do not experience this in normal
operation.
- Check on mechanical strength before installing spare
transformer bushing on C. B.

84. Bushing maintenance:
maintenance
- Visual inspection:
oil level; sight glass, broken housing etc.
- Field testing
- Power factor
Trending
- Capacitance
- Factory Repairs : water ingress
- Field Repairs: Very difficult and not normally done
- Change-out may be more economical

85. C. B. ratings:
ratings
- Rated V and I
- Rated frequency
- Breaking Capacity-: symmetrical and asymmetrical
- Making capacity
- Short-time current duration
- Operating duty.

86. TYPE TESTS
Applied to one of the batch at manufacture.
1. Mechanical
 2. Temperature Rise at rated current
 3. Impulse Voltage (1.2/50 µs wave)
 4. Short circuit (opening & closing)
 5. Short-time current → 2.5 x RMS rated s/c for 1 second
 6. Transient Restrike Voltage → form (1- cos)
 7. Contact Condition
 8. Critical current (OCB)
 9. 1φ opening of 3φ s/c
 10. Kilometric fault
 11. Load switching → R,L,C
 12. Transformer magnetizing Current

87. ROUTINE TESTS (All C.B.)
1. High Voltage
2. Mechanical
3. Resistance tests (ohm meter)
4. For O.C.B. → oil testing