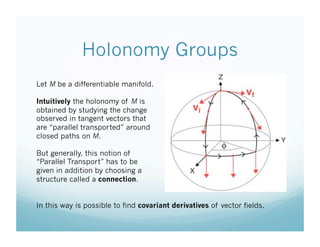
The document introduces holonomy and spin geometry, focusing on holonomy groups related to differentiable manifolds. It explains how holonomy is derived from parallel transport of tangent vectors around closed paths, requiring a connection structure. Additionally, it discusses the role of a Riemannian metric defined by a symmetric bilinear form at each point of the manifold.

1. Holonomy & Spin
Geometry
Introduction and some results

2. Holonomy Groups
Let M be a differentiable manifold.
Intuitively the holonomy of M is
obtained by studying the change
observed in tangent vectors that
are “parallel transported” around
closed paths on M.
But generally, this notion of
“Parallel Transport” has to be
given in addition by choosing a
structure called a connection.
In this way is possible to find covariant derivatives of vector fields.

3.  If g : M  T*M X T*M defines a (positive defined)
symmetric bilinear form for every point p of M, we
call it a (Riemmanian) metric
.