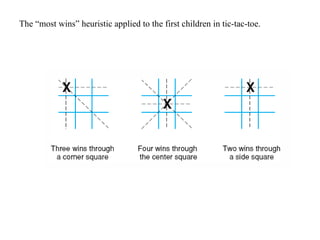
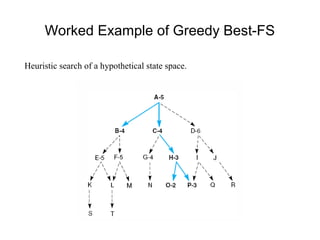
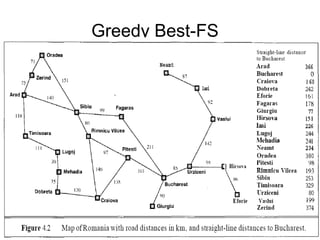
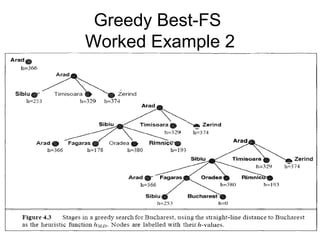
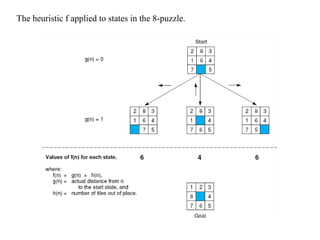
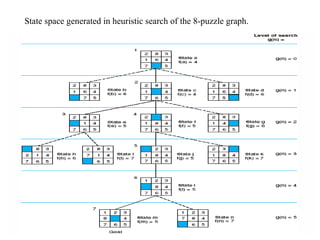
Heuristics are rules used in informed search algorithms to efficiently navigate state spaces toward solutions, especially when exact solutions are infeasible or too costly to compute. Various heuristic methodologies exist, including hill climbing and best-first search, each with its own advantages and limitations, such as the tendency of hill climbing to get stuck in local maxima. The A* search algorithm improves heuristic evaluation by combining the actual path length with an admissible heuristic estimate to better guide the search toward optimal solutions.

1. Informed search algorithms
Lecture 4

2. Introduction
• Heuristics are formalized as rules for choosing
those branches in a state space that are most
likely to lead to an acceptable problem solution.
• Much more efficient than un-informed searches.
• Heuristics are employed in two basic situations:
– A problem may not have an exact solution because of
inherent ambiguities in the problem statement or
available data
– A problem may have an exact solution, but the
computational cost of finding it may be prohibitive

3. Limitations
• Heuristics are fallible
• Only an informed guess of the next step to
be taken in solving a problem
• Based on limited information
• Often based on experience or intuition
• Heuristic algorithm has two parts
– The heuristic measurement
– An algorithm that uses it to search the state
space (best first search)

4. The “most wins” heuristic applied to the first children in tic-tac-toe.

5. Hill Climbing Search
• The simplest way to implement a heuristic search
• Like climbing the Mount Everest in thick fog with
amnesia
• Hill climbing strategies expand the current state in
the search and evaluate its children
• The best child is selected for further expansion;
neither its parent nor its siblings are retained
• Search halts when it reaches a state that is better
than any of its children

6. Hill-climbing search

7. Limitations of Hill Climbing Search
• Because it keeps no history, the algorithm
cannot recover from failure of its strategy
• Tendency to become stuck in local
maxima

8. Hill-climbing search Example

9. BEST FIRST SEARCH (BEST-FS)

10. Variants of BEST-FS
• Greedy BEST-FS
– Only the heuristic value is considered
– The path cost is not considered
• Beam Search
– Operates in a level-by-level manner
– Searches at most m children of the nodes
expanded at the previous level
– Selects the best m children according to some
heuristic evaluation

11. Heuristic search of a hypothetical state space.
Worked Example of Greedy Best-FS

12. A trace of the execution of Greedy Best_FS for the example

13. Greedy Best-FS

14. Greedy Best-FS
Worked Example 2

15. Greedy Best-FS is not optimal-
Example
h(n1)=200h(n1)=200 h(n3)=50h(n3)=50
100100
100100
1010
1010
1010

16. Implementing heuristic evaluation
functions (A* Search)
• Because heuristics are fallible, it is
possible that a search algorithm can be
misled down some path that fails to lead to
a goal
• If two states have approximately the same
heuristic value, examine the state that is
nearest to the root of the state graph.
• This state will have a greater chance of
being on the shortest path to the goal

17. • this makes our evaluation function, f, the
sum of two components
f(n)=g(n)+h(n)
• where g(n) measures the actual length of
the path from any state n to the start state.
• h(n) is an admissible heuristic estimate of
the distance from state n to a goal
A* Search

18. The heuristic f applied to states in the 8-puzzle.

19. State space generated in heuristic search of the 8-puzzle graph.

20. The successive stages of open and closed that generate this graph are: