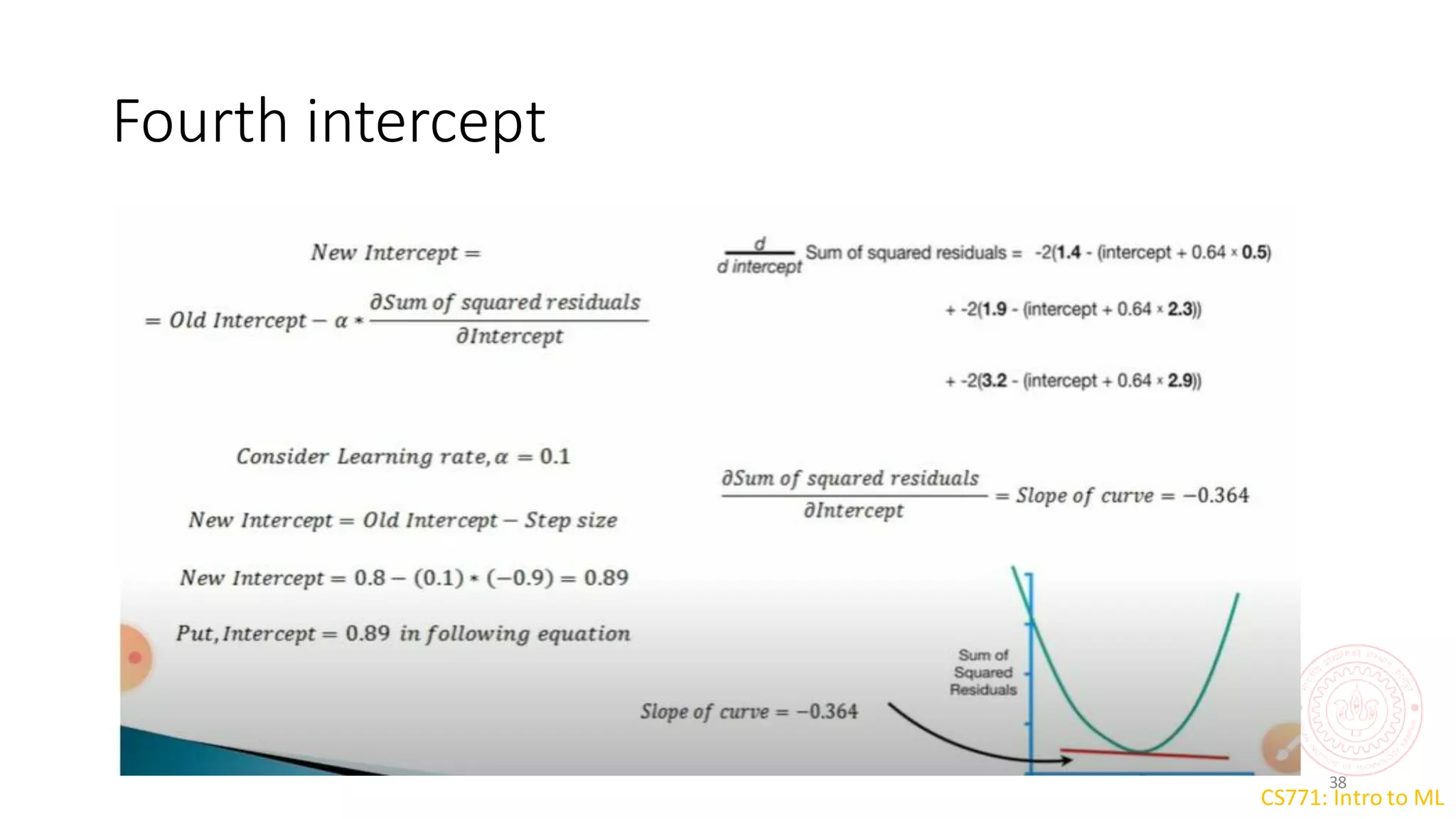
The document discusses the gradient descent algorithm, which is an optimization technique used to minimize loss functions in machine learning models. It works by iteratively taking steps in the direction of steepest descent from the objective function. The learning rate determines step size, with higher rates covering more ground but risking overshooting the minimum. Gradient descent is used to update a model's parameters, like coefficients in linear regression, to reduce loss.