This document discusses properties and generation of graceful graphs and trees through graceful codes. Some key points: - Graceful codes represent graceful graphs through sequences of integers that satisfy certain properties. α-valuable codes and gracious codes are types of graceful codes. - Properties of graceful/α-valuable codes are discussed, such as how codes can be combined or modified to generate new codes representing larger graphs. - Theorems show how α-valuable codes of trees can be used to generate codes for larger trees through operations like duplication, insertion, or concatenation of codes. This provides an algorithmic way to systematically generate infinite families of graceful tree codes.

1. 26VIT
1984-2010
Creating Stars

2. 26VIT
1984-2010
Creating Stars
A Place to Learn ; A Chance To Grow

3. 26VIT
1984-2010
Creating Stars
ncmowli@hotmail.com
N.Chandramowliswaran
Applied Algebra Division
School of Advanced Sciences
VIT University
26VIT
1984-2010
Creating Stars
ncmowli@hotmail.com
Claude Berge Bill Tutte
Generation of Graceful Trees through
Graceful Codes

4. Abstract
Graceful Code is a way to represent graceful graph in terms
of sequence of non-negative integers. Given a graceful
graph G on “q” edges, we can generate its graceful code in
the form of (a1, a2, a3, …., aq-1, aq=0) to represent the
graph. Similarly, we can easily draw the graph from the
given graceful code.
Graceful codes are classified into two categories, namely,
α-valuable code and gracious code based on their
properties. Graceful code provides an useful and efficient
techniques to study and analyze graphs using computer.
Here we discuss generation of infinitely many graceful
codes, α-valuable codes and gracious codes for a given
graceful code, α-valuable code and a gracious code.

5. Introduction
A simple graph G(V,E) on “p” vertices and “q”
edges is said to be graceful if there exist
an injection f: V→{0, 1, 2,….,q} such that the
induced function g: E→{1, 2, 3, …, q} which is
defined by g(u, v)=|f(u)-f(v)| for every edge
(u, v), is a bijective function; then “f” is called
graceful labelling of G.

6. Graceful Code
Let G be any graceful graph on “q” edges then
(a1, a2, a3, …, aq -1, aq) is called a graceful code of G,
if 0 ≤ ai ≤ q - i; 1 ≤ i ≤ q.
Here ai is the lower end vertex of the edge label “i”.
It is important to note that aq is always zero
 For every graceful graph G we can write its code.
Conversely, for every given graceful code we can draw
the corresponding graceful graph as follows.
Join edges:(a1,1+a1),(a2,2+a2),...,(aq - 1,q-1+aq-1), (aq, q+aq)

7. Example 1
Figure 1 shows a graceful graph on q = 7 edges
with edge labeled from 1 to 7.
7
0
6
3
12
4
5
Code = (4, 2, 3, 0, 1, 0, 0)
Figure 1

8. - valuable Code
A graceful code (a1, a2, a3,..., aq-1, aq) of a
graceful graph G on “q” edges is called
α - valuable code if
Here a1 is called the separator or critical value
of the - valuable code.
a1  ai
Max{ai| 1≤ i ≤ q} < Min{i+ai| 1≤ i ≤ q}.

9. Proposition
(a1, a2, a3, …,aq-1,aq) represents -valuable code if
and only if
0  (a1 – aq - i + 1) / q – i) ≤ 1
for all i , 1 ≤ i ≤ q - 1
 Equivalently (a1, a2, a3, …,aq-1,aq) represents an
- valuable code if and only if
(a1 - aq, a1 - aq -1, …, a1 - a3, a1 - a2, 0) represents a
code of a Graceful Graph.

10. Properties of Graceful Codes
1.1 If (a1, a2, a3,…, aq - 1, aq) represents a code of
a graceful graph G on “q” edges,
then, (a2, a3,…, aq - 1, aq) represents a code
of some graceful graph H on “q - 1” edges.
1.2 If (a1, a2, a3,…, aq-1, aq) is an α–valuable
code on “q” edges and (q -1 - a1 > a1)
then (q – 1 - a1, q – 2 - a2, …, 1- aq - 1, 0,
a1, a2,a3,…, aq) is an α–valuable code
on “2q” edges.

11. 1.3. If (a1, a2, a3,…, aq - 1, aq) is an α–valuable
code on “q” edges and (a1> q -1 - a1) then,
(a1, a2, a3,…, aq, q - 1- a1, q – 2 - a2, …,1 – aq - 1, 0)
is an α–valuable code on “2q” edges.
1.4. If (a1, a2, a3,…, aq1 - 1, aq1) and
(b1, b2, b3, …, bq2 - 1, bq2) represents
α–valuable codes on “q1” and “q2” edges
respectively and a1 ≥ b1 then,
(a1, a2, a3,…, aq1 - 1, aq1, b1, b2, b3,…, bq2 - 1, bq2)
represents an α–valuable code
on “q1 + q2” edges.

12. 1.5. Let (a1, a2, a3,…, aq -1, aq) represents
a graceful code of a graph G on
“q” edges then,
(aq+ q, aq - 1+ q - 1,…, 2 + a2, 1 + a1, a1, a2, a3,…, aq - 1, aq)
represents a α–valuable code on “2q” edges.

13. Properties of Graceful Codes
 If (a1, a2, a3,…, aq - 1, aq) represents a graceful
code of a graceful graph G on “q” edges then,
(aq+ q, aq – 1 + q - 1,…,2 + a2, 1 + a1, x, a1, a2, a3…, aq - 1, aq),
[0 ≤ x ≤ q] represents an α–valuable code
on “2q + 1” edges.

14. If (a1, a2, …, aq  1, aq) represent a code of a
graceful graph G on q edges,
Then,
(q – aq, q – aq  1, …, q – a2, q – a1, a1, a2, …, aq  1, aq)
represent a  -valuable code on “2 q” edges.

15. Properties of Graceful Codes
Let X1, X2, X3, …, Xr represent “r” α–valuable
codes on edges “qi”
(1 i  r) having separators “si” respectively.
Then,
r-1 r-2 r-3
(  sj + Xr ,  sj + Xr-1 ,  sj + Xr-2 , … s1+ s2+ X3, s1+ X2, X1)
j=1 j=1 j=1
r
always represent a α–valuable code on  qj edges.
j = 1

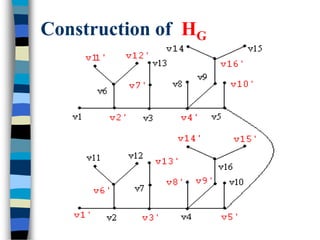
16. Tree Generation Theorems
Let G be any simple graph on “n” vertices and “q”
edges.
Define a bipartite graph HG as follows:
(vi, vj)  E(G) <=> (vi, vj’)  E(HG) and
(vi’, vj)  E(HG).
Join any vk  V(G)  V(HG),
[1 ≤ k ≤ n] to vk’  V(HG).
Here |V(HG)| = 2|V(G)| and |E(HG)| = 2 | E(G)| +1.

17. Tree Generation Theorems
Moreover if G has a code (a1, a2, a3,…, aq - 1, aq)
then HG has an α–valuable code
(aq+ q, aq-1+q - 1,…, 2+a2, 1 + a1, x, a1, a2, a3, …, aq - 1, aq)
[0 ≤ x ≤ q].
If G happens to be a bipartite graph, then HG
contains two copies of G
together with an edge connecting vk to vk’

18. Examples
Code = (0, 1, 0, 0)
G
HG
Code = (4, 3, 3, 1, 3, 0, 1, 0, 0)

19. Examples
G

20. Construction of HG

21. ai i + ai
i
E (G)

ai i + ai
q+1+ai q+1+i+ai
E(HG)
q+1+i
q+1-i
(aq+q, …,ai+i, …,1+a1, x, a1, …, ai, …, aq)
q+1+ai q+1+i+ai
q+1-i q+1+i
i i

22. Tree Generation Theorems
Theorem
If (a1, a2, a3,…, aq -1, aq) represents a α–valuable
code of some tree “T” . Then,
(aq+q, aq - 1+q-1, …,2+a2, 1+a1, a1, a2, a3,…, aq - 1, aq)
represents a α–valuable code of a tree “S”
on “2q” edges such that
E(S) = E(T) U E(T).

23. Tree Generation Theorems
Theorem
If (a1, a2, a3,…, aq-1, aq) is an α–valuable code of a
graceful graph G on “q” edges, then,
(a1, a2, a3,…, aq-1, aq) represents a tree if and only if
(a2, a3,…, aq -1, aq) represents a tree
on “q - 1” edges.

24. Tree Generation Theorems
If (a1, a2, …, aq-2, aq-1, aq ) represents a code of a
graceful tree on ‘q’ edges, then
1. (qk - 1, ka1, (q –1) k –1, ka2, …, 2 k - 1, kaq - 1, 1k - 1, kaq)
represent a tree code on “kq” edges (k  2).
2. (qk - 1, ka1+r, (q –1) k – 1, ka2+r, …, 2k - 1, kaq-1+r, 1k - 1,
kaq+r, 0r) ;1 ≤ r ≤ k, k ≥ 2 represent a tree code
on “kq+r” edges.

25. Corollary – 1
If (a1, a2, …, aq - 2, aq - 1, aq ) represents a code of a
graceful tree on ‘q’ edges, then
(q, 2a1, q - 1, 2a2, q - 2, 2a3, …, 2, 2aq - 1, 1, 2aq)
represent a code of a graceful tree on “2q” edges and
(q, 2a1+1, q - 1, 2a2+1, q - 2, 2a3+1, …, 2, 2aq - 1+1, 1,
2aq+1,0) represent a tree code on “2q+1” edges.

26. Corollary – 2
If (a1, a2, …, aq-2, aq-1, aq ) represents a code of a
graceful tree on ‘q’ edges, then
(q+1, 2a1, q, 2a2, q - 1, 2a3, …, 3, 2aq-1, 2, 2aq, 1, 0)
represent a code of a graceful tree on “
2q+2” edges and (q+1, 2a1+1, q, 2a2+1, q - 1,
2a3+1, …, 3, 2aq - 1+1, 2, 2aq+1, 1, 0, 0)
represent a tree code on “2q + 3” edges.

27. Tree Generation Theorems
Using - valuable tree codes
Theorem 1
If (a1, a2, …, aq - 1, aq) represent a -valuable tree
code on “q” edges, then,
(aq+q, aq - 1+ q – 1, …, 2 + a2, 1+ a1, 1 + a1, a1, a1,a2,
…, aq - 1, aq)
represent a -valuable tree code on “2q+2” edges.

28. Theorem 2
Let (a1, a2, …, aq1 - 2, aq1 - 1, aq1) represents a
 - valuable tree code on “q1” edges and
(b1, b2, …, bq2 - 2, bq2 - 1, bq2) represent a tree code on
“q2” edges. Then,
1. (a1 + b1 , a1 + b2, …, a1 + bq2 - 2, a1+ bq2 - 1, a1+ bq2,
a1, a2, …, aq1 - 2, aq1 - 1, aq1 ) represent a tree code
on “q1 + q2” edges.

29. Tree Generation Theorems Using
- valuable tree codes
2. (a1+ b1, a1+b2, …, a1+ bq2 - 2, a1+bq2 - 1, a1+bq2, a1
– aq1, a1 – aq1 - 1,a1 aq1 - 2, …, a1 – a2, 0)
represent a tree code on “q1+ q2” edges.
3. (q1– 1 – a1 + b1, q1– 1 – a1+ b2, q1– 1 – a1+ b3,
…, q1– 1– a1+ bq2 - 2, q1– 1– a1+ bq2 - 1, q1– 1 –
a1+ bq2, q1– 1– a1, q1 – 2 – a2, …, 2  aq1 - 2, 1 
aq1 - 1, 0) represent a tree code on “q1+ q2”
edges.

30. Tree Generation Theorems Using
- valuable tree codes
4. (q1– 1 – a1+ b1, q1– 1 – a1+ b2, q1– 1 – a1+ b3 ,
…, q1– 1 – a1+ bq2 - 2, q1– 1 – a1+ bq2 - 1, q1– 1 –
a1+ bq2, q1– 1 – a1, q1– 2 – (a1  aq1 - 1),
q1 – 3 – (a1  aq1 - 2), …, 1 – (a1 – a2), 0)
represent a tree code on “q1+ q2” edges.
5. (a1+ a2, a1+ a3, a1+ a4, …, a1+ aq1 - 2, a1+ aq1 - 1,
a1+ aq1, a1, a2, …, aq1 - 2, aq1-1, aq1) represent a
tree code on “2q – 1” edges.

31. Tree Generation Theorems Using
- valuable tree codes
Corollary 1
Let X1, X2, X3, …, Xr represent “r” α–valuable tree
codes on edges “qi”
(1 i  r) having separators “si” respectively.
Then
r- 1 r- 2 r- 3
(  sj + Xr,  sj + Xr - 1,  sj + Xr - 2, …, s1+ s2+ X3, s1+ X2, X1)
j=1 j=1 j=1
r
always represent a α–valuable tree code on  qj edges.
j=1