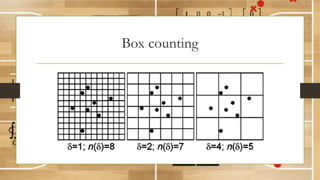
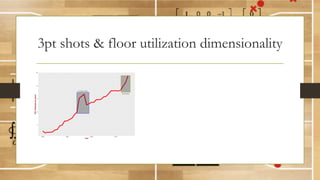
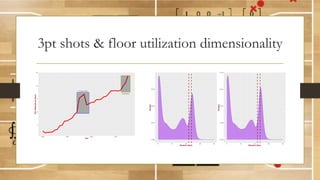
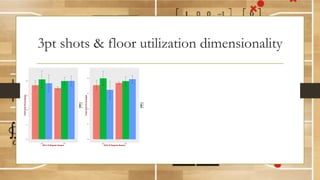
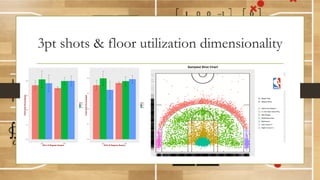
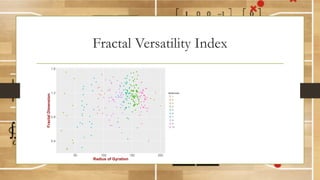
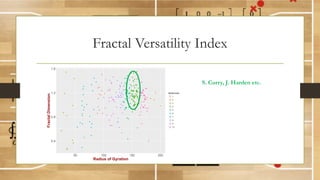
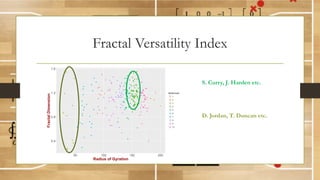
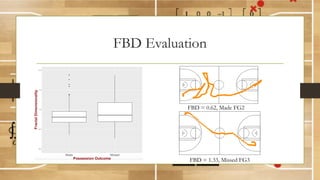
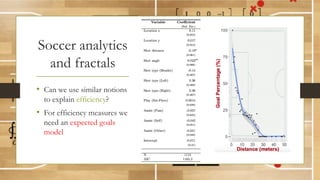
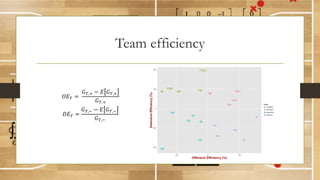
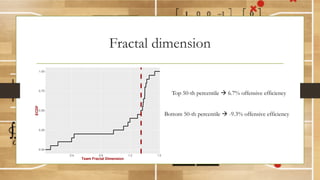
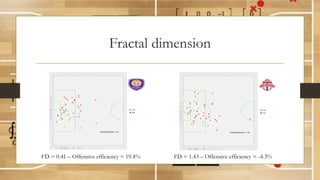
This document discusses using fractal analysis to analyze sports data. It provides examples of calculating fractal dimensions of dancing styles, shot charts in basketball, and soccer team efficiency. Calculating the fractal dimension can provide a single number to describe complex spatial patterns and quantify concepts like versatility. For example, shot charts with higher fractal dimensions indicate more varied shooting locations. This type of analysis may provide new insights into player/team performance beyond traditional statistics.

1. Sports and Fractals
Konstantinos Pelechrinis
@kpelechrinis

2. Sports …

3. …and fractals?

4. …and fractals?

5. Self similarity
• A self similar complex system or object exhibits the same statistical
properties over different scales
• Scale invariance à ∃Δ: f λx = 𝜆) 𝑓 𝑥 , ∀𝜆
Power laws
K. J. Hsu and A. Hsu, “Self-similarity of the “1/f noise” called music”,
in PNAS, vol 88, pp 3507-3509, April 1991
Coastline paradox

6. Why sports though?
• Several spatial sports data
• Player mobility, shot charts etc.
• The complexity of similar objects can be captured through the notion of
fractal dimensionality
With C(r) being the fraction of pairs of points from a set S that have distance smaller or equal to r,
S behaves like a fractal with intrinsic fractal dimension D in the range of scales r1 to r2, iff:
𝐶 𝑟 ∝ 𝑟1
, 𝑟2 ≤ 𝑟 ≤ 𝑟4

7. Fractal dimension
Fractal dimension = 0.48 Fractal dimension = 1.61 Fractal dimension = 1.94

8. Box counting

9. Fractal dimensionality and … dancing
Dance Fractal dimensionality
Rumba 1.36
Cha cha 1.24
Salsa 1.28
Merengue 1.16
Bachata 1.21
Salsa
Merengue
M. Tatlier and R. Suvak, “How fractal is dancing?”, Chaos, Solitons and Fractals 36 (2008) 1019-1027

10. Fractal dimensionality and … dancing
Dance Fractal dimensionality
Rumba 1.36
Cha cha 1.24
Salsa 1.28
Merengue 1.16
Bachata 1.21
Salsa
Merengue
M. Tatlier and R. Suvak, “How fractal is dancing?”, Chaos, Solitons and Fractals 36 (2008) 1019-1027

12. 3pt shots & floor utilization dimensionality
3PT distance changes
Record breaking
5
10
15
20
25
1980 1990 2000 2010
Year
3PTAttemptsperGame

13. 3pt shots & floor utilization dimensionality
3PT distance changes
Record breaking
5
10
15
20
25
1980 1990 2000 2010
Year
3PTAttemptsperGame
0.000
0.025
0.050
0.075
0 10 20 30 40
Distance (feet)
Density
0.000
0.025
0.050
0.075
0 10 20 30 40
Distance (feet)
Density
0.000
0.025
0.050
0.075
0.100
0 10 20 30 40
Distance (feet)
Density
0.000
0.025
0.050
0.075
0 10 20 30 40
Distance (feet)
Density
0.000
0.025
0.050
0.075
0.100
0 10 20 30 40
Distance (feet)
Density

14. 3pt shots & floor utilization dimensionality
3PT distance changes
Record breaking
5
10
15
20
25
1980 1990 2000 2010
Year
3PTAttemptsperGame
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2015-16 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2014-15 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2014-15 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2014-15 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2015-16 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right

15. 3pt shots & floor utilization dimensionality
3PT distance changes
Record breaking
5
10
15
20
25
1980 1990 2000 2010
Year
3PTAttemptsperGame
0.000
0.025
0.050
0.075
0 10 20 30 40
Distance (feet)
Density
0.000
0.025
0.050
0.075
0 10 20 30 40
Distance (feet)
Density
0.000
0.025
0.050
0.075
0.100
0 10 20 30 40
Distance (feet)
Density
0.000
0.025
0.050
0.075
0 10 20 30 40
Distance (feet)
Density
0.000
0.025
0.050
0.075
0.100
0 10 20 30 40
Distance (feet)
Density
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2015-16 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2014-15 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2014-15 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2014-15 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
0.0
0.1
0.2
0.3
0.4
2PT 3PT
2015-16 Regular Season
FieldGoalPercentages
Position
Crest
Left
Right
Made Shot
Missed Shot
Above the Break 3
In The Paint (Non-RA)
Mid-Range
Restricted Area
Backcourt
Left Corner 3
Right Corner 3
Sampled Shot Chart

16. Floor utilization dimensionality
Isn’t this something we already know?!?!
Yes, but this shows that fractal dimensionality can be useful

17. Fractal versatility index
• Objective: quantify the spatial distribution of a player’s shot choices
• Proxy for versatility
Made Shot
Missed Shot
2014-15 Shot Chart
Giannis Antetokounmpo
NDSL@Pitt
FD = 0.72

18. Shot chart fractal dimensionality
1.42 1.38 1.11 0.96
0.57 0.31 1.27 1.44

19. Shot chart fractal dimensionality
1.42 1.38 1.11 0.96
0.57 0.31 1.27 1.44

20. Shot chart fractal dimensionality
1.42 1.38 1.11 0.96
0.57 0.31 1.27 1.44

21. Radius of gyration
140.6 166.3 140.7 125.6
25.4 36.2 113.2 83.2

22. Fractal Versatility Index
0.4
0.8
1.2
1.6
50 100 150 200
Radius of Gyration
FractalDimension
factor(clus)
1
2
3
4
5
6
7
8
9
10

23. Fractal Versatility Index
0.4
0.8
1.2
1.6
50 100 150 200
Radius of Gyration
FractalDimension
factor(clus)
1
2
3
4
5
6
7
8
9
10
S. Curry, J. Harden etc.

24. Fractal Versatility Index
0.4
0.8
1.2
1.6
50 100 150 200
Radius of Gyration
FractalDimension
factor(clus)
1
2
3
4
5
6
7
8
9
10
S. Curry, J. Harden etc.
D. Jordan, T. Duncan etc.

25. Fractal dimension and ball movement
• Fractal dimensionality of the ball’s trajectory is an one number description of ball
movement
• Ball movement can be intuitively thought of as a self-similar process
• Evaluation? Possibly manual but time-consuming
• Indirect evaluation: good ball movement should produce successful possessions

26. FBD Evaluation
• Logistic regression with DV the success (made FG) or not (missed FG, TO)
of a possession and FBD of the possession as the only IV

27. FBD Evaluation
FBD = 0.62, Made FG2
FBD = 1.33, Missed FG3

28. Soccer analytics
and fractals
• Can we use similar notions
to explain efficiency?
• For efficiency measures we
need an expected goals
model

29. Team efficiency
𝑂𝐸7 =
𝐺7,: − 𝐸 𝐺7,:
𝐺7,:
𝐷𝐸7 =
𝐺7,= − 𝐸 𝐺7,=
𝐺7,=
CHI
CO
COL
DAL
DC
HOU
LA
MTL
NE
NYCFC
NYRB
OCSC
PHI
POR
RSL
SEA
SJ
SKC
TOR
VAN
-60
-30
0
30
60
-20 0 20
Offensive Efficiency (%)
DefensiveEfficiency(%)
Teams
a
a
a
a
Complete
Defensive
Need Work
Offensive

30. Fractal dimension
0.00
0.25
0.50
0.75
1.00
0.4 0.8 1.2 1.6
Team Fractal Dimension
ECDF
Top 50-th percentile à 6.7% offensive efficiency
Bottom 50-th percentile à -9.3% offensive efficiency

31. Fractal dimension
Fractal Dimension = 0.4
Goal
Miss
Fractal Dimension = 1.42
Goal
Miss
FD = 0.41 – Offensive efficiency = 19.4% FD = 1.43 – Offensive efficiency = -4.3%

32. More possibilities
• SportVU data
• PITCHf/x data
• Pitcher’s fractal dimension (?)
• Can it provide any new knowledge that we do not know already ?
• NextGen NFL stats
• Fractal dimension of successfully run routes (?)

33. Sources
• Perl code:
http://www.cs.cmu.edu/afs/cs.cmu.edu/user/christos/www/SRC/FracDim
-20001026.tar.gz
• R package: https://cran.r-
project.org/web/packages/fractaldim/fractaldim.pdf
• Matlab: https://www.mathworks.com/matlabcentral/fileexchange/13063-
boxcount