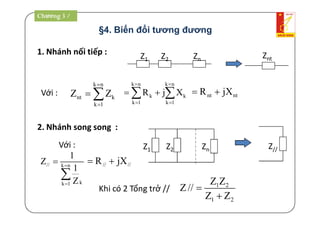
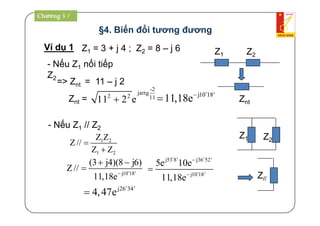
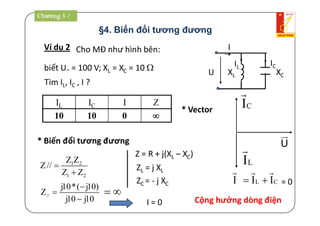
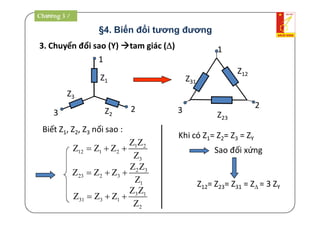
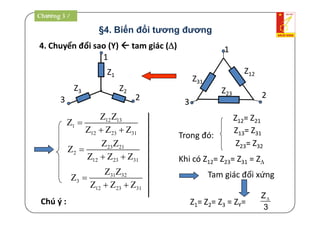
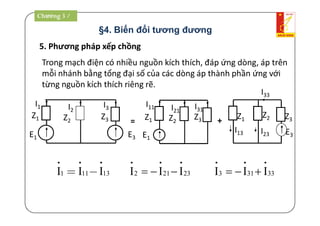
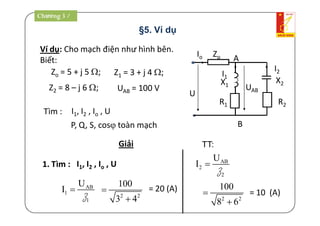
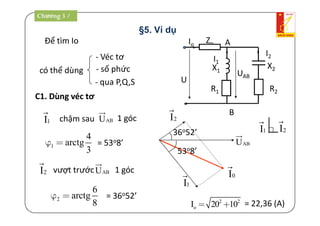
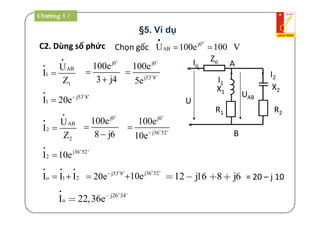
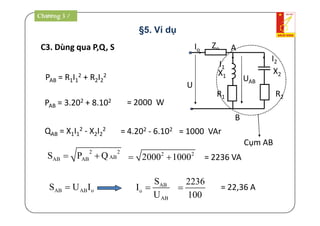
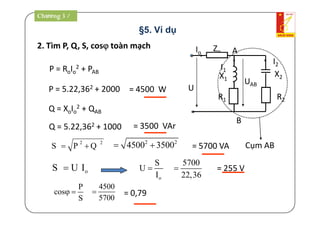
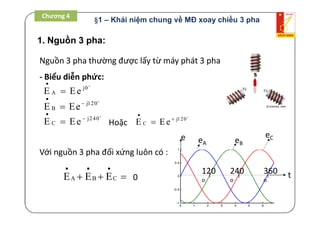
Tài liệu là giáo trình về thiết bị điện - điện tử trong kỹ thuật điện, bao gồm nội dung lý thuyết và thực hành liên quan đến mạch điện và máy điện. Nó trình bày các khái niệm cơ bản, các phương pháp giải mạch điện, và công suất trong mạch xoay chiều, cùng với các định luật cơ bản. Tài liệu cũng gồm hướng dẫn bài tập và điều kiện thi cho sinh viên.

1. Bộ môn: THIẾT BỊ ĐIỆN - ĐIỆN TỬ
KỸ THUẬT ĐIỆN

2.  Bộ môn: THIẾT BỊ ĐIỆN - ĐIỆN TỬ
 VP: C3 – 106 Tel. 04 3869 2511
 Giảng viên: Ngô Văn Quyền
 email: quyennv-fee@mail.hut.edu.vn
Tài liệu học tập
Đặng Văn Đào, Lê Văn Doanh, Kỹ thuật điện, NXB KHKT 2002.
Phan Thị Huệ, Bài tập Kỹ thuật điện - trắc nghiệm và tự luận, NXB
Lao động và xã hội, 2004, NXB KHKT, 2008
Liên hệ và tài liệuLiên hệ và tài liệu

3. Khối lượng: 3
o Lý thuyết 40 tiết
o Bài tập:
o Thí nghiệm:
Đánh giá kết quả
o Thi cuối kỳ (trắc nghiệm): trọng số 0,7
o Điều kiện dự thi cuối kỳ: dự đủ 75% giờ giảng
Khối lượngKhối lượng

4. NỘI DUNG
PHẦN I. MẠCH ĐIỆN
Chương 2. Dòng điện hình sin
Chương 3. Các phương pháp giải mạch điện
Chương 4. Mạch điện 3 pha
Chương 1. Những khái niệm cơ bản về mạch điện

5. NỘI DUNG
PHẦN II. MÁY ĐIỆN
Chương 6. Máy biến áp
Chương 7. Máy điện không đồng bộ
Chương 8. Máy điện đồng bộ
Chương 9. Máy điện một chiều
Chương 5. Khái niệm chung về máy điện

6. PHẦN I. MẠCH ĐIỆN
Chương 1. Những khái niệm cơ bản về mạch điện
số vòng độc lập
2. Kết cấu :
§1 - Mạch điện và kết cấu của mạch điện
1. Định nghĩa:
a- Nhánh
b- Nút :
c- Vòng :
nguồn
tải
MF ĐC
b.đèn Cuộn dây Tụ
i1
i4
i5
i3i2
(5)
(4)
(2)
A
B

7. §2. Các đại lượng đặc trưng cho QTNL trong MĐ
Dòng điện :
Ký hiệu:
i, I
Đơn vị
A, mA, kA...
Điện áp u, U V, mV, kV
o Chiều của dòng điện và điện áp: 1 2
1 : Điện thế tại điểm 1
2 : Điện thế tại điểm 2
Nếu 1 > 2 thì chiều của điện áp u12 có chiều từ 1  2
Chiều của điện áp và dòng điện thường không biết trước
Giả thiết chiều của dòng điện và điện áp
a/ Điện áp và Dòng điện :
u12
Chương 1 /

8. §2. Các đại lượng đặc trưng cho QTNL trong MĐ
VA, kVA
i i
e e
u u
R R
a b
phát NL
b/ Công suất
• Công suất tác dụng P W, kW
• Công suất tức thời p
Khi u, i cùng
chiều qui
ước (a)
p >0 nhận NL
p < 0
• Công suất phản kháng Q VAr, kVAr
• Công suất toàn phần S
= ui
Chương 1 /

9. §3. Các phần tử lý tưởng đặc trưng cho mạch điện
lý tưởng
thực tế
ue
Rtr
e u
1. Nguồn điện áp ( nguồn S.Đ.Đ)
Nguồn điện áp lý tưởng :
u = e
Nguồn thực tế :
u = e – Rtr i
u = -e
e u
i
tải
i
tải
u
i
0
u
Chương 1 /

10. §3. Các phần tử lý tưởng đặc trưng cho mạch điện
2. Điện trở:
Điện áp : uR = Ri
Công suất : p = uRi= Ri2
i
uR
R
Chương 1 /
L
uL
iL
i~
uL = - eL
L
L
di
u L
dt

3. Điện cảm
= WΨ(i)
số vòng
dây
C
Cu 
4. Điện dung :
uCuC~
iC
C
1
i dt
C q~

11. §4. Sơ đồ thay thế ( Mô hình mạch điện)
R C
Rđ/c
L
Lđ/c
i3i2 i4
i5i1
MF ĐC
b.đèn Cuộn dây Tụ
A
B
i1
i4
i5
i3i2
ue
Rtr
RL
Chương 1 /

12. §5. Hai định luật cơ bản
Chương 1
1- Định luật Kiechop 1( K1) :
k n
k
k 1
i 0



i1 – i2 –i3 –i4 –i5 = 0
u Le R C
Rđ/c
Lđ/c
i3i2 i4
i5i1 A
B
tại A:
tại B: - i1 + i2 +i3 +i4 +i5 = 0
n-1 PTĐLn nút:
- Phát biểu cho
dòng điện tại các
nút
- Quy ước
dấu:
Dòng có chiều đi vào nút lấy dấu dương (+)
Dòng có chiều đi ra khỏi nút lấy dấu (-)
Chương 1 /

13. §5. Hai định luật cơ bản
Chương 1
2- Định luật Kiechop 2( K2) :
1 2k n k n
k k
k 1 k 1
u e
 
 
 
- Phát biểu cho điện áp trong các mạch vòng khép kín.
Chương 1 /
Qui trình viết:
 Chọn chiều của điện áp
 Chọn chiều của mạch vòng
 Viết biểu thức
Nếu điện áp (sdd) cùng chiều vòng ta lấy dấu dương (+)
và ngược lại
433
2
1
1
eedti
Cdt
di
LRi  
L
e3
R
C
i2i1
i3
A B
C
e4
ur
uL
uc

14. PHẦN I. MẠCH ĐIỆN
§1 – Các đại lượng đặc trưng cho dòng hình sin1
§ 2 – Biểu diễn dòng hình sin2
§ 3 – Định luật Kichop dạng vector / phức3
§ 4 – Dòng điện hình sin trong các nhánh cơ bản4
Chương 2. Dòng điện xoay chiều hình sin
§ 5– Công suất trong mạch hình sin5
§ 6 – Phương pháp nâng cao hệ số công suất cos6

15. Chương 2. Dòng điện xoay chiều hình sin
§1 – Các đại lượng đặc trưng cho dòng hình sin
0 1 2 3 4 5 6 7
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
t
i
m ii I sin( t )   
m uu U sin( t )   
m ee E sin( t )   
T
i
mI
1
f
T

it  
2 f  
Góc pha
 = 2f
Với u ,i là góc pha đầu f = 50Hz
ĐL đặc trưng:
Giá trị hiệu dụng
Góc pha đầu
Giá trị hiệu dụng
2
mU
U 
2
mI
I 

16. §1 - Các đại lượng đặc trưng cho dòng hình sin
u, i
Um
Im
u i

 
 o
o
ti
tu
60sin212
30sin2220







 o
u
30
220




 o
i
60
12
Ví dụ:
Góc lệch pha:
iu  
ooo
iu 90)60(30  
Bản chất các phần tử
Kết cấu của mạch
Chương 2 /

17. §2. Biểu diễn dòng hình sin
Chương 2 /
x0
A
A A
1. Bằng vector
Cho 1 vector:
A 


A
A
ψ
1 dòng hình sin:
i



i
I
ψ
Nếu coi: IA  iA   iA 
VD: Cho 1 nút mạch: i1, i2, i3
i1
i2
i3
 
 o
o
ti
ti
60sin26
30sin28
2
1




Tìm i3
321 iii  321 III  1I
1
2I
2
3I
3
AI 1068 22
3 
...60
2
10
3 
I
I
arctg
 Tiện cho việc cộng, trừ các dòng điện, điện
áp cùng tần số
Chương 2 /

18. §2. Biểu diễn dòng hình sin
2. Bằng số phức
a, b : số thực
Dạng đại số :
Dạng lũy thừa :
số ảo1-j 
jba 
o
A jba 
o
A
A
j
AeA A

 .A
o
A
j
0 a
b 
A
o
A
A: modul
A: Argument
Cho dòng hình sin:
i



i
I
ψ
IA  iA   i
o
A
i
j
IeI i

 .I
o
VD:
 
 o
o
tu
ti
15sin2220
30sin2101




0o
0o
15
30
.220U
.10I
j
j
e
e

 
Chương 2 /

19. §3. Định luật Kichop dạng vector / phức
1. Quy ước
Tức thời: i , u , e
Hiệu dụng : I , U , E
Dạng Phức:
ooo
E,U,I
2. K1
0I
o
k 
3. K2
 
oo
EUk l
Chương 2 /

20. §4. Dòng điện hình sin trong các nhánh cơ bản
1. Nhánh thuần trở:
Cho : R
i uR
R Ri 2I sin t 
R2RI sin t 
R = ψu - ψi = 0
• Dạng véc tơ:
RI

RU

UR = RIR ψu = 0
=> uR = RiR
• Dạng phức :
RRU R I
 

uj
R RU U e



R RI ,U
 
RRI
R = ψu - ψi = 0
RI

ij
e 
Chương 2 /
CS tiêu tán TB :
T
R R
0
1
P p dt
T
 
R RU I 2
RRI 0 

21. §4. Dòng điện hình sin trong các nhánh cơ bản
2. Nhánh thuần cảm:
L = ψu - ψi = 90o
• Dạng véc tơ:
• Dạng SP : LU


iL L
uL
L Li 2I sin t  (1)
L
L
di
u L
dt
 (2)
L Lu 2 LI sin( t+90 )    (3)
LI

LU

L2 LI cos( t)   UL = XLIL
ψu = 90o
L LI ,U
 
LLjX I

XL
xL = L
Chương 2 /
T
L L
0
1
P p dt
T
  0
QL = XL IL
2
CS phản kháng
VAr, kVAr
ULIL = QL

22. §4. Dòng điện hình sin trong các nhánh cơ bản
Chương 2 /
3. Nhánh thuần dung:
• Dạng phức: CC CU jX I
 
 
CiC
uC
C Ci 2I sin t 
C C
1
u i dt
C
 
C C
1
u 2 I sin( t-90 )
C
 


 = ψu - ψi = -90o
• Dạng véc tơ:
CI

CU

C
1
2 I ( cos t)
C
  

UC = XCIC
ψu = -90o
Xc
Chương 2 /
T
C C
0
1
P p dt
T
  0
QC = -XC IC
2 VAr, kVAr
CS phản kháng
-UCIC = QC

23. §4. Dòng điện hình sin trong các nhánh cơ bản
4. Nhánh RLC nối tiếp:
I

i 2I sin t 
R L CU U U U  
   
RU

LU

CU

U

2 2
R L CU U +( U -U )
L C
R
U -U
arctg
U
 
uu 2U sin( t )   
= 
2 2
L CI R +( X -X )
X
L CX -X
arctg
R

X
arctg
R

u = uR + uL + uC
Lu
i
C
R
uC
uR
uL
 = u
Z
Z= I .
22
XR Z
Chương 2 /

24. §4. Dòng điện hình sin trong các nhánh cơ bản
Chương 2 /
4. Nhánh RLC nối tiếp:
- Khi XL > XC X > 0,  >0
U

vượt trước I

t/c điện cảm I

RU

LU

CU

U


- Khi XL < XC X < 0,  <0
U

chậm sau I

t/c điện dung
I

RU

LU

CU

U


- Khi XL = XC X = 0,  = 0
U

trùng pha I

cộng hưởng điện áp
I
RU

LU

CU

U

U

RU

=

25. §4. Dòng điện hình sin trong các nhánh cơ bản
4. Nhánh RLC nối tiếp:
Dạng phức:
Là tổng trở phức của nhánh
CLR UUUU



 IjXIjXIR CL ...   

 IXXjR CL .

 IZU .
jXRZ  j
e. Z
Tam giác tổng trở:

R
XZ
22
XR Z
R
CL
U
UU
arctg


R
XX
arctg CL 

R
X
arctg
cos/RZ sin/X
Chương 2 /

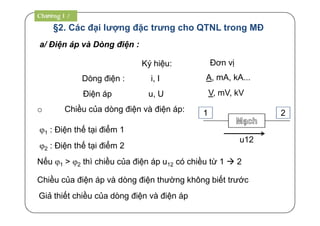
26. §5. Công suất trong mạch hình sin
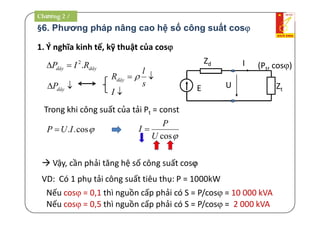
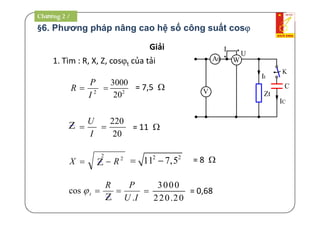
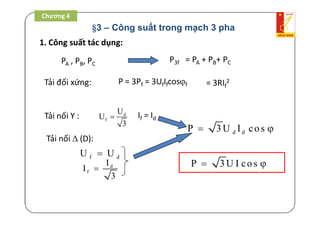
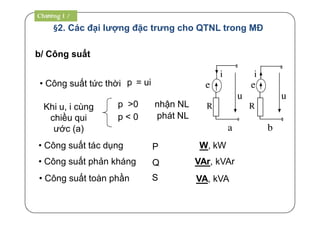
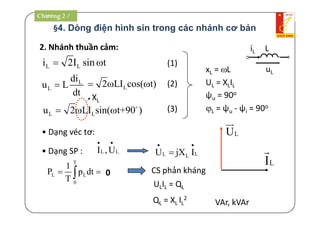
1. Công suất tác dụng P[W]:
RIP 2
 RI
U
.
Z
R
IU ..
Z
cos..IU
cos Gọi là hệ số công suất của mạch
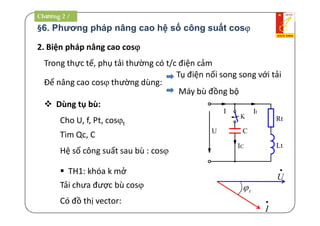
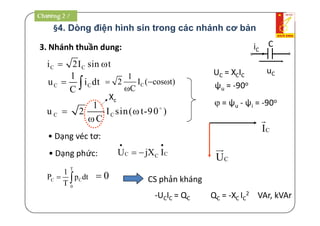
2. Công suất phản kháng Q[Var]:
 CL XXIQ  2
sin..IU
CL XIXIQ 22
 CL QQ 
LL XIQ 2

CC XIQ 2

Với:
Chương 2 /

27. §5. Công suất trong mạch hình sin
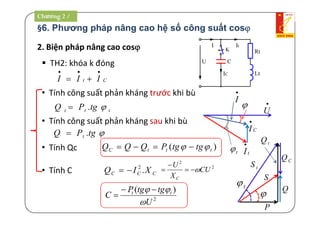
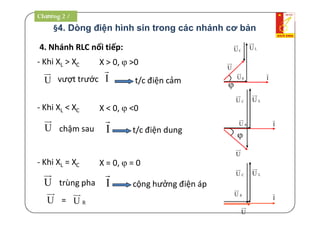
3/ Công suất toàn phần S[VA]:
22
QPS  IU.
Tam giác công suất: 
P
Q
PtgQ 
S
cos.SP  sin.SQ 
Công suất phức:



 IUS .
~ 

I : là dòng điện phức liên hợp
iu jj
IeUeS  
 .
~
j
eIU ..  sincos jUIUI 
jQPS 
~
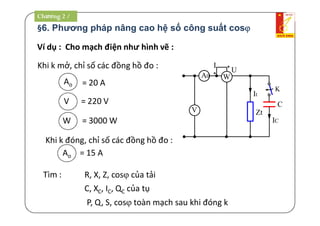
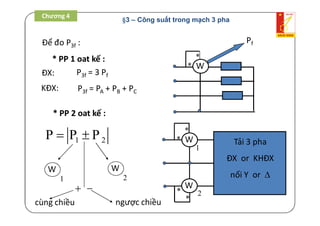
Đo công suất P:
UI
W1
*
*
U~
Z
Chương 2 /

28. §6. Phương pháp nâng cao hệ số công suất cos
1. Ý nghĩa kinh tế, kỹ thuật của cos
Zt
I
U
(Pt, cos)
Trong khi công suất của tải Pt = const
Zd
E
dâydây RIP .2

 dâyP

s
l
Rdây 
I
cos..IUP 
cosU
P
I 
 Vậy, cần phải tăng hệ số công suất cos
VD: Có 1 phụ tải công suất tiêu thụ: P = 1000kW
Nếu cos = 0,1 thì nguồn cấp phải có S = P/cos = 10 000 kVA
Nếu cos = 0,5 thì nguồn cấp phải có S = P/cos = 2 000 kVA
Chương 2 /

29. §6. Phương pháp nâng cao hệ số công suất cos
2. Biện pháp nâng cao cos
Trong thực tế, phụ tải thường có t/c điện cảm
Để nâng cao cos thường dùng:
Tụ điện nối song song với tải
Máy bù đồng bộ
 Dùng tụ bù:
U C
Rt
ItI
IC
K
Lt
 TH1: khóa k mở
Tải chưa được bù cos
Có đồ thị vector:

U
t
Cho U, f, Pt, cost
Tìm Qc, C

I
Hệ số công suất sau bù : cos
Chương 2 /

30. §6. Phương pháp nâng cao hệ số công suất cos
2. Biện pháp nâng cao cos
U C
Rt
ItI
IC
K
Lt
 TH2: khóa k đóng
Ct III


• Tính công suất phản kháng trước khi bù
ttt tgPQ .
• Tính công suất phản kháng sau khi bù
tgPQ t .
• Tính Qc )( tttC tgtgPQQQ  
• Tính C CCC XIQ .2
 2
2
CU
X
U
C



2
)(
U
tgtgP
C tt

 


U
tI

t

CI


I
t

CQ
tS
P
Q
S
tQ
Chương 2 /

31. §6. Phương pháp nâng cao hệ số công suất cos
Ví dụ : Cho mạch điện như hình vẽ :
Khi k mở, chỉ số các đồng hồ đo :
Ao = 20 A
V = 220 V
W = 3000 W
Khi k đóng, chỉ số các đồng hồ đo :
Ao = 15 A
P, Q, S, cos toàn mạch sau khi đóng k
Tìm : R, X, Z, cos của tải
C, XC, IC, QC của tụ
C
Zt
IC
K
W
*
*
U
I
It
V
A0
Chương 2 /

32. §6. Phương pháp nâng cao hệ số công suất cos
C
Zt
IC
K
W
*
*
U
I
It
V
A0
Giải
1. Tìm : R, X, Z, cost của tải
2
3000
20
 = 7,5 
= 11 
2 2
11 7,5  = 8 
3000
220.20
 = 0,68
20
220

2
2
RX 
Z
2
I
P
R 
I
U

Z
IU
PR
t
.
cos 
Z
Chương 2 /

33. §6. Phương pháp nâng cao hệ số công suất cos
P
U. I®
2. Tìm C, XC, IC, QC của tụ
tgt= 1,078
3000
220.15
 = 0,91
tg= 0,46 = 1,22.10-4 F
= 122 F
b 2
3000
C (1,078 0,46)
220 314
 
Xc =
1
C
4
1.10
314.1,22
 = 26,1 
IC =
C
U
X
220
26,1
 = 8,43 A
= - 1855 VAr
68,0cos t )(2 t
t
b tgtg
U
P
C 


cos
CCCC UIXIQ  2
)( tt tgtgP  
0,46)3000(1,078
Chương 2 /

34. §6. Phương pháp nâng cao hệ số công suất cos
3. Tìm P, Q, S, cos toàn mạch sau khi đóng k
P =
Q =
S =
Q  1380 VAr
3000 W
Qt + QC = Pttg1-1855 = 3000.1,078-1855
U.Iđ = 220.15 = 3300 VA
2cos  0,91
Q = Ptg2 = 3000.0,46
Chương 2 /

35. Bộ môn: THIẾT BỊ ĐIỆN - ĐIỆN TỬ
KỸ THUẬT ĐIỆN

36. PHẦN I. MẠCH ĐIỆN
§1. Phương pháp dòng điện nhánh1
§2. Phương pháp dòng điện vòng2
§3. Phương pháp điện áp 2 nút3
§4. Biến đổi tương đương4
Chương 3. Các phương pháp tính toán mạch điện
§5. Ví dụ5

37. §1. Phương pháp dòng điện nhánh
Nội dụng:
+ Đặt ẩn số là dòng điện trong các nhánh (m nhánh  có m ẩn số)
+ Sử dụng 2 định luật Kichhop lập hệ phương trình:
+ nếu có n nút  viết được n-1 phương trình theo K1
+ và m – (n – 1) phương trình theo K2
+ Giải hệ phương trình và tìm ra ẩn số là dòng các nhánh
Ví dụ:
Cho 321 ,,

EEE
321 ,, ZZZ
Tìm các dòng điện nhánh
A
B
Z1
o
E1
Z2 Z3
o
I1
o
I2
o
I3
o
E2
o
E3
Chương 3 /

38. §1. Phương pháp dòng điện nhánh
Mạch có: n = 2 nút (A,B)
0321 

III
m = 3 nhánh
A
B
Z1
o
E1
Z2 Z3
o
I1
o
I2
o
I3
o
E2
o
E3
Chương 3 /
+ Theo K1 có n – 1 = 1 phương trình viết cho nút
+ Theo K2 có m – (n – 1) = 2 phương trình viết cho vòng
212211 ..

 EEZIZI
323322 ..

 EEZIZI
(1)
(2)
(3)
+ Giải hệ phương trình (1),(2),(3)
1VI

2VI

Chương 3 /

39. §2. Phương pháp dòng điện vòng
Nội dụng:
+ Đặt ẩn số là dòng điện vòng (chạy khép kín trong 1 vòng)
+ Sử dụng 2 định luật Kichhop lập hệ phương trình với các ẩn này
+ Giải hệ phương trình tìm ra được dòng vòng
Ví dụ:
+ Dòng điện trong các nhánh bằng tổng đại số các dòng vòng qua
nhánh đó
A
B
Z1
o
E1
Z2 Z3
o
I1
o
I2
o
I3
o
E2
o
E3
1VI

2VI

21222111 ...

 EEZIZIZI VVV
32213222 ...

 EEZIZIZI VVV
Tìm được: 21, VV II

Tính: 321 ,,

III
11 VII

 122 VV III

 23 VII


Chương 3 /

40. §3. Phương pháp điện áp 2 nút
Chú ý: Chỉ sử dụng với mạch điện có 2 nút
Nội dụng:
+ Đặt ẩn số là điện áp giữa 2 nút (mạch có 2 nút sẽ cho ta 1
phương trình 1 ẩn)
+ Sử dụng định luật K1 lập phương trình với ẩn số đó
+ Giải phương trình tìm điện áp 2 nút
+ Tìm dòng điện trong các nhánh
A
B
Z1
o
E1
Z2 Z3
o
I1
o
I2
o
I3
o
E2
o
E3
1VI

2VI

Ví dụ:
Cho 321 ,,

EEE
321 ,, ZZZ
Tìm các dòng
điện nhánh
+ Đặt ẩn là điện áp UAB
+ Tại nút A có: 0321 

III
Chương 3 /

41. §3. Phương pháp điện áp 2 nút
+ Xét từng nhánh:
1
1
1
Z
UE
I
AB

 

Z1
o
E1
o
I1
A
B
o
UAB
2
2
2
Z
UE
I
AB

 

3
3
3
Z
UE
I
AB

 

321
3
3
2
2
1
1
111
111
ZZZ
Z
E
Z
E
Z
E
U AB





321
332211
YYY
YEYEYE
U AB





Z
Y
1

Chương 3 /

42. §4. Biến đổi tương đương
1. Nhánh nối tiếp : Z1 Z2 Zn Znt
Với :
k n
nt k
k 1
Z Z


 
2. Nhánh song song :
Z1 Z2 Zn Z//
// k n
kk 1
1
Z
1
Z




Với :
k n k n
k k
k 1 k 1
R j X
 
 
   nt ntR jX 
// //R jX 
Khi có 2 Tổng trở // 1 2
1 2
Z Z
Z//
Z Z


Chương 3 /

43. §4. Biến đổi tương đương
Ví dụ 1 Z1 = 3 + j 4 ; Z2 = 8 – j 6
=> Znt = 11 – j 2
-2
jartg
2 2 11
11 2 e
- Nếu Z1 // Z2
1 2
1 2
Z Z
Z//
Z Z


j10 18'
(3 j4)(8 j6)
Z//
11,18e
 
 
- Nếu Z1 nối tiếp
Z2
j53 8' j36 52'
j10 18'
5e 10e
11,18e



 

j26 34'
4,47e

j10 18'
11,18e


Z1 Z2
ZntZnt =
Z1 Z2
Z//
Chương 3 /

44. §4. Biến đổi tương đương
Ví dụ 2
LI

XL XCUbiết U~ = 100 V; XL = XC = 10 
Tìm IL, IC , I ?
I
ICIL
Cho MĐ như hình bên:
IL IC I Z
10 10 0 
U

CI

L CI I I 
  
= 0
1 2
1 2
Z Z
Z//
Z Z


//
j10*( j10)
Z
j10 j10



 
I = 0
Z = R + j(XL – XC)
ZL = j XL
ZC = - j XC
* Vector
* Biến đổi tương đương
Cộng hưởng dòng điện
Chương 3 /

45. 3. Chuyển đổi sao (Y) tam giác ()
Biết Z1, Z2, Z3 nối sao :
Khi có Z1= Z2= Z3 = ZY
1 2
12 1 2
3
Z Z
Z Z Z
Z
  
Z1
Z2
Z3
1
3 2
1
3
2
Z12
Z23
Z31
2 3
23 2 3
1
Z Z
Z Z Z
Z
  
3 1
31 3 1
2
Z Z
Z Z Z
Z
  
Sao đối xứng
Z12= Z23= Z31 = Z = 3 ZY
Chương 3 /
§4. Biến đổi tương đương

46. 4. Chuyển đổi sao (Y)  tam giác ()
12 13
1
12 23 31
Z Z
Z
Z Z Z

 
Z1
Z2Z3
1
3 2
1
3
2
Z12
Z23
Z31
Trong đó:
23 21
2
12 23 31
Z Z
Z
Z Z Z

 
31 32
3
12 23 31
Z Z
Z
Z Z Z

 
Z12= Z21
Z13= Z31
Z23= Z32
Khi có Z12= Z23= Z31 = Z
Tam giác đối xứng
Z1= Z2= Z3 = ZY=
Z
3

Chú ý :
Chương 3 /
§4. Biến đổi tương đương

47. 5. Phương pháp xếp chồng
Trong mạch điện có nhiều nguồn kích thích, đáp ứng dòng, áp trên
mỗi nhánh bằng tổng đại số của các dòng áp thành phần ứng với
từng nguồn kích thích riêng rẽ.
Z3Z2
E3
Z1
E1
I1 I2
I3
+
1 11 13I I I
  
  2 21 23I I I  
  
3 31 33I I I  
  
=
E1
Z3Z2
Z1
I11 I21
I31
I13
I33
I23 E3
Z1
Z2 Z3
Chương 3 /
§4. Biến đổi tương đương

48. §5. Ví dụ
Ví dụ: Cho mạch điện như hình bên.
Biết:
UAB = 100 V
Giải
P, Q, S, cos toàn mạch
I1, I2 , Io , U1. Tìm :
I1, I2 , Io , UTìm :
ZoIo
U
X2
UAB
X1
R1 R2
I1
I2
A
B
AB
1
1
U
I 
Z 2 2
100
3 4


= 20 (A)
Zo = 5 + j 5 ; Z1 = 3 + j 4 ;
Z2 = 8 – j 6 ;
= 10 (A)
AB
2
2
U
I 
Z
2 2
100
8 6


TT:
Chương 3 /

49. ZoIo
U
X2
UAB
X1
R1 R2
I1
I2
A
B
- Véc tơ
- số phức
- qua P,Q,S
có thể dùng
Để tìm Io
C1. Dùng véc tơ
1I

chậm sau ABU

1 góc
1
4
arctg
3
  = 53o8’
0I

2I

2
6
arctg
8
  = 36o52’
vượt trước 1 gócABU

2I

36o52’
1I

53o8’
1I

2I

ABU

2 2
oI 20 10  = 22,36 (A)
Chương 3 /
§5. Ví dụ

50. ZoIo
U
X2
UAB
X1
R1 R2
I1
I2
A
B
AB
1
1
U
I
Z


 j0
100e
3 j4



C2. Dùng số phức
j0
j53 8'
100e
5e



j53 8'
1I 20e


AB
2
2
U
I
Z


 j0
100e
8 j6



j0
j36 52'
100e
10e



j36 52'
2I 10e

o 1 2I I I 
  
j53 8'
20e


j36 52'
10e

12 j16  8 j6  = 20 – j 10
j26 34'
oI 22,36e



Chọn gốc V100100eU
o
j0
AB 

Chương 3 /
§5. Ví dụ

51. ZoIo
U
X2
UAB
X1
R1 R2
I1
I2
A
B
2 2
ABAB ABS P Q 
Cụm AB
PAB = R1I1
2 + R2I2
2
PAB = 3.202 + 8.102 = 2000 W
QAB = X1I1
2 - X2I2
2 = 4.202 - 6.102 = 1000 VAr
2 2
2000 1000  = 2236 VA
AB AB oS U I AB
o
AB
S
I
U

2236
100
 = 22,36 A
C3. Dùng qua P,Q, S
Chương 3 /
§5. Ví dụ

52. 2 2
S P Q 
P = RoIo
2 + PAB
P = 5.22,362 + 2000 = 4500 W
2 2
4500 3500  = 5700 VA
oS U I
o
S
U
I

5700
22,36
 = 255 V
2. Tìm P, Q, S, cos toàn mạch
Q = XoIo
2 + QAB
Q = 5.22,362 + 1000 = 3500 VAr
P
cos
S
 
4500
5700
 = 0,79
ZoIo
U
X2
UAB
X1
R1 R2
I1
I2
A
B
Cụm AB
Chương 3 /
§5. Ví dụ

53. PHẦN I. MẠCH ĐIỆN
Khái niệm chung về MĐ xoay chiều 3 pha1
Quan hệ giữa các đại lượng dây và pha trong mạch 3
pha đối xứng
2
Công suất trong mạch 3 pha3
Phương pháp tính toán mạch 3 pha4
Chương 4. Mạch 3 pha
Ví dụ5

54. Ae 2.E.sin t 
o
Be 2.E.sin( t 120 )  
o
Ce 2.E.sin( t 240 )  
1. Nguồn 3 pha:
ĐN: Nguồn 3 pha là tổ hợp 3 nguồn 1 pha có sđđ lệch nhau về thời
gian
Nguồn 3 pha đối xứng:
+ Là một nguồn 3 pha có biên độ các pha bằng nhau
+ Lệch pha nhau liên tiếp 1 góc 1200
Ký hiệu:
Pha thứ nhất là A:
Pha thứ hai là B:
Pha thứ hai là C:
§1 – Khái niệm chung về MĐ xoay chiều 3 pha
Chương 4

55. eC
eA eB
0 1 2 3 4 5 6
-1
-0.5
0
0.5
1
120
o
240
o
360
o
e
t
1. Nguồn 3 pha:
Nguồn 3 pha thường được lấy từ máy phát 3 pha
- Biểu diễn phức:
j0
AE Ee



j120
BE Ee




j240
CE Ee




Với nguồn 3 pha đối xứng luôn có :
A B CE E E
  
   0
j120
CE Ee




Hoặc
Chương 4
§1 – Khái niệm chung về MĐ xoay chiều 3 pha

56. - Biểu diễn vector:
A B CE E E  
  
A B Ce e e  
A B CE E E
  
  
0
AE

BE

CE

120o
Chương 4
§1 – Khái niệm chung về MĐ xoay chiều 3 pha

57. - Cách nối nguồn:
+ Nối Y:
3 điểm cuối nối với nhau thành điểm trung tính của nguồn.
Ký hiệu : O
+ Nối  (D):
Cuối của pha này nối với đầu của pha kia.
Chương 4
§1 – Khái niệm chung về MĐ xoay chiều 3 pha

58. 2. Phụ tải
- Gồm 2 loại:
- Phụ tải 1 pha mắc trong mạch 3 pha. Vd: quạt, đèn, …
- Phụ tải 3 thuần túy (chỉ hoạt động trong mạch 3 pha)
 Vậy các phụ tải được mắc như thế nào? Y hay D
- Phụ tải nối Y hay D là phụ thuộc vào điện áp định mức cảu tải và
nguồn điện để nó có thể làm việc bình thường.
Chương 4
§1 – Khái niệm chung về MĐ xoay chiều 3 pha

59. §2 – Quan hệ giữa các đại lượng dây và pha trong
mạch 3 pha đối xứng
1. Định nghĩa
- Mạch 3 pha đối xứng:
+ Nguồn 3 pha đối xứng
+ Tải 3 pha đối xứng (bao gồm cả đường dây đối xứng)
Trong đó: tải ba pha đx là tải có tổng trở các pha bằng nhau
- Đại lượng pha:
+ Điện áp pha: Uf , Up
+ Dòng điện pha: If , Ip
- Đại lượng dây:
+ Điện áp dây: Ud
+ Dòng điện dây: Id
Chương 4

60. 2. Mạch nối Y
ZC
ZA
ZB
EA
EC
EB
O O’
IB
IA
IC
Uo’o
UAB
UCA
UBC
UA
UC
UB
UAB
Chương 4 §2 – Quan hệ giữa các đại lượng dây và pha trong mạch 3
pha đối xứng
AB A BU U U 
  
BC B CU U U 
  
CA C AU U U 
  

61. 2. Mạch nối Y
AU

BU

CU

ABU

BCU

CAU

- Về trị hiệu dụng :
- Về góc pha :
d fU 3U
d fI I
30O
Điện áp dây vượt trước điện áp pha 1 góc 300
CAU

CU

vượt trước góc 30o
Chương 4 §2 – Quan hệ giữa các đại lượng dây và pha trong mạch 3
pha đối xứng

62. 3. Mạch nối D
UB
C
UA
B
UCA
IABICA
IBC
B BC ABI I I 
  
C CA BCI I I 
  
Tại A :
A AB CAI I I 
  
C
D A
B
ZCA
ZAB
ZBC
E BA
EAC
ECB
IB
IA
IC
C
UAB
Chương 4 §2 – Quan hệ giữa các đại lượng dây và pha trong mạch 3
pha đối xứng

63. 3. Mạch nối D
AI

BI

CI

- Về giá trị
hiệu dung:
B BC ABI I I 
  
C CA BCI I I 
  
A AB CAI I I 
  
d fU U
d fI 3I
- Về góc pha :
ABI

góc 30o
AI

Chậm sau
BCI

CAI

ABI


BCU

ABU

CAU

Dòng điện dây chậm sau dòng điện pha 1 góc 300
Chương 4 §2 – Quan hệ giữa các đại lượng dây và pha trong mạch 3
pha đối xứng

64. §3 – Công suất trong mạch 3 pha
1. Công suất tác dụng:
PA , PB, PC
Tải đối xứng:
Tải nối Y : d
f
U
U
3
 If = Id
P3f = PA + PB+ PC
P = 3Pf = 3UfIfcosf = 3RIf
2
d dP 3U I cos 
Tải nối  (D):
f dU U
d
f
I
I
3

P 3U I cos 
Chương 4

65. Để đo P3f :
* PP 1 oat kế :
W

* PP 2 oat kế :
Pf
Tải 3 pha
ĐX or KHĐX
nối Y or 
W

W


1
2
P3f = PA + PB + PC
P3f = 3 PfĐX:
KĐX:
1 2P P P 
W
1
W
2

cùng chiều

ngược chiều
Chương 4
§3 – Công suất trong mạch 3 pha

66. 2. Công suất phản kháng:
Q = 3Qf = 3UfIfsinf
Tải nối Y hay : Q 3U I sin 
QA , QB, QC Q3f = QA + QB+ QC
= 3XIf
2Khi tải đối xứng :
3. Công suất biểu kiến (CS toàn phần)
2 2
S P Q = 3 U I 
Chương 4
§3 – Công suất trong mạch 3 pha

67. §4 – Phương pháp tính toán mạch 3 pha
1. Mạch nối Y :
Cho mạch điện:
+ nguồn 3 pha đối xứng : A B CE ,E ,E ,
  
+ tải 3 pha : A B CZ , Z , Z ,
 Tính dòng điện trong các pha
'A O O
A
A
E U
I
Z
 
 

- Tìm được điện áp UO’O
- Tính dòng điện:
 ,B CI I
 
'
0
0
O O
A B C
U
I I I I
Z

   
   
'
0
1 1 1
1 1 1 1
A B C
A B C
O O
A B C
E E E
Z Z Z
U
Z Z Z Z
  

 

  
ZA
o
E1
o
IA
ZB
o
E2
o
IB
ZC
o
E3
o
IC
O'O
Z0
o
Io
Chương 4

68. 1. Mạch nối Y :
- Đặc biệt:
b/ khi mạch đối xứng A B CZ Z Z
  
 
a/ Z0 = 0 ' 0O OU


A
A
A
E
I
Z


 B
B
B
E
I
Z


 C
C
C
E
I
Z



'
0
1
( )
0
3 1
A B C
O O
E E E
Z
U
Z Z
  

 
 

 Uf nguồn = Uf tải
fI fU

Z
Tính toán tương tự cho các pha còn lại bằng cách suy ra từ góc
lệch pha 1200
ZA
o
E1
o
IA
ZB
o
E2
o
IB
ZC
o
E3
o
IC
O'O
Z0
o
Io
Chương 4
§4 – Phương pháp tính toán mạch 3 pha

69. 1. Mạch nối  (D) :
A
B
C
ZAB
o
Ud
ZBC
ZCA
o
IAB
o
IBC
o
ICA
o
IA
o
IB
o
IC
Cho mạch điện:
+ Cho điện áp: dU
+ tải 3 pha : A B CZ , Z ,Z ,
 Tính dòng điện trong các pha, dây
; ;B C C AA B
A B B C C A
A B B C C A
U UU
I I I
Z Z Z
 
  
  
A A B C AI I I
  
 
B B C A BI I I
  
 
C C A B CI I I
  
 
- mạch 3 pha nối  đối xứng:
AB BC CAZ Z Z Z
  
  
fd
A B
UU
I  
ZZ
3A d fI I I 
Chương 4
§4 – Phương pháp tính toán mạch 3 pha

70. §5– Ví dụ
VD1: Trường hợp mạch 3 pha
không đối xứng
Cho mạch điện nối Y:
A
B
C
o
Ud
R
R
R
O'
Cho : Ud = 380 V
R = 10 
a. Tìm : If, Id, P
b. Đứt dây pha A, xác định độ
sáng của đèn
c. Ngắn mạch pha A, xác định độ sáng của đèn
d. Tắt ½ số đèn của pha A, xác định độ sáng của đèn
Chương 4

71. VD1:
A
B
C
o
Ud
R
R
R
O'
a. Tìm : If, Id, P
- mạch 3 pha đối xứng nối Y
' 0O OU


Uf nguồn = Uf tải = 220 V
220
22( )
10
f
AB d
U
I A I
R
   
2
3. . fP R I 2
3.10.22 14520W 
b. Khi đứt dây pha A
- Để xác định độ sáng của các đèn  cần xác định điện áp trên
các pha
Chương 4
§5– Ví dụ

72. Chương 4 /
VD1:
b. Khi đứt dây pha A A
B
C
o
Ud
R
R
O'
- Pha A tắt
- Mạch tương đương
- Điện áp trên 2 pha B và C
- Pha B,C đèn tối hơn
2
d
f
U
U 
380
190( )
2
V  220( )dmU V 
c. Ngắn mạch pha A
- Pha A tắt
- Điện áp trên 2 pha B và C
fB fCU U 380( )dU V 
Chương 4
§5– Ví dụ

73. Chương 4 /
VD1:
d. Tắt ½ đèn của pha A
- Tổng trở pha A: 'AR  20( )
 Mạch 3 pha không đối xứng, không có dây trung tính
'
1 1 1
1 1 1
A B C
A B C
O O
A B C
U U U
R R R
U
R R R
  

 

 
1 1 1
20 10 10
1 1 1
20 10 10
A B CU U U
  
 

 
2
5
2
A
B C
U
U U

 
 

- Dùng đồ thị véctor
'O OU

' 264( )AU V
' ' 220( )B CU U V  220
0 AU

CU

BU

Chương 4
§5– Ví dụ

74. Chương 4 /
VD2:
Cho mạch điện:
Cho : Up = 220 V
Xc = 10 
R = 10 
Xác định độ sáng của 2 đèn
R R
Xc
C
B
A
O'
Chương 4
§5– Ví dụ

75. Chương 4 /Chương 4
jb
jX
1
Y
C
A 

 g
R
1
YY CB 
ggjb
gegejb
UU
oo
120j120j
pO'O





    866,0j5,0120sinj120cose oo120j o

866,0j5,0120sinj120cose oo120j o

   
ggjb
866,0j5,0g866,0j5,0gjb
UU pO'O


 
 6,0j2,0UU pO'O 
Nếu chọn g = b
Nguồn điện ba pha đối xứng có điện áp pha là Up
Theo phương pháp điện áp hai nút:
Với:
R R
Xc
C
B
A
O'
§5– Ví dụ

76. Chương 4 /Chương 4
     466,1j3,0U6,0j2,0U866,0j5,0UUUU pppO'OB
'
B  
p
22
p
'
B U5,1466,13,0UU 
     266,0j3,0U6,0j2,0U866,0j5,0UUUU pppO'OC
'
C  
p
22
p
'
C U4,0266,03,0UU 
Điện áp đặt lên bóng đèn
pha B và pha C:
Ta thấy U’B > U’C nên bóng đèn pha B sáng hơn bóng đèn pha C, điện
áp ở các pha tải khác điện áp ở pha nguồn
R R
Xc
C
B
A
O'
§5– Ví dụ