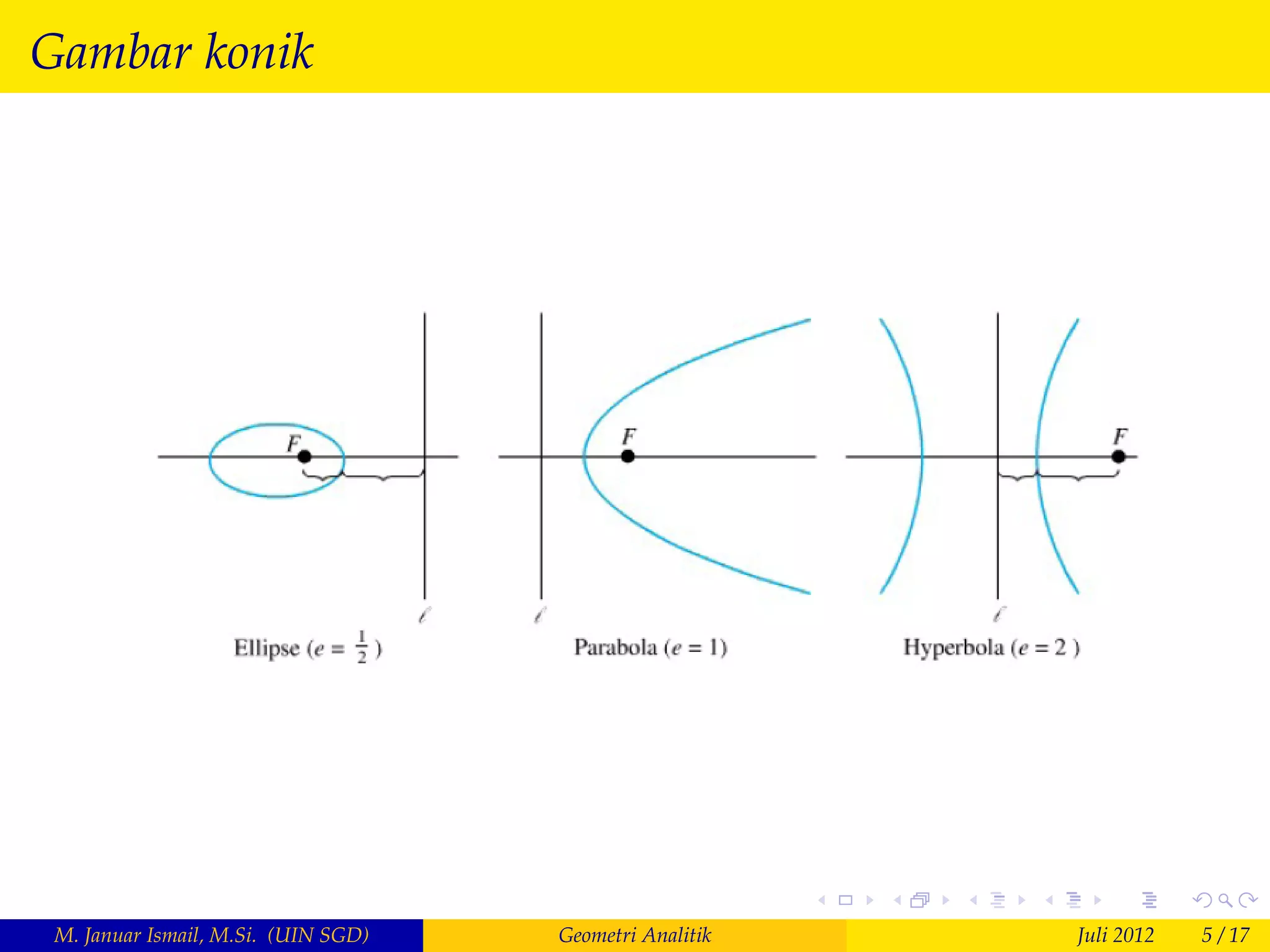
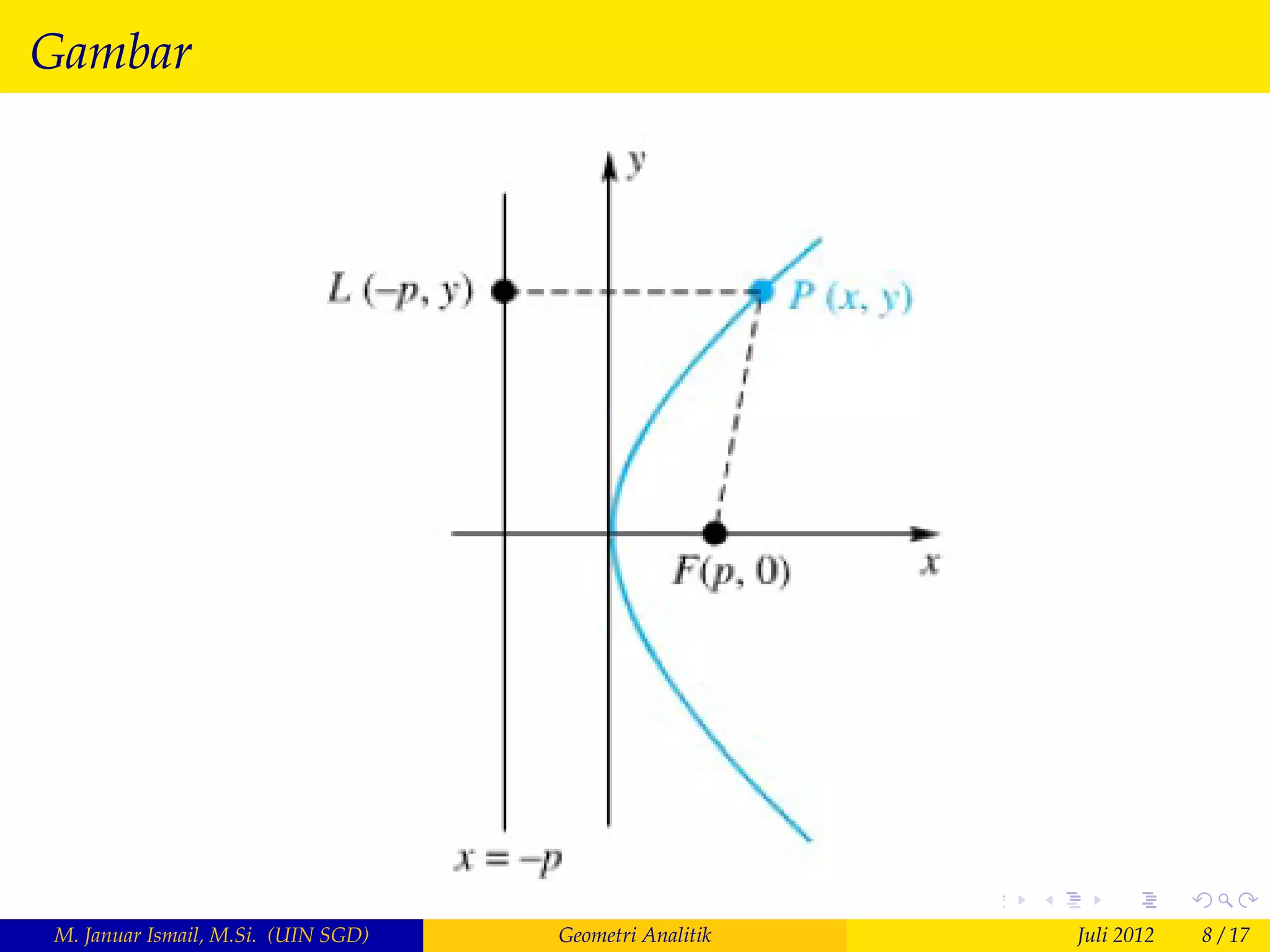
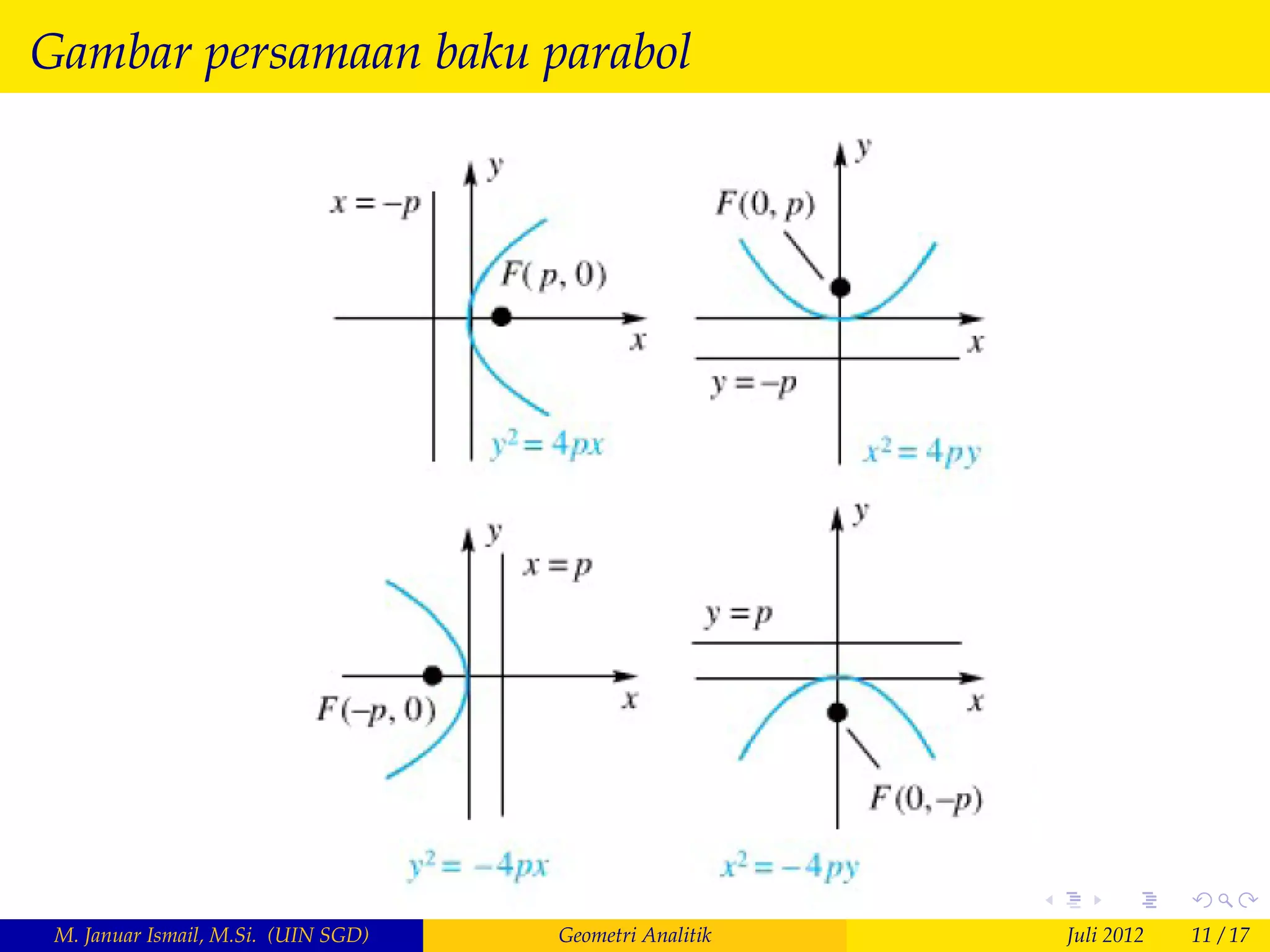
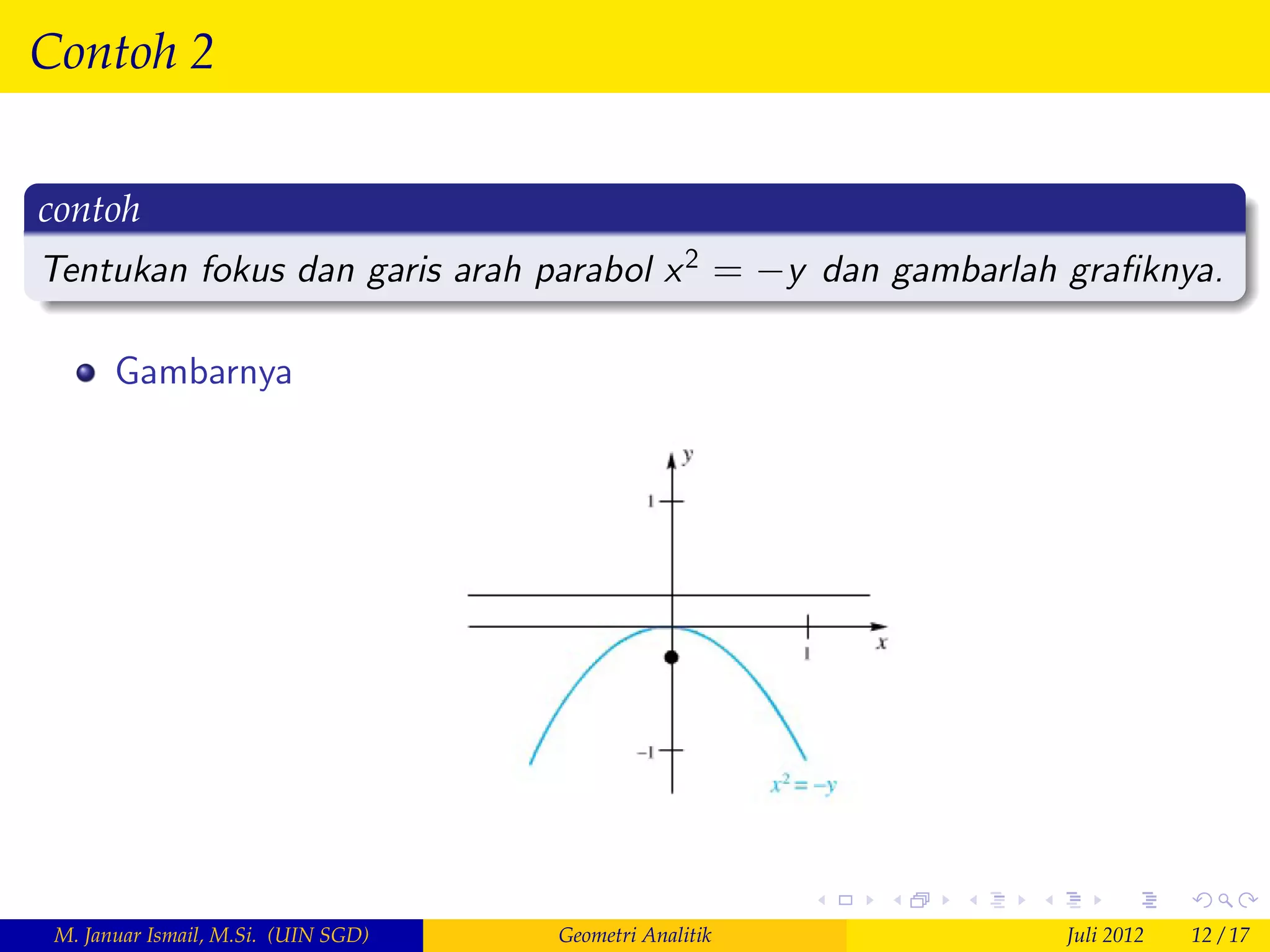
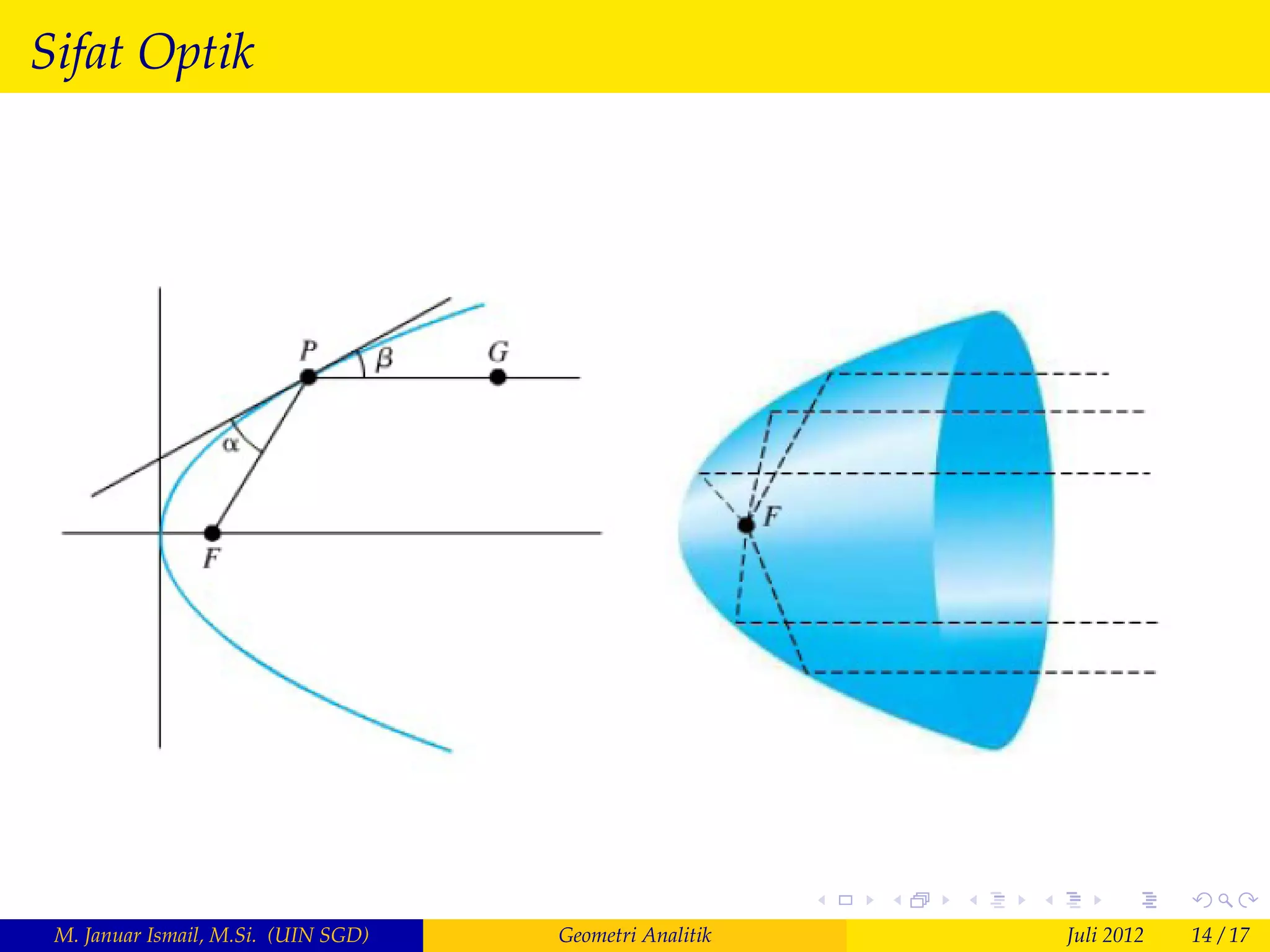
Dokumen tersebut membahas tentang geometri analitik khususnya konik, yang meliputi definisi dan contoh soal parabol. Parabol didefinisikan sebagai kurva titik yang jaraknya sama dari fokus dan garis arah. Persamaan parabol dapat ditentukan dan tergantung pada posisi fokus dan garis arah. Sifat optik parabol yakni sinar cahaya yang jatuh dan terpantul pada parabol akan sejajar juga dibuktikan.

1. Geometri Analitik
M. Januar Ismail, M.Si.
UIN SGD
Juli 2012
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 1 / 17

2. Outline
1 Irisan Kerucut (konik) dan koordinat kutub
Konik
Parabol
Contoh
Sifat Optik
Referensi
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 2 / 17

3. Irisan Kerucut (Konik)
Ambillah sebuah kerucut lingkaran tegak, dengan dua cabangya. Kita
potong kerucut tersebut dengan berbagai bidang dengan sudut
berbeda terhadap sumbu simetri, seperti gambar di bawah ini. bidang
tersebut memotong kurva-kurva, masing-masing dinamakan elips,
parabol dan hiperbol. kurva-kurva tersebut dinamakan irisan kerucut
atau konik. selanjutnya kita berikan de…nisi yang lain mengenai
kurva-kurva tersebut.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 3 / 17

4. Definisi Konik
Definisi
Pada sebuah bidang ada garis l tetap (garis arah) dan F sebuah titik tetap
(fokus) yang tidak terletak pada garis l .Himpunan titik-titik P yang
perbandingan antara jarak jPF j dari fokus dan jarak jPLj dari garis arah
adalah suatu konstanta positif e (keeksentrikan), yakni yang memenuhi
hubungan
jPF j = e jPLj
dinamakan Konik. Apabila 0 < e < 1, konik dinamakan elips, apabila
e = 1 dinamakan parabol, dan e = 2 dinamakan hiperbol.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 4 / 17

5. Gambar konik
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 5 / 17

6. Konik
Pada gambar sebelumnya dapat kita lihat masing-masing kurva untuk
e = 1/2, e = 1, dan e = 2.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 6 / 17

7. Konik
Pada gambar sebelumnya dapat kita lihat masing-masing kurva untuk
e = 1/2, e = 1, dan e = 2.
Untuk setiap kasus, kurva-kurva tersebut simetrik terhadap garis yang
melalui fokus dan tegak lurus terhadap garis arah. garis ini kita sebut
sumbu panjang dari konik. titik yang merupakan titik potong sumbu
dengan konik disebut puncak.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 6 / 17

8. Definisi
Definisi
Parabol (e = 1) Sebuah parabol adalah himpunan titik-titik P yang
berjarak sama daria arah l dan fokus F , yakni memenuhi hubungan
jPF j = jPLj .
Kita dapat menentukan persamaan xy dari parabol dan persamaannya
berupa persamaan sederhana
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 7 / 17

9. Definisi
Definisi
Parabol (e = 1) Sebuah parabol adalah himpunan titik-titik P yang
berjarak sama daria arah l dan fokus F , yakni memenuhi hubungan
jPF j = jPLj .
Kita dapat menentukan persamaan xy dari parabol dan persamaannya
berupa persamaan sederhana
kedudukan sumbu koordinat tidak mempengaruhi bentuk kurva,
tetapi kedudukan tersebut dapat mempengaruhi kesederhanaan
persamaan kurva
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 7 / 17

10. Definisi
Definisi
Parabol (e = 1) Sebuah parabol adalah himpunan titik-titik P yang
berjarak sama daria arah l dan fokus F , yakni memenuhi hubungan
jPF j = jPLj .
Kita dapat menentukan persamaan xy dari parabol dan persamaannya
berupa persamaan sederhana
kedudukan sumbu koordinat tidak mempengaruhi bentuk kurva,
tetapi kedudukan tersebut dapat mempengaruhi kesederhanaan
persamaan kurva
Oleh karena sebuah parabol itu simetrik terhadap sumbunya, maka
sudah lazim kita tempatkan salah satu sumbu koordinat misalnya
sumbu x pada sumbu simetri kurva.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 7 / 17

11. Definisi
Definisi
Parabol (e = 1) Sebuah parabol adalah himpunan titik-titik P yang
berjarak sama daria arah l dan fokus F , yakni memenuhi hubungan
jPF j = jPLj .
Kita dapat menentukan persamaan xy dari parabol dan persamaannya
berupa persamaan sederhana
kedudukan sumbu koordinat tidak mempengaruhi bentuk kurva,
tetapi kedudukan tersebut dapat mempengaruhi kesederhanaan
persamaan kurva
Oleh karena sebuah parabol itu simetrik terhadap sumbunya, maka
sudah lazim kita tempatkan salah satu sumbu koordinat misalnya
sumbu x pada sumbu simetri kurva.
kita pilih fokus F di sebelah kanan titik asal, misalnya (p, 0). garis
arah kita pilih di sebelah kirinya dengan persamaan x = p. Dengan
demikian, puncak parabol ada di titik asal sistem koordinat.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 7 / 17

12. Gambar
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 8 / 17

13. Parabol
Dari syarat jPF j = jPLj dan rumus jarak, dapat diperoleh
q q
(x p )2 + (y 0)2 = (x + p )2 + (y y )2
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 9 / 17

14. Parabol
Dari syarat jPF j = jPLj dan rumus jarak, dapat diperoleh
q q
(x p )2 + (y 0)2 = (x + p )2 + (y y )2
Setelah disederhanakan diperoleh
y 2 = 4px
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 9 / 17

15. Parabol
Dari syarat jPF j = jPLj dan rumus jarak, dapat diperoleh
q q
(x p )2 + (y 0)2 = (x + p )2 + (y y )2
Setelah disederhanakan diperoleh
y 2 = 4px
Persamaan ini disebut persamaan baku sebuah parabol mendatar
(artinya sumbu simetrisnya mendatar) dan terbuka ke kanan,
perhatikan bahwa p > 0 dan p merupakan jarak dari fokus ke
puncaknya.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 9 / 17

16. Contoh 1
contoh
Tentukan fokus dan garis arah parabol y 2 = 12x.
Penyelesaian : Oleh karena y 2 = 4(3)x, maka p = 3 sehingga fokus
ada di (3, 0) dan garis arah adalah x = 3.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 10 / 17

17. Contoh 1
contoh
Tentukan fokus dan garis arah parabol y 2 = 12x.
Penyelesaian : Oleh karena y 2 = 4(3)x, maka p = 3 sehingga fokus
ada di (3, 0) dan garis arah adalah x = 3.
Ada tiga persamaan baku dari parabol selain persamaan di atas.
apabila x dan y dipertukarkan, dan tanda negatif pada salah satu
ruas persamaan parabol kita peroleh parabol yang terbuka ke arah
yang berlawanan. Keempat jenis parabol tersebut dapat dilihat pada
gambar selanjutnya.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 10 / 17

18. Gambar persamaan baku parabol
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 11 / 17

19. Contoh 2
contoh
Tentukan fokus dan garis arah parabol x 2 = y dan gambarlah gra…knya.
Gambarnya
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 12 / 17

20. Contoh 3 dan 4
contoh
Tentukan persamaan parabol dengan puncak di titik asal dan berfokus di
(0, 5).
contoh
Tentukan persamaan parabol dengan puncak di titik asal, yang melalui
( 2, 4) dan terbuka ke kiri. Gambarkan parabolnya.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 13 / 17

21. Sifat Optik
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 14 / 17

22. Sifat Optik
Sifat Parabol di atas dipakai untuk membuat lampu sorot dan pada
teleskop
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 15 / 17

23. Sifat Optik
Sifat Parabol di atas dipakai untuk membuat lampu sorot dan pada
teleskop
Selanjutnya buktikan sifat optik parabol di atas.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 15 / 17

24. Bukti sifat optik parabol
Perhatikan gambar
Kita harus membuktikan bahwa sudut α = β.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 16 / 17

25. Bukti sifat optik parabol
Perhatikan gambar
Kita harus membuktikan bahwa sudut α = β.
Oleh karena FQP = β, maka cukup dibuktikan bahwa 4FQP sama
kaki.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 16 / 17

26. Referensi
1 Purcell dan Dale, Kalkulus dan Geometri analitik jilid 2.
M. Januar Ismail, M.Si. (UIN SGD) Geometri Analitik Juli 2012 17 / 17