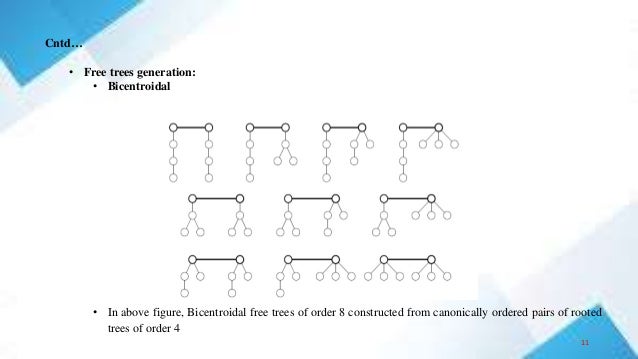
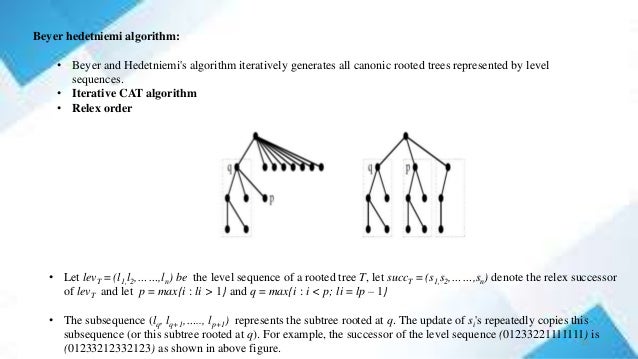
The document discusses the generation of free and rooted trees, detailing various algorithms including the iterative and recursive cat algorithms and the wrom algorithm. It explains concepts like level representation, canonical ordering, and weight sequences, along with the characteristics of unicentroidal and bicentroidal trees. The conclusion emphasizes the effectiveness of the discussed algorithms and their adaptability to specific constraints.

1. Generation of Free Trees and
Rooted Trees
BY
PURBASHA CHOWDHURY
97/CSM/201013
1

2. CONTENTS:
• INTRODUCTION
• TREE GENERATION
• ROOTED TREES
• FREE TREES
• WEIGHT SEQUENCE OF ORDERED TREES
• ROOTED TREES
• FREE TREES
• COMPARATIVE STUDY OF ALGORITHMS
• ITERATIVE CAT ALGORITHM
• RECURSIVE CAT ALGORITHM
• WROM ALGORITHM
• CONCLUSION
2

3. Introduction:
• A tree is considered as a free tree.
• A rooted tree can be differentiated by one vertex which is nothing but a root.
• Labelled rooted tree
• Preorder labelling
A preordered labeled rooted tree with root 1
3

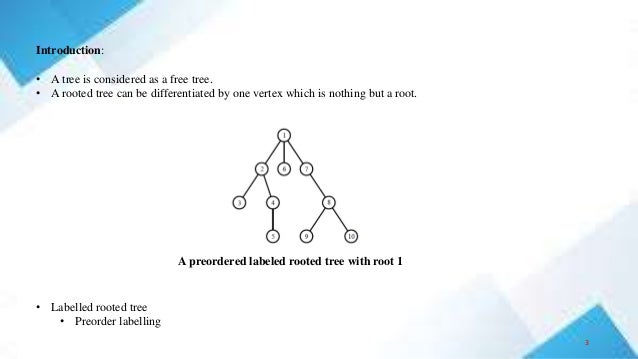
4. Tree generation:
• The trees are labelled, and then form a sequence of the nodes using the labels assigned to them, which
defines the structure of the tree.
• For rooted trees and free trees, positive numbers 1, 2, …, n are used as labels, so the sequences which
represent these trees are of positive integers
• In above diagram, basically two types of sequences of tree T are shown which are represented by two arrays
which are basically level sequence (levT [1,…,n]) and parent sequence(parT [1,….,n]).
4

5. Cntd…..
• Rooted trees:
• Level representation:
• Provides a linear order of subtrees.
• Isomorphic trees
• Adjacent subtrees i.e., consecutive subsequence
An ordered, rooted tree T, with vertex levels shown, and its level sequence
• The level of a vertex v, lv, to be 1 if v is the root; or one greater than the level of its parent,
where v’s parent is the adjacent vertex on the path from v to the root
5

6. Cntd…..
• Canonical representation:
• The canonical ordering of T will be that ordered tree T* which dominates all other ordered trees T’
corresponding to T, i.e. L(T*)> L(T’) for all T’ corresponding to T. The canonical level sequence by
L(T)* is denoted
Two ordered trees with T1 dominating T2
• These are the only distinct trees corresponding to T, and since L(T1) > L(T2), L(T)* = [1 2 3 3 2]
• Successor function
• Successor of L(T) to be the sequence s(L(T))=[s1,s2 …. sn], where (i) si = li for i= 1, 2,..., p-l, (ii) si = si-
(p-q) for i = p, …..,n
6

7. • Free Trees:
• Level representation:
• Listing the level of each vertex of a rooted tree in preorder.
• The traversal must visit the roots of adjacent subtrees in nonincreasing lexicographic order
• Canonical representation
• Greatest of all level sequences describing that same tree
• The canonical sequence of rooted trees L(T,z) will be denoted by L*(T, z).
• Extracting the non isomorphic subset of rooted trees by root selection
• Refining the canonicity criteria only primary level sequence.
• Generating all primary level sequence of given size.
• Lexicographical order
• Additionally, An index is added on with the first element of one level sequence which is not
the same as the corresponding element of another level sequence.
7

8. • Weight Sequence of ordered trees:
• Rooted trees:
• The weight of each vertex in a pre-order traversal of the tree.
• For the tree R in above figure, the weight sequence ws(R) = 10 6 4 1 1 1 1 2 1 1.
8

9. Cntd….
• Canonical weight sequence:
• An ordered tree R of order n is canonically ordered if ws(R(u)) ≥ ws(R(v)), for each vertex u
of R having a next sibling v.
• r-isomorphic
• o-isomorphic
• in above figure, Two trees that are r-isomorphic but not o-isomorphic. They are not
canonically ordered,
9

10. Cntd…
• Weight Sequence of ordered trees:
• Free trees generation:
• Unicentroidal
• in above figure, Canonically ordered trees corresponding to unicentroidal free trees of order 8
10

11. Cntd…
• Free trees generation:
• Bicentroidal
• In above figure, Bicentroidal free trees of order 8 constructed from canonically ordered pairs of rooted
trees of order 4
11

12. Comparative study of Algorithms:
• As for lexicographic order, there are some variants :
• Relex order
• Colex order
• Gray code
• Generation of algorithm:
• Iterative
• Recursive
• CAT (Constant Amortized Time) algorithm
12

13. Beyer hedetniemi algorithm:
• Beyer and Hedetniemi's algorithm iteratively generates all canonic rooted trees represented by level
sequences.
• Iterative CAT algorithm
• Relex order
• Let levT = (l1,l2,……,ln) be the level sequence of a rooted tree T, let succT = (s1,s2,……,sn) denote the relex successor
of levT and let p = max{i : li > 1} and q = max{i : i < p; li = lp – 1}
• The subsequence (lq, lq+1,….., lp+1) represents the subtree rooted at q. The update of si's repeatedly copies this
subsequence (or this subtree rooted at q). For example, the successor of the level sequence (01233221111111) is
(01233212332123) as shown in above figure.
13

14. Beyer hedetniemi algorithm:
• Recursive CAT algorithm
• Depth first search manner is maintained to find canonic trees
• In above figure, subtrees up to 5 nodes are shown.
• Uses a constant amount of computation at each node of the computation tree.
• The node of subtree is proportional to the number of rooted trees with n nodes.
14

15. WROM Algorithm:
• Wright, Richmond, Odlyzko and McKay referred to as WROM Algorithm
• adopts canonic level sequences for rooted trees as the representation of unlabelled free tree.
• if T is unicentral, then c is the root if c is the center of T, or
• if T is bicentral with two centers, c, d, then c is the root if
(2.1) |Q(c)| ≥ |R(d)| and (2.2) if |Q(c)| = |R(d)|, then levQ(c) ≥ levR(d)
• The WROM algorithm trys to use the successor function.
• WROM's algorithm generates unlabelled free trees in Constant Amortized Time (CAT).
15

16. Cntd….
• WROM iterative algorithm adopted the idea from the Beyer-Hedetniemi algorithm for generating rooted trees.
• For unicentral free trees, the WROM algorithm picks the unique centre as the root and arranges the subtrees of
the resulting rooted tree recursively so that the subtrees on the left are always lexicographically bigger or equal
to the ones on the right.
• But for bicentral free trees, there are two centres. By deleting the edges between these two centres we have two
rooted subtrees.
• The goals are, first, to maintain the same natural canonic representation of free trees extended from that of rooted
trees, and second, to develop a simpler, more flexible recursive algorithm for generating free trees in relex order.
16

17. Conclusion:
• There are several algorithms to generate the rooted and free trees as iterative manner and
recursive as well. Three of them are discussed to prove the efficiency of the algorithms.
• The algorithms can be easily modified under some specific parameters such as parenthood
constraints or height restrictions.
17

18. 18