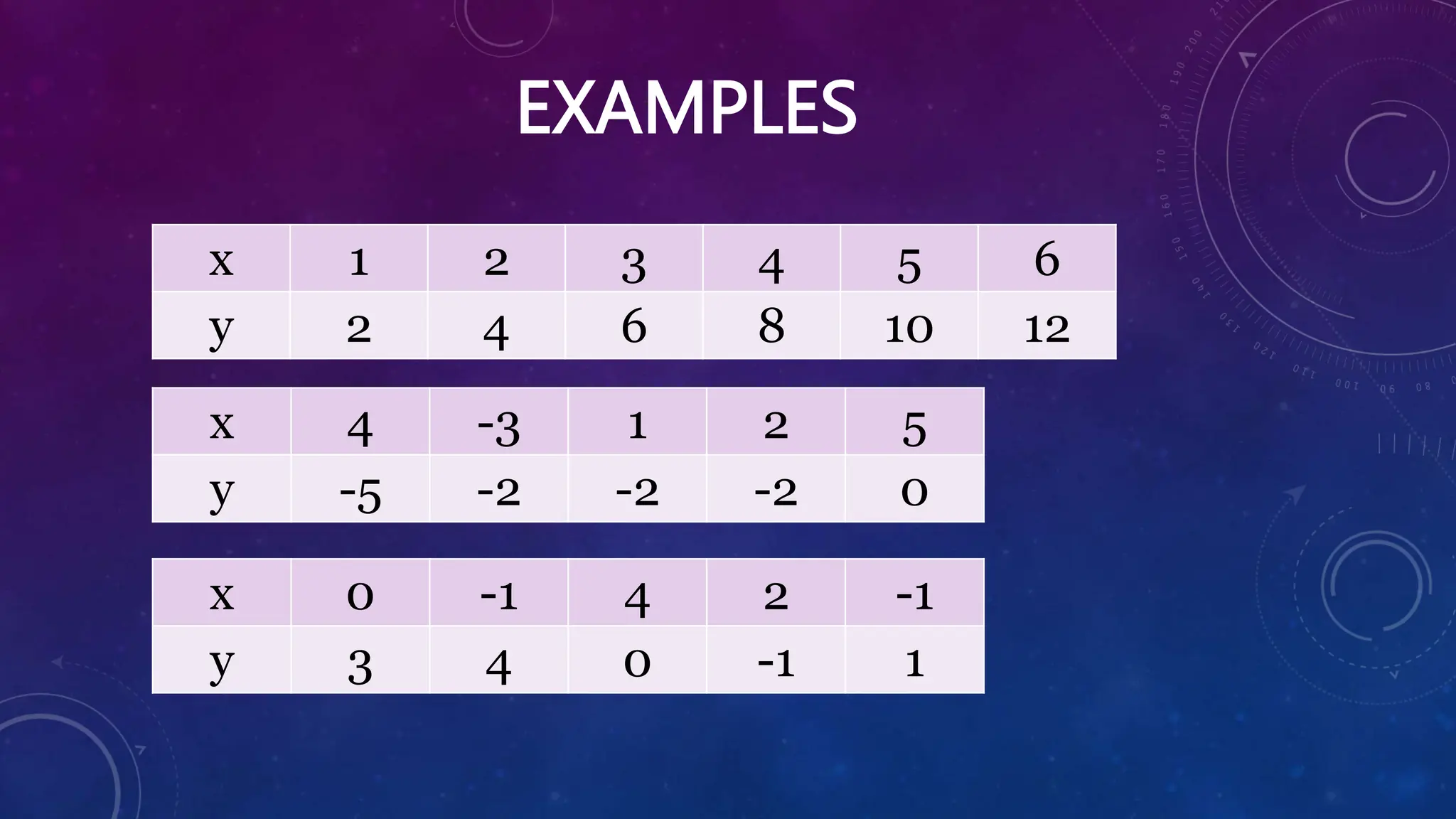
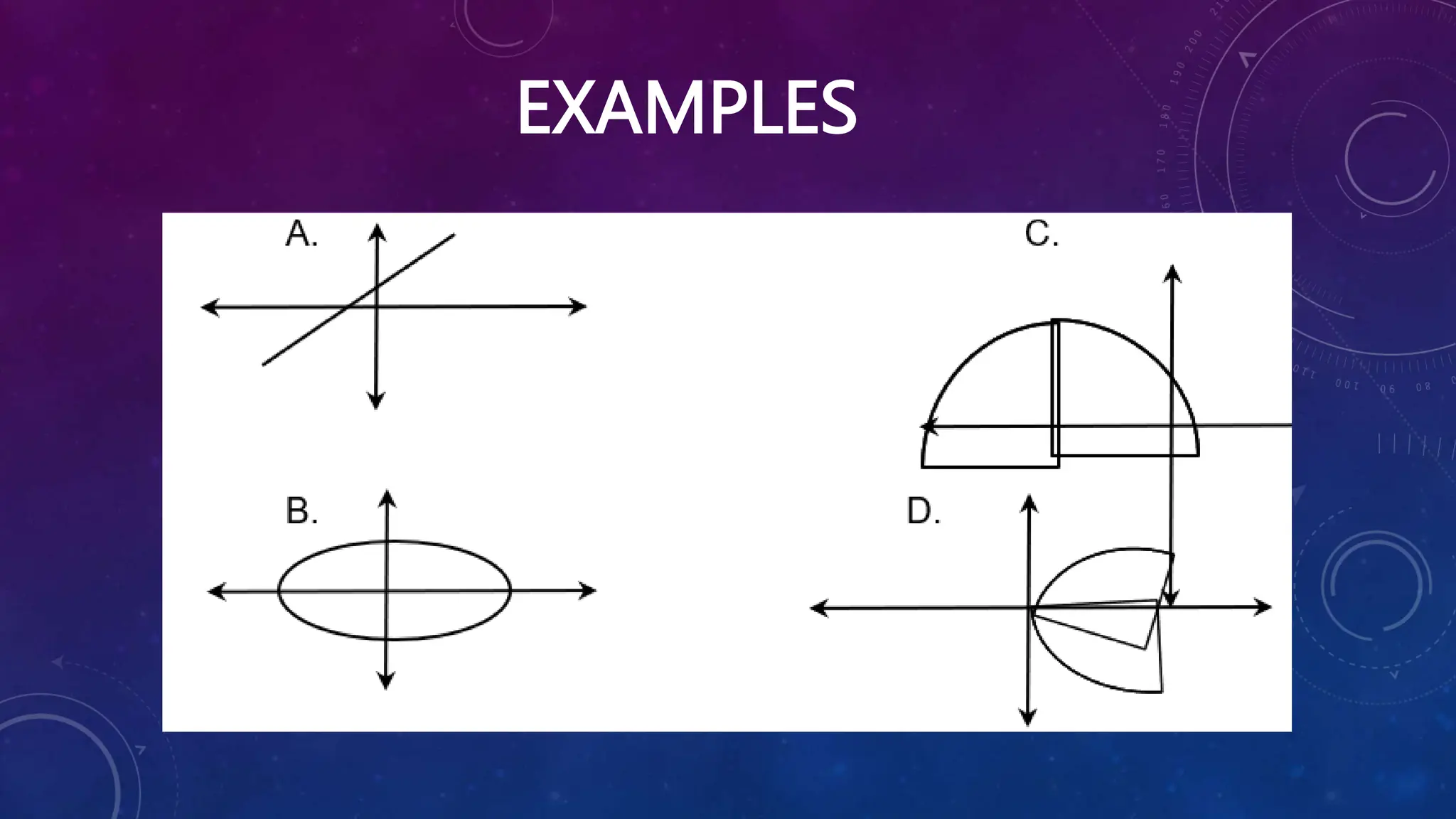
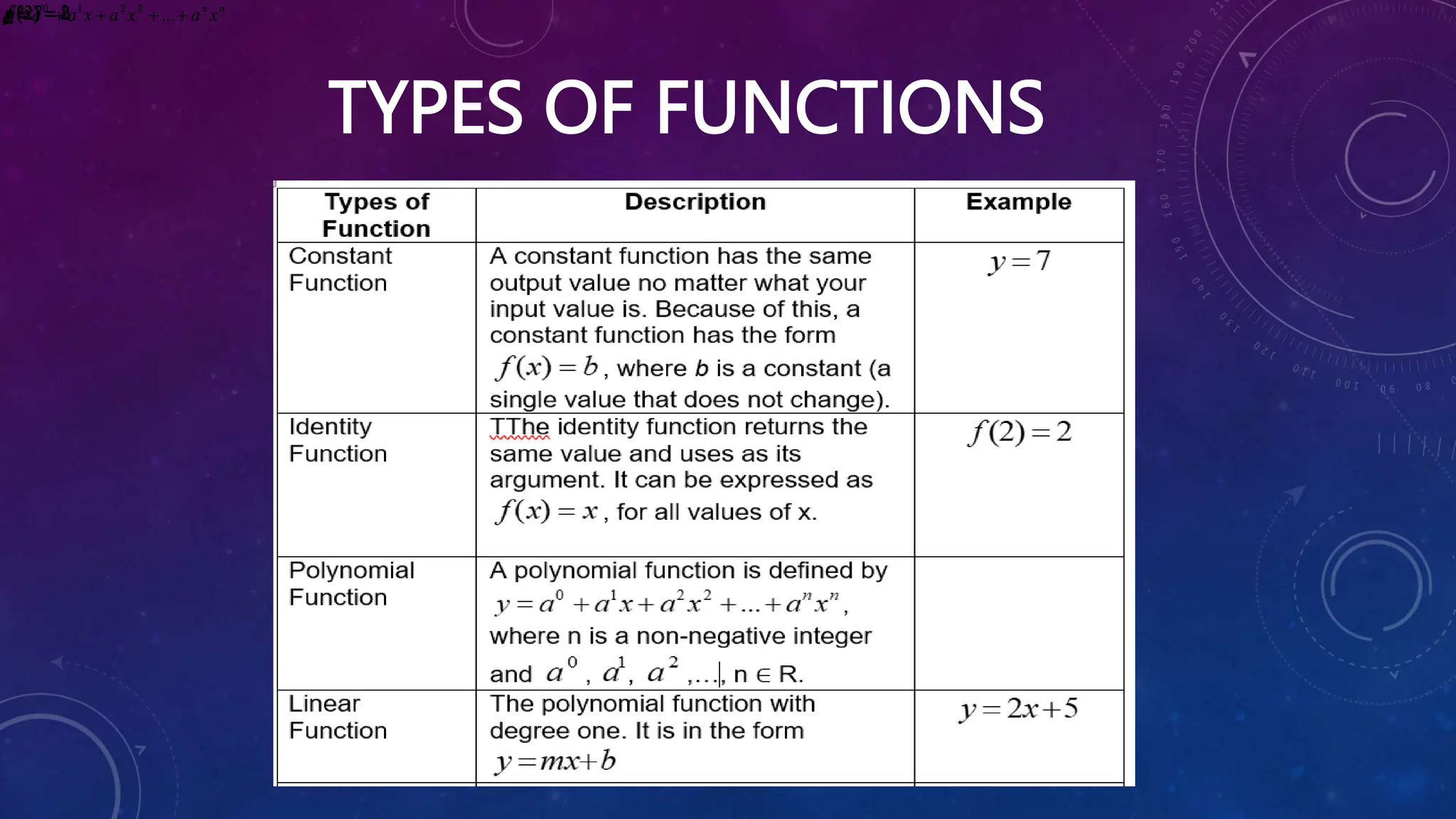
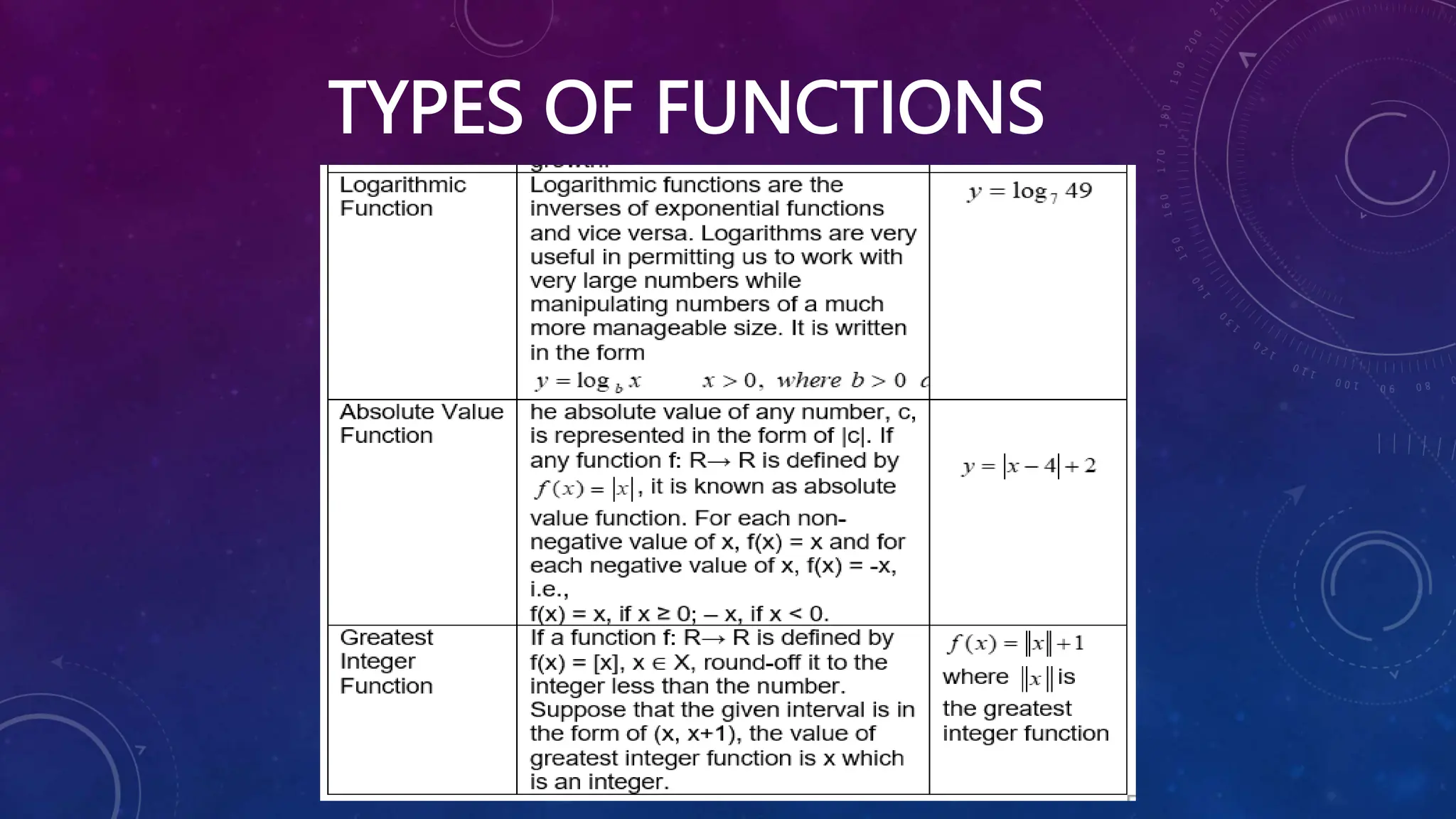
The document contains 9 multiple choice questions reviewing concepts related to functions such as identifying functions from relations, evaluating functions, performing operations on functions, and solving word problems involving functions. It also provides examples of representing real-life situations using functions and evaluating different types of functions.