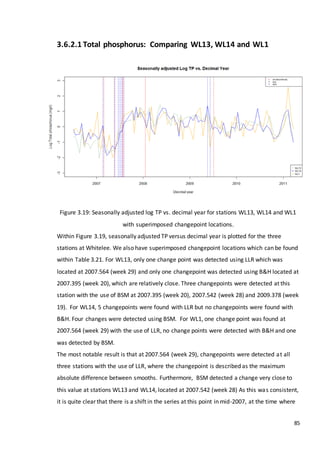
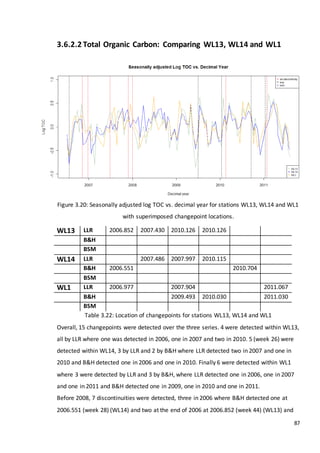
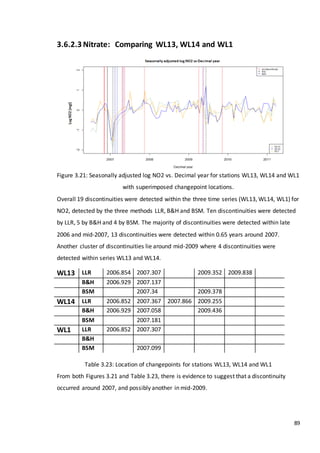
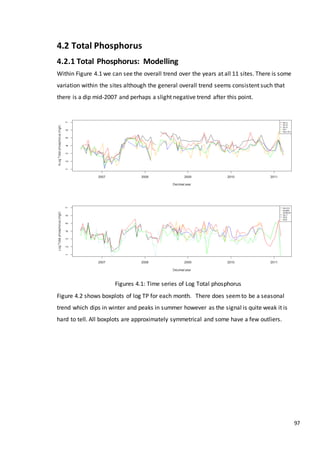
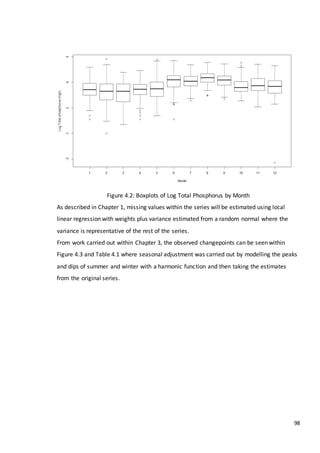
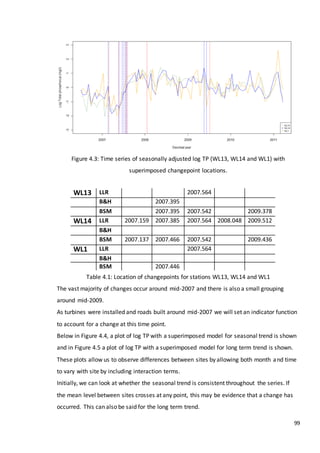
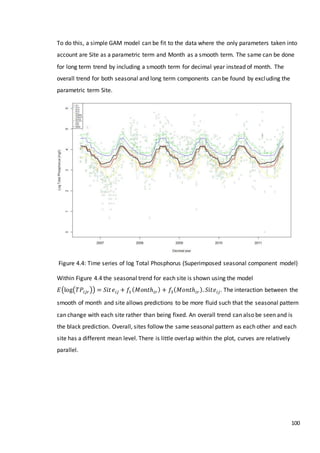
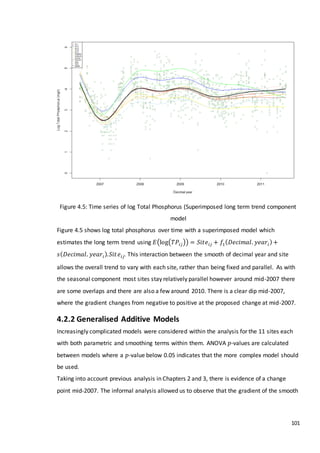
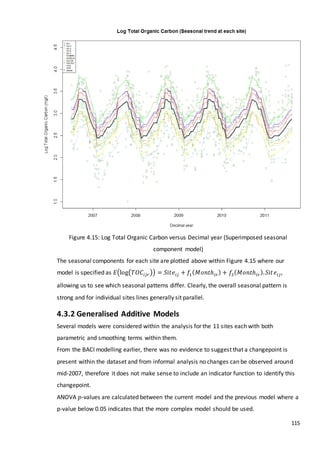
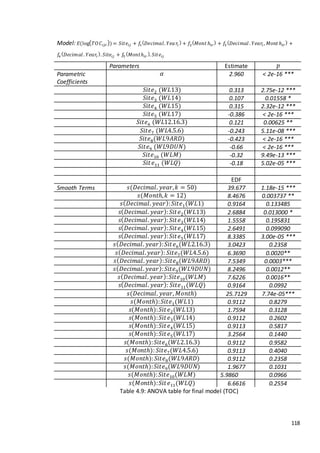
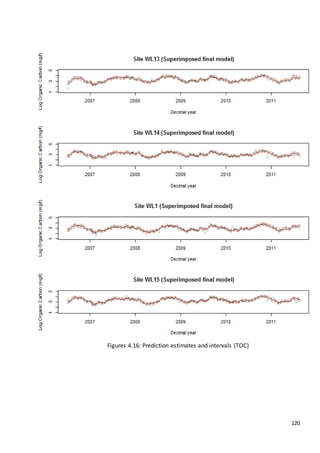
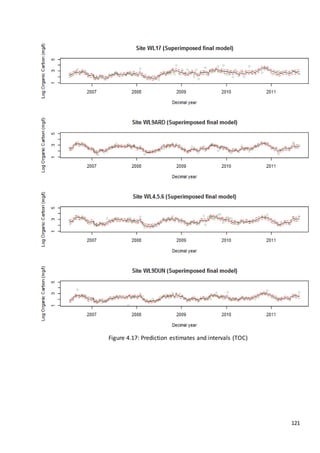
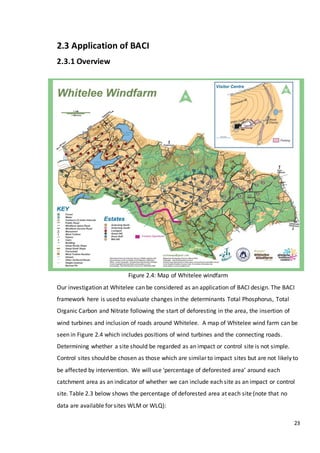
This document is a dissertation submitted by Fraser Tough to the University of Glasgow for the degree of Master of Science in May 2013. It examines the use of statistical methods for environmental impact assessment, including techniques to detect changes in time series data when the time of an intervention is known or unknown. The dissertation applies various statistical changepoint detection methods such as Before-After-Control-Impact design, local linear regression, and binary segmentation to real-world datasets on air pollution and water quality. The results are used to identify changes and better model trends over time in the datasets.
















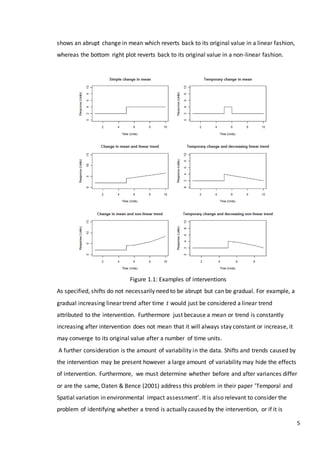


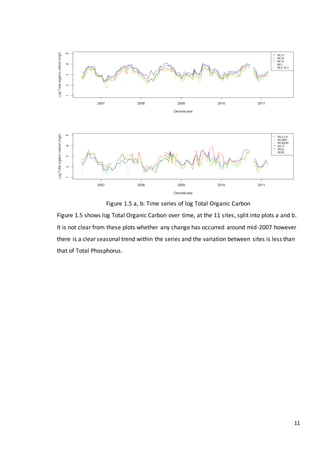









![25
Our observed errors 𝑒𝑖𝑗𝑘𝑟 are assumed to be normally distributed and independent with
zero mean and constant variance.
Our parameter Indicator (𝐼𝑖𝑘)has two levels, 0 and 1 (𝑘 = 0,1). The row vector is therefore
in the following form:
𝐼𝑖𝑘 = [0,… ,0,1, … ,1]
Where the changepoint is indicated by the change in value from 0 to 1.
The parameter Control/Impact (𝐶𝐼𝑖𝑟) is a row vector with two levels 𝐼 (impact) and 𝐶
(control) ( 𝑟 = 𝐼, 𝐶)and is in the following form:
𝐶𝐼𝑖𝑟 = [𝐶, … 𝐶, 𝐼, … 𝐼]
which indicates whether a site is a control site or an impact site.
The interaction 𝐼𝑖𝑘: 𝐶𝐼𝑖𝑟 allows us to determine whether there is a difference in the change
of mean before and after the changepoint between impact and control sites.
2.3.2 Total Phosphorus
2.3.2.1 Exploratory analysis (TP)
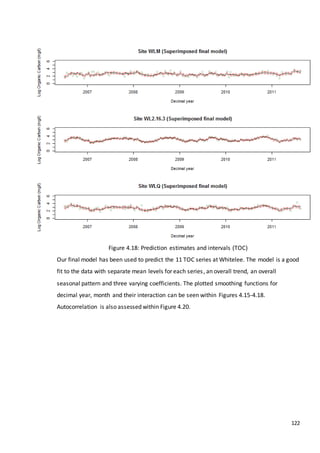
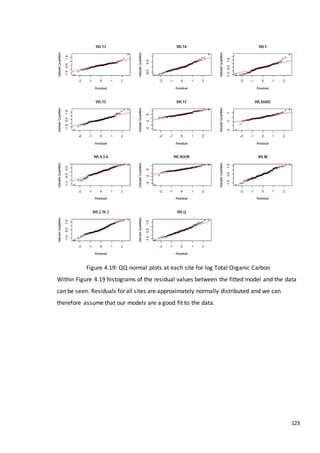
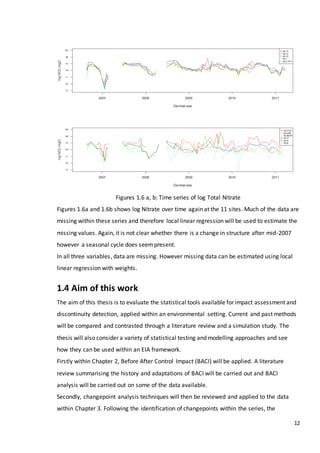
An initial impression of the data can be obtained by comparing mean values before and
after the intervention in mid-2007.
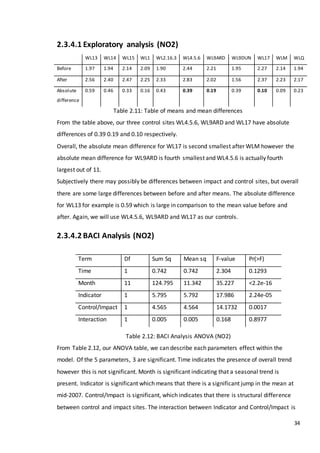
Shown below in Figure 2.3 are 11 boxplots. Within each there is one box-and-whisker for
before intervention and one after intervention. Table 2.4 also shows the mean before
intervention and the mean after at each site, as well as the absolute difference between the
two values. Absolute differences in bold are those sites that have a % deforested
of less than 2%.](https://image.slidesharecdn.com/8ecbc195-6b8d-4353-8d12-ac5e8964704e-170122130815/85/Fraser-Tough-MSc-thesis_FINAL-37-320.jpg)


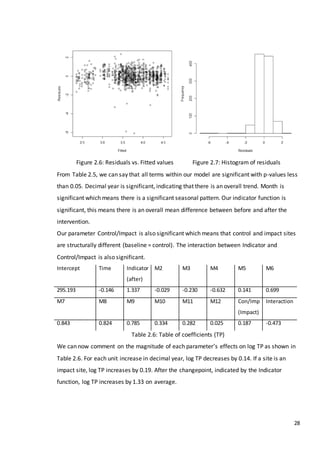

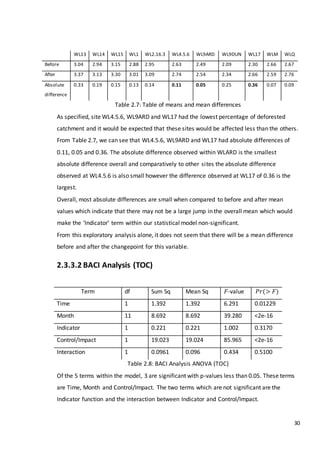


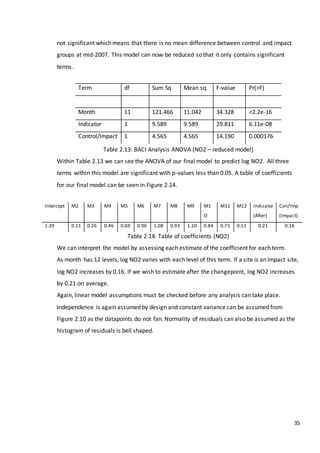









![46
method is effective in situations where there are not many changes ( 𝛾 𝑠𝑚𝑎𝑙𝑙) and where
the changes that do occur are of reasonable size ( 𝜆 𝑠𝑚𝑎𝑙𝑙). After each iteration the dataset
is updated conditional on the current partition.
No null or alternative hypothesis is specified within this framework but rather a probability
of a change point being present. Therefore, we must choose cut off points for probabilities
of change, which will be discussed in the next chapter.
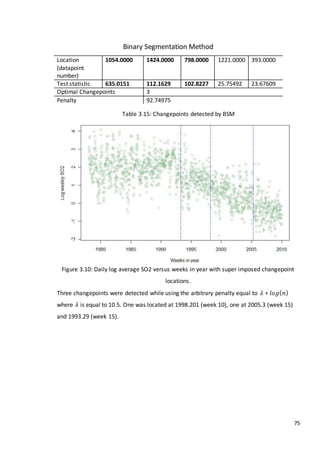
3.2.3 Binary Segmentation Method
Early applications of Binary Segmentation Method include Scott & Knott (1974) and Sen &
Srivastava (1975). This method uses two separate test statistics to determine if a change
point has occurred for both single and multiple changepoints.
Killick et al. (2012) developed an R package which allows users to apply BSM to time series
data.
For the single changepoint series, we consider a changepoint 𝜏1 .We will use a likelihood
ratio test statistic to determine whether there is a change in the series. The use of likelihood
ratio tests within changepoint analysis was first proposed by Hinkley (1970) and the test
statistic was firstly used to determine a change in the mean within normally distributed
data.
This method requires us to maximise the log likelihood value under both the null (no change
detected) and alternative hypotheses (change detected) where the maximum log-likelihood
value under the null hypothesis is log 𝑝(𝑦1:𝑛|𝜃̂) where 𝑝(.) is the PDF and 𝜃̂ is the MLE of
the parameters.
Under the alternative hypothesis we consider a model with changepoint at 𝜏1 where 𝜏1 can
take any value in the closed set (1,2,… . , 𝑛 − 1) then the maximum log likelihood for a given
𝜏1 is:
𝜆 = 2[𝑚𝑎𝑥𝑀𝐿( 𝜏1)− log 𝑝(𝑦1:𝑛|𝜃̂)] (3.8)
Such that we would reject 𝐻0 if 𝜆 > 𝑐 and then estimate the position of the changepoint
( 𝜏1̂ ) as the value of 𝜏1 that maximises 𝑀𝐿(𝜏1).
We can modify the single test to maximise 𝑀𝐿(𝜏1) over 𝑚 segments allowing us to
determine the location of multiple changepoints. The method requires us to minimise the
function:
∑ [𝐶(𝑦𝑚+1
𝑖=1 (𝜏𝑖−1 + 1) ∶ 𝜏𝑖 )] + 𝛽𝑓(𝑚) (3.9)](https://image.slidesharecdn.com/8ecbc195-6b8d-4353-8d12-ac5e8964704e-170122130815/85/Fraser-Tough-MSc-thesis_FINAL-58-320.jpg)
![47
Here 𝐶 is a cost function for a segment and 𝛽𝑓(𝑚) is a penalty to guard against over fitting.
Using notation from the single changepoint section, 𝐶 may be taken as the negative log
likelihood and 𝛽𝑓(𝑚) may be 𝑐𝑚.
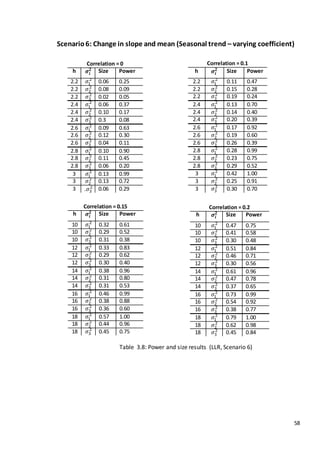
The algorithm shown below applies the single changepoint test and upon identifying a
change, iteratively implements the test statistic on the sub-segments of the data developed
by Killick et al. (2012).
Input: A set of data of the form (𝑦1, 𝑦2 , … , 𝑦 𝑛)
A test statistic 𝜆(. ) dependent on the data
An estimator of changepoint position 𝜏(. )
A rejection threshold (penalty), 𝑐
Initialise: Let 𝐶 = 𝜙 and 𝑆 = {[1, 𝑛]}
Iterate while 𝑆 ≠ 𝜙
1. Choose an element of 𝑆; denote this element as [ 𝑠, 𝑡].
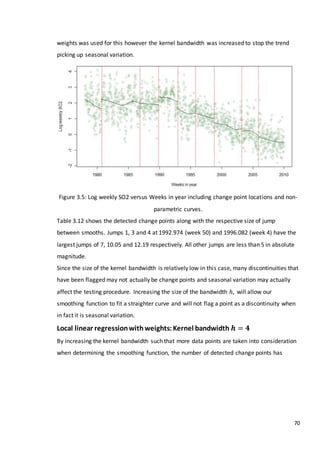
2. If 𝜆( 𝑦𝑠:𝑡) < 𝑐 remove [𝑠, 𝑡] from 𝑆.
3. If 𝜆( 𝑦𝑠:𝑡) ≥ 𝑐 then;
(a) remove [ 𝑠, 𝑡] from 𝑆
(b) calculate 𝜏 = 𝜏̂( 𝑦𝑠:𝑡) + 𝑠 − 1, and add 𝜏 to 𝐶;
(c) if 𝜏 ≠ 𝑠 add [ 𝑠, 𝜏] to 𝑆
(d) if 𝜏 ≠ 𝑡 − 1 add [ 𝜏 + 1, 𝑡]to 𝑆
Output the set of changepoints recorded 𝐶
(TakenfromKillicketal.(2012))
In essence the method extends a single changepoint method to multiple changepoints by
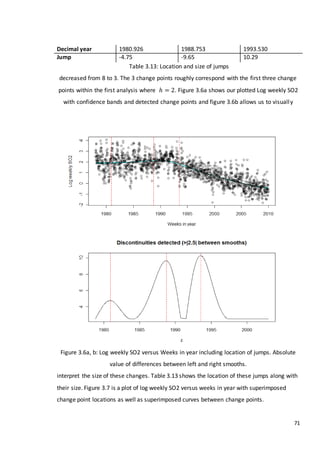
repeating the method on varying subsets of the series iteratively:
The penalty can take any value, however Killick et al. (2012) uses 𝜆 ∗ 𝑙𝑜𝑔(𝑛) where 𝑛 is the
number of observations within the series and 𝜆 can be arbitrarily changed depending on the
expected size of the change.
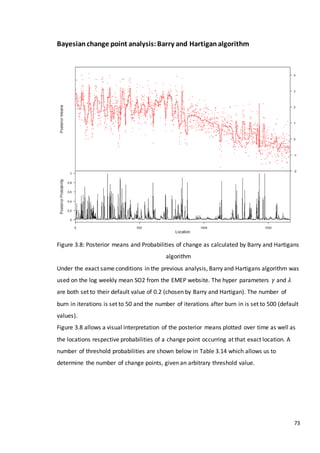
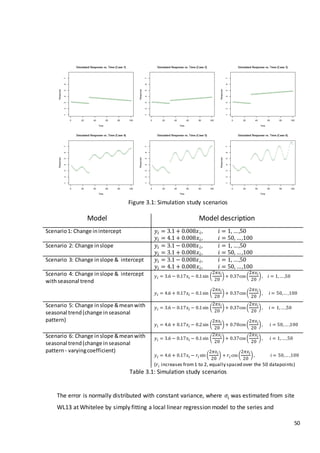
3.3 Simulation study
In this section we will consider how various tests perform at detecting a discontinuity within
a time series. We wish to determine the effects of changing shape and trend in the series](https://image.slidesharecdn.com/8ecbc195-6b8d-4353-8d12-ac5e8964704e-170122130815/85/Fraser-Tough-MSc-thesis_FINAL-59-320.jpg)



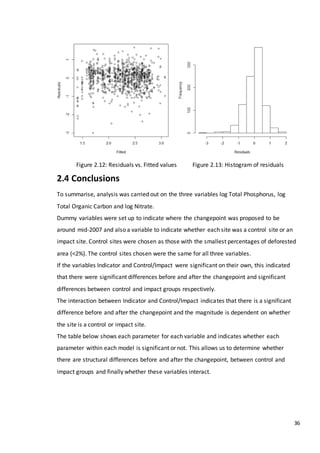
![52
also be under smoothed leaving a hidden function within the data, resulting in a higher
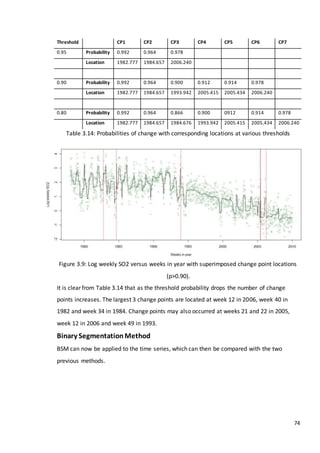
estimate of the correlation.
From preliminary analysis we know that we do not have any significant autocorrelation, the
covariance matrix is simply an 𝐴𝑅(1)as shown below:
Σ =
[
1 𝛼 𝛼2
⋯ 𝛼 𝑛−1
𝛼 1 𝛼 ⋯ 𝛼 𝑛−2
𝛼2
𝛼 1 ⋯ 𝛼 𝑛−3
⋮ ⋮ ⋮ ⋱ ⋮
𝛼 𝑛−1
𝛼 𝑛−2
𝛼 𝑛−3
⋯ 1 ]
If the true value of 𝛼 is not known, we must obtain 𝛼̂, our estimate of the correlation, to
obtain Σ̂.
The smoothing parameter, which in this case is the kernel bandwidth of the weights must
also be chosen when carrying out this test. This is denoted as ℎ. This parameter determines
the standard deviation of the kernel, which is a normal probability distribution. This means
that points that lie close to the point of interest will have more of an influence than points
lying farther away. For scenarios 4-6, smaller values of ℎ will be used since the data has a
seasonal cycle. The smaller bandwidth allows the smoothed curve to follow the data more
closely since points that are father away, and therefore less likely to have a relationship with
the point of interest, will have less influence on the smoothed curve.
To determine each tests power we have chosen a range of bandwidths to asses. The choices
represent small moderate and large amounts of smoothing for the regression.
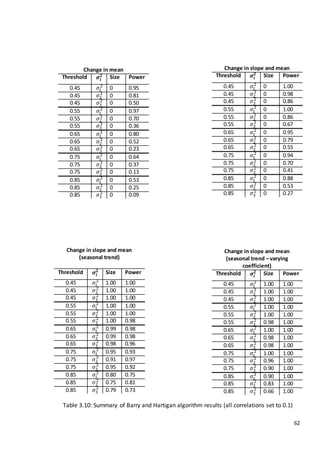
The simulated data will have the following characteristics:
Model and data conditions
Data spacing
Numberof simulations
Lengthof time series
Equallyspaced
100
100
Varying parameters
Error
Correlation
Kernel Bandwidth
𝜖~𝑁(0, 𝜎2Σ) , 𝜎= 0.35, 0.50, 0.65
𝜌=0.1, 0.15, 0.2
ℎ = 10,12, 14, 16,18
Table 3.2: Simulation conditions
Where within each case, various correlation coefficients, errors and smoothing parameters
will be used.](https://image.slidesharecdn.com/8ecbc195-6b8d-4353-8d12-ac5e8964704e-170122130815/85/Fraser-Tough-MSc-thesis_FINAL-64-320.jpg)