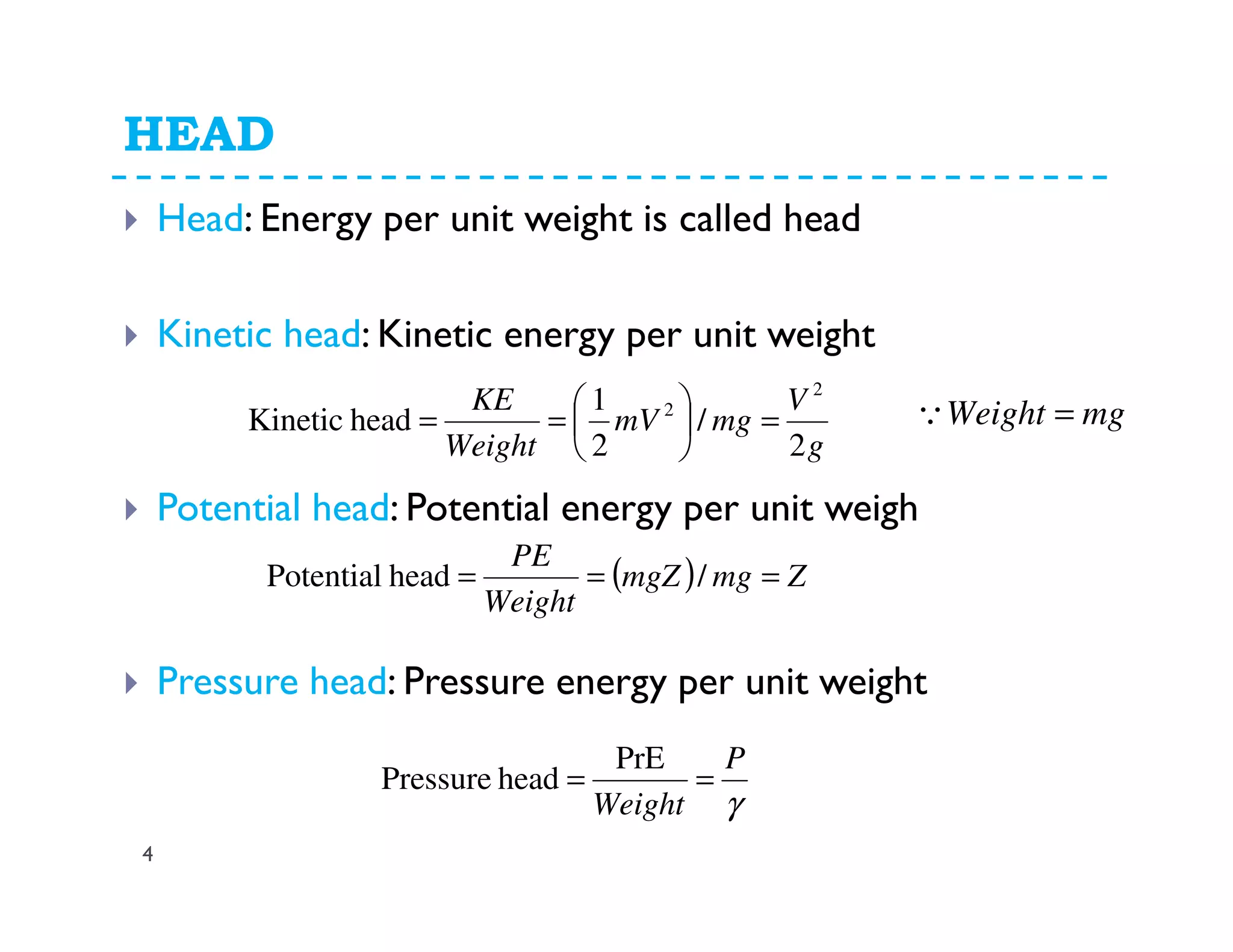
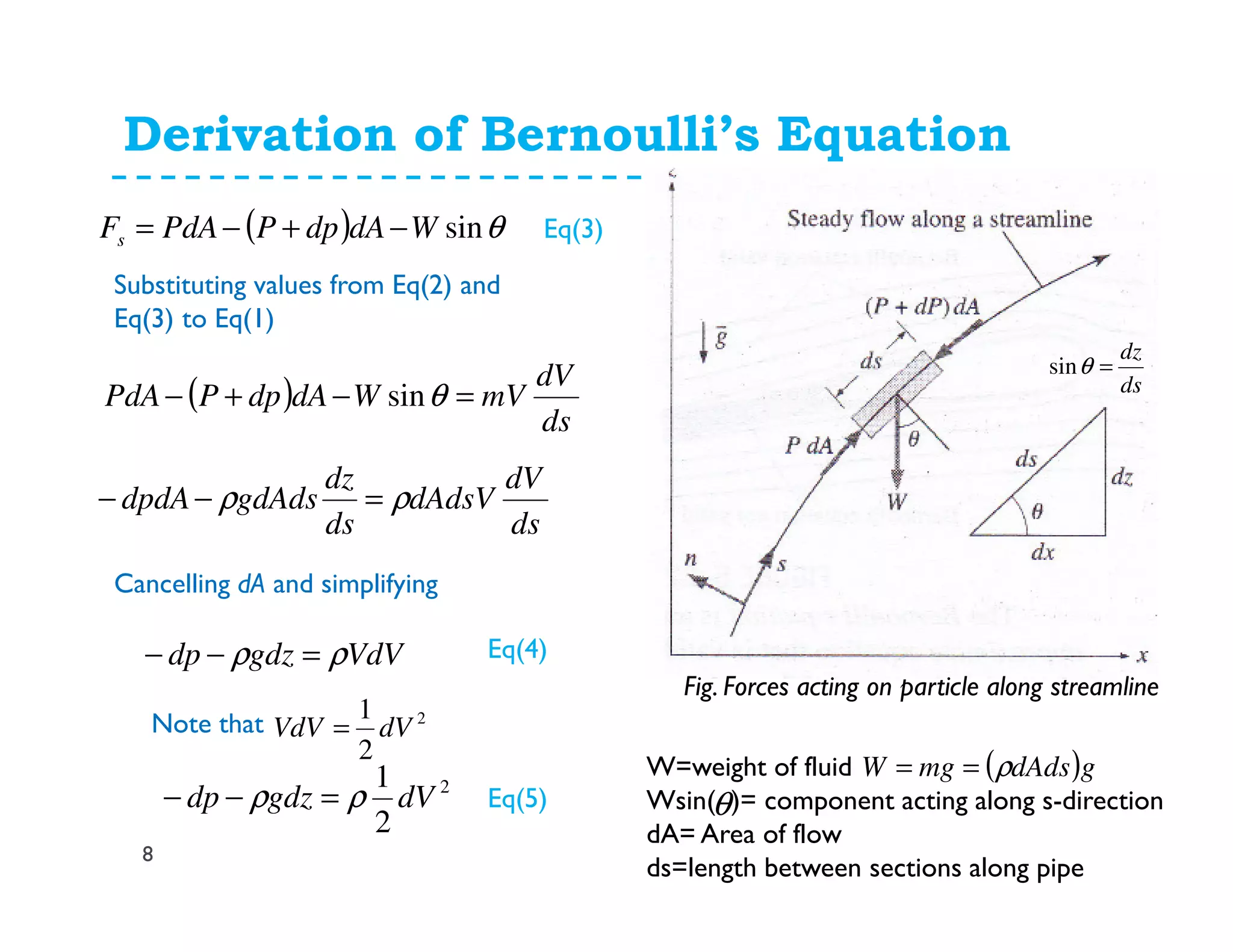
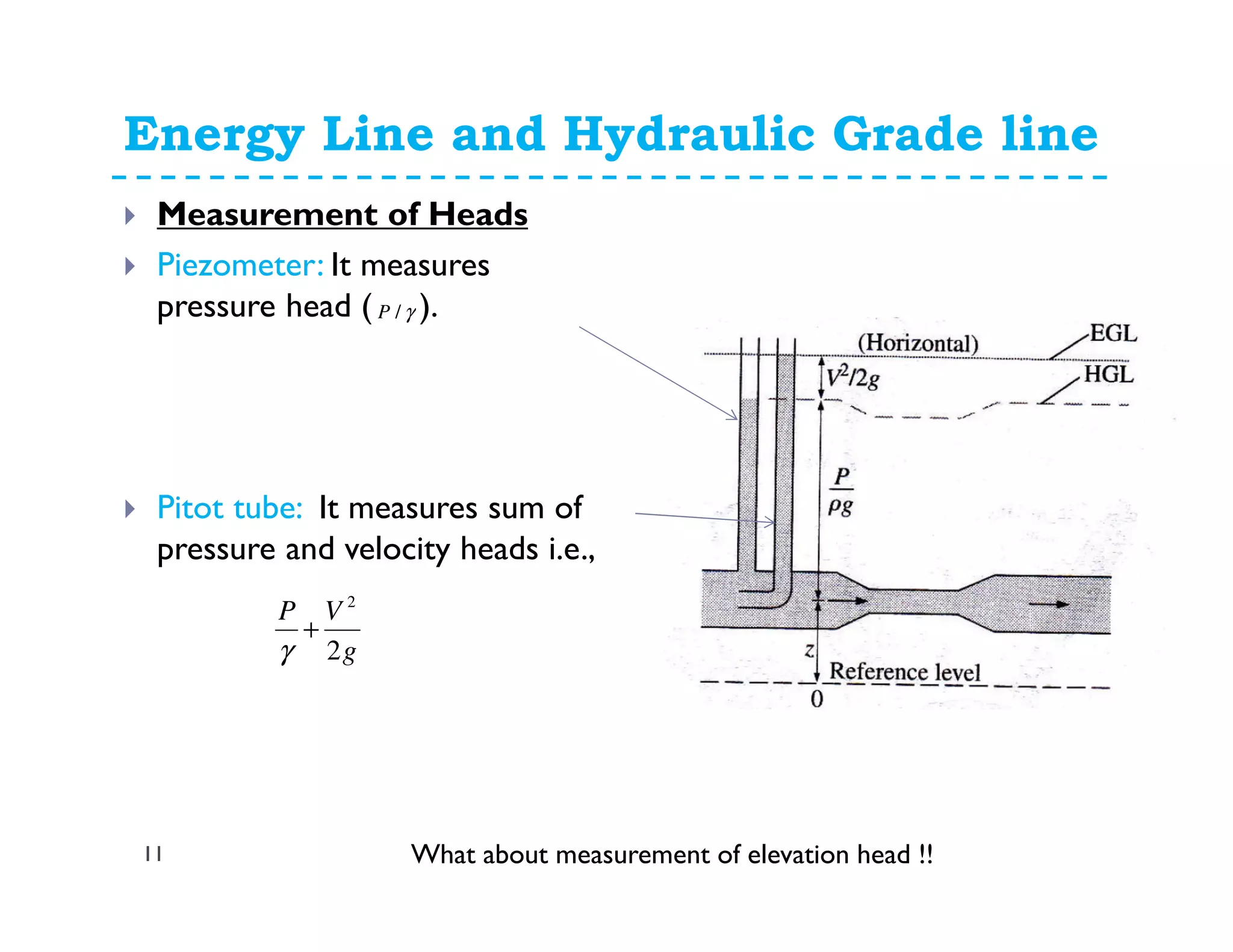
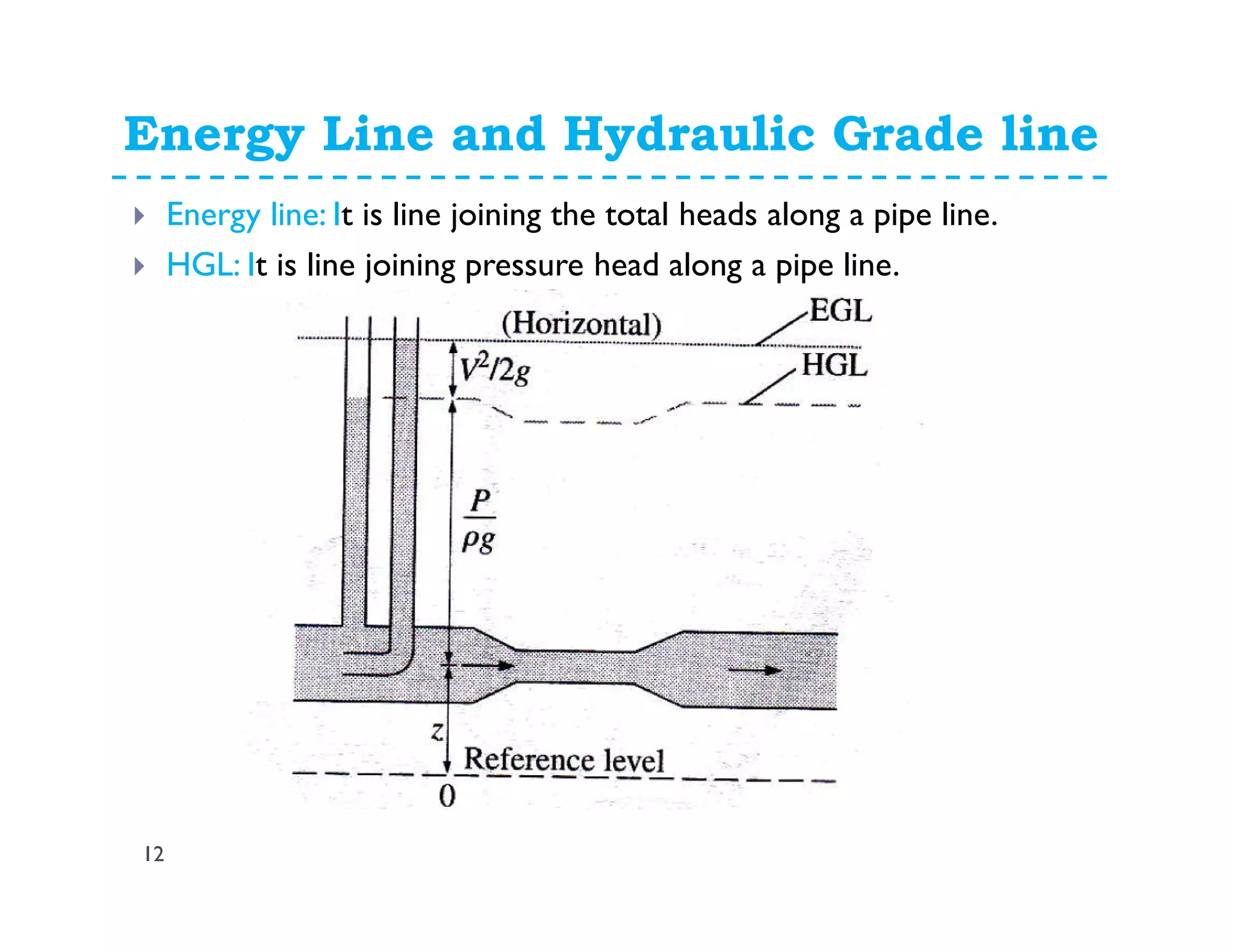
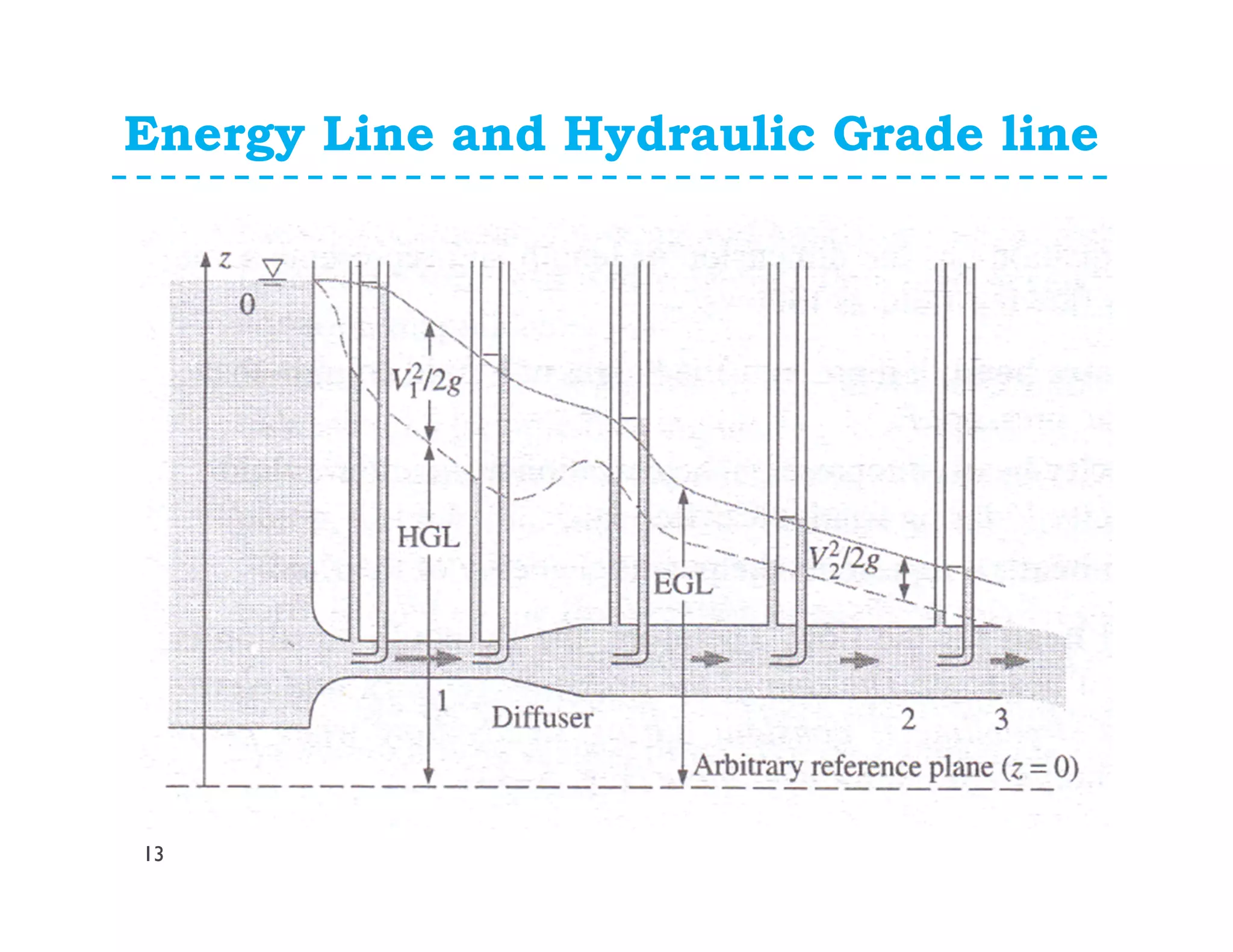
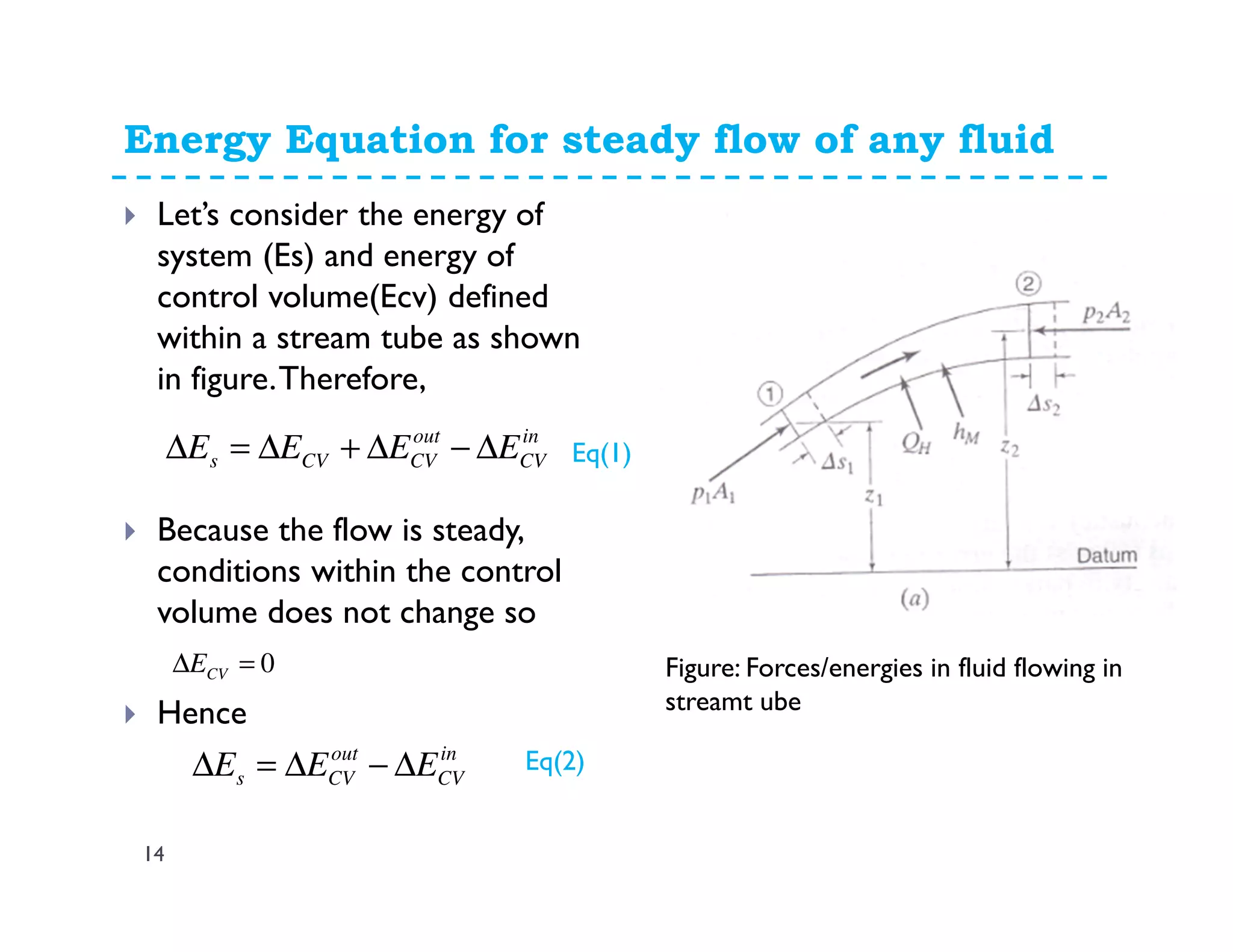
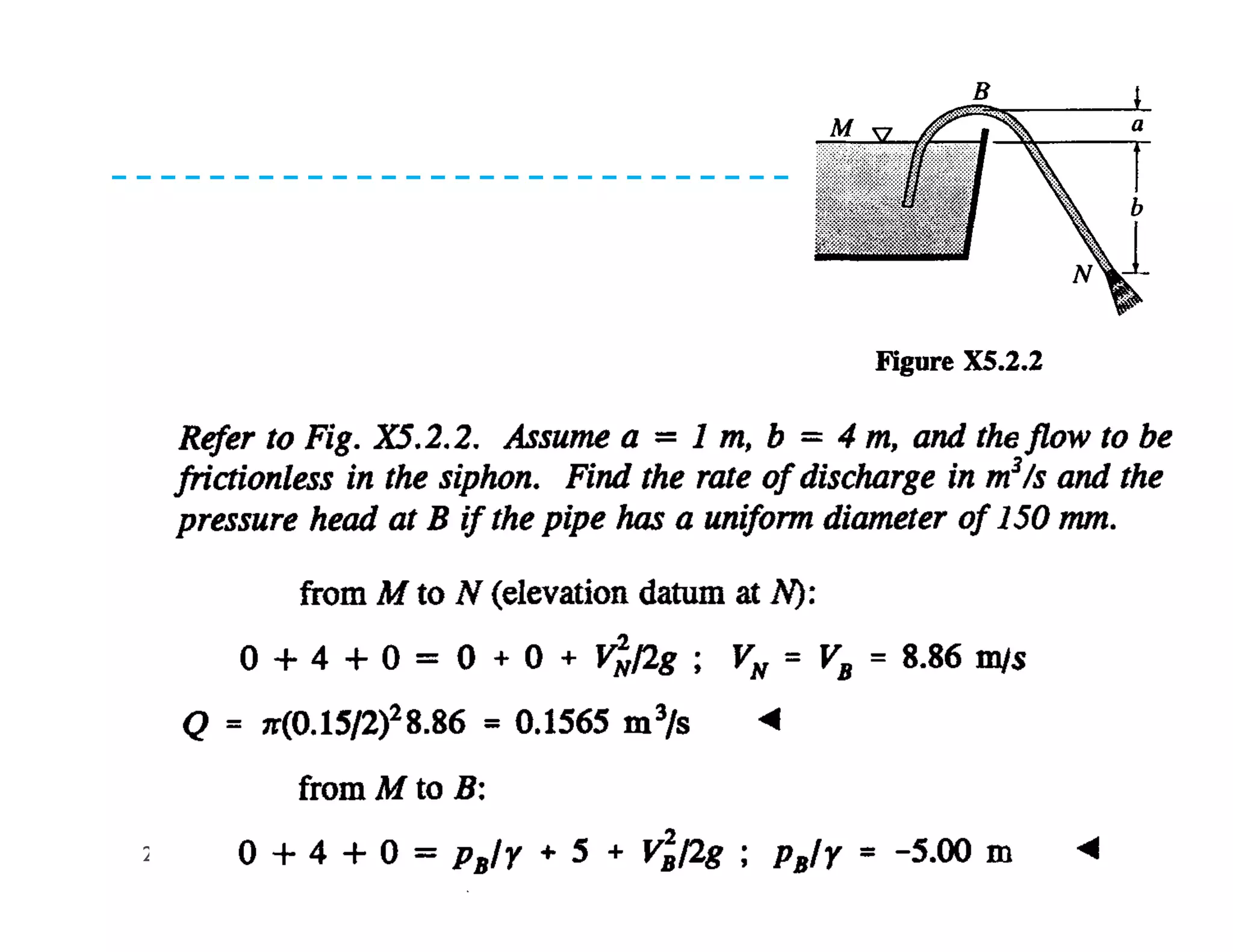
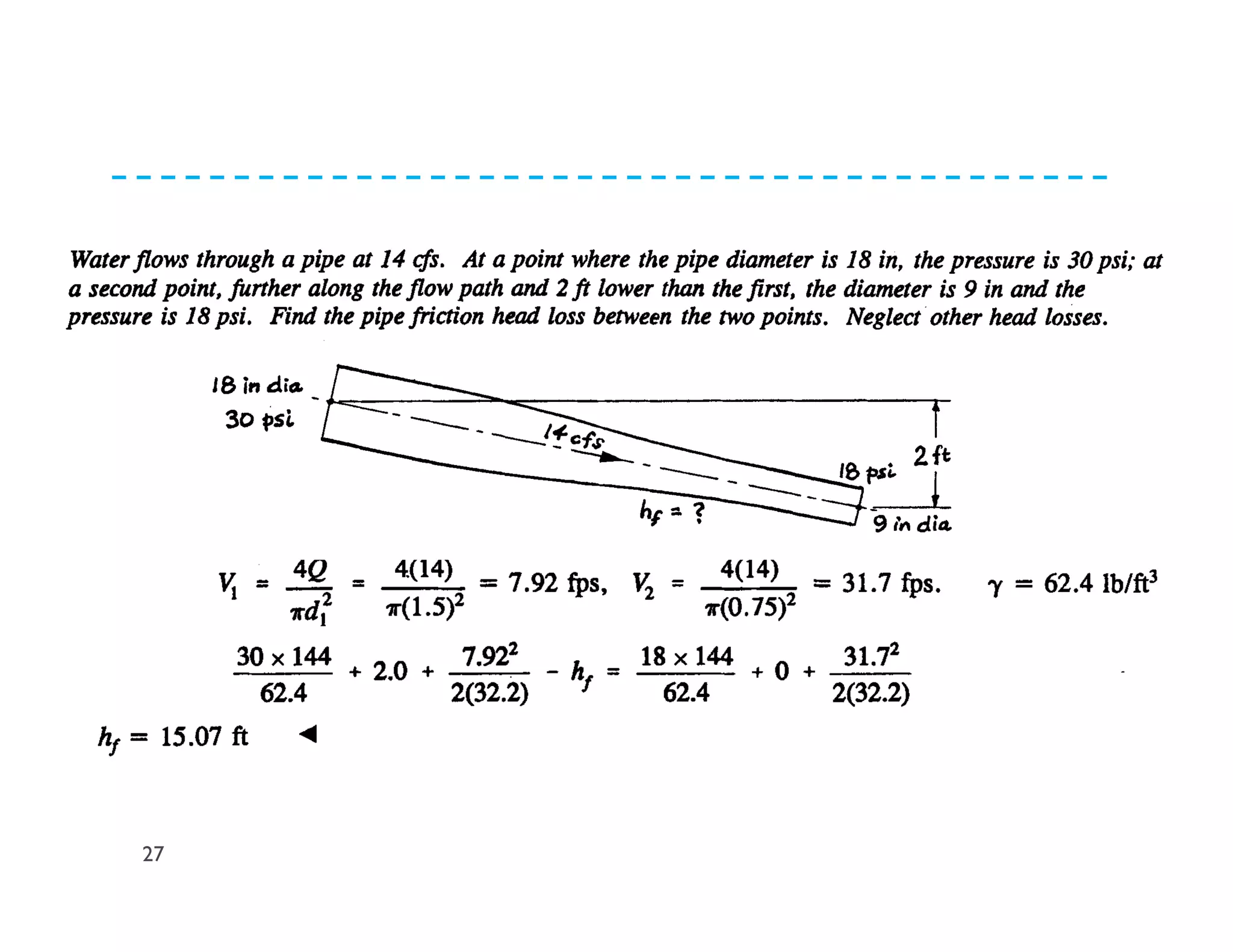
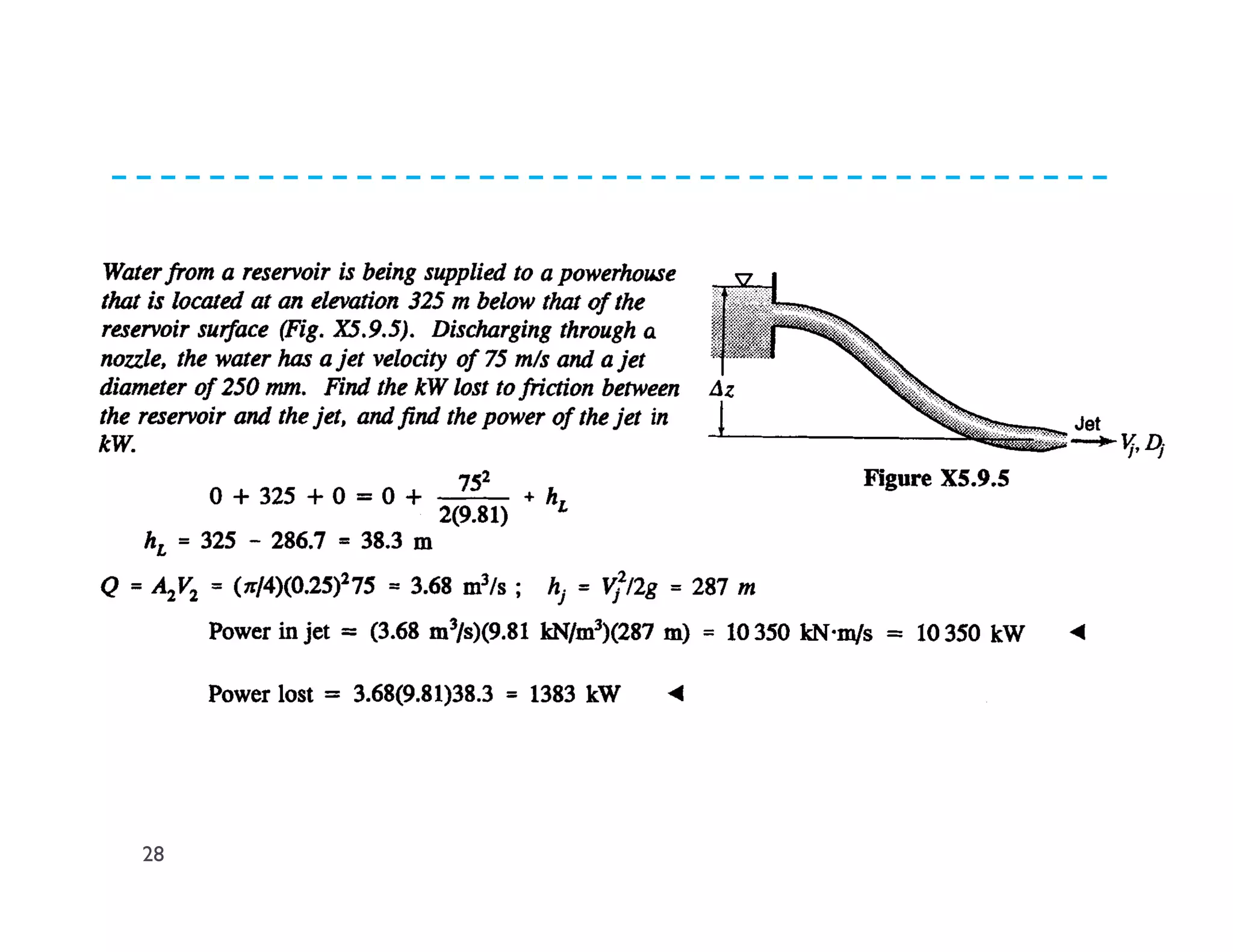
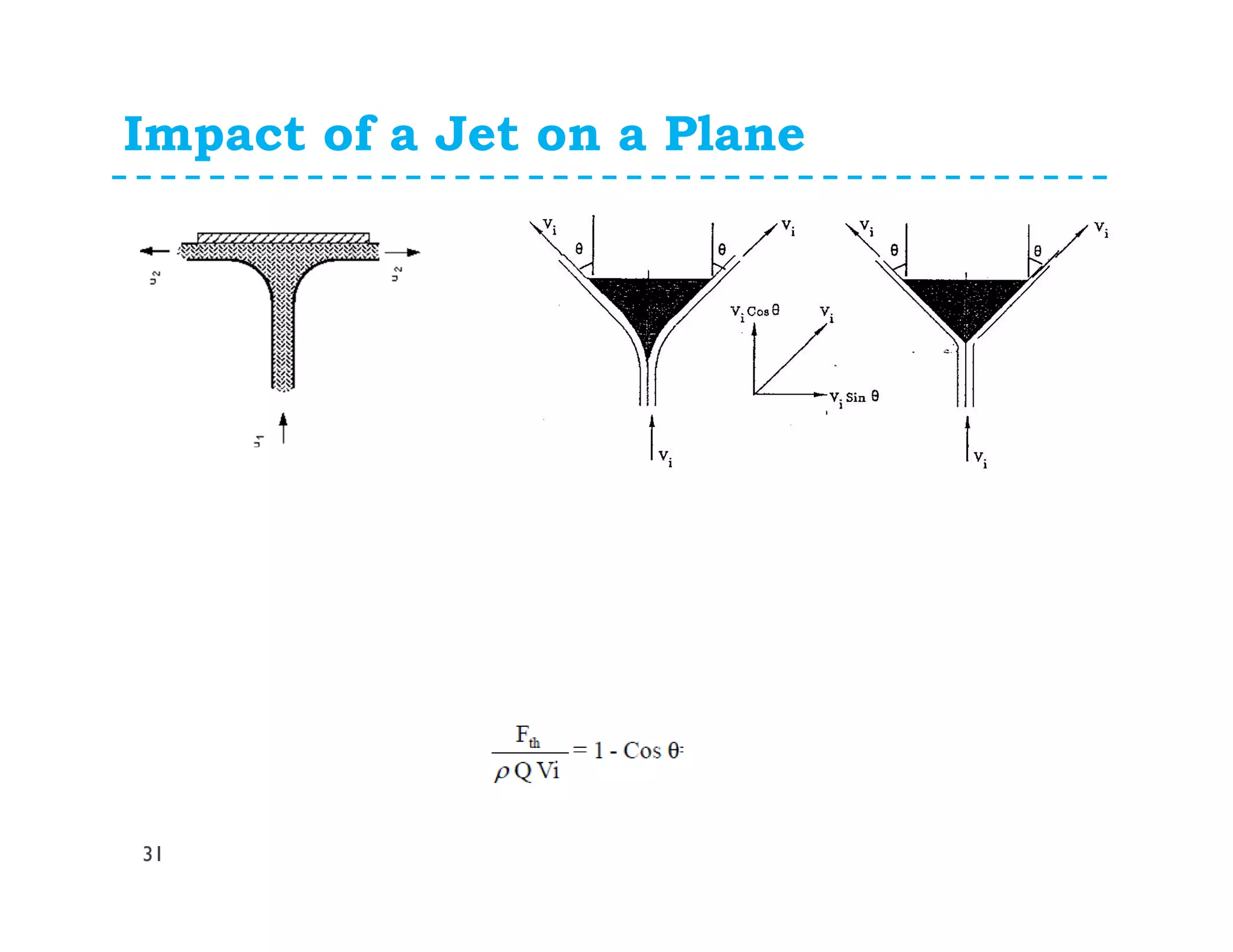
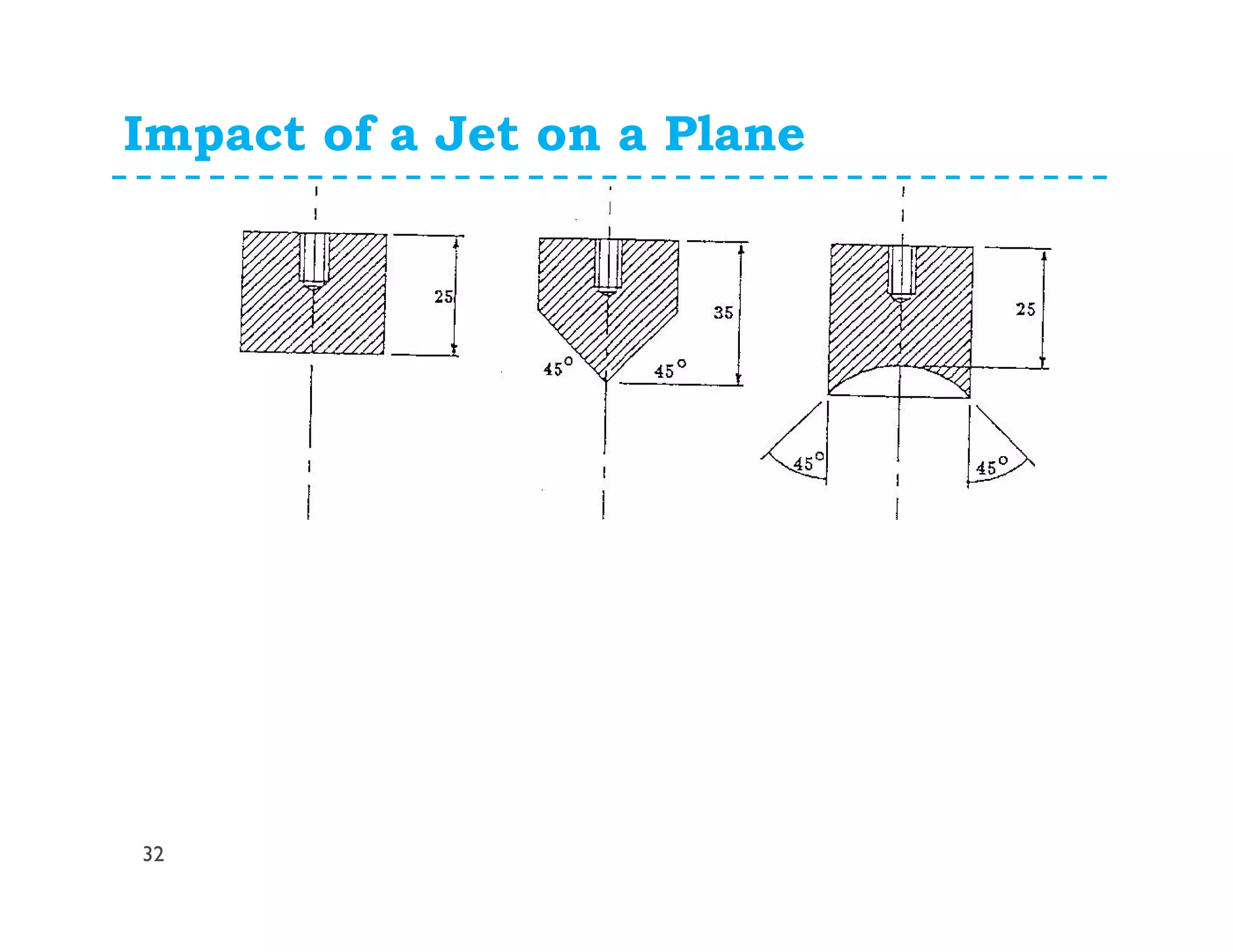
This document discusses fluid dynamics and Bernoulli's equation. It begins by defining different forms of energy in a flowing liquid, including kinetic energy, potential energy, pressure energy, and internal energy. It then derives Bernoulli's equation, which states that the total head of a fluid particle remains constant during steady, incompressible flow. The derivation considers forces acting on a fluid particle and uses conservation of energy. Finally, the document presents the general energy equation for steady fluid flow and the specific equation for incompressible fluids using the concepts of total head, head loss, and hydraulic grade line.

1. Fluid Dynamics:
(ii) Hydrodynamics: Different forms of energy in a flowing
liquid, head, Bernoulli's equation and its application, Energy
line and Hydraulic Gradient Line, and Energy Equation
Dr. Mohsin Siddique
Assistant Professor
1
Fluid Mechanics

2. Forms of Energy
2
(1). Kinetic Energy: Energy due to motion of body.A body of
mass, m, when moving with velocity, V, posses kinetic energy,
(2). Potential Energy: Energy due to elevation of body above an
arbitrary datum
(3). Pressure Energy: Energy due to pressure above datum, most
usually its pressure above atmospheric
2
2
1
mVKE =
mgZPE =
m andV are mass and velocity of body
Z is elevation of body from arbitrary datum
m is the mass of body
hγ=PrE !!!

3. Forms of Energy
3
(4). Internal Energy: It is the energy that is associated with the
molecular, or internal state of matter; it may be stored in many
forms, including thermal, nuclear, chemical and electrostatic.

4. HEAD
4
Head: Energy per unit weight is called head
Kinetic head: Kinetic energy per unit weight
Potential head: Potential energy per unit weigh
Pressure head: Pressure energy per unit weight
g
V
mgmV
Weight
KE
2
/
2
1
headKinetic
2
2
=





== mgWeight =Q
( ) ZmgmgZ
Weight
PE
=== /headPotential
γ
P
Weight
==
PrE
headPressure

5. TOTAL HEAD
5
TOTAL HEAD
= Kinetic Head + Potential Head + Pressure Head
g
VP
Z
2
HHeadTotal
2
++==
γ
g
V
2
2
γ
P
Z

6. Bernoulli’s Equation
6
It states that the sum of kinetic, potential and pressure heads
of a fluid particle is constant along a streamline during steady
flow when compressibility and frictional effects are negligible.
i.e. , For an ideal fluid,Total head of fluid particle remains
constant during a steady-incompressible flow.
Or total head along a streamline is constant during steady flow
when compressibility and frictional effects are negligible.
21
2
2
2
2
1
2
1
1
2
22
2
HeadTotal
HH
g
VP
Z
g
VP
Z
constt
g
VP
Z
=
++=++
=++=
γγ
γ
1
2
Pipe

7. Derivation of Bernoulli’s Equation
7
Consider motion of flow fluid
particle in steady flow field as
shown in fig.
Applying Newton’s 2nd Law in s-
direction on a particle moving
along a streamline give
Where F is resultant force in s-
direction, m is the mass and as is
the acceleration along s-direction.
ss maF =
Assumption:
Fluid is ideal and incompressible
Flow is steady
Flow is along streamline
Velocity is uniform across the section and is equal
to mean velocity
Only gravity and pressure forces are acting
ds
dV
V
dtds
dsdV
dsdt
dsdV
dt
dV
as ====
Eq(1)
Eq(2)
Fig. Forces acting on particle along streamline

8. Derivation of Bernoulli’s Equation
8
W=weight of fluid
Wsin( )= component acting along s-direction
dA= Area of flow
ds=length between sections along pipe
θ
( ) θsinWdAdpPPdAFs −+−=
Substituting values from Eq(2) and
Eq(3) to Eq(1)
Eq(3)
( )
ds
dV
mVWdAdpPPdA =−+− θsin
ds
dV
dAdsV
ds
dz
gdAdsdpdA ρρ =−−
( )gdAdsmgW ρ==
ds
dz
=θsin
Cancelling dA and simplifying
VdVgdzdp ρρ =−−
Note that 2
2
1
dVVdV =
2
2
1
dVgdzdp ρρ =−−
Eq(4)
Eq(5)
Fig. Forces acting on particle along streamline

9. Derivation of Bernoulli’s Equation
9
Dividing eq (5) by
Integrating
Assuming incompressible and
steady flow
Dividing each equation by g
ρ
0
2
1 2
=++ dVgdz
dp
ρ
conttdVgdz
dp
=





++∫
2
2
1
ρ
conttVgz
P
=++ 2
2
1
ρ
contt
g
V
z
g
P
=++
2
2
ρ
Hence Eq (9) for stead-
incompressible fluid assuming no
frictional losses can be written as
Eq (6)
Eq (7)
Eq (8)
Eq (9)
( ) ( )21
2
2
2
2
1
2
1
1
HeadTotalHeadTotal
22
=
++=++
g
VP
Z
g
VP
Z
γγ
Above Eq(10) is general form of
Bernoulli’s Equation
Eq (10)

10. Energy Line and Hydraulic Grade line
10
Static Pressure :
Dynamic pressure :
Hydrostatic Pressure:
Stagnation Pressure: Static pressure + dynamic Pressure
H
g
V
z
P
=++
2
2
γ
HeadTotalheadVelocityheadElevationheadPressure =++
P
gZρ
2/2
Vρ
contt
V
gzP =++
2
2
ρρ
Multiplying with unit weight,γ,
stagP
V
P =+
2
2
ρ

11. Energy Line and Hydraulic Grade line
11
Measurement of Heads
Piezometer: It measures
pressure head ( ).
Pitot tube: It measures sum of
pressure and velocity heads i.e.,
g
VP
2
2
+
γ
γ/P
What about measurement of elevation head !!

12. Energy Line and Hydraulic Grade line
12
Energy line: It is line joining the total heads along a pipe line.
HGL: It is line joining pressure head along a pipe line.

13. Energy Line and Hydraulic Grade line
13

14. Energy Equation for steady flow of any fluid
14
Let’s consider the energy of
system (Es) and energy of
control volume(Ecv) defined
within a stream tube as shown
in figure.Therefore,
Because the flow is steady,
conditions within the control
volume does not change so
Hence
in
CV
out
CVCVs EEEE ∆−∆+∆=∆
in
CV
out
CVs EEE ∆−∆=∆
0=∆ CVE
Eq(1)
Eq(2)
Figure: Forces/energies in fluid flowing in
streamt ube

15. Energy Equation for steady flow of any
fluid
15
Now, let’s apply the first law of thermodynamics to the fluid system
which states ” For steady flow, the external work done on any system
plus the thermal energy transferred into or out of the system is equal to
the change of energy of system”
( )
( ) in
CV
out
CV
s
EEshaftworklowwork
Eshaftworklowwork
∆−∆=++
∆=++
=+
ferredheat transf
ferredheat transf
energyofchangeferredheat transdoneworkExternal
Flow work: When the pressure forces acting on the boundaries
move, in present case when p1A1 and p2A2 at the end sections move
through ∆s1 and ∆s2, external work is done. It is referred to as flow
work.
msAsA
pp
mg
sA
p
sA
p
sApsAp
∆=∆=∆





−∆=
∆−∆=∆−∆=
222111
2
2
1
1
222
2
2
111
1
1
111111
workFlow
workFlow
ρρ
γγ
γ
γ
γ
γ
Q Steady flow
Eq(3)
Eq(4)
Eq(5)

16. Energy Equation for steady flow of any
fluid
16
Shaft work: Work done by machine, if any, between section 1 and 2
( ) ( ) mm
m
hmghsA
th
dt
ds
Atime
weight
energy
time
weight
∆=∆=
∆





==
111
1
11
Shaft work
Shaft work
γ
γ
Where, hm is the energy added to the flow by the machine per unit
weight of flowing fluid. Note: if the machine is pump, which adds energy
to the fluid, hm is positive and if the machine is turbine, which remove
energy from fluid, hm is -ve
HeatTransferred: The heat transferred from an external source
into the fluid system over time interval ∆t is
( ) ( ) HH
H
QmgQsA
tQ
dt
ds
A
∆=∆=
∆





=
111
1
11
ferredHeat trans
ferredHeat trans
γ
γ
Where, QH is the amount of energy put into the flow by the external
heat source per unit weight of flowing fluid. If the heat flow is out of the
fluid, the value QH is –ve and vice versa
Eq(6)
Eq(7)

17. Energy Equation for steady flow of any
fluid
17
Change in Energy: For steady flow during time interval ∆t, the weight of
fluid entering the control volume at section 1 and leaving at section 2 are
both equal to g∆m .Thus the energy (Potential+Kinetic+Internal) carried by
g∆m is;
( )
( )






++∆=∆






++=∆





++





=∆






++∆=∆






++=∆





++





=∆
2
2
2
2
2
2
2
22222
2
2
2
2
22
1
2
1
1
1
2
1
11111
2
1
1
1
11
2
22
2
22
I
g
V
zmgE
I
g
V
zdsAtI
g
V
z
dt
ds
AE
I
g
V
zmgE
I
g
V
zdsAtI
g
V
z
dt
ds
AE
out
CV
out
CV
in
CV
in
CV
α
αγαγ
α
αγαγ
α is kinetic energy correction factor and ~ 1
Eq(8)
Eq(9)

18. Energy Equation for steady flow of any
fluid
18
Substituting all values from Eqs. (5),(6), (7), (8), & (9) in Eq(4)
( ) in
CV
out
CV EEshaftworklowwork ∆−∆=++ ferredheat transf
( ) ( ) 





++∆−





++∆=∆+∆+





−∆ 1
2
1
12
2
2
2
2
2
1
1
22
I
g
V
zmgI
g
V
zmgQmghmg
pp
mg Hm αα
γγ






++−





++=++





− 1
2
1
12
2
2
2
2
2
1
1
22
I
g
V
zI
g
V
zQh
pp
Hm αα
γγ






+++=++





++− 2
2
2
2
2
2
1
2
1
1
1
1
22
I
g
V
z
p
QhI
g
V
z
p
Hm α
γ
α
γ
This is general form of energy equation, which applies to liquids, gases, vapors
and to ideal fluids as well as real fluids with friction, both incompressible and
compressible.The only restriction is that its for steady flow.
Eq(10)

19. Energy Equation for steady flow of
incompressible fluid
19
For incompressible fluids
Substituting in Eq(10), we get
( )12
2
2
2
2
2
1
1
1
22
II
g
V
z
p
Qh
g
V
z
p
Hm −+





++=++





+−
γγ
γγγ == 21
( ) Hm QII
g
V
z
p
h
g
V
z
p
−−+





++=+





+− 12
2
2
2
2
2
1
1
1
22 γγ
Lm h
g
V
z
p
h
g
V
z
p
+





++=+





+−
22
2
2
2
2
2
1
1
1
γγ Eq(11)
( ) HL QIIh −−= 12Q
Where hL=(I2-I1)-QH= head loss. It equal to is gain in internal energy minus
any heat added by external source.
Hm is head removed/added by machines. It can also be referred to head loss
due to pipe fitting, contraction, expansion and bends etc in pipes.

20. Energy Equation for steady flow of
incompressible fluid
20
In the absence of machine, pipe fitting etc, Eq(11) can be written as
When the head loss is caused only by wall or pipe friction, hL
becomes hf, where hf is head loss due to friction
Lh
g
V
z
p
g
V
z
p
+








++=








++
22
2
2
2
2
2
1
1
1
γγ Eq(12)

21. Power
21
Rate of work done is termed as power
Power=Energy/time
Power=(Energy/weight)(weight/time)
If H is total head=total energy/weight and γQ is the weight flow rate
then above equation can be written as
Power=(H)(γQ)= γQH
In BG:
Power in (horsepower)=(H)(γQ)/550
In SI:
Power in (Kilowatts)=(H)(γQ)/1000
1 horsepower=550ft.lb/s

22. Reading Assignment
22
Kinetic energy correction factor
Limitation of Bernoulli’s Equation
Application of hydraulic grade line and energy line

23. NUMERICALS
23
5.2.1

24. 24
5.2.3

25. 25
5.3.2

26. 26
5.3.4

27. 27
5.3.6

28. 28
5.9.6

29. Momentum and Forces in Fluid Flow
29
We have all seen moving fluids exerting forces.The lift force on an aircraft
is exerted by the air moving over the wing. A jet of water from a hose
exerts a force on whatever it hits.
In fluid mechanics the analysis of motion is performed in the same way as in
solid mechanics - by use of Newton’s laws of motion.
i.e., F = ma which is used in the analysis of solid mechanics to relate applied
force to acceleration.
In fluid mechanics it is not clear what mass of moving fluid we should use
so we use a different form of the equation.
( )
dt
md
ma sV
F ==∑

30. Momentum and Forces in Fluid Flow
30
Newton’s 2nd Law can be written:
The Rate of change of momentum of a body is equal to the resultant force acting
on the body, and takes place in the direction of the force.
The symbols F and V represent vectors and so the change in momentum must be
in the same direction as force.
It is also termed as impulse momentum principle
( )
dt
md sV
F =∑
=
=∑
mV
F Sum of all external forces on a body of fluid or system s
Momentum of fluid body in direction s
( )smddt VF =∑

31. Impact of a Jet on a Plane
31

32. Impact of a Jet on a Plane
32

33. Thank you
Questions….
Feel free to contact:
33