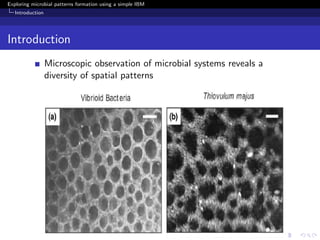
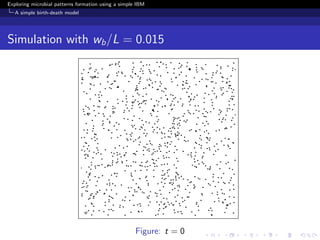
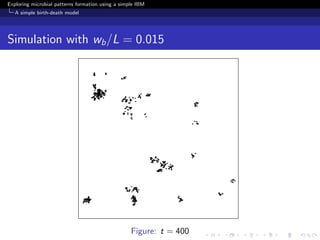
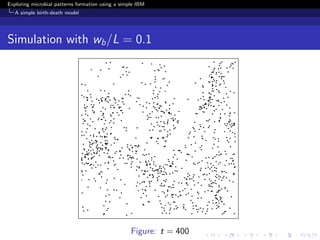
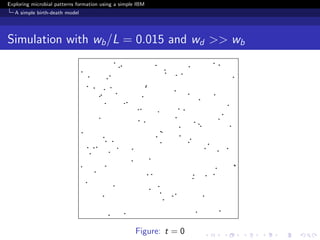
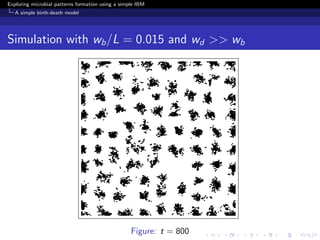
The document investigates the formation of microbial patterns using an individual-based modeling approach, specifically through a simple birth-death model. It simulates the dynamics of microbial populations and examines how environmental conditions influence spatial patterns. The study concludes that modeling can extract meaningful patterns from experimental data, aiding in the understanding of microbial population dynamics.

1. Exploring microbial patterns formation using a simple IBM
Exploring microbial patterns formation using a
simple IBM
Nabil Mabrouk
www.cemagref.fr
15 decembre, 2009

2. Exploring microbial patterns formation using a simple IBM
Introduction
Introduction
Microscopic observation of microbial systems reveals a
diversity of spatial patterns

3. Exploring microbial patterns formation using a simple IBM
Introduction
Introduction
Microscopic observation of microbial systems reveals a
diversity of spatial patterns

4. Exploring microbial patterns formation using a simple IBM
Introduction
Introduction
Our aim: investigate how these large-scale patterns emerge

5. Exploring microbial patterns formation using a simple IBM
Introduction
Introduction
Our aim: investigate how these large-scale patterns emerge
Our approach: individual-based modeling

6. Exploring microbial patterns formation using a simple IBM
Introduction
Introduction
Our aim: investigate how these large-scale patterns emerge
Our approach: individual-based modeling
Represent the individuals explicitly

7. Exploring microbial patterns formation using a simple IBM
Introduction
Introduction
Our aim: investigate how these large-scale patterns emerge
Our approach: individual-based modeling
Represent the individuals explicitly
Simulate the pattern formation under different conditions

8. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
Model description
Simple is beautiful, and necessary (Deffuant et al., 2003)

9. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles

10. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles
Two processes:

11. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles
Two processes:
death with a probability d

12. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles
Two processes:
death with a probability d

13. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles
Two processes:
death with a probability d
birth with a probability b

14. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles
Two processes:
death with a probability d
birth with a probability b

15. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles
Two processes:
death with a probability d
birth with a probability b
We are interested in the case:
wb << L : local birth

16. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles
Two processes:
death with a probability d
birth with a probability b
We are interested in the case:
wb << L : local birth
b = d = constant

17. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
2D domain with individuals
represented as point particles
Two processes:
death with a probability d
birth with a probability b
We are interested in the case:
wb << L : local birth
b = d = constant
mean-field limit (for large N):
dN
dt = (b − d)N

18. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
Simulation with wb /L = 0.015
Figure: t = 0

19. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
Simulation with wb /L = 0.015
Figure: t = 400

20. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
Simulation with wb /L = 0.1
Figure: t = 400

21. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
Two processes:
death with a probability di ,
i = 1..N
birth with a probability b
We are interested in the case:
wb << L : local birth
birth probability b is
constant

22. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
Two processes:
death with a probability di ,
i = 1..N
birth with a probability b
We are interested in the case:
wb << L : local birth
birth probability b is
constant
death probabilities depend
on the neighborhood (the
pattern)

23. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
Two processes:
death with a probability di ,
i = 1..N
birth with a probability b
We are interested in the case:
wb << L : local birth
birth probability b is
constant
death probabilities depend
on the neighborhood (the
pattern)
||xi −xj ||
di = d1 + d2 j Kd wb

24. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
A simple birth-death model
Overview:
Two processes:
death with a probability di ,
i = 1..N
birth with a probability b
We are interested in the case:
wb << L : local birth
birth probability b is
constant
death probabilities depend
on the neighborhood (the
pattern)
||xi −xj ||
di = d1 + d2 j Kd wb
wb << wd , b > d1 and d2 > 0

25. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
Simulation with wb /L = 0.015 and wd >> wb
Figure: t = 0

26. Exploring microbial patterns formation using a simple IBM
A simple birth-death model
Simulation with wb /L = 0.015 and wd >> wb
Figure: t = 800

27. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
A birth-death model with motility
Overview:
Three processes:
death with a probability di ,
i = 1..N
birth with a probability b
motility with a probability
mi , i = 1..N

28. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
A birth-death model with motility
Overview:
Three processes:
death with a probability di ,
i = 1..N
birth with a probability b
motility with a probability
mi , i = 1..N

29. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
A birth-death model with motility
Overview:
Three processes:
death with a probability di ,
i = 1..N
birth with a probability b
motility with a probability
mi , i = 1..N

30. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
A birth-death model with motility
Overview:
Three processes:
death with a probability di ,
i = 1..N
birth with a probability b
motility with a probability
mi , i = 1..N
We are interested in the case:

31. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
A birth-death model with motility
Overview:
Three processes:
death with a probability di ,
i = 1..N
birth with a probability b
motility with a probability
mi , i = 1..N
We are interested in the case:
motility probabilities depend
on the neighborhood
||xi −xj ||
mi = m1 −m2 j Kv wv

32. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
Parameters
9 parameters:
wb , wd , wm , wv
b, d1 , d2 , m1 and m2
Additional assumptions:
wb (birth) << wd (death)
wm (mobility) >> wb (birth)
wv (”viscosity’) > wd (death)
b >> d1 m1 = 1.0 and d2 , m2 > 0

33. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
Simulation results
Figure: t = 0

34. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
Simulation results
Figure: t = 800

35. Exploring microbial patterns formation using a simple IBM
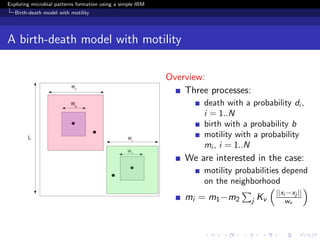
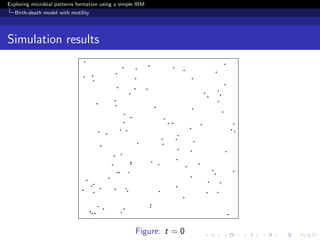
Birth-death model with motility
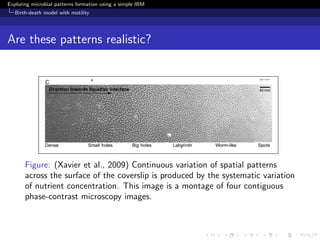
Are these patterns realistic?
Figure: (Xavier et al., 2009) Fluorescent microscopy of yellow
[U+FB02]uorescent protein-labeled biofilm shows cells in spatial patterns
with holes, labyrinths, and wormlike shapes.

36. Exploring microbial patterns formation using a simple IBM
Birth-death model with motility
Are these patterns realistic?
Figure: (Xavier et al., 2009) Continuous variation of spatial patterns
across the surface of the coverslip is produced by the systematic variation
of nutrient concentration. This image is a montage of four contiguous
phase-contrast microscopy images.

37. Exploring microbial patterns formation using a simple IBM
Conclusion
”A change without pattern is beyond Science” (Zeide, 1991)

38. Exploring microbial patterns formation using a simple IBM
Conclusion
”A change without pattern is beyond Science” (Zeide, 1991)
Experimental data contains: meaningful pattern and
misleading noise

39. Exploring microbial patterns formation using a simple IBM
Conclusion
”A change without pattern is beyond Science” (Zeide, 1991)
Experimental data contains: meaningful pattern and
misleading noise
IBM (modeling) can help in extracting patterns and
understanding how they form and impact the population

40. Exploring microbial patterns formation using a simple IBM
Conclusion
”A change without pattern is beyond Science” (Zeide, 1991)
Experimental data contains: meaningful pattern and
misleading noise
IBM (modeling) can help in extracting patterns and
understanding how they form and impact the population
Perspectives ...

41. Exploring microbial patterns formation using a simple IBM
Conclusion
The end!