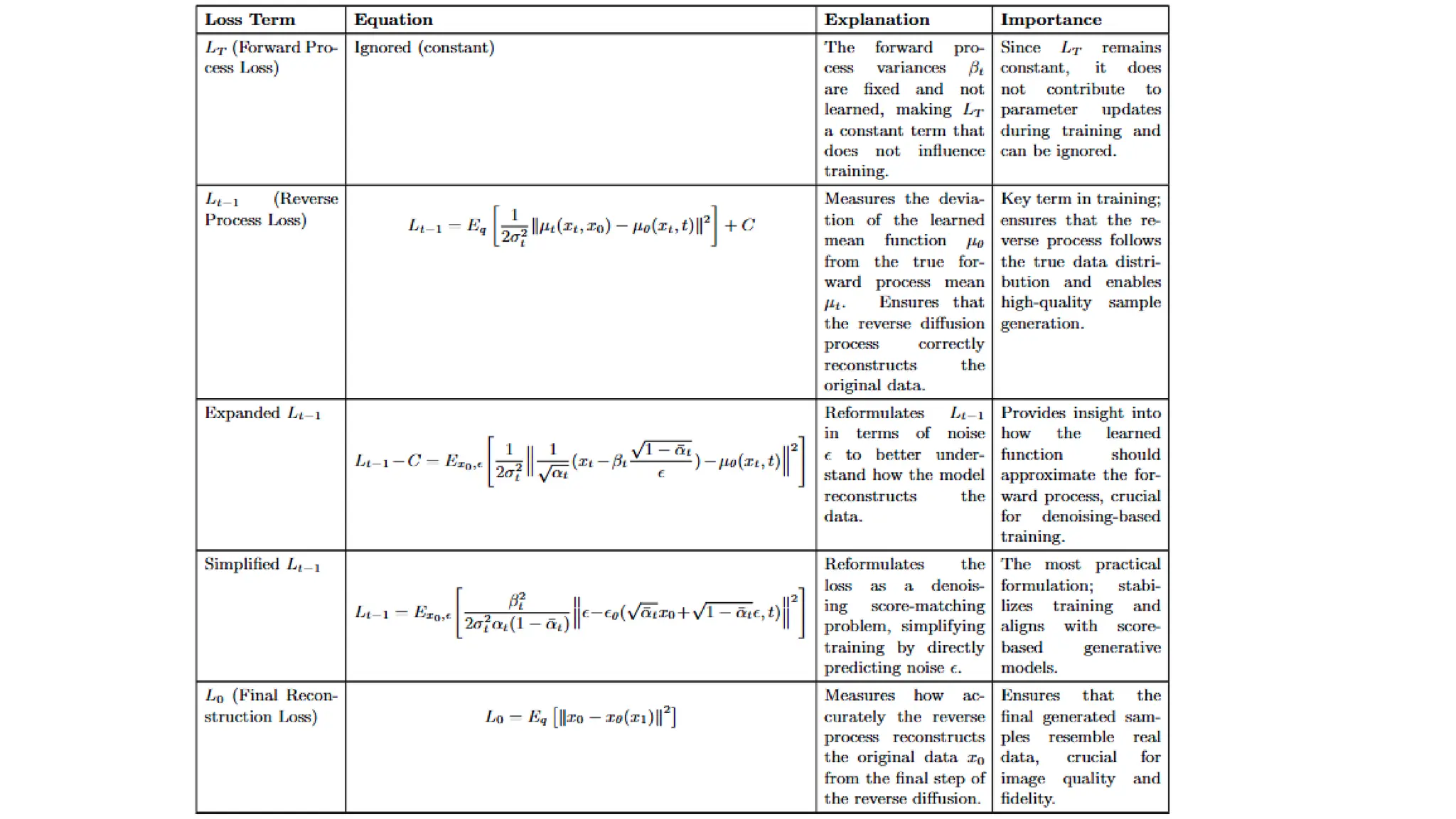
## Explanation of the Math Behind Stable Diffusion (DDPMs) Stable Diffusion is based on **Denoising Diffusion Probabilistic Models (DDPMs)**, which generate images by gradually removing noise. 1. **Forward Process:** Noise is added to an image step by step until it becomes pure noise. 2. **Reverse Process:** A neural network learns to remove this noise, reconstructing a clear image. 3. **Training:** The model is trained to predict and remove noise efficiently. 4. **Image Generation:** Starting from random noise, the model gradually refines the image until it looks realistic.

1. Denoising Diffusion Probabilistic Models

2. Diffusion probabilistic models

4. Background
• Full Latent Variables Model
• We want to model a probability distribution pθ(x0) over data points x0.
• Where XT are latents of the same dimensionality as the data X0 q(X0)
• ) is reverse process defined by Markov Chain with Learned Gaussian
Transitions started at
• Make data pure Gaussian noise with mean 0 and covariance identity
matrix (equal noise in all directions)

12. Equation describes the training objective for diffusion models, which is based on the variational bound
(ELBO: Evidence Lower Bound) on the negative log-likelihood of the data.

27. Image Data Scaling
•Original Image Data: The image pixels are represented as integer values in the range {0, 1, ..., 255}.
•Scaled Data Representation: These pixel values are linearly scaled to [-1,1] using:
Why Scale to [-1,1]? Ensures that the input distribution to the neural network remains consistent.
•Helps in better training stability and convergence.
•Standardizes input for the reverse process.
Standard Normal Prior in Reverse Process
•The reverse process begins with a standard normal prior p(xT), meaning that at the final step of the
forward diffusion, the image data follows a normal distribution:
• The goal of the reverse process (decoder) is to gradually denoise this distribution and reconstruct the original
data.