The document discusses exact differential equations, detailing their history, importance, and applications in various fields such as engineering and computer science. It covers the mathematical foundations laid by notable figures and examines specific case studies demonstrating the use of exact differentials in thermodynamics, fluid dynamics, and machine learning. It also provides problems and solutions related to exact differential equations, illustrating their practical relevance.

1. Exact Differential Equation
𝜹𝑴
𝜹𝒚
=
𝜹 𝑵
𝜹 𝒙
Date: 01-November-2024

2. Role Name ID
Team Leader Indrajith Goswami CSE 031 08143
Member Abdullah Mohammad Galib CSE 031 08007
Member Sharmin Akter Hashi CSE 031 08162
Member Asma Akter Sonia CSE 031 08161
Member Mojibur Rahman CSE 031 08004
Member Jalal Uddin CSE 031 08070
Member Soumya Dey CSE 031 07980
Team Info:
Class Teacher Info:
Name: Dr. Syed Anayet Karim
Designation: Associate Professor
Department of Natural Science

3. What is Exact Differential Equations?
An exact differential indicates a specific type of change in a function that can be expressed in terms of its
variables. It signifies that there is a unique scalar function whose total change can be captured by this
differential. For a differential to be exact, the way the variables interact must satisfy a certain condition,
ensuring that you can derive the function from the differential form. It plays a vital role in various fields,
including mathematics, physics, engineering, and computer science.
𝜹𝑴
𝜹𝒚
=
𝜹 𝑵
𝜹 𝒙

4. History Of Exact Differential Equation
Early Calculus Foundations (17th Century):
Isaac Newton and Gottfried Wilhelm Leibniz independently developed calculus in the late 17th century, establishing the
groundwork for differentiation and integration.
Development of Differential Equations (18th Century):
In the 18th century, Leonhard Euler and Joseph-Louis Lagrange expanded calculus by formalizing differential equations. Euler
explored the solutions to differential equations, laying the foundation for exact differential equations and solutions.
Exact Differential Equations and Integrability Conditions (19th Century):
Augustin-Louis Cauchy and Carl Gustav Jacob Jacobi advanced the theory of differential equations. Cauchy provided rigorous
definitions of functions and continuity, helping differentiate between ordinary and partial differential equations.
Élie Cartan and William Rowan Hamilton formalized criteria for exactness and integrability in differential equations,
establishing conditions under which a differential form could be considered exact.
Thermodynamics and Physics Applications (19th Century):
In thermodynamics, exact differentials became crucial when describing state functions such as energy, entropy, and enthalpy.
Engineers and physicists, such as Rudolf Clausius and James Clerk Maxwell, used exact differentiation to express heat and work
in terms of exact differentials, formalizing thermodynamic laws.
Modern Applications and Computational Advances (20th-21st Century):
As calculus continued to mature, the concept of exact differentials became central in fields such as optimization, fluid dynamics,
electromagnetic theory, and economics. With the rise of computational methods and software, exact differentiation and
differential forms found new applications in numerical analysis, symbolic computation, and control systems.

5. Importance Of Exact Differentiation in Engineering
Exact differentiation, particularly through exact differential equations, plays a crucial role in engineering, as it provides methods to
solve problems involving fields, thermodynamics, fluid mechanics, and electrical engineering. Here’s how it is applied in various
engineering fields:
1. Thermodynamics: Exact differential equations are used to describe state functions like internal energy and enthalpy. For
example, the first law of thermodynamics can be modeled using differential equations.
2. Fluid Dynamics: The Navier-Stokes equations, which describe the motion of fluid substances, are a set of partial differential
equations that can be exact or non-exact depending on the conditions.
 Bernoulli’s Equation: Derived as an exact differential under certain conditions, it relates pressure, velocity, and height in
fluid flow. Engineers use it for pipe flow analysis, pump design, and aerodynamic calculations.
 Potential Flow Theory: For irrotational flows, engineers use potential functions where the differential of the velocity
potential gives the flow velocities, making it easier to analyze complex flow patterns.
3. Electrical Engineering: In electrical engineering, exact differentials appear in circuit analysis, electromagnetic field theory, and
control systems:
 Energy in Capacitors and Inductors: Engineers use exact differential forms to calculate energy stored in capacitors and
inductors, which helps in circuit design and power management.
 Electromagnetic Field Theory: Maxwell’s equations describe electric and magnetic fields as differential forms. Engineers
use these exact forms to design antennas, transformers, and other electromagnetic devices.
4. Structural and Mechanical Engineering: In structural analysis, exact differentials aid in solving equilibrium equations for
static systems:
 Stress and Strain Calculations: Engineers use exact differential equations to relate stress, strain, and displacement in
materials. This relationship is essential for analyzing deformation in beams, bridges, and other structures.
 Potential Energy: The differential of potential energy is exact, which allows engineers to calculate forces, torques, and
stability in mechanical systems.

6. 5. Chemical Engineering: In chemical engineering, exact differentials are used to model reaction rates and equilibrium conditions:
 Reaction Kinetics: Engineers often deal with rates of chemical reactions, where changes in concentration and pressure are
modeled using exact differential equations.
 Mass and Energy Balances: Exact differentials help to compute mass and energy balances in reactors, pipelines, and
separation processes.

7. Why We Use Exact Differentiation in Computer Science Engineering?
Exact differentiation finds several applications in computer science and engineering, especially in fields like optimization, data
science, machine learning, robotics, and even computational physics. Here’s how exact differentiation can be relevant in these
areas:
1. Machine Learning and Optimization: In machine learning, exact differentiation is foundational for optimization techniques,
especially in algorithms where finding a minimum or maximum of a function is required:
 Gradient Descent: To optimize functions (such as cost functions in neural networks), exact derivatives are used to compute
gradients. This is crucial for minimizing errors and improving model accuracy.
 Backpropagation: For training neural networks, exact differentiation allows calculating exact partial derivatives (gradients)
of each layer's parameters, enabling weight adjustments based on exact gradients.
2. Computer Graphics and Image Processing: Exact differentiation is useful for rendering, shading, and image manipulation:
 Shading and Lighting Calculations: In computer graphics, exact differentiation helps in determining gradients for shading
models, allowing for realistic lighting and shadow effects by computing the exact rate of change in pixel intensity.
 Image Filters and Edge Detection: Many image-processing techniques use exact differentiation to detect edges and
gradients, where exact partial derivatives provide precise contour and boundary detection, essential in object recognition
and image segmentation.
3. Robotics and Motion Planning: In robotics, exact differentiation is used in path planning and kinematics:
 Path Planning and Optimization: When planning optimal paths, robots use exact differentiation to calculate the gradient of
potential functions, helping avoid obstacles and efficiently reaching goals.
 Inverse Kinematics: To find joint angles for reaching a point in space, robots use exact partial derivatives, solving complex
kinematic equations in manipulator arms and autonomous systems.
4. Computational Physics and Simulation: In simulation, exact differentiation allows for accurate physical modeling:
 Simulation of Physical Systems: Simulations of fluid dynamics, electromagnetics, or structural mechanics often use exact
differential forms to model real-world phenomena. This enables precise, physics-based simulations in areas such as game
development and scientific computing.

8. 5. Signal Processing: In control theory and signal processing, exact differentiation is crucial for system stability and signal
analysis:
 Signal Analysis: Exact derivatives help in processing signals to extract meaningful features, such as frequency, amplitude, or
phase shifts, by analyzing the exact rate of change in signal waveforms.
6. Data Science and Feature Engineering: Exact differentiation can also contribute to data science by enhancing data
transformation and feature extraction:
 Gradient-Based Feature Engineering: In data preprocessing, exact differentiation can help transform features to better
represent relationships in the data, particularly in nonlinear datasets, which improves model performance.
 Time Series Analysis: Derivatives are used to measure trends and volatility in time series data. Exact differentiation provides
precise trend analysis, especially in domains like finance or weather forecasting, where precise changes are critical.

9. List of Problems
SL. No Question
01 Solve (12x+5y-9)dx + (5x+2y-4)dy = 0.
02 Solve ()dx - (2)dy = 0.
03 Solve dx - ()dy = 0.
04 Solve ()ydx - ()xdy = 0.

10. Problem – 1: Solve (12x+5y-9)dx + (5x+2y-4)dy
= 0.
Solution:
Given,
(12x+5y-9)dx+(5x+2y-4)dy=dy ---- (1)
Differential Equation(1) is in the form of Mdx + Ndy =0, where
M = 12x+5y-9; N = 5x+2y-4
Here we see that
12
Which is required solutions.
Problem – 2: Solve ()dx - (2)dy = 0.
Solution:
Given,
()dx - (2)dy = 0
()dx + (-2)dy = 0
Differential equation(1) is in the form of Mdx+Ndy=0,where
M = -2
Here we see that
Which is required solution.
Problem – 3: Solve dx - ()dy = 0.
Solution:
Given,
dx - ()dy = 0
-----(1)
Here equation(1) is in the form of Mdx+Ndy=0, so M = xy =>
We see that,
Now,
Multiply I.F both sides of (1)=>
=>
Equation(2) is in the form of Mdx+Ndy = 0,
where
In this equation(2) is exect since
Then,

11. Which is required Solution.
Problem – 4: Solve ()ydx - ()xdy = 0.
Solution:
Given,
Equation(1) is in the form of Mdx + Ndy = 0
Here
Now,
So
Multiply I.F both sides of (1) =>
Here equation(2) is exact since
Then,
Which is required Solution.

12. List of Additional Problems
SL. No Question
01 Solve = 0.
Exact Differential
Equation
02 Solve (2x-y+1)dx = (x-2y+1)dy
03 Solve the D.E = -
04 Solution to (3x2
+ 2xy) dx + (x2
+ 4y) dy = 0
05 Solution to (2xy2
+ 3x2
y) dx + (x3
+ 2x2
y) dy = 0
06 Solution to (2x + y) dx + (x + 2y) dy = 0
07 Solution to (y2
- 2xy) dx + (x2
- 2xy) dy = 0
Not Exact but
Homogeneous Differential
Equations
08 Solve = 0.
09 Solve = 0.
10 Solve = 0.
Not Exact and Not
Homogeneous Differential
Equations
11 Solution to (2x + y3
) dx + (x3
- y) dy = 0
12 Solution to (x + y3
) dx + (x3
- y) dy = 0.
13 Solve dx + = 0.

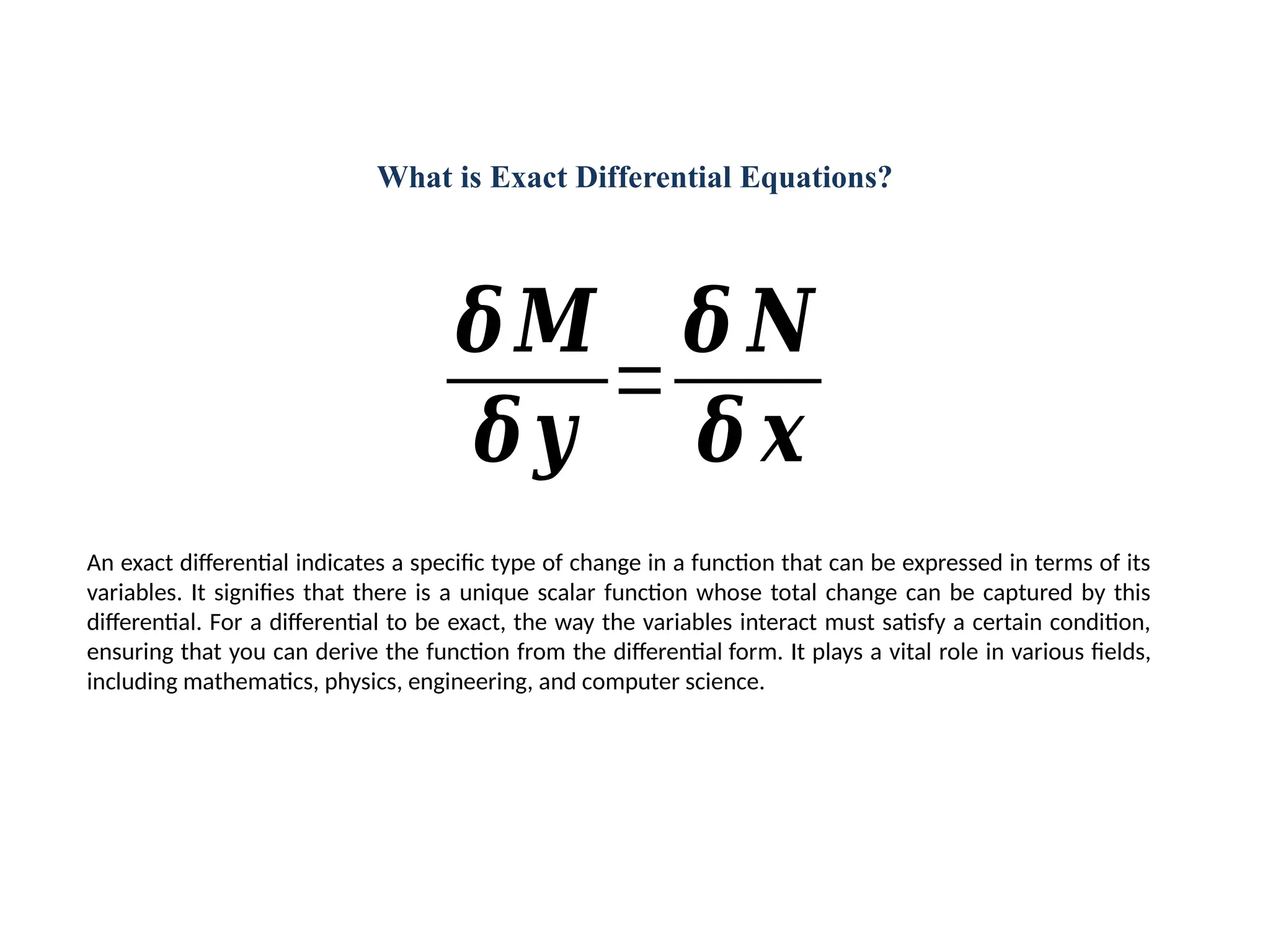
13. Exact Differential Equation:
Problem – 1: Solve = 0.
Solution:
Given,
= 0 ----(1)
Equation(1) is in the form of
Here,
Hence, equation(1) is exact as
Then,
Which is required Solution. Ref: Simmons, G. F. (1991).
Differential equations with applications and historical notes (2nd
ed., p. 126). McGraw-Hill.
Problem-2: Solve (2x-y+1)dx = (x-2y+1)dy
Solution:
Given, D.E. VS
(2x-y+1)dx = (x-2y+1)dy
(2x-y+1)dx – (x-2y+1)dy = 0
Compair it with Mdx+Ndy = 0
 M = 2x-y+1, N= -x+2y-1
= 0-1+0, = -1+0+0
= -1, = -1
Since = = -1
 the given D.E is exact the saln of given DE is given by  mdx +
 (term of N not containing x) dy = C
 (2x-y+1)dx +  (2y-1)dy = C
- xy +1+ -y = C
- xy + x + - y = C
+ - xy + x – y = C
Which is required Solution.Ref: TIKLE'S ACADEMY OF MATHS(Jul
2, 2023), EXACT DIFFERENTIAL EQUATION SOLVED PROBLEM
6[video], https://www.youtube.com/watch?v=K-jYhSc_tpk
Problem-3: Solve the D.E = -
Solution:
Given D.E is
= -
-(2+) dy = dx
dx + (2+)dy=0
Compir it with mdx+ndy=0
M= , N= 2+
= 2xy, = 2xy
Since =
The given D.E is exact
The soln
of given D.E is give by,
Which is the required Solution. Ref: Ref: TIKLE'S ACADEMY OF
MATHS(Jul 2, 2023), EXACT DIFFERENTIAL EQUATION SOLVED
PROBLEM 6[video], https://www.youtube.com/watch?v=K-jYhSc_tpk

14. Problem-4: Solution to (3x2
+ 2xy) dx + (x2
+ 4y) dy = 0
Solution:
Given that
3x2
+ 2xy) dx + (x2
+ 4y) = 0…………….(1)
Differential eqn
(1) is in the form of Mdx+Ndy=0
Where, M = 3x2
+ 2xy and N = x2
+ 4y
Now, = 2x and = 2x
Since so the equation is exact.
Then,
=>+ 2xy)dx + = C
=>3 + 2y + =C
=>3 + 2y+ 4 = C
=> + x2
y +2 y2
= c
Which is the required solution (Ans.) Ref:Simmons, G. F. (1991).
Differential equations with applications and historical notes (2nd
ed., p. 124). McGraw-Hill.
Problem-5:Solution to (2xy2
+ 3x2
y) dx + (x3
+ 2x2
y) dy
= 0
Solution:
Given that
(2xy2
+ 3x2
y) dx + (x3
+ 2x2
y) dy = 0…………….(1)
Differential eqn
(1) is in the form of Mdx+Ndy=0
Where, M = 2xy2
+ 3x2
y and N = x3
+ 2x2
y
Now, = 4xy + 3x2
and = 3x2
+ 4xy.
Since so the equation is exact.
Then,
=>dx = C
=>2y2
+ 3y =C
=>2y2
+ 3y
=> + = C
Þx2
y2
+x3
y = c
Which is the required solution (Ans.)
Ref: Simmons, G. F. (1991). Differential equations with
applications and historical notes (2nd ed., p. 122). McGraw-Hill.
Problem-6: Solution to (2x + y) dx + (x + 2y) dy = 0
Solution :
Given that
(2x + y) dx + (x + 2y) dy = 0…………….(1)
Differential eqn
(1) is in the form of Mdx+Ndy=0
Where, M = 2x + y and N = x + 2y
Now, = 1 and = 1.
Since so the equation is exact.
Then,
=>)dx + = C
=>2 + 2 = C
=>2 + yx +
=> x2
+ xy+ y2
= C
Which is the required solution (Ans.) Ref: Simmons, G. F. (1991).
Differential equations with applications and historical notes (2nd ed., p.
123). McGraw-Hill.

15. Not Exact but Homogeneous Differential
Equations:
Problem-7:Solution to (y2
- 2xy) dx + (x2
- 2xy)
dy = 0
Solution:
dx + ()dy = 0…………..(2)
Equation 1 is the form
Given that
(y2
- 2xy) dx + (x2
- 2xy) dy = 0…………….(1)
Differential eqn
(1) is in the form of Mdx+Ndy=0
Where, M = y2
- 2xy and N = x2
- 2xy
Now, = 2y-2x and = 2x-2y
Since so the equation is not exact but homogeneous
Now,
Mx+Ny = (y2
-2xy)x + (x2
-2xy)y
=xy2
-2x2
y +x2
y-2xy2
The I.F is =
Multiplying both side of equation 1 with I.F we get-
( ) of Mdx + Mdy= 0, Here
M= ; N=
Here =
Then,
=> ( ) dx + = C
=>{( x-2
+ x-1
+ x—2
- x—1
)} dx+ =C
=>(xy2
- xy2
)( + - - ) = c
=> y – x + xlnx - - + - + = C
Which is the required solution. Ref: Boyce, W. E., & DiPrima, R.
C. (2017). Elementary differential equations and boundary value
problems (11th ed., p. 82). Wiley.
Problem – 8: Solve = 0.
Solution:
Given,
= 0
Equation(1) is in the form of
As
Now,
Now dividing both side of equatio(1) with I.F
Equation(2) is in the form of Mdx+Ndy=0. Here,
Now here
Then,

16. Which is the required Solution.
Ref: Boyce, W. E., & DiPrima, R. C. (2017). Elementary
differential equations and boundary value problems (11th ed., p.
83). Wiley.
Problem – 9: Solve = 0.
Solution:
Given,
Equation(1) is in the form of
Here,
As
Now,
Now dividing equation(1) with the I.F
Equation(2) is in the form of Mdx+Ndy = 0.
Here,
As
Then,
Which is the required solution. Ref: Boyce, W. E., & DiPrima, R.
C. (2017). Elementary differential equations and boundary value
problems (11th ed., p. 86). Wiley.

17. Not Exact and Not Homogeneous
Differential Equations:
Problem – 10: Solve = 0.
Solution:
Given,
= 0 --- (1)
Equation(1) is in the form of Mdx+Ndy=0. Here
As
Now,
Now, dividing equation(1) with I.F
-------(2)
Equation(2) is in the form of Mdx+Ndy=0,
Here,
Now,
Then,
Which is the required solution. Ref: Tenenbaum, M., & Pollard, H.
(1985). Ordinary differential equations (p. 71). Dover Publications.
Problem-11: Solution to (2x + y3
) dx + (x3
- y) dy = 0
Solution:
Given that
(2x + y3
) dx + (x3
- y) dy = 0 …………….(1)
Differential eqn
(1) is in the form of Mdx+Ndy=0
Where, M = (2x + y3
) and N = x3
- y
Now, = 3y2
and = 3x2
Since so the equation is not exact and not also homogeneous
Now
Mx-Ny = (2x+y3
)x –(x3
-y)y
=2x2
+xy3
-x3
+y2
The I.F Factor will be
Now dividing eqn
(1) both side with I.F
dx+ dy
= 0…………(2)
Eqn
(2) is in the form of Mdx + Ndy
Where,
M = And N =
Here , so the equation is exact.
Then,
=>)dx + = C
=> = C
=>(2 + xy3
) +(2 + )
=> + + xlnx - - + …… Which is the required solution (Ans.)
Ref: Tenenbaum, M., & Pollard, H. (1985). Ordinary differential
equations (p. 67). Dover Publications.

18. Problem-12: Solution to (x + y3
) dx + (x3
- y) dy = 0.
Solution:
Given that
(x + y3
) dx + (x3
- y) dy = 0 …………….(1)
Differential eqn
(1) is in the form of Mdx+Ndy=0
Where, M = (x + y3
) and N = x3
- y
Now, = 3y2
and = 3x2
Since so the equation is not exact and not also homogeneous
Now
Mx-Ny = (x+y3
)x –(x3
-y)y
=x2
+xy3
-x3
+y2
The I.F Factor will be
Now dividing eqn
(1) both side with I.F
dx+ dy
= 0…………(2)
Eqn
(2) is in the form of Mdx + Ndy
Where,
M = And N =
Here , so the equation is exact.
Then,
=>)dx + = C
=> = C
=>( + xy3
) +( + )
=> + + xlnx - - + …… Which is the required solution (Ans.) Ref:
Tenenbaum, M., & Pollard, H. (1985). Ordinary differential equations (p.
68). Dover Publications.
Problem-13: Solve dx + = 0.
Solution:
Given D.E
dx + = 0
Compare it with mdx+ndy=0
M= , N= =0
M= , N=
M= + N= -
M= 2x+ , N= -
,
Here,
The given D.E is Exact
The soln
is given by,
Which is the required Solution.
Ref: TIKLE'S ACADEMY OF MATHS(Jul 2, 2023), EXACT
DIFFERENTIAL EQUATION SOLVED PROBLEM 6[video],
https://www.youtube.com/watch?v=K-jYhSc_tpk

19. Conclusion
In summary, exact differentiation has grown from a foundational idea in calculus into a vital tool
across science and engineering. Starting with Newton and Leibniz, and expanded by Euler and
Cauchy, it has become essential for solving complex systems and understanding physical
processes accurately.
In engineering, exact differentiation helps in modeling thermodynamics, fluid flow, and
electromagnetics. In computing, it enables optimizations in machine learning, realistic graphics,
and precise simulations. These uses show how it solves practical challenges and remains relevant
today.
As computational methods and AI continue to grow, exact differentiation will keep enabling new
solutions and innovations. Its journey from theory to widespread application shows both its
historical importance and its ongoing role in advancing technology and science. Thank you for
exploring exact differentiation with us.

20. Thank you