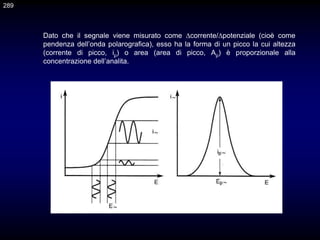
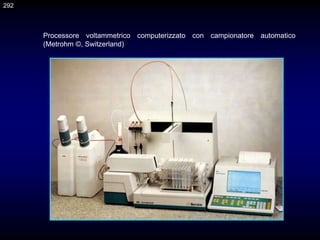
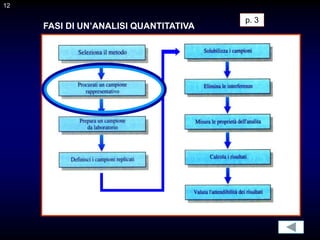
Il documento fornisce un'introduzione alla chimica analitica, evidenziando i concetti fondamentali e le tecniche utilizzate. Include dettagli su metodi di analisi, esercitazioni pratiche e organizzazione del corso, con un focus su sicurezza e valutazione. Viene anche discussa la natura interdisciplinare della chimica analitica e le sue applicazioni in vari ambiti.















![17
FUNZIONI p
In notazione scientifica, l’operatore p indica il logaritmo negativo
del valore della grandezza in oggetto.
Keq = 5.10-16 pKeq = - log (Keq) = 15,30
[H+] = 2.10-4 M pH = - log [H+] = 3,70
[Cl-] = 7.10-11 M pCl = 10,15
S (solubilità) = 2,5.10-8 mg/kg pS = 7,60
Nel caso si voglia riportare in grafico la [H+] delle soluzioni
acquose conviene usare una scala lineare o logaritmica?
p. 21
17](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-17-320.jpg)










![29
EQUILIBRIO CHIMICO
Per una reazione generica
aA + bB = cC + dD
Possono essere scritte una costante TERMODINAMICA ed una
COSTANTE stechiometrica:
p. 34
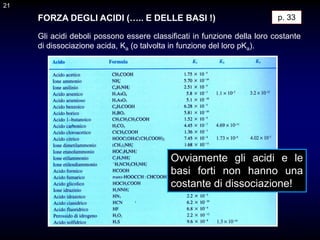
29
b
B
a
A
d
D
c
C
eq
a
a
a
a
K T
L’attività di composti ed
elementi puri è unitaria e
non compare nell’equazione
della costante di equilibrio.
b
a
d
c
eq
B
A
D
C
K st
La concentrazione di composti ed
elementi puri (o praticamente puri,
come nel caso dell’acqua quando è
il solvente di soluzioni diluite), è
praticamente costante, e non
compare nell’equazione della
costante di equilibrio.
[H2O] (solvente sol. dil.) = costante =
1000/18 = 55,5 M](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-29-320.jpg)

![31
2H2O = H3O+ + OH-
Kw25°C = K.[H2O]2 =[H3O+ ].[OH-] = 1.008.10-14
Costante di dissociazione stechiometrica di un acido debole, HA
HA + H2O = H3O+ + A-
Ka
25°C = Ka.[H2O] = [H3O+ ].[A-]/[HA]
Costante di dissociazione stechiometrica di una base debole, A-
A- + H2O = OH- + HA
Kb
25°C = Kb.[H2O] = [OH- ].[HA]/ [A-]
Prodotto di solubilità termodinamico del solfuro di argento
Ag2S = 2Ag+ + S2- Ks
25°C = (aAg+) 2.(aS2-)
Prodotto ionico stechiometrico dell’acqua
31
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-31-320.jpg)

![33
Per trascurare una concentrazione rispetto ad un'altra è necessario
definire quantitativamente il livello di concentrazione al di sotto del quale
l'approssimazione è accettabile.
Il criterio d’approssimazione è funzione dell'errore di calcolo
massimo accettabile, indicato talvolta con EMA.
Potremo così decidere, per esempio, che la specie A è trascurabile
rispetto alla specie B quando la sua concentrazione è minore del 10% di
quella della specie B (EMA = 10%).
33
]
B
[
100
%
EMA
]
A
[
se
]
B
[
]
A
[
Qual è il valore normale dell’EMA?
In mancanza di indicazioni diverse, l’EMA è normalmente uguale al 5%.
È pertanto inutile pretendere di svolgere i calcoli con maggiore precisione.
p. 127](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-33-320.jpg)
![34
pH di acidi e basi forti
Si può dimostrare che la concentrazione idrogenionica di una soluzione
contenente la concentrazione Ca di un acido forte è calcolabile per mezzo
dell’equazione:
Analogamente, per una soluzione contenente la concentrazione Cb di un
base forte, si ha:
]
H
[
K
C
]
H
[ W
a
]
OH
[
K
C
]
OH
[ W
b
Il pH di una soluzione contenente un acido forte è uguale a -log(Ca) (e
quello di di una soluzione contenente una base forte è uguale a -log(Cb))
solo se il contributo dell’acqua (espresso dal termine Kw/[H+]) è
trascurabile.
34](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-34-320.jpg)
![35
Calcolare il pH di una soluzione 3,0.10-4 M (Cb) di NaOH.
Kw = [H+ ].[OH-] = 1.00.10-14
[H+ ] + [Na+] = [H+ ] + Cb = [OH-] [OH- ] = Cb = 3,0.10-4 M
pH = 14 –[-log (3,0.10-4 )]
pH = 10,48
35
Esempi
Calcolare il pH di una soluzione 1,0.10-8 M di HNO3.
pH = -log(Ca) = -log(1,0.10-8) = 8,0
Ma allora la soluzione è basica ???
[H+] = Ca + Kw/ [H+] [H+]2 – Ca. [H+] – Kw = 0
La risoluzione dell’equazione di 2° grado porta a [H+] = 1,051.10-7
M e quindi a pH = 6,98](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-35-320.jpg)
![36
SISTEMI ACIDO-BASE CONIUGATI
Le costanti di dissociazione dell’acido e della base di una coppia
coniugata non sono indipendenti:
]
A
[
]
OH
[
]
HA
[
Kb
]
HA
[
]
A
[
]
H
[
Ka
14
w
b
a 10
0
,
1
K
]
OH
[
]
H
[
]
A
[
]
OH
[
]
HA
[
]
HA
[
]
A
[
]
H
[
K
K
36
p. 43](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-36-320.jpg)
![37
La costante di dissociazione di un acido debole
può essere convenientemente riscritta così ]
HA
[
]
A
[
]
H
[
Ka
37
Questo permette di valutare l’entità della dissociazione dell’acido noto il pH.
IPOTESI: L’acido sia considerabile dissociato se HA è solo il 5% di A-, ovvero
EMA = 5%
Allora:
3
.
1
pK
)
5
100
log(
pK
pH
e
100
]
H
[
K
a
a
a
Analogamente, l’acido sia considerabile associato se A- è solo il 5% di HA
EMA = 5%
Allora
3
.
1
pK
)
100
5
log(
pK
pH
e
10
]
H
[
K
a
a
2
a
](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-37-320.jpg)
![38
Per quanto detto, accettando un EMA = 5%, per un acido debole di
costante Ka si può scrivere quanto segue:
38
dissociato
acido
pH
]
3
.
1
pK
[
dissociato
te
parzialmen
acido
]
3
.
1
pK
[
pH
]
3
.
1
pK
[
to
indissocia
acido
]
3
.
1
pK
[
pH
a
a
a
a
Analogamente, accettando un EMA = 10%, per un acido debole di
costante Ka si può scrivere quanto segue:
dissociato
acido
pH
]
0
.
1
pK
[
dissociato
te
parzialmen
acido
]
0
.
1
pK
[
pH
]
0
.
1
pK
[
to
indissocia
acido
]
0
.
1
pK
[
pH
a
a
a
a
E se l’errore ammesso è solo l’ 1% ?](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-38-320.jpg)
![39
CALCOLO DEL PH DI SOLUZIONI CONTENENTI ACIDI
DEBOLI
Si può dimostrare che la concentrazione idrogenionica in una soluzione
contenente un acido debole è calcolabile mediante l’equazione esatta:
]
H
[
K
]
H
[
K
C
K
]
H
[ W
a
a
a
39
Molto spesso la concentrazione degli ioni idrogeno provenienti dalla
dissociazione dell’acqua è trascurabile, e il calcolo del pH di una
soluzione contenente un acido debole può essere eseguito usando
l’equazione
]
H
[
K
C
K
]
H
[
a
a
a
2
Ca
K
4
K
K
]
H
[ a
2
a
a
p. 45](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-39-320.jpg)
![40
40
L’equazione di 2° grado è più sicura di quella normalmente usata
p. 46
a
a C
K
]
H
[
a
a
a
a
a
a
a
C
.
K
]
H
[
]
H
[
C
K
]
H
[
K
C
K
]
H
[
Infatti, essa è accettabile solo se il contributo dell’acqua è trascurabile e
l’acido è considerabile completamente associato.
Qualora EMA = 5%, Ka è molto minore di [H+] se pH < (pKa -1,3) e
quindi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-40-320.jpg)
![41
Calcolare il pH di una soluzione contenente ac. acetico
0,02 M (Ka = 1,75.10-5) (EMA: 5%).
Calcolare il pH di una soluzione contenente ac. acetico
3.10-5 M (EMA: 5%).
[H+] = (KaCa)0,5 = 5,92.10-4 M; pH = 3,23
pH = 3,23
M
10
.
83
,
5
2
Ca
K
4
K
K
]
H
[ 4
a
2
a
a
[H+] = (KaCa)0,5 = 2,29.10-5 M ; pH = 4,64
pH = 4,80
M
10
.
58
,
1
2
Ca
K
4
K
K
]
H
[ 5
a
2
a
a
41
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-41-320.jpg)
![42
42
Nel caso di un acido debole di concentrazione Cd e di uno forte di
concentrazione Cf, e ammesso che la concentrazione di ioni idrossido
sia trascurabile, per calcolare il pH si può usare l’equazione
Questo è il caso di una soluzione contenente, per es. acido nitrico e
acido butirrico. Spesso l’acido forte impedisce la dissociazione
dell’acido debole. Nell’equazione viene trascurata la concentrazione
degli ioni idrossido.
f
a
d
a
f
d C
]
H
[
K
C
K
]
A
[
]
A
[
]
H
[
CALCOLO DEL PH DI SOLUZIONI CONTENENTI
CONTEMPORANEAMENTE ACIDI DEBOLI E ACIDI FORTI](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-42-320.jpg)
![43
Calcolare il pH di una soluzione contenente ac. acetico
0,02 M (Ka = 1,75.10-5) e HNO3 1,5.10-3 M.
L’ac. nitrico è completamente dissociato. Gli ioni idrogeno da esso
generati potrebbero far retrocedere la dissociazione dell’ac. acetico
(Le Chatelier).
Dall’esercizio precedente sappiamo che se quest’ultimo fosse
presente da solo produrrebbe [H+] = 5,83.10-4 M (grado di
dissociazione 2,92%).
Il pH calcolabile sulla base del solo ac. forte è –log(1,5.10-3) = 2.82
Come rispondere alla domanda?
Dalla costante di dissociazione dell’acido debole otteniamo:
0117
,
0
10
.
5
,
1
10
.
75
,
1
]
H
[
K
]
HA
[
]
A
[
3
5
a
Allora che dobbiamo fare? Qual è il pH della soluzione?
43
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-43-320.jpg)
![44
Calcolare il pH di una soluzione Ca M di ac. solforico.
La prima dissociazione dell’ac. solforico è completa. Lo ione HSO4
-
invece è un acido debole:
H2SO4 + H2O H3O+ + HSO4
-
HSO4
- + H2O = H3O+ + SO4
2-
Quindi una soluzione di ac. Solforico equivale ad una soluzione
contenente un acido forte ed uno debole di uguale concentrazione.
Pertanto il calcolo del pH richiede l’uso della seguente equazione:
44
a
a
a
a
C
]
H
[
K
C
K
]
H
[
2
C
K
8
)
K
C
(
)
K
C
(
]
H
[ a
a
2
a
a
a
a
Quindi la
concentrazione di ioni
idrogeno è data da:
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-44-320.jpg)
![45
La frazione dissociata di acido debole è quindi
Le due equazioni sono utili per valutare quale/i specie prevalgono in
soluzione.
(il pedice indica il numero di protoni presenti nella specie di cui è
calcolata la frazione) e dato che la somma delle frazioni di acido
dissociato e indissociato deve essere uguale a 1,0, la frazione di
acido indissociato è
45
]
H
[
K
K
C
]
A
[
a
a
a
0
]
H
[
K
]
H
[
C
]
HA
[
a
a
1
FRAZIONE DISSOCIATA E FRAZIONE ASSOCIATA DI UN ACIDO
DEBOLE](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-45-320.jpg)
![46
Come si può calcolare il pH di soluzioni contenenti sali di acidi o
di basi deboli monoprotici con basi e rispettivamente acidi forti
(cloruro ammonico, NH4Cl, cianuro sodico,NaCN, …) ?
46
Le soluzioni dei sali di acido debole con base forte sono in effetti
soluzioni contenenti una base debole:
NaCN Na+ + CN-
CN- + H2O = HCN + OH-
Quindi in questi casi si usano equazioni simili a quelle sviluppate
per gli acidi deboli. Per esempio:
]
H
[
K
C
K
]
H
[
a
a
a
]
OH
[
K
C
K
]
OH
[
b
b
b
E nel caso di sali di basi deboli con acidi forti?](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-46-320.jpg)
![47
Per i sali acidi dell’ac. debole H3A valgono le equazioni:
NaH2A Na2HA
che talvolta possono essere approssimate a
s
1
a
s
2
a
1
a
w
1
a
C
K
C
K
K
K
K
]
H
[
s
2
a
s
3
a
2
a
w
2
a
C
K
C
K
K
K
K
]
H
[
2
a
1
a K
K
]
H
[
3
a
2
a K
K
]
H
[
47
CALCOLO DEL PH DI SOLUZIONI CONTENENTI SALI ACIDI
(OVVERO DI SALI DEL TIPO MxHyA)
Per i sali acidi tipo NaHA vale l’equazione
e quella approssimata
s
1
a
s
2
a
1
a
w
1
a
C
K
C
K
K
K
K
]
H
[
2
a
1
a K
K
]
H
[
](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-47-320.jpg)
![48
Quando sono applicabili le equazioni semplificate? Ne esistono altre?
Come ci si deve regolare? Sono possibili diversi casi:
oppure …
s
1
a
s
2
a
1
a
C
K
C
K
K
]
H
[
s
1
a
s
2
a
1
a
w
1
a
C
K
C
K
K
K
K
]
H
[
s
2
a
w C
K
K
1
a
s
2
a
w
K
C
K
K
]
H
[
s
1
a
s
2
a
1
a
w
1
a
C
K
C
K
K
K
K
]
H
[
1
a
s K
C
e così via …
Conviene sempre valutare le possibili approssimazioni ed utilizzare
l’equazione più semplice da esse derivante.
48](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-48-320.jpg)









































![95
Come anticipato nel Cap. 3, il prodotto di solubilità è funzione della
solubilità.
Nell’ipotesi che si sciolgano S moli del sale in oggetto:
AgCl = Ag+ + Cl- Ks
25°C = [Ag+ ].[Cl-] = S2
S S + S
Ag2SO4 = 2Ag+ + SO4
2- Ks
25°C = [Ag+ ]2.[SO4
2-] = (2S)2.S
S 2S + S
Fe3(PO4)2 = 3Fe2+ + 2PO4
3- Ks
25°C = [Fe2+ ]3.[PO4
3-]2 =
S 3S + 2S = (3S)3. (2S)2
Una soluzione in equilibrio termodinamico con un eccesso di analita
indissolto (corpo di fondo) si dice satura. La concentrazione di analita
presente in una soluzione satura, ad una certa temperatura, è la
solubilità, S.
95
p. 40](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-95-320.jpg)


![98
98
Calcolare la solubilità dello ioduro di Bario in acqua.
S moli/Lsolido S moli/Lsoluz S moli/L Ba2+ + 2S moli/L l-
(BaI2)solido (Bal2)soluzione Ba2+ + 2 l-
Calcolare la solubilità dell’idrossido di Fe(II) a pH = 9.0
Dato che Ks = [Fe2+ ] [OH-]2 e che [OH-] = 10-5 M
S = Ks/(10-5)2 S = (4,1.10-15)/ 10-10 = 4,1.10-5 M
Questa non è la solubilità dell’idrossido in acqua, ma quella
dell’idrossido in una soluzione portata a pH = 9,0 !
Esempi
Dato che Ks = [Ba2+ ][l-]2 allora Ks = S.(2S)2 3 S
4
K
S ](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-98-320.jpg)






![106
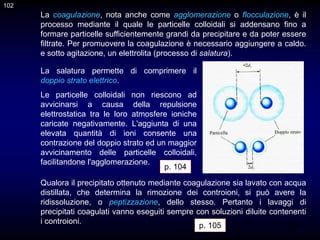
Come si può semplificare il calcolo?
a
s
2
K
]
H
[
1
K
S
a
s
2
K
H
K
S
s
2
K
S
Il pH è << di pKa ?
a
s
2
K
]
H
[
1
K
S
Il pH è >> di pKa ?
a
s
2
K
]
H
[
1
K
S
106
Si può dimostrare che l’equazione utile è la seguente:](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-106-320.jpg)
![107
107
Calcolare la solubilità del cianuro di argento a pH = 4,0 (EMA: 5%).
Il Ks del sale è 2,2.10-16. La Ka è 6,2.10-10.
S 2.2 10
16
S 1.483 10
8
S corr
2.2 10
16
10
4
6.2 10
10
S corr 5.957 10
6
S corr
S
401.61
Il Ks del sale è 2,2.10-16. La Ka è 6,2.10-10.
In assenza di effetto-pH la solubilità è quella in acqua, cioè S. Ma se
pH << pKa, allora [H+] >> Ka (l’acido è completamente associato) e
allora la solubilità diventa uguale a Scorr
Errato!
Corretto!
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-107-320.jpg)





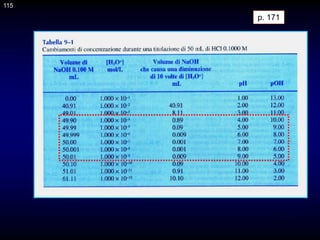

![117
CAPITOLO 10 - TEORIA DELLE TITOLAZIONI DI
NEUTRALIZZAZIONE
p. 174 -175
Gli indicatori normalmente usati per l'identificazione del punto di arresto di
una titolazione acido-base sono coppie coniugate acido/base
caratterizzate dal fatto che l'acido e la base coniugati (indicati con HIn e
In-) hanno diverso colore.
Nel caso di un indicatore generico HIn, avente costante di dissociazione
acida Kin, si ammette di riuscire a distinguere il colore dell'acido o della
base coniugata quando il rapporto [In-]/[HIn] è uguale a 0,1 o 10,
rispettivamente. L'intervallo di pH corrispondente a questa variazione del
rapporto [In-]/[HIn] è ovviamente uguale
117
]
HIn
[
]
In
[
]
H
[
KIn
pH = pKIn ± 1
Quindi, normalmente si assume che il viraggio di un indicatore avvenga in
circa due unità di pH.](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-117-320.jpg)




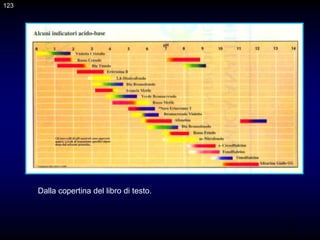
![124
Calcolo del pH di soluzioni tampone
Sistema di 5 equazioni in 5 incognite:
Kw = [H3O+ ].[OH-] = 1.00.10-14
Ka [HA] = [H3O+ ].[A-]
CA = [Na+]
CHA + CA = [HA] + [A-]
[Na+] + [H3O+ ] = [OH-] + [A-]
]
O
H
[
]
OH
[
C
]
O
H
[
]
OH
[
C
K
]
O
H
[
3
A
3
HA
a
3
]
O
H
[
C
]
O
H
[
C
K
]
O
H
[
3
A
3
HA
a
3
……….
Come al solito esistono
un’equazione esatta e più
equazioni approssimate.
p. 182
A
HA
a
3
C
C
K
]
O
H
[
Equazione di Henderson-Hasselbalch
124](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-124-320.jpg)
![125
Calcolare il pH di una soluzione contenente ac. piruvico
0,02 M e piruvato di potassio 0,001 M.
C HA 0.02 C A 0.001 Ka 0.0032
H Ka
C HA
C A
H 0.064
Dato che H Ka
C HA H
C A H
H
Ka C A Ka C A
2
4 Ka
C HA
2
H 6.171 10
3
Come prevedibile, in
questo caso l’uso
dell’equazione di
Henderson-Hasselbalch
porta ad un risultato
sbagliato.
Di quanto è sbagliato?
Perché è sbagliato?
125
Perché spesso si può
ipotizzare che
CA>>[H+] e CA>>[OH-]
e
CHA>>[H+] e CHA>>[OH-] ?
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-125-320.jpg)
![126
Spiegare intuitivamente perché la capacità tampone è
massima a pH = pKa
+2H+ -2H+
CHA/CA
52/48 = 1,08 50/50 = 1,00 48/52 = 0,92
97/3 = 32,2 95/5 = 19,0 93/7 = 13.3
99/1 = 99,0 97/3 = 32,3 95/5 = 19,0
Come si deve scegliere un sistema tampone dato il pH al
quale si deve tamponare?
Il pH dipende dal rapporto [HA]/[A-]
126
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-126-320.jpg)





![132
Vediamo come si può tracciare la curva di titolazione mediante calcoli
approssimati.
Il caso più semplice è quello delle titolazioni simmetriche di precipitazione,
quelle in cui il rapporto stechiometrico di reazione è 1:1. Consideriamo la
titolazione di 40 mL di una soluzione di bromuri circa 0,1 M con una
soluzione di ioni argento 0,1000 M.
Br- + Ag+ = AgBr
Le equazioni utili sono le seguenti.
Prima del p.e.:
Al p.e.:
Dopo del p.e.:
V
40
)
V
40
(
1
,
0
]
Br
[
s
K
]
Ag
[
]
Br
[
V
40
)
40
V
(
1
,
0
]
Ag
[
V
40
)
40
V
(
1
,
0
K
]
Br
[ s
La curva di titolazione si costruisce riportando il pAg, o il pBr, sull'asse
delle ordinate ed il volume di titolazione su quello delle ascisse.
p. 239
132](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-132-320.jpg)
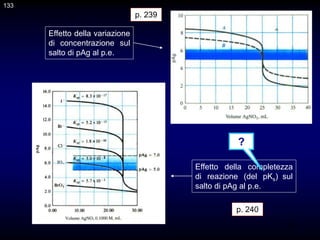



![137
CAPITOLO 14 - TITOLAZIONI CON FORMAZIONE
DI COMPLESSI
Nelle reazioni di complessazione, specie elettron-donatrici, i leganti
(basi di Lewis), formano legami covalenti dativi con uno ione positivo
(acido di Lewis). Se lo ione coordinante è idratato, la reazione consiste
nello spostamento del legante acqua da parte di un legante più basico
(base di Lewis più forte)
[M(H2O)n]z+ + nL = [MLn]z+ + nH2O
Il numero massimo di legami covalenti dativi formati da un catione (n
nella reazione qui sopra) viene chiamato numero di coordinazione.
p. 248
Dato che i leganti possono essere molecole neutre (NH3, H2O, ecc.) o
ioni negativi (CN-, Cl-, SO4
2-, ecc.) le specie complesse in soluzione
possono essere neutre (CuCl, Fe(CN)3, ecc.) o possedere una carica
positiva (Ag(NH3)2+, FeCN2+, ecc.) o negativa (Ag(NH3)Br2
-, Fe(CN)6
4-,
Cd(OOCH)3
-, ecc.).
137](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-137-320.jpg)
![138
Esempi di ioni complessi in soluzione p. 135
138
]
)
CH
OOC
(
Ni
[
]
CuCl
[
]
CuCl
[
]
)
CN
(
Fe
[
]
)
CN
(
Fe
[
]
)
NH
(
Ag
[
2
3
2
3
6
4
2
3
Esempi di costanti di formazione di ioni complessi
2
3
2
3
2
1
tot
2
3
3
3
3
2
3
2
2
2
3
3
3
3
3
1
1
3
3
]
NH
[
]
Ag
[
]
)
NH
(
Ag
[
K
K
K
)
NH
(
Ag
NH
2
Ag
]
NH
[
]
)
NH
(
Ag
[
]
)
NH
(
Ag
[
K
)
NH
(
Ag
NH
)
NH
(
Ag
]
NH
[
]
Ag
[
]
)
NH
(
Ag
[
K
)
NH
(
Ag
NH
Ag
Normalmente, le costanti di formazione sono maggiori di 1,0.
La costante K1 qui sopra è uguale a 2041.7 (log(K1) = 3,31).](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-138-320.jpg)

![140
140
Calcolare il rapporto tra concentrazione dello ione argento libero
e concentrazione dello ione [Ag(NH3)2]+ in una soluzione di nitrato
di argento nella quale è presente NH3 libera 0,04 M.
L’argento forma 2 specie complesse, [Ag(NH3)]+ e [Ag(NH3)2]+.
2
3
2
1
2
3
2
3
2
3
2
1
]
NH
[
K
K
1
]
)
NH
(
Ag
[
]
Ag
[
]
NH
][
Ag
[
]
)
NH
(
Ag
[
K
K
L’argento è presente prevalentemente come ione [Ag(NH3)2]+
.
K 1 10
3.31
K 2 10
3.91
K 1 K 2
1.66 10
7
C NH3 0.04 R
1
K 1 K 2
C NH3
2
R 3.766 10
5
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-140-320.jpg)





![146
Costanti condizionali
La reazione di complessazione teorica tra uno ione M e l’EDTA* può
essere così scritta
M + Y = MY
ma, in funzione del pH, l’EDTA può essere presente in una o più delle sue
forme protonate. In altre parole vale il bilancio di massa
CY = [H4Y] + [H3Y] + [H2Y] + [HY ]+ [Y]
Quindi, data la costante stechiometrica
e definendo 4 come segue
* Per semplicità, le cariche delle specie coinvolte in equilibri di complessazione possono
essere tralasciate.
]
Y
[
]
M
[
]
MY
[
KMY
Y
4
C
]
Y
[
Y
MY
4
'
MY
C
]
M
[
]
MY
[
K
K
otteniamo
p. 254
146
Si noti che il testo usa come
pedice delle frazioni il numero
delle cariche. K’MY è una
costante condizionale!](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-146-320.jpg)

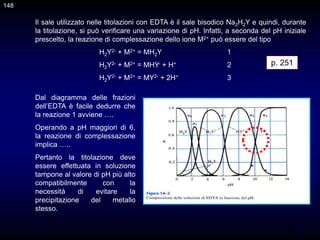

























![ V° è indipendente dal numero di moli di reagenti e di prodotti che
compaiono nella semireazione bilanciata. Perciò, il potenziale
elettrodico standard per la semireazione.
Fe3+ + e- = Fe2+ V° = +0.771
non cambia se si sceglie di scrivere la reazione nel seguente modo
5Fe3+ + 5e- = 5Fe2+ V° = +0.771
p. 286
5
2
5
3
2
3
]
Fe
[
]
Fe
[
log
5
0591
,
0
771
,
0
]
Fe
[
]
Fe
[
log
1
0591
,
0
771
,
0
V
Un valore positivo di V° indica che quando la semicella alla quale si
riferisce è collegata allo SHE, la reazione spontanea è quella di
riduzione.
V° dipende dalla temperatura! Il potenziale standard indipendente
dalla temperatura è solo quello dell’elettrodo standard a idrogeno.
177](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-177-320.jpg)


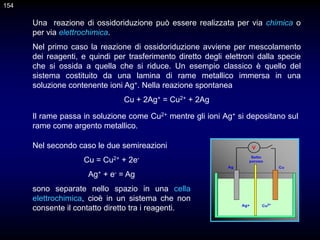
![ Calcolare la costante di equilibrio (25°C) della reazione
Cu(s) + 2Ag+ = Cu2+ +2Ag(s)
La costante in oggetto è: 2
2
eq
]
Ag
[
]
Cu
[
K
Per quanto dimostrato in precedenza: 61
,
15
0591
,
0
)
V
V
(
2
K
log
Cu
Ag
eq
Quindi Keq = 4,1.1015.
Con uguale procedimento si può calcolare la costante di equilibrio (25°C) della
reazione
5Fe2+ + MnO4
- +5e- = 5Fe3+ +Mn2+ +4H2O
Per quanto dimostrato in precedenza:
52
,
62
0591
,
0
)
771
,
0
51
,
1
(
5
0591
,
0
)
V
V
(
5
K
log Fe
Mn
eq
Quindi Keq = 3,3.1062.
180
Esempi](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-180-320.jpg)





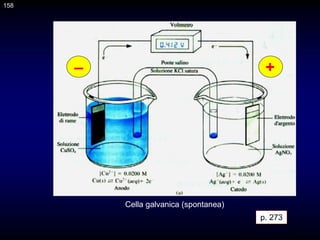
![Il rilevamento del punto di arresto della titolazione può essere fatto per
via strumentale, monitorando il potenziale al variare del volume di
titolante aggiunto (cioè mediante titolazioni potenziometriche - Cap. 18),
oppure utilizzando indicatori di ossidoriduzione.
Questi ultimi sono costituiti da sostanze caratterizzate da un diverso
colore delle forme ossidata e ridotta e rispondono quindi alle variazioni di
potenziale elettrodico di un sistema (indicatori generali di
ossidoriduzione) o da sostanze nelle quali la variazione di colore è
determinata da reazioni con uno dei partecipanti alla titolazione
(indicatori specifici di ossidoriduzione). I primi sono più versatili e hanno
maggiori applicazioni mentre i secondi vengono utilizzati in casi
particolari.
]
In
[
]
In
[
ln
nF
RT
V
V
rid
oss
Nel caso di un indicatore generale, In, possiamo scrivere la reazione
Inoss + ne- = Inrid
e, se la reazione è reversibile, possiamo scrivere
186
p. 313](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-186-320.jpg)
![Allora, se ammettiamo di riuscire ad osservare la variazione di colore
dell'indicatore quando il rapporto [Inoss]/[Inrid] cambia da 10 (soluzione
caratterizzata dal colore della forma ossidata) a 0,1 (soluzione
caratterizzata dal colore della forma ridotta), o viceversa, possiamo
concludere che l'intervallo di potenziale al viraggio è
cioè l'intervallo di viraggio è largo 0,118/n V, ed è centrato intorno a V°In,
(in realtà intorno al potenziale reale di viraggio, V°'In, cioè intorno al
potenziale formale dell'indicatore). Dato che per molti indicatori n = 2
l'intervallo di viraggio è circa di 60 mV.
n
0591
,
0
V
V In
Un indicatore specifico molto utile
nell’analisi alimentare è l'amido
che forma un complesso blu intenso con lo
ione I3
-
(cioè con lo iodio in presenza di ioduro) e
può essere usato come indicatore in tutte le
reazioni che impiegano lo iodio come
ossidante o lo ioduro come riducente.
187
p. 314](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-187-320.jpg)


![CLASSIFICAZIONE STRUTURALE DEGLI ELETTRODI
Gli elettrodi sono classificabili come elettrodi di Ia e IIa specie, elettrodi di
ossidoriduzione ed elettrodi a membrana.
Gli elettrodi di Ia specie
M/Mn+
sono costituiti da un metallo immerso in una soluzione di suoi ioni. La corrispondente
reazione elettrodica è la seguente
Mn+ + ne- = M
L'elettrodo di zinco e quello di rame usati nella pila Daniell sono di Ia specie.
L'equazione di Nernst per questi elettrodi è del tipo
)
a
log(
n
0591
,
0
V
V n
M
]
M
log[
n
0591
,
0
V
V n
Il potenziale degli elettrodi di Ia specie dipende quindi dall'attività dei cationi del
metallo elettrodico. Un elettrodo di Ia specie ad Al/Al3+ può essere utilizzato, per
esempio, per misurare la concentrazione di Al3+ in un acqua di scarico.
p. 345
190](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-190-320.jpg)



![194
Calcolare il potenziale del semielemento
Pt/chinone (0,03 M), idrochinone (0,01 M)
in HCl 0,1 M.
Esempi
]
(OH)
H
C
[
]
H
[
]
O
H
C
[
log
2
0591
,
0
699
.
0
V
2
4
6
2
2
4
6
Id
/
Ch
Il chinone ha formula C6H4O2; l’idrochinone ha formula C6H4(OH)2. La reazione
elettrodica è (App. 4 del testo):
C6H4O2 + 2H+ + 2e- = C6H4(OH)2 V° in HCl 1,0 M: 0,696 V
Le specie ossidate sono quelle a sinistra (acquistano elettroni e quindi si
riducono). Pertanto l’equazione di Nernst è:
V
654
.
0
01
.
0
)
10
(
03
.
0
log
2
0591
,
0
699
.
0
V
2
1
Id
/
Ch
](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-194-320.jpg)



























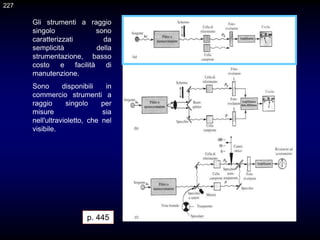
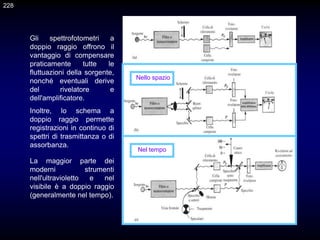
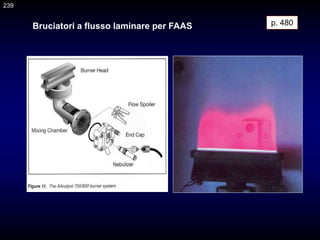
![Rivelazione del segnale
I rivelatori fotonici di più largo impiego sono i fotomoltiplicatori.
Schema di principio e struttura di un tubo fotomoltiplicatore. Il guadagno [(n di
elettroni prodotti)/(n di fotoni incidenti)] del fotomoltiplicatore aumenta con la
tensione applicata agli elettrodi (ma la vita media diminuisce).
p. 416
222](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-222-320.jpg)










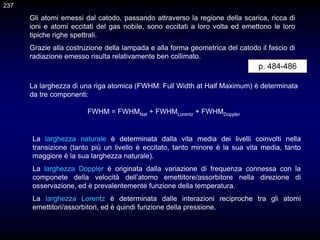










![PRINCIPI TEORICI DELLA CROMATOGRAFIA
Si consideri la separazione di un campione a tre componenti in una colonna chiusa.
La fase stazionaria consiste di particelle solide porose contenute all’interno di un tubo
lungo e sottile (colonna). Nel passaggio attraverso la colonna ogni componente X si
distribuisce fra la fase stazionaria (s) e la mobile (m):
Xm Xs
A: il campione viene iniettato
all’entrata della colonna
B D: la fase mobile fa spostare
il campione attraverso la fase
stazionaria
A B C D
Flusso
del
solvente
p. 518
m
s
X
[X]
[X]
K
Il coefficiente di ripartizione (o di distribuzione) del componente X è definito come:
Quale componente
ha K maggiore?
251](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-251-320.jpg)


























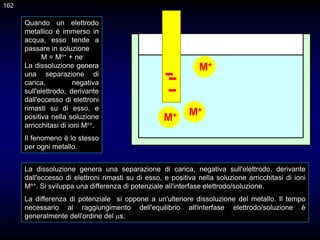
![Al fine di comprendere i principi di base delle tecniche in oggetto, è opportuno
considerare in dettaglio la struttura dell'interfase elettrodo/soluzione.
Si consideri un elettrodo immerso in una soluzione contenente le concentrazioni [R]b e
[O]b (il pedice b indica il bulk della soluzione e cioè l’intera massa) delle specie ridotta
ed ossidata, Rid ed Oss, rispettivamente, di una coppia d’ossidoriduzione. In base
alla semireazione
Oss + ne = Rid
possiamo scrivere l’Equazione di Nernst
in cui Voc (open circuit) è il potenziale dell’elettrodo a circuito aperto.
b
b
oc
]
R
[
]
O
[
log
n
059
,
0
V
V
281
Quando all’elettrodo è applicato un potenziale Vapp minore di Voc, per esempio Vapp = -
0,483 V, la concentrazione degli ioni cadmio all’interfase elettrodo soluzione, cioè nel
sottile strato di soluzione a contatto con la superficie elettrodica, deve ridursi in
accordo all’eq. di Nernst
M
10
.
0
,
2
C
V
483
,
0
)
C
log(
2
059
,
0
403
,
0
V 3
app
V
465
,
0
)
10
.
8
log(
2
059
,
0
403
,
0
V 3
oc
Nel caso l’elettrodo, per esempio un elettrodo a goccia di mercurio, sia immerso in
una soluzione di ioni cadmio a concentrazione 810-3 M, è facile verificare che il
potenziale elettrodico a circuito aperto è uguale a](https://image.slidesharecdn.com/desimoni2007-230719020439-fc626e1d/85/desimoni-2007-ppt-281-320.jpg)