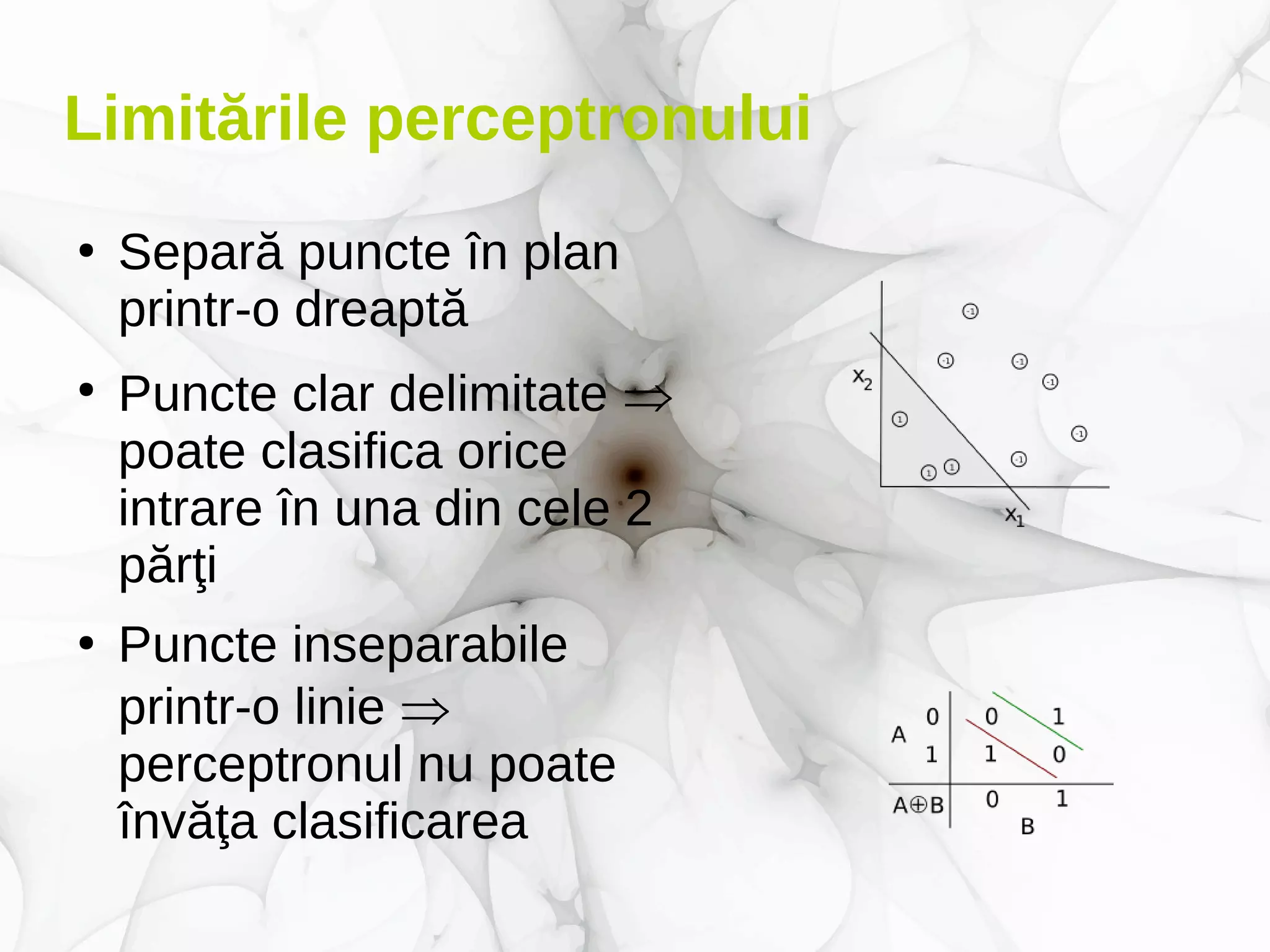
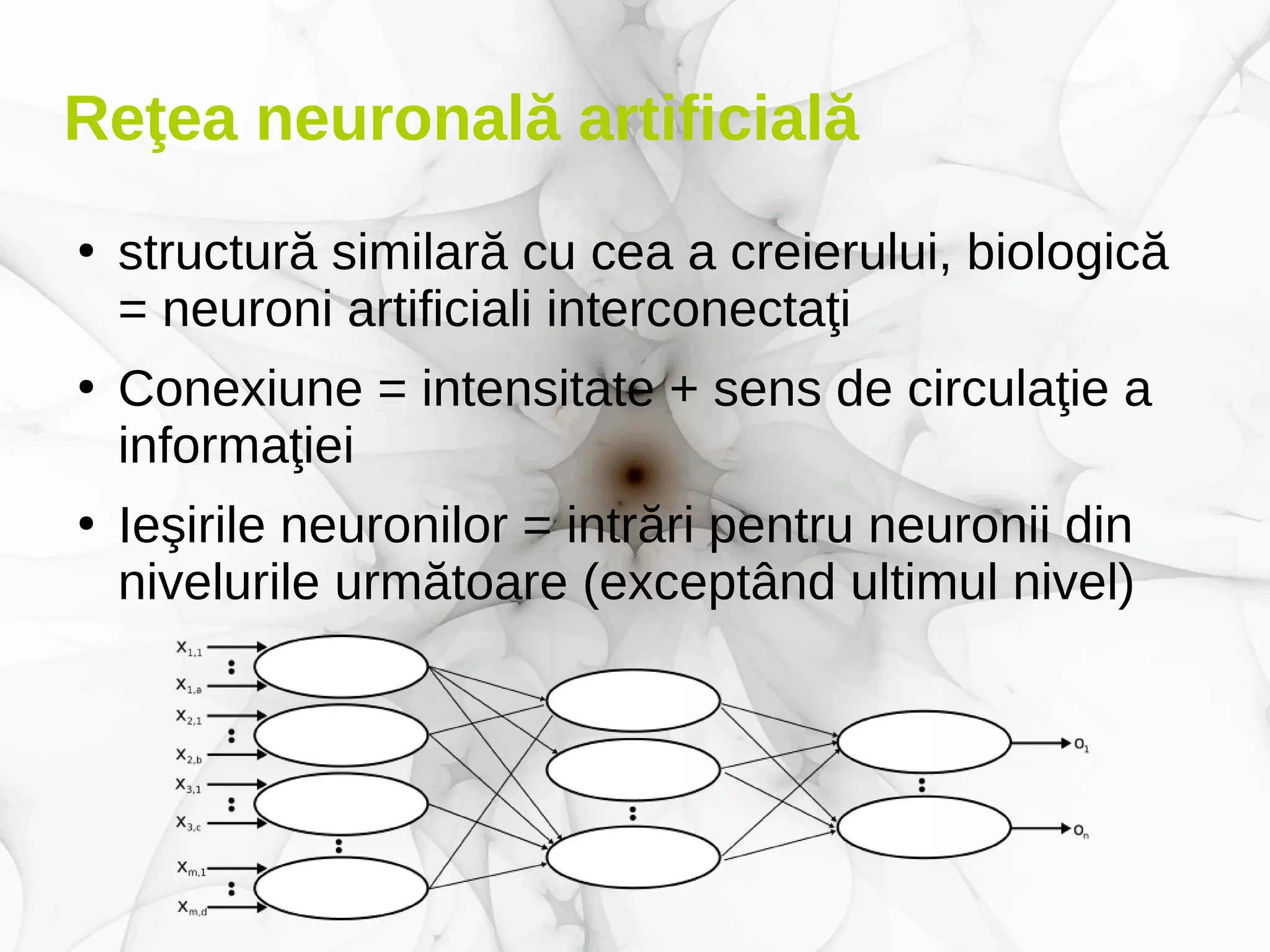
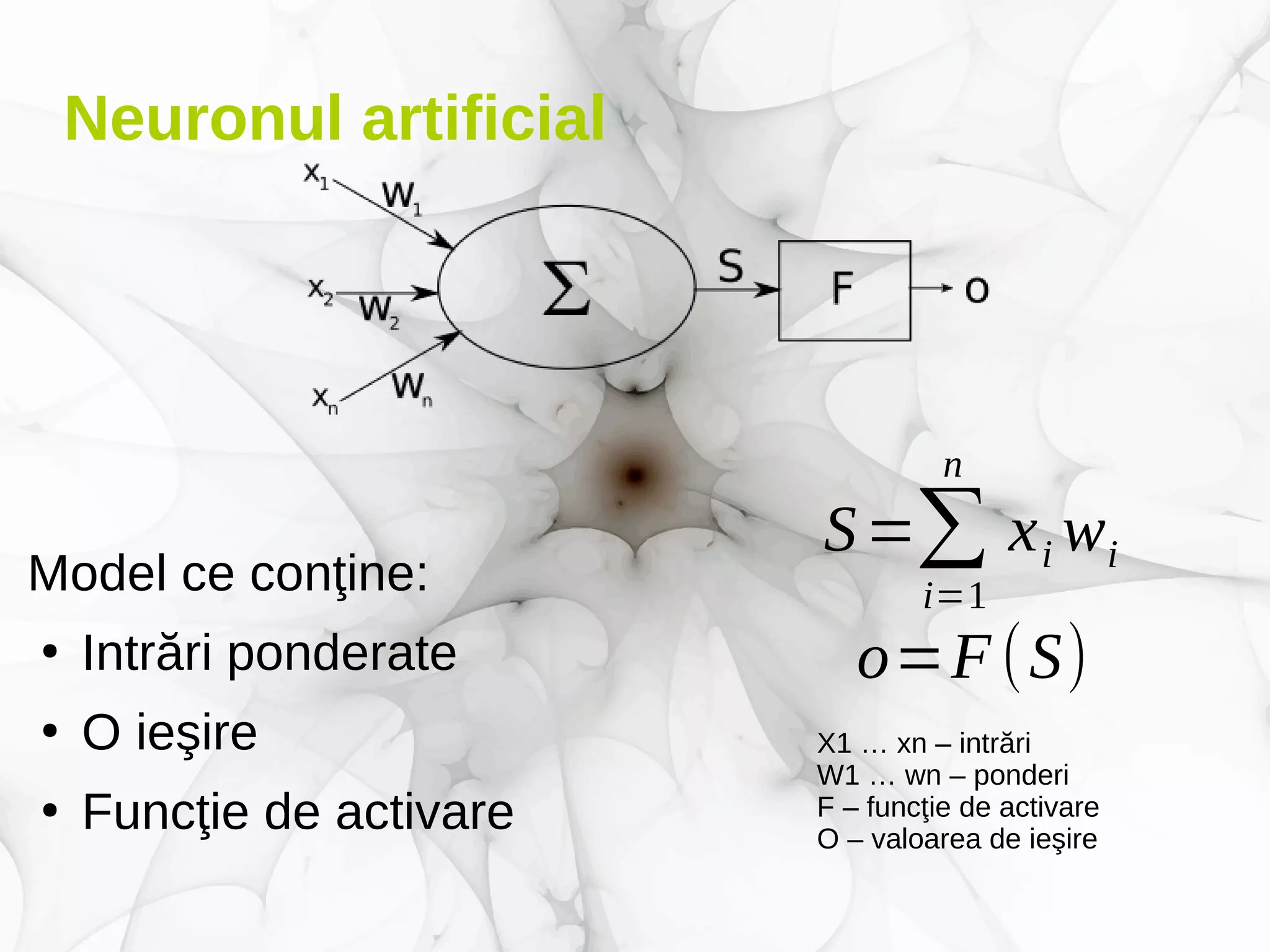
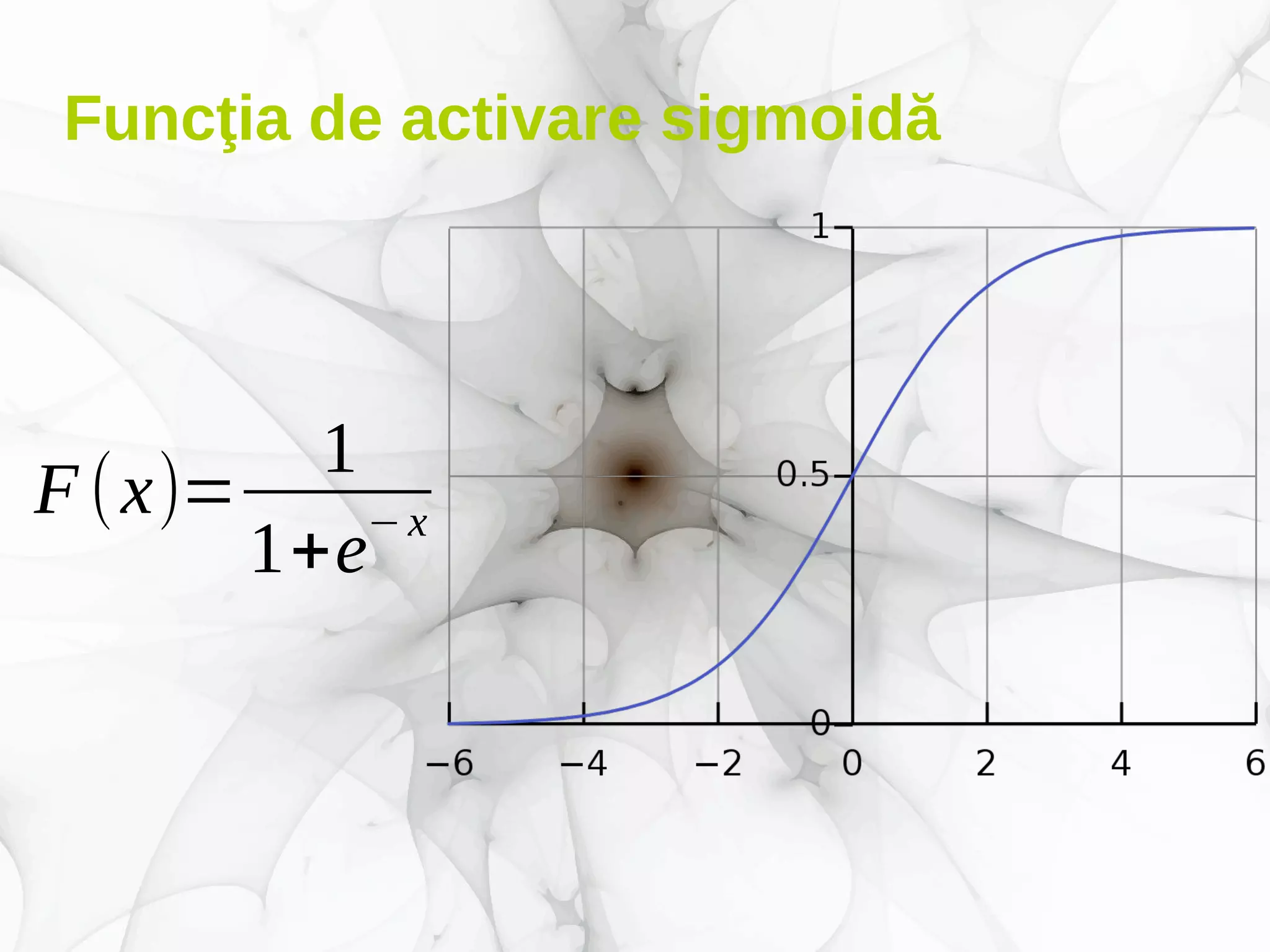
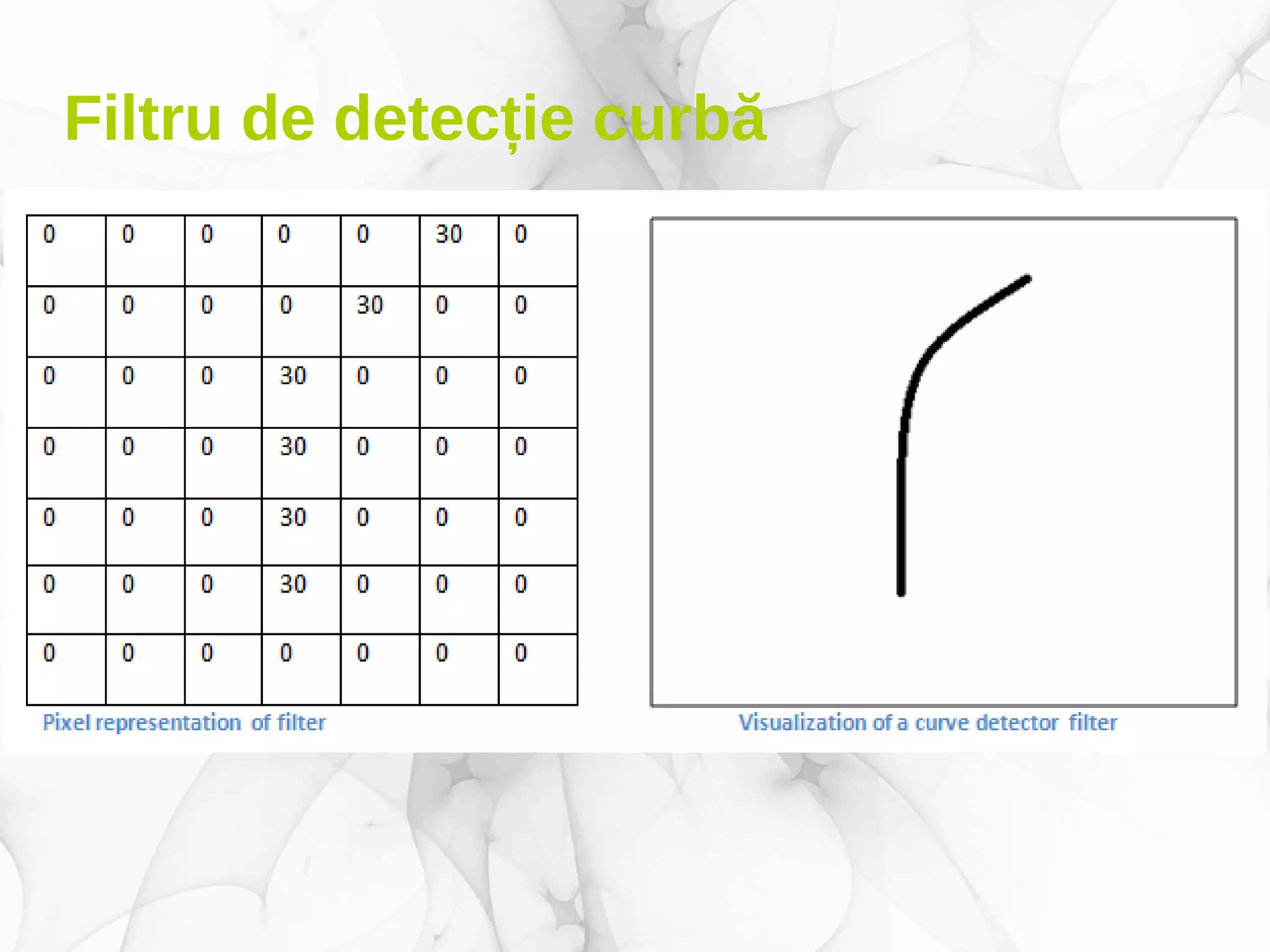
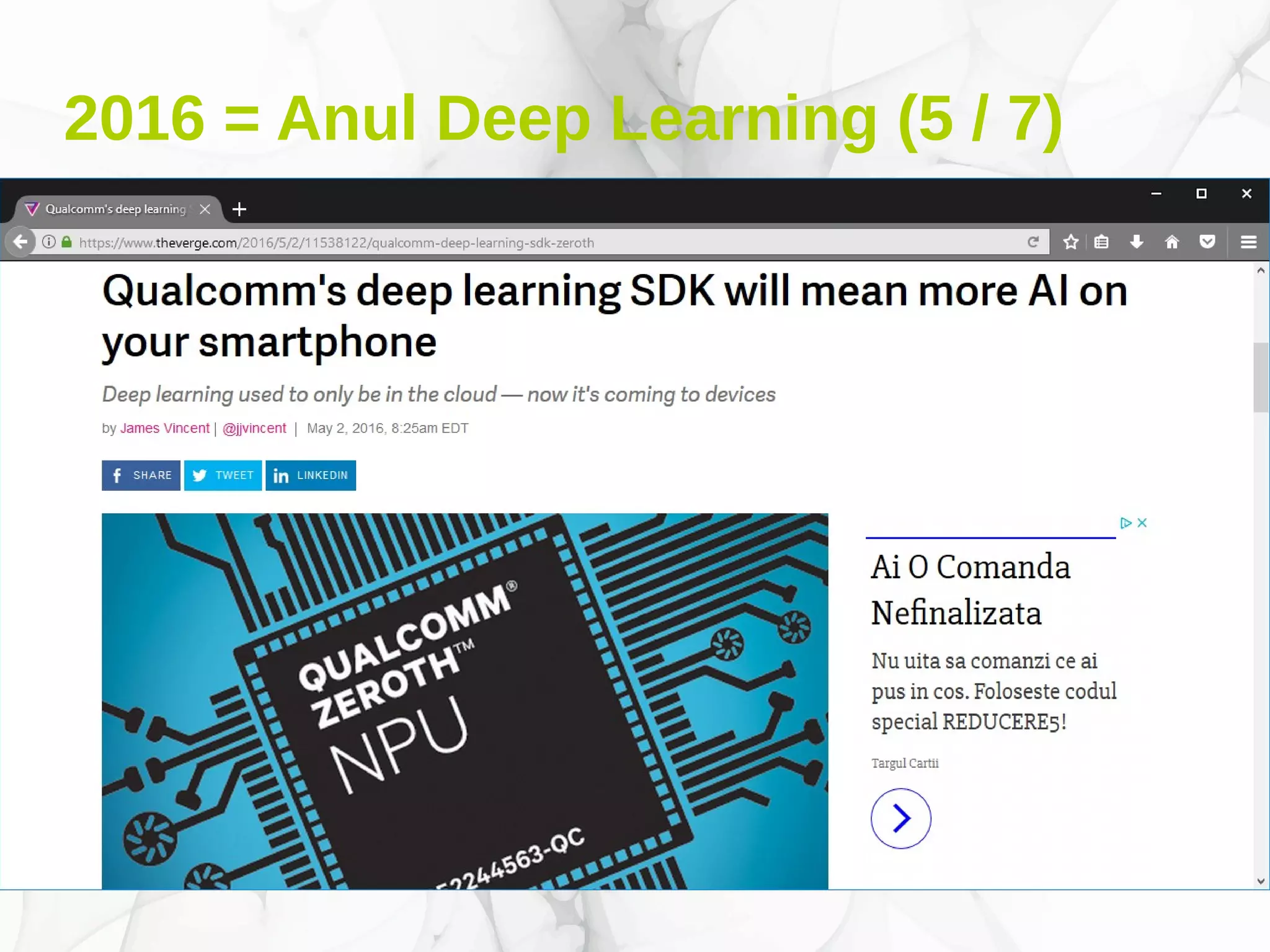
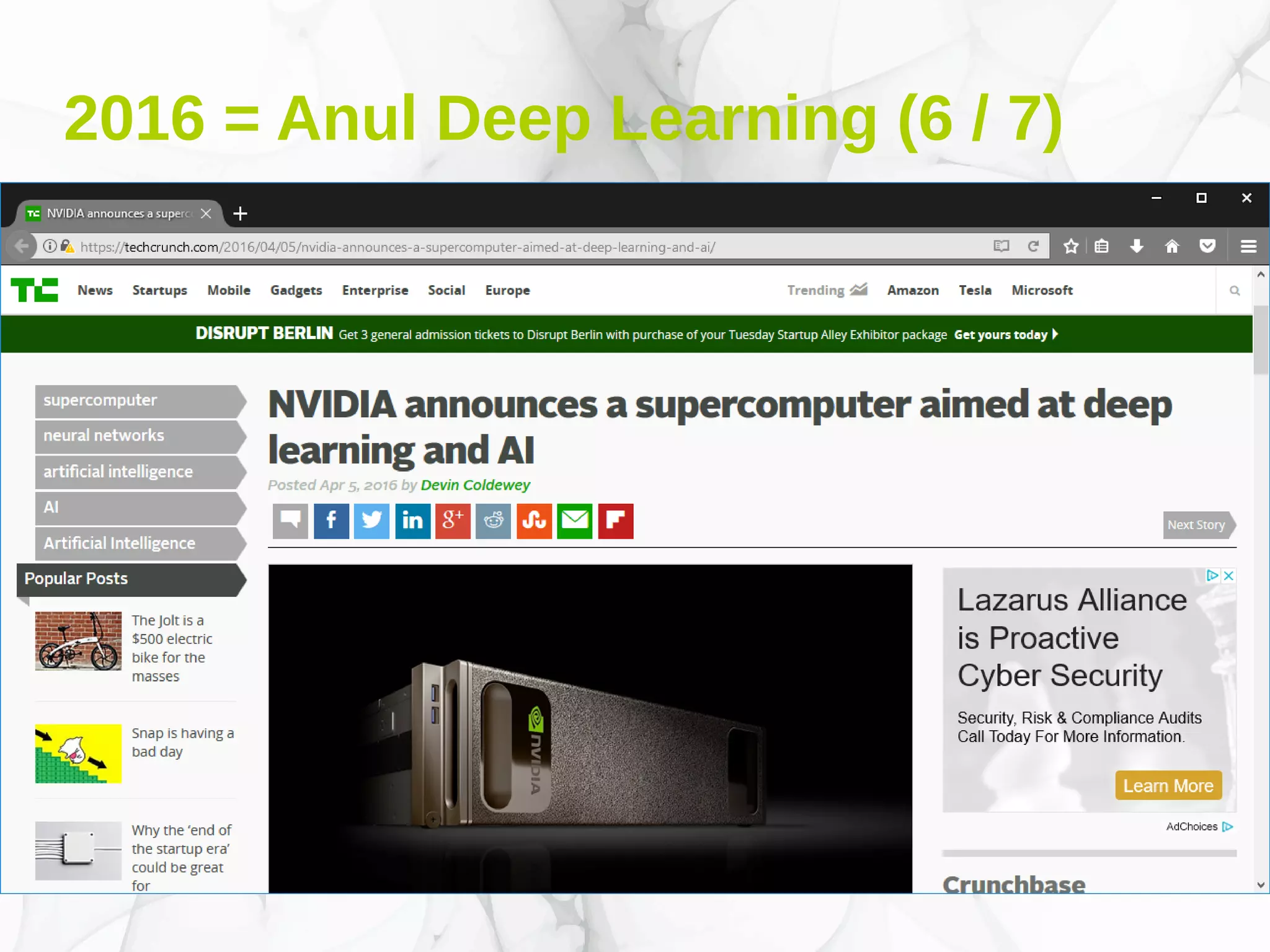
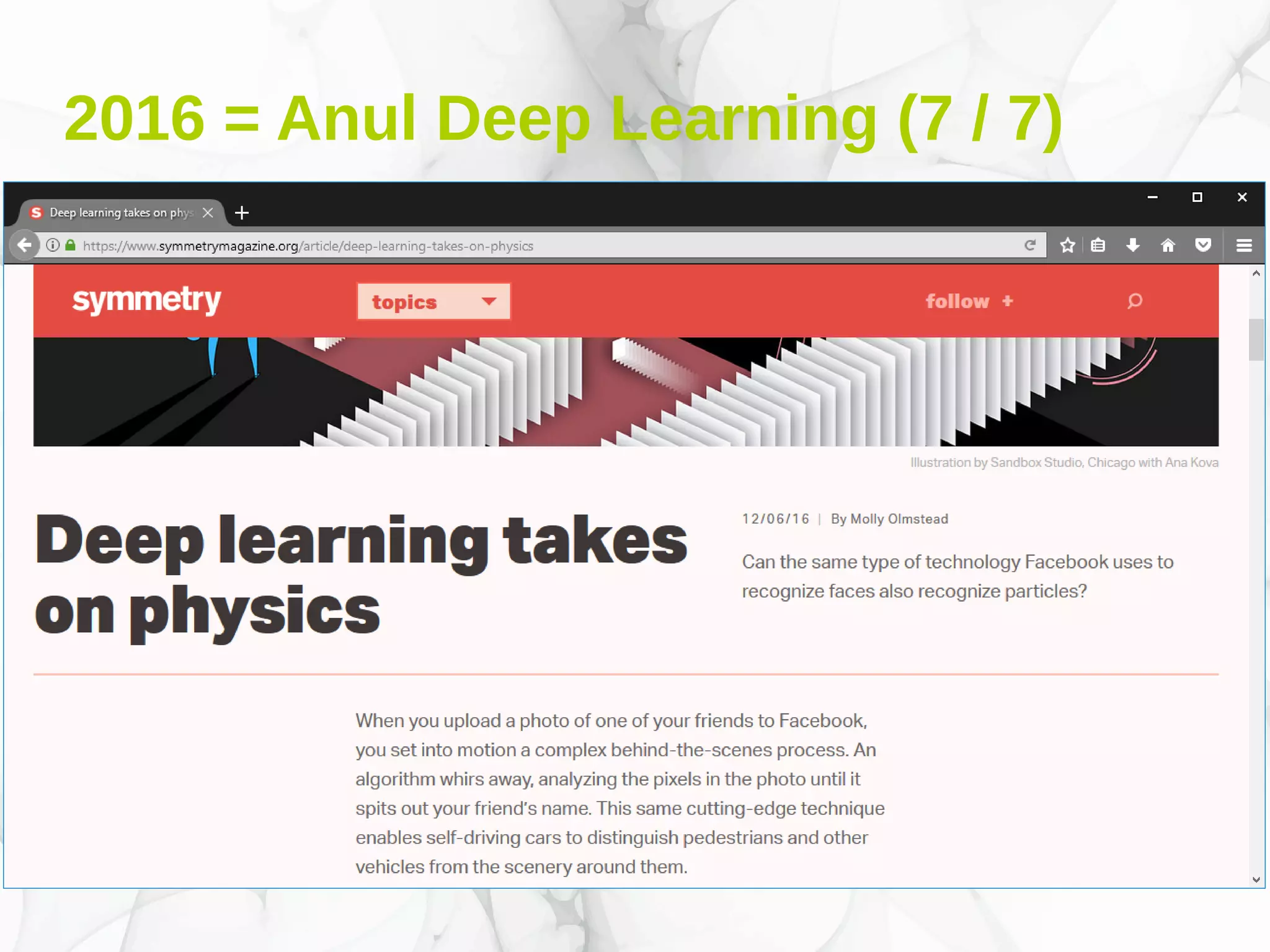
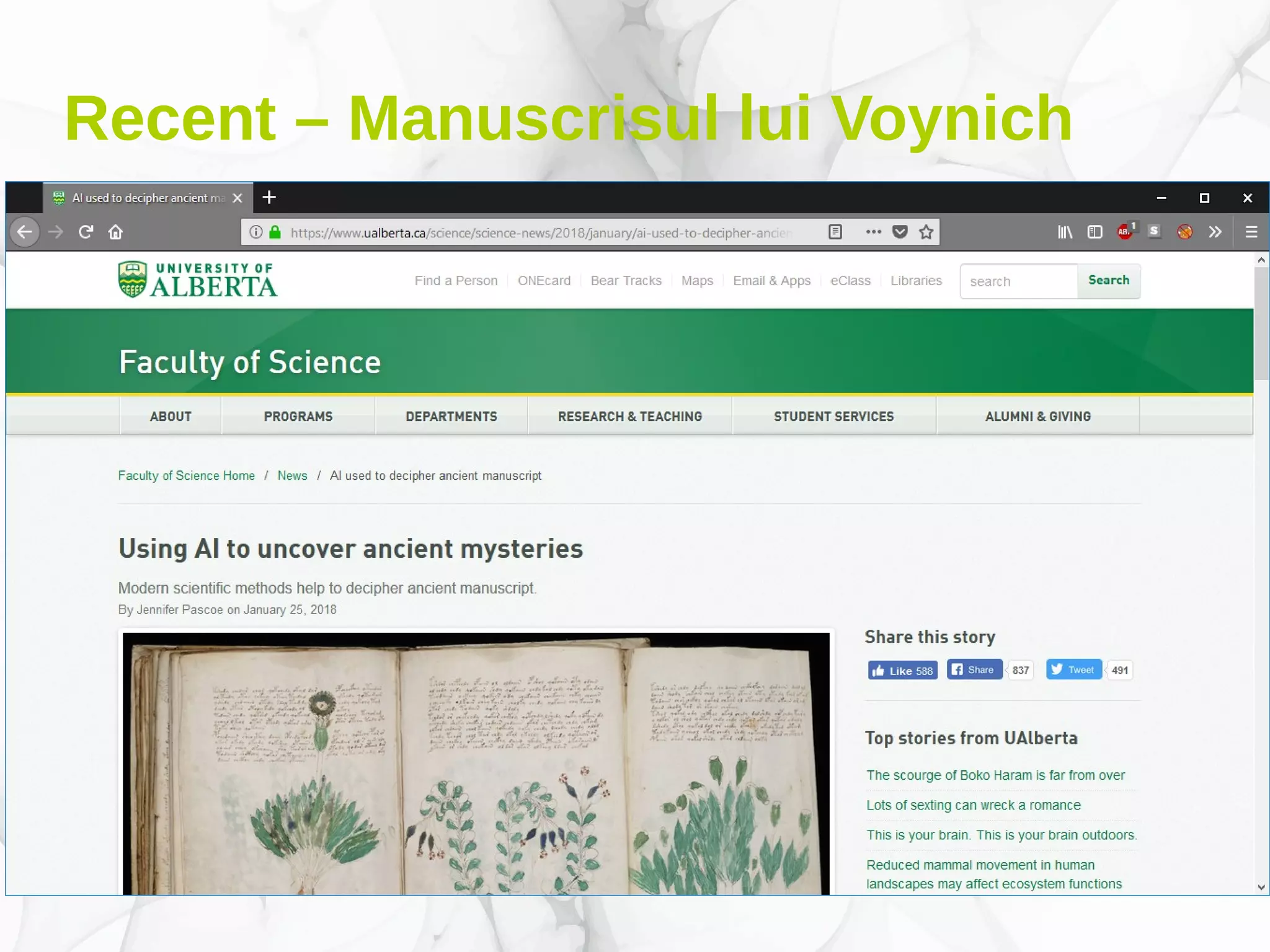
Documentul prezintă conceptele fundamentale și aplicațiile deep learning-ului, incluzând rețele neuronale, algoritmi de învățare, și tehnici de optimizare precum coborârea pe gradient. De asemenea, se discută despre rețele neuronale convoluționale și importanța volumului mare de date în antrenarea acestor modele. Este evidențiat rolul deep learning-ului în progresele recente din inteligența artificială și utilizarea sa în diverse domenii precum robotică și computer vision.

1. Deep Learning
Vlad Ovidiu Mihalca
- doctorand Computer Vision şi Inteligenţă Artificială -
Mecatronică @ Universitatea din Oradea
Ianuarie 2018

2. INDEX SESIUNI
Partea I: concepte şi fundamente teoretice
Partea II: frameworks şi utilizare practică
Partea III: aplicaţii în robotică şi Computer
Vision, direcţii de cercetare

3. CONCEPTE ŞI
FUNDAMENTE
TEORETICE
Partea I

4. ÎN ACEASTĂ SESIUNE
●
Despre Deep Learning. De ce acum?
●
Modele de învățare automată
●
Perceptronul
●
Rețele neuronale artificiale
●
Funcțiile de activare sigmoid, tanh, ReLU
●
Coborârea pe gradient
●
Propagarea înapoi
●
Despre rețele convoluționale
4/34

5. 2016 = Anul Deep Learning (1 / 7)

6. 2016 = Anul Deep Learning (2 / 7)

7. 2016 = Anul Deep Learning (3 / 7)

8. 2016 = Anul Deep Learning (4 / 7)

9. 2016 = Anul Deep Learning (5 / 7)

10. 2016 = Anul Deep Learning (6 / 7)

11. 2016 = Anul Deep Learning (7 / 7)

12. Recent – Manuscrisul lui Voynich

13. Deep Learning. De ce acum?
●
Ramură a inteligenţei artificiale, mai exact parte a
Machine learning
●
Metode bazate pe modele ce efectuează învăţare
●
Contrast cu algoritmii specific implementaţi
●
De ce doar acum a devenit subiect de vârf:
– Existenţa unor seturi de date foarte extinse
– Progres în GPU şi hardware, scăderea preţurilor
– Tehnici îmbunătăţite

14. Modele în deep learning
●
Creierul dispune iniţial de un model pentru
aproximarea realităţii, iar pe parcursul
dezvoltării umane primeşte impulsuri senzoriale
şi aproximează experienţa trăită.
●
Factorii externi (părinţii) confirmă sau infirmă
aproximarea noastră => modelul se întăreşte
sau este corectat
●
În machine learning, noţiunile de mai sus au
inspirat căutarea unor modele ajustabile care
să permită învăţarea prin exemple

15. Perceptronul liniar
●
Modelul: o funcţie h(x, θ)
– x este un vector al intrărilor în model
– θ este un vector de parametri interni modelului
●
Exemplu: un model de prezicere dacă vom
avea rezultate sub medie sau peste medie în
cazul unui examen, ştiind numărul de ore
dormite şi nr. de ore de studiu în pregătirea sa:
x=[x1, x2]T x1
– nr. ore dormite
x2
– nr. ore studiu
θ=[θ 1,θ 2,θ 0]T
h(x ,θ)=
{
−1dacă xT
⋅
[θ 1
θ 2]+θ 0<0
1dacă xT
⋅
[θ 1
θ 2
]+θ 0≥0

16. Limitările perceptronului
●
Separă puncte în plan
printr-o dreaptă
●
Puncte clar delimitate 
poate clasifica orice
intrare în una din cele 2
părţi
●
Puncte inseparabile
printr-o linie 
perceptronul nu poate
învăţa clasificarea

17. Reţea neuronală artificială
●
structură similară cu cea a creierului, biologică
= neuroni artificiali interconectaţi
●
Conexiune = intensitate + sens de circulaţie a
informaţiei
●
Ieşirile neuronilor = intrări pentru neuronii din
nivelurile următoare (exceptând ultimul nivel)

18. Neuronul artificial
Model ce conţine:
●
Intrări ponderate
●
O ieşire
●
Funcţie de activare
X1 … xn – intrări
W1 … wn – ponderi
F – funcţie de activare
O – valoarea de ieşire
S=∑
i=1
n
xi wi
o=F(S)

19. Tipuri de neuroni artificiali
●
Funcţia de activare folosită determină tipul
●
Funcţie liniară => reţeaua se reduce la
perceptron
●
Funcţia de activare introduce neliniaritate
●
Sunt uzuale trei tipuri de neuroni:
– Sigmoid
– Tanh (tangentă hiperbolică)
– ReLU (Rectifier Linear Unit)

20. Funcţia de activare sigmoidă
F(x)=
1
1+e
−x

21. Funcţia de activare tangentă
hiperbolică
F(x)=tanh(x)=
ex
−e−x
e
x
+e
−x

22. Funcţia de activare rampă (ReLU)
F(x)=max(0,x)

23. Procesul de învăţare
●
Ajustarea ponderilor conexiunilor în mod
iterativ, pentru a oferi soluţiile dorite
●
Mai multe tipuri de tehnici şi algoritmi
●
Algoritmul de propagare înapoi: deplasarea pe
nivelurile anterioare a diferenţei dintre rezultat
şi obiectiv

24. Algoritmul de propagare înapoi
1)Aplicarea unui vector la intrare => rezultat la
ieşire
2)Compararea ieşirii cu vectorul dorit
3)Diferenţa se propagă înapoi în reţea
4)Ajustarea ponderilor conform unui algoritm ce
minimizează eroarea

25. Funcţia eroare
Presupunând t(i) răspunsul corect pentru al i-lea
exemplu şi y(i) ieşirea reţelei => funcţia eroare:
E=
1
2
∑i
(t
(i)
−y
(i)
)
2
Minimizarea erorii = problemă de optimizare
=> tehnici diverse de optimizare:
●
Coborâre pe gradient (abordare tipică)
●
Algoritmi genetici
●
Algoritmi din swarm intelligence (PSO, ACO, GSO..)

26. Coborârea pe gradient
●
Planul XY – dat de ponderi (de ex. w1 şi w2)
●
Pe Z: val. erorii în punctul cu ponderile resp.
=> ne situăm pe suprafaţa generată, undeva
●
Dorim să coborâm panta spre un minim
●
Panta cea mai abruptă = perpendiculara pe
curba de nivel => calea minimă = coborârea pe
gradientul funcţiei eroare
Calculăm: Δ wk=−ϵ
∂ E
∂wk
=...=∑
i
ϵ xk
(i)
(t
(i)
− y
(i)
)
ϵ = rata de învăţare (hiperparametru) xk(i) = al k-lea input din al i-lea exemplu
i = al i-lea exemplu de învăţare t(i),y(i) = răspunsul corect / ieşirea

27. Coborârea pe gradient - vizual

28. Propagarea înapoi şi coborârea în
gradient
Cum ajustăm ponderile într-o reţea cu nivel
ascuns?
- determinăm cum se schimbă eroarea în funcţie
de ieşirile ascunse
- ulterior putem determina cum se schimbă în
funcţie de o pondere individuală
=> abordare de programare dinamică

29. Rețele neuronale convoluționale
●
Rețelele neuronale clasice – foarte dense
pentru imagini
●
Simplificăm graful – calculăm un subgraf
●
Filtre multiple sunt aplicate asupra părți din
imagine, repetitiv
●
Operația se numește convoluție
●
Convoluție = operație liniară => neliniaritate
adăugată de ReLU
●
Rețeaua neuronală se antrenează pe aceste
hărți de trăsături

30. Termeni
●
Filtru = matrice suprapusă
●
Câmp receptor = subzona de interes din
imagine
●
Parametri = valorile din filtru
●
Convoluție = aplicarea repetată a filtrului
●
Hartă de trăsături / hartă de activare = matricea
rezultat a operațiilor

31. Hartă de activare (de trăsături)

32. Filtru de detecție curbă

33. Precizare în concluzie
Secretul aplicării cu succes a rețelelor neuronale
în practică:
Volum mare de INFORMAȚII.
=> de aceea au un mare avantaj competitiv
companii precum Facebook, Google, Instagram,
Pinterest, Amazon...

34. Bibliografie
●
Curs MIT 6.S191: Intro to Deep Learning
●
Nikhil Buduma – Fundamentals of Deep
Learning
●
Ecaterina Vladu – Inteligenţa artificială
●
Wikipedia. Deep learning
●
Adit Deshpande - A Beginner's Guide To
Understanding Convolutional Neural Networks