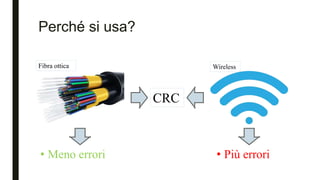
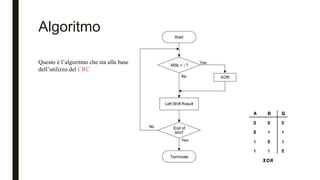
Il documento tratta del Controllo di Ridondanza Ciclica (CRC), un metodo utilizzato per rilevare errori nella trasmissione dei dati attraverso checksum. Descrive l'algoritmo di implementazione e fornisce esempi pratici per calcolare il CRC associato a un messaggio trasmesso. Infine, include riferimenti bibliografici per ulteriori approfondimenti sull'argomento.

1. CRC
(CYCLIC RENDUNDACY CHECK)
Di Laxman Cozzarin
26/12/2018

2. Indice
Cos’è
Perché si usa?
Comunicazione
Utilizzo
Algoritmo
Esempio
Bibliografia
Fine

3. Cos’è?
English:
Cyclic
Redundacy
Check
Italiano:
Controllo
Ridondanza
Ciclico
 Utilizzato per la stima degli errori
 È un metodo per il calcolo di somme di controllo
(checksum in inglese)
 Implementazione binaria
 Richiede conoscenze matematiche modeste
In telecomunicazioni e informatica il checksum (tradotto letteralmente significa somma di controllo)
è una sequenza di bit che, associata al pacchetto trasmesso, viene utilizzata per verificare l'integrità di
un dato o di un messaggio che può subire alterazioni durante la trasmissione sul canale di
comunicazione.

4. Comunicazione
Sorgente Trasmittente Canale Ricevitore Destinatario
messaggio Segnale
inviato
Segnale
inviato
messaggio
 messaggio: composto da segnali ottici, acustici, elettrici ecc.;
 trasmettitore: l’oggetto che invia il messaggio (telefono, computer, modem ecc.);
 ricevitore: lo strumento che legge e decodifica il msg
 canale: il mezzo attraverso il quale viene trasmesso il segnale (fili, onde radio,
luce);
 codice: l’insieme dei simboli impiegati per adattare il messaggio alla
trasmissione;
 protocollo: l’insieme delle regole che definiscono il formato dei messaggi stessi,
la loro lunghezza ecc.

5. Perché si usa?
Fibra ottica Wireless
• Meno errori • Più errori
CRC

6. Algoritmo
Questo è l’algoritmo che sta alla base
dell’utilizzo del CRC

7. Esempio
 M = messaggio da trasmettere esempio di valore: 1010 0011 1010 1100
 G = polinomio generatore esempio di valore: 11010
 M' = messaggio con associato il CRC
 CRC = M / G. (messaggio da trasmettere / polinomio generatore)
CRC = resto di M / G dove ad M sono stati concatenati n bits nulli (0) corrispondenti al grado di G.
 Se G = 11010 grado 4 perciò G(bit)=4 quindi si tratta di aggiungere 4 bits 0 ad M.
M = 1010 0011 1010 1100 0000.
Continua …
^ = elevato a potenza
G = 10101 = 1*2^4 + 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 =
= 2^4 + 2^3 + 2 = 26 grado di G è 4

8. Esempio
 1010 0011 1010 1100 0000
 1101 0||| MSB = 1 cominciamo subito con la sottrazione
 0111 0||| resto dopo aver effettuato la XOR
 111 00|| portiamo giù la prossima cifra MSB = 1 facciamo nuovamente la sottrazione
 110 10|| facciamo la sottrazione
 001 10|| resto dopo aver effettuato la XOR
 01 101| portiamo giù la prossima cifra MSB = 0 non facciamo la sottrazione e portiamo giù un
altro bit
 1 1011 MSB = 1 facciamo nuovamente la sottrazione
1 1010
 0 0001 resto dopo aver effettuato la XOR
Continua …

9. Ripeto…
1010 0011 1010
1100 0000
1101 0
0111 00
110 10
001 101
01 1011
1 1010
0 0001 1
0001 10
001 101
01 1010
1 1010
0 0000 1
0000 11
000 110
00 1100
0 1100 0
1101 0
0001 00
001 000
01 0000
1 1010
0 1010 == CRC
Per creare M' basta concatenare il CRC così ottenuto, ai bits del
messaggio da trasmettere M :
M' = 1010 0011 1010 1100 + 1010
M' = 1010 0011 1010 1100 1010

10. Bibliografia
 Autori: Andrew S. Tanenbaum, David J. Wetherall
 Libro: Reti di calcolatori
 Autore: Fabrizio Scorzoni
 Libro: Sistemi di Elaborazione
 Wikipedia (alcune definizioni semplificate)
 Google per le immagini

11. Grazie per l’attenzione e spero che vi sia piaciuto
Laxman Cozzarin