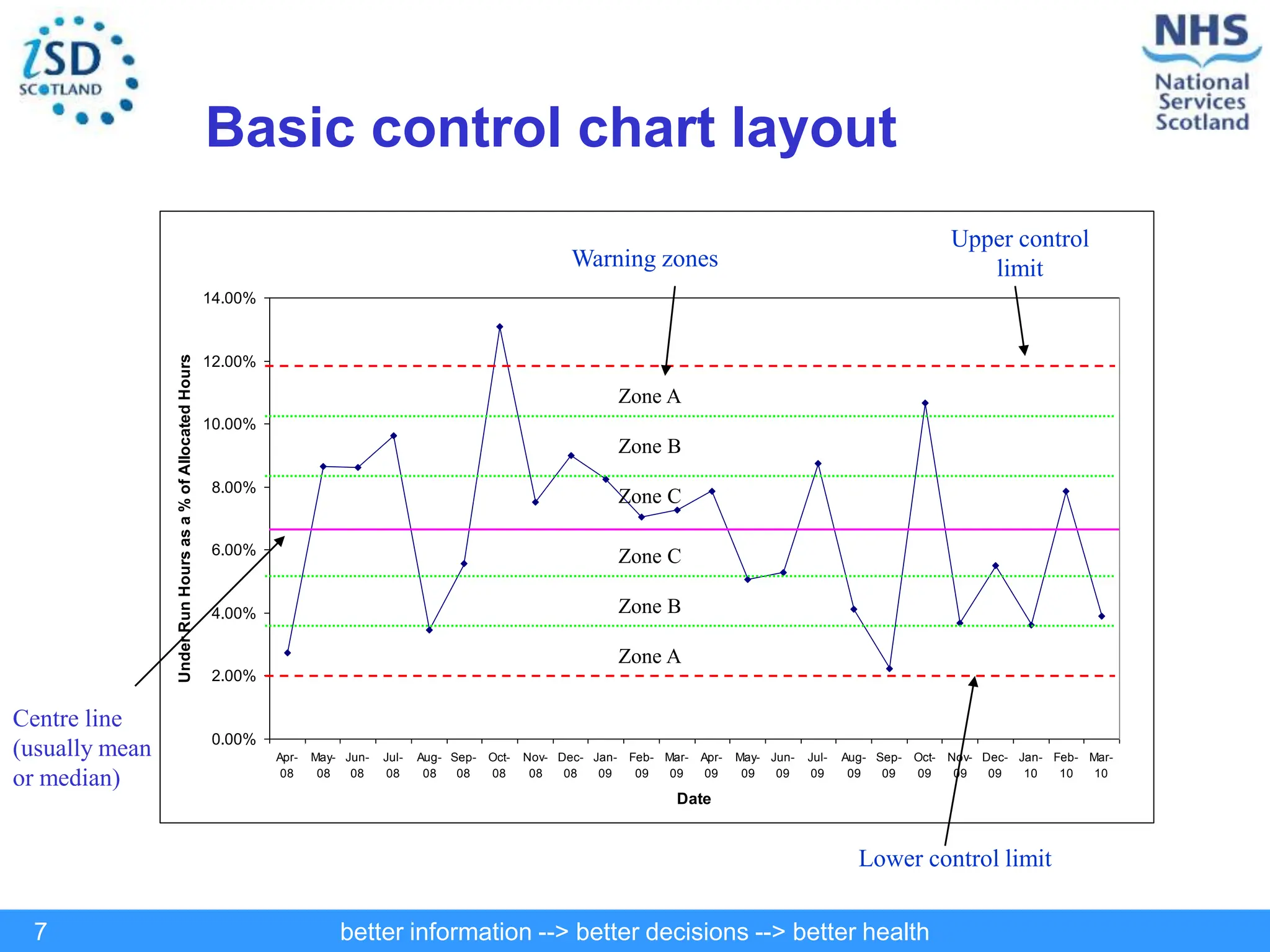
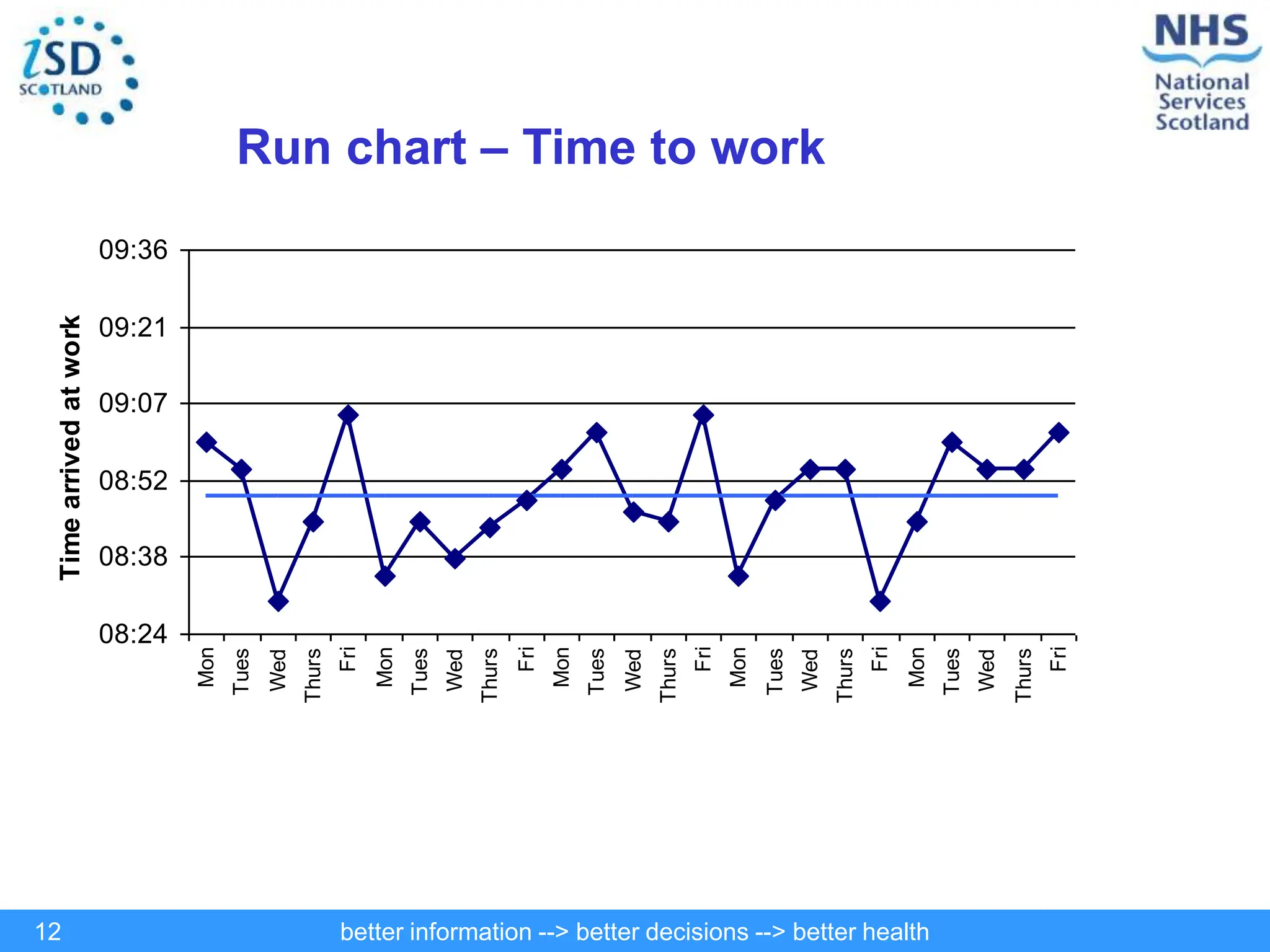
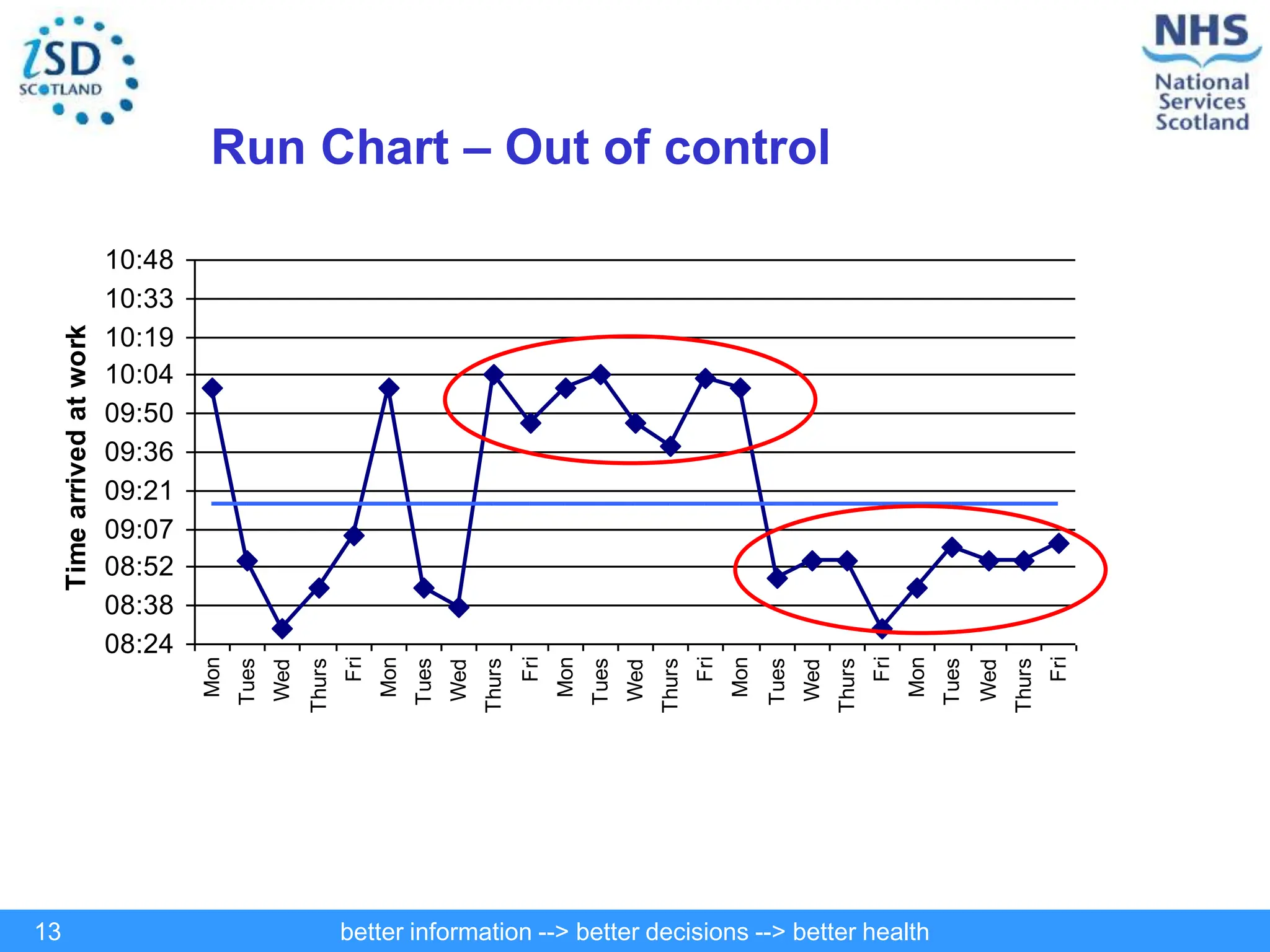
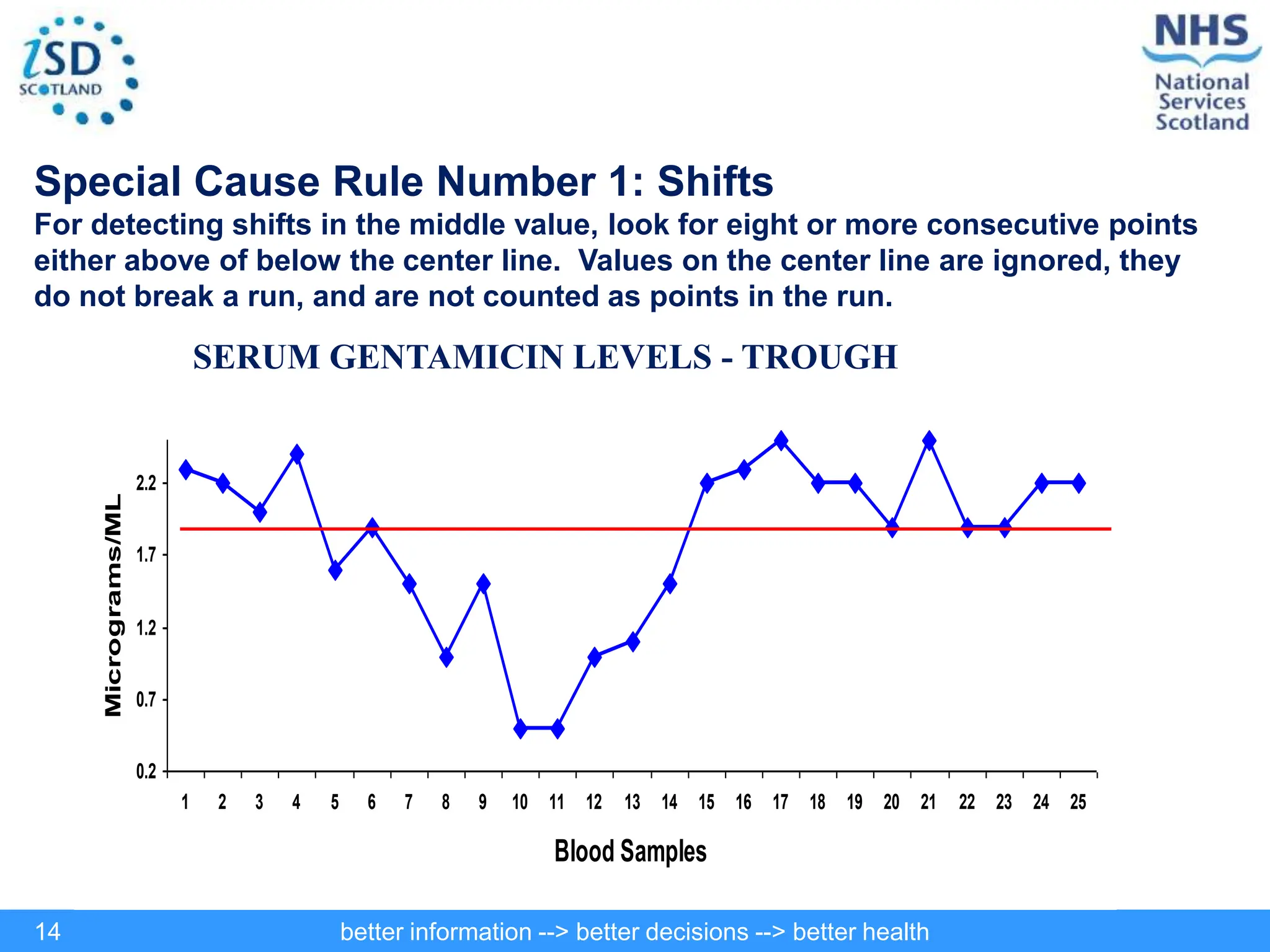
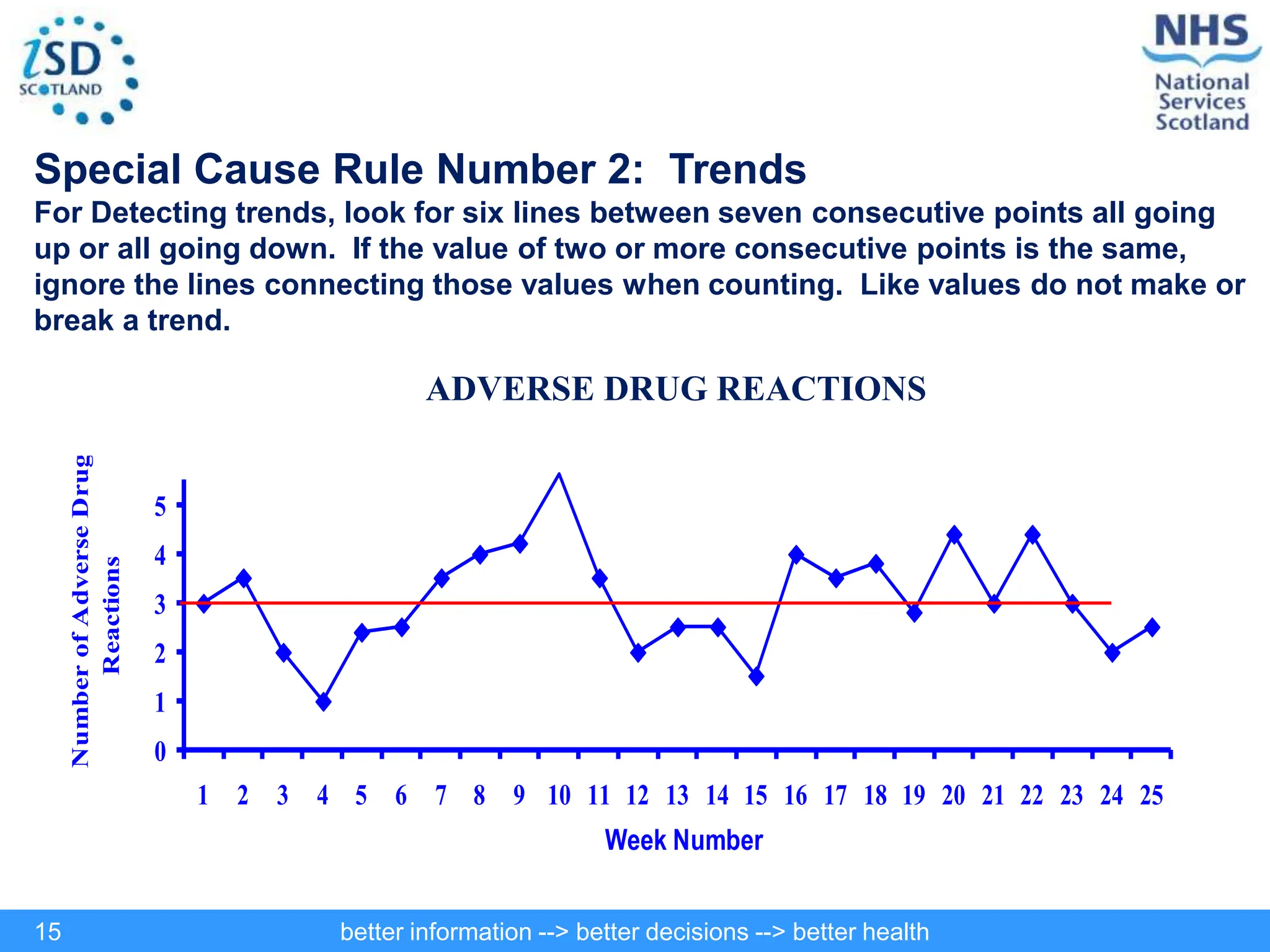
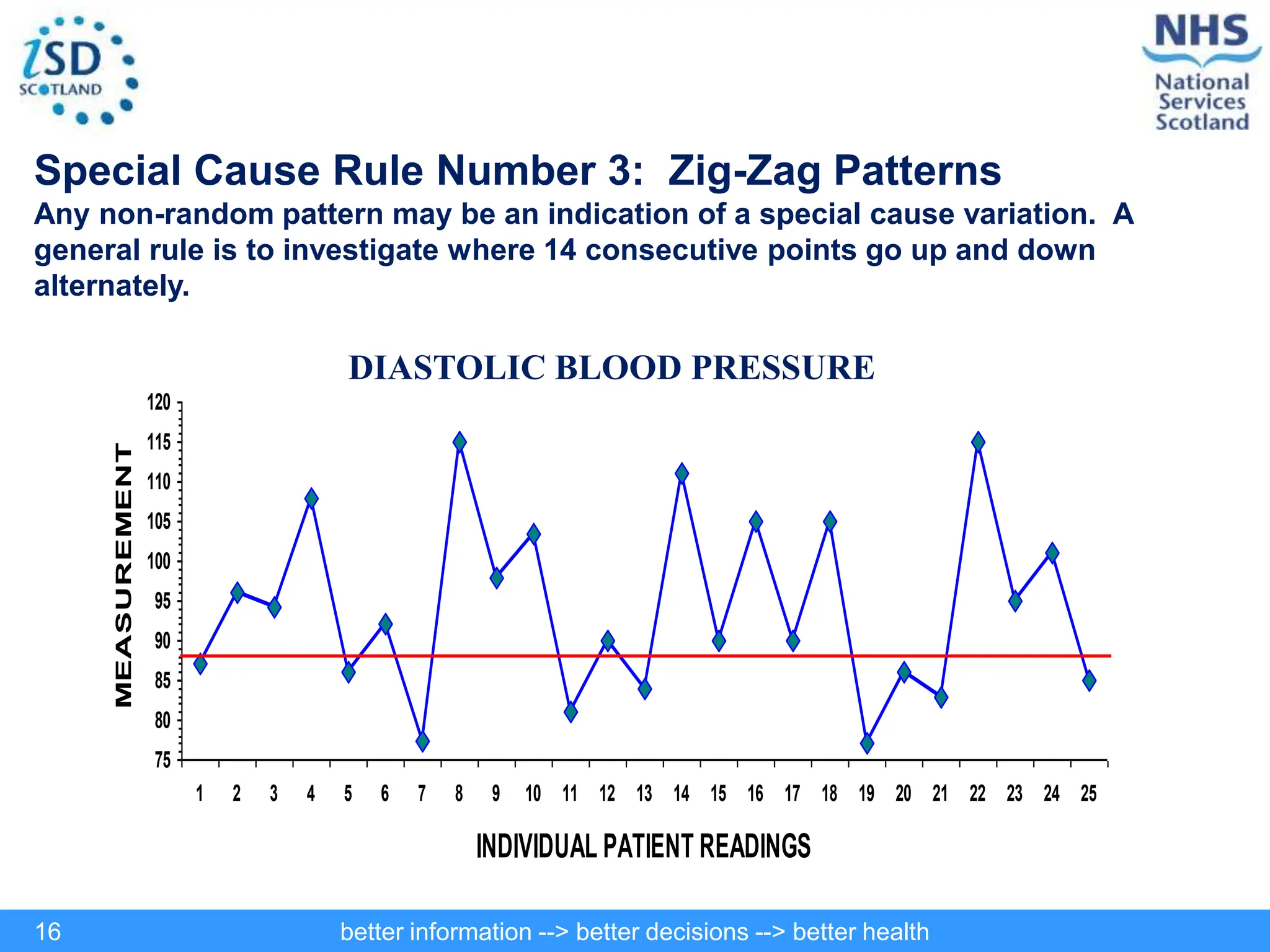
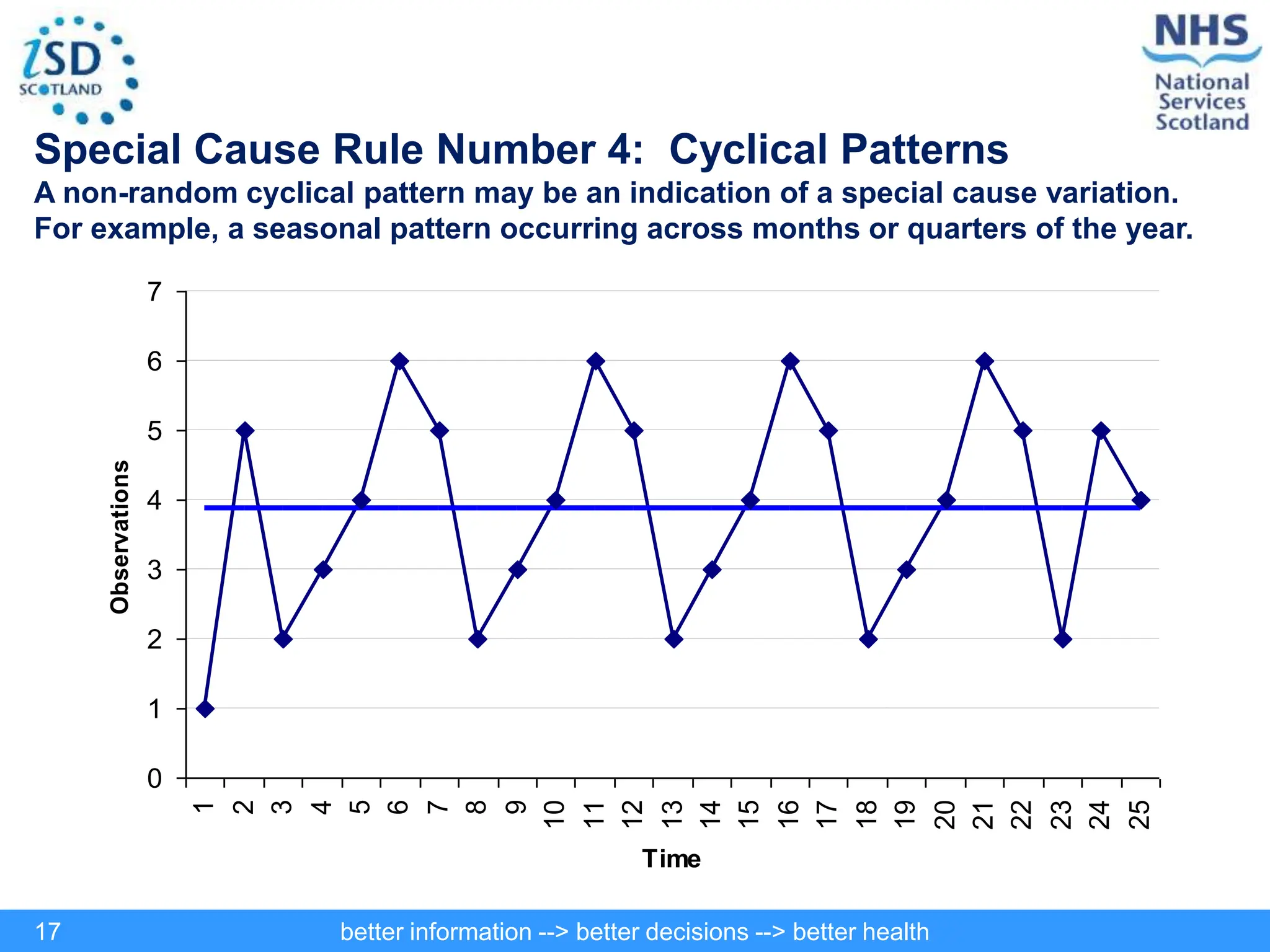
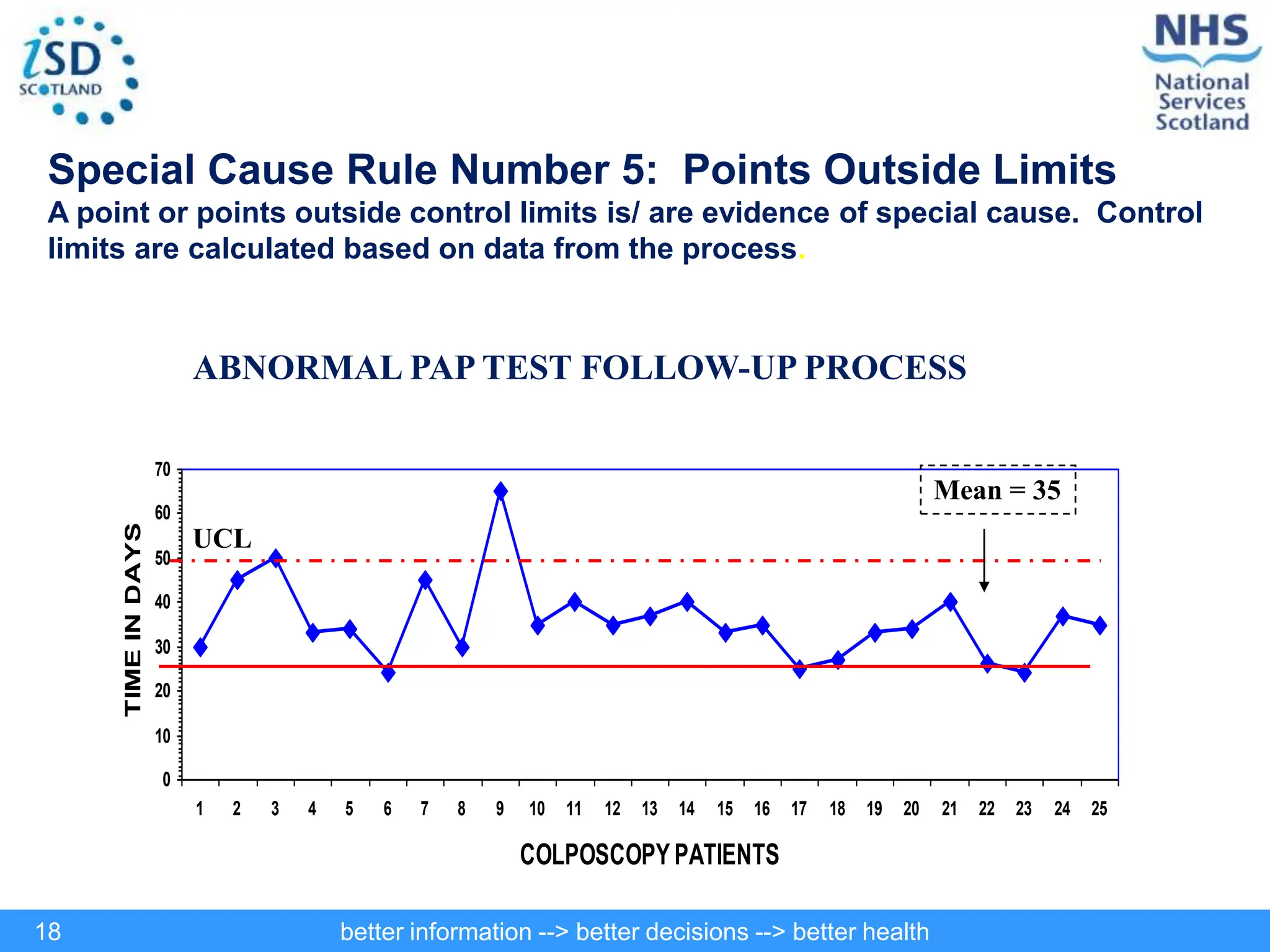
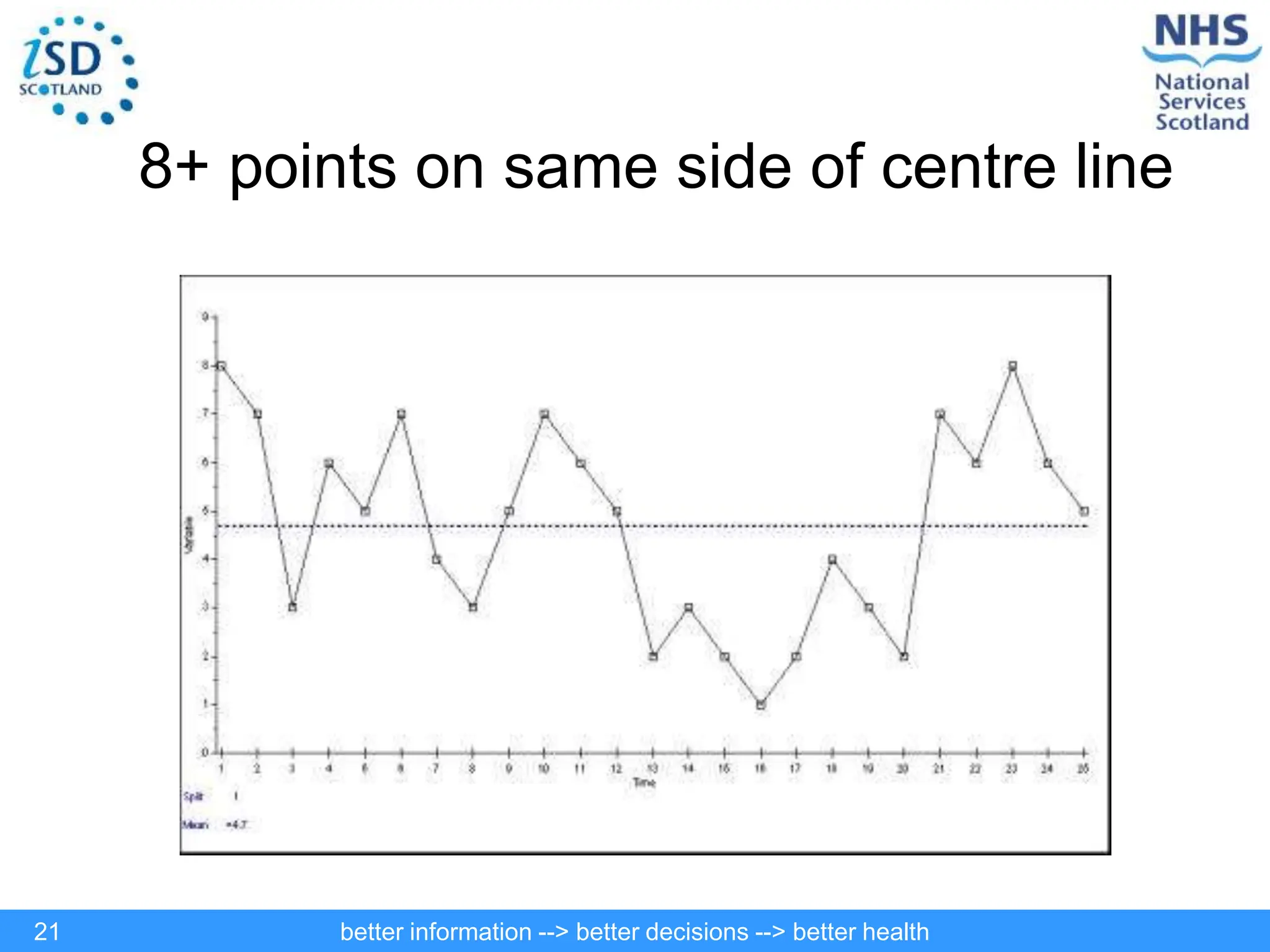
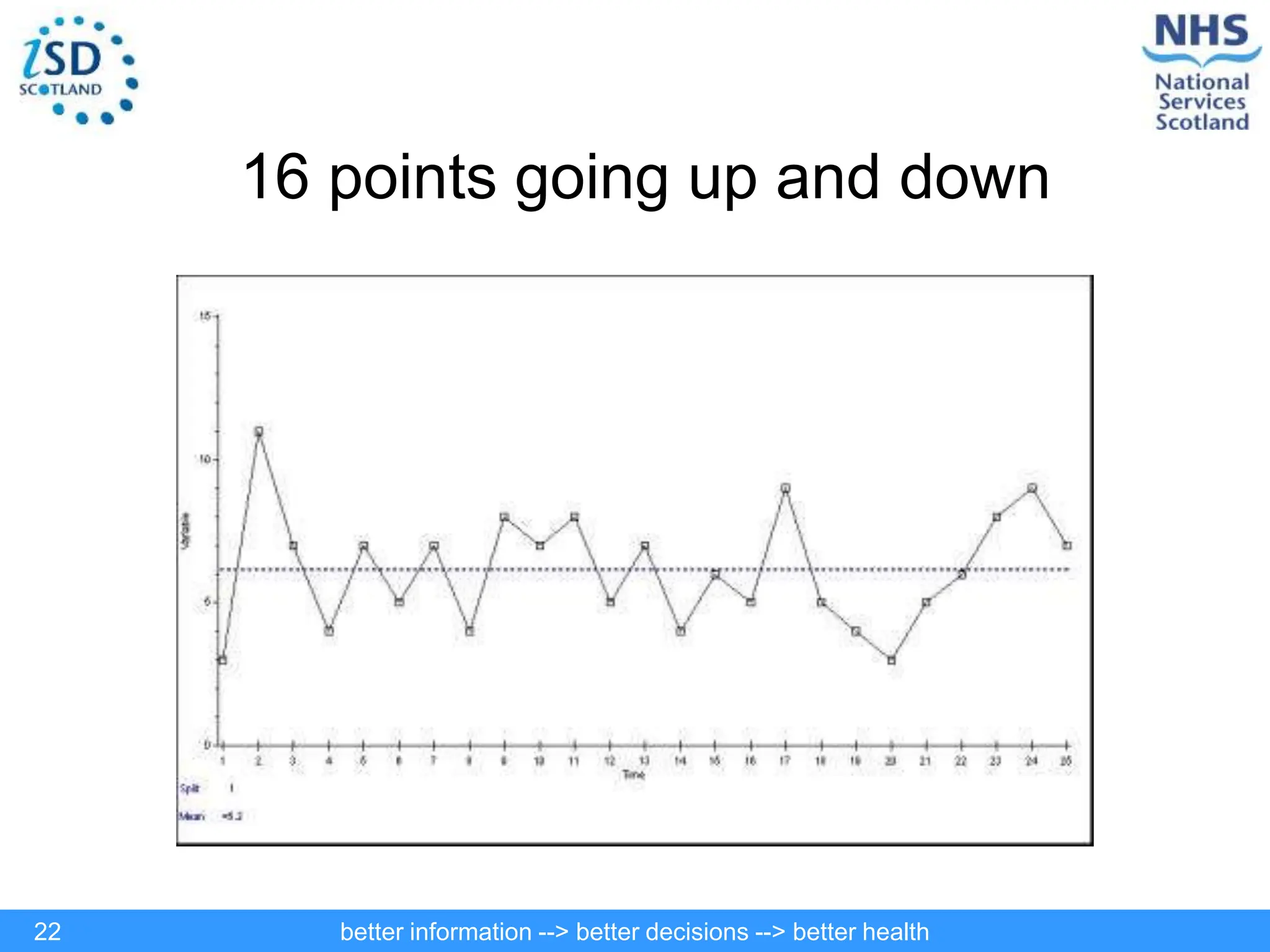
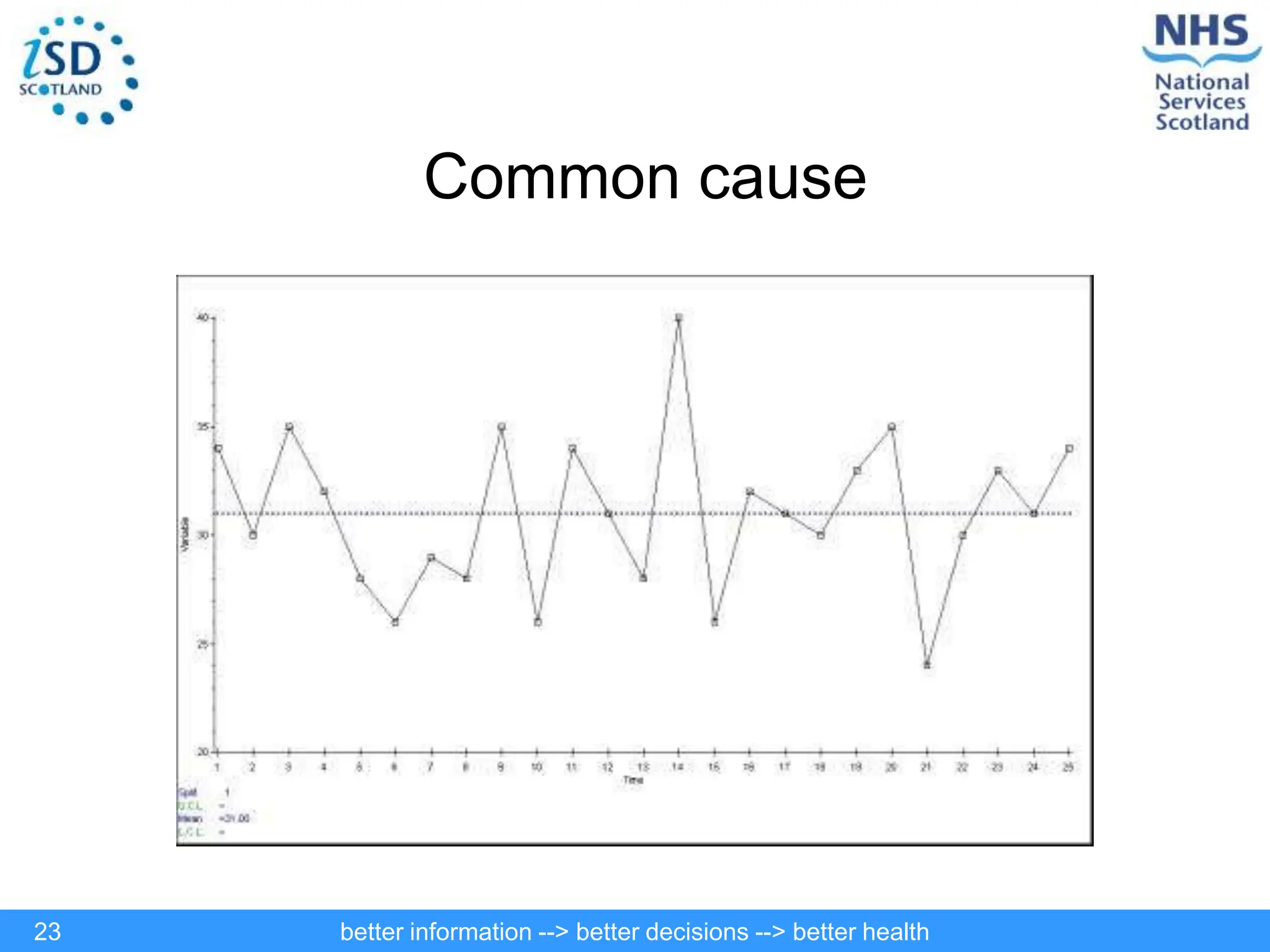
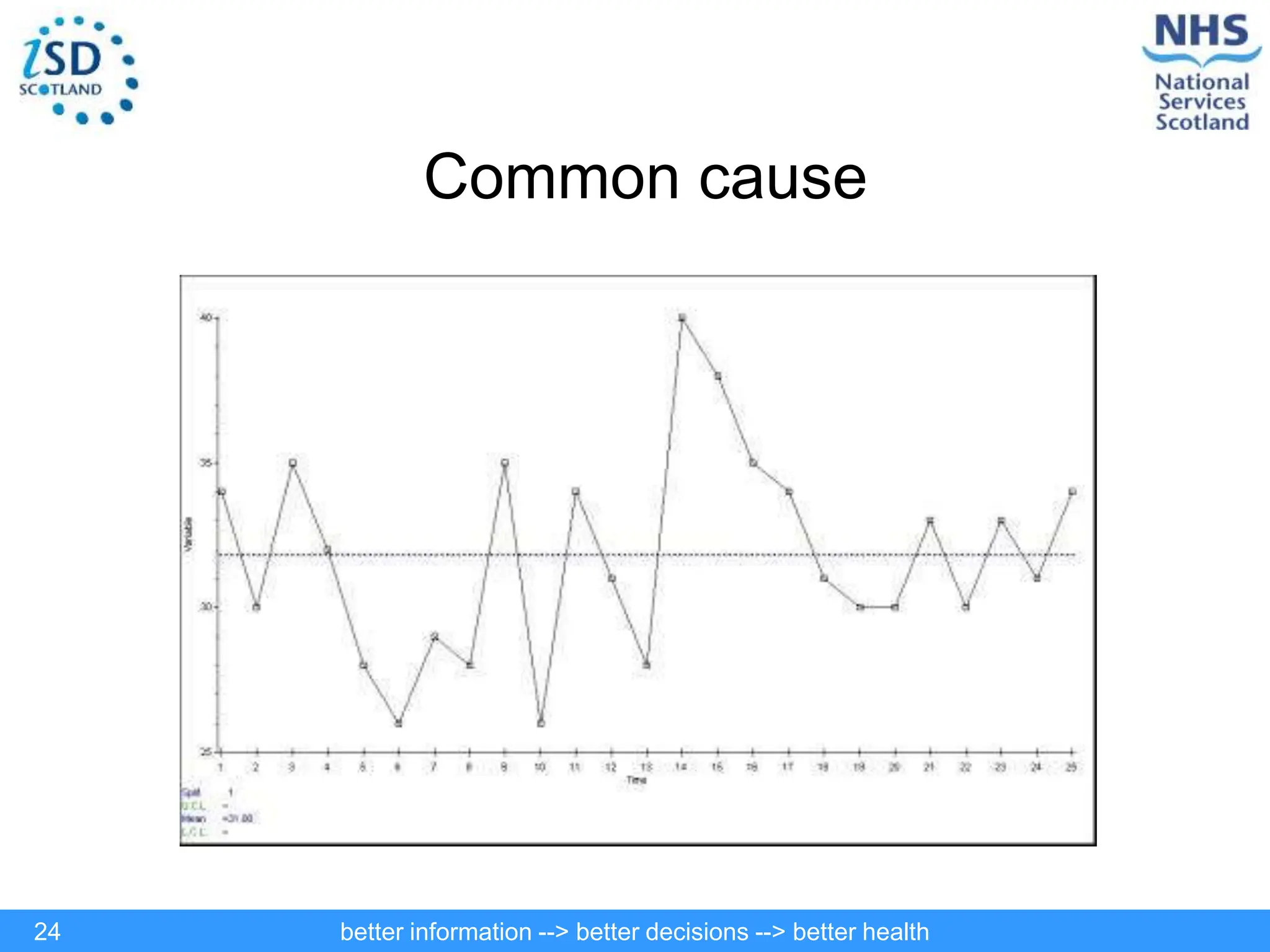
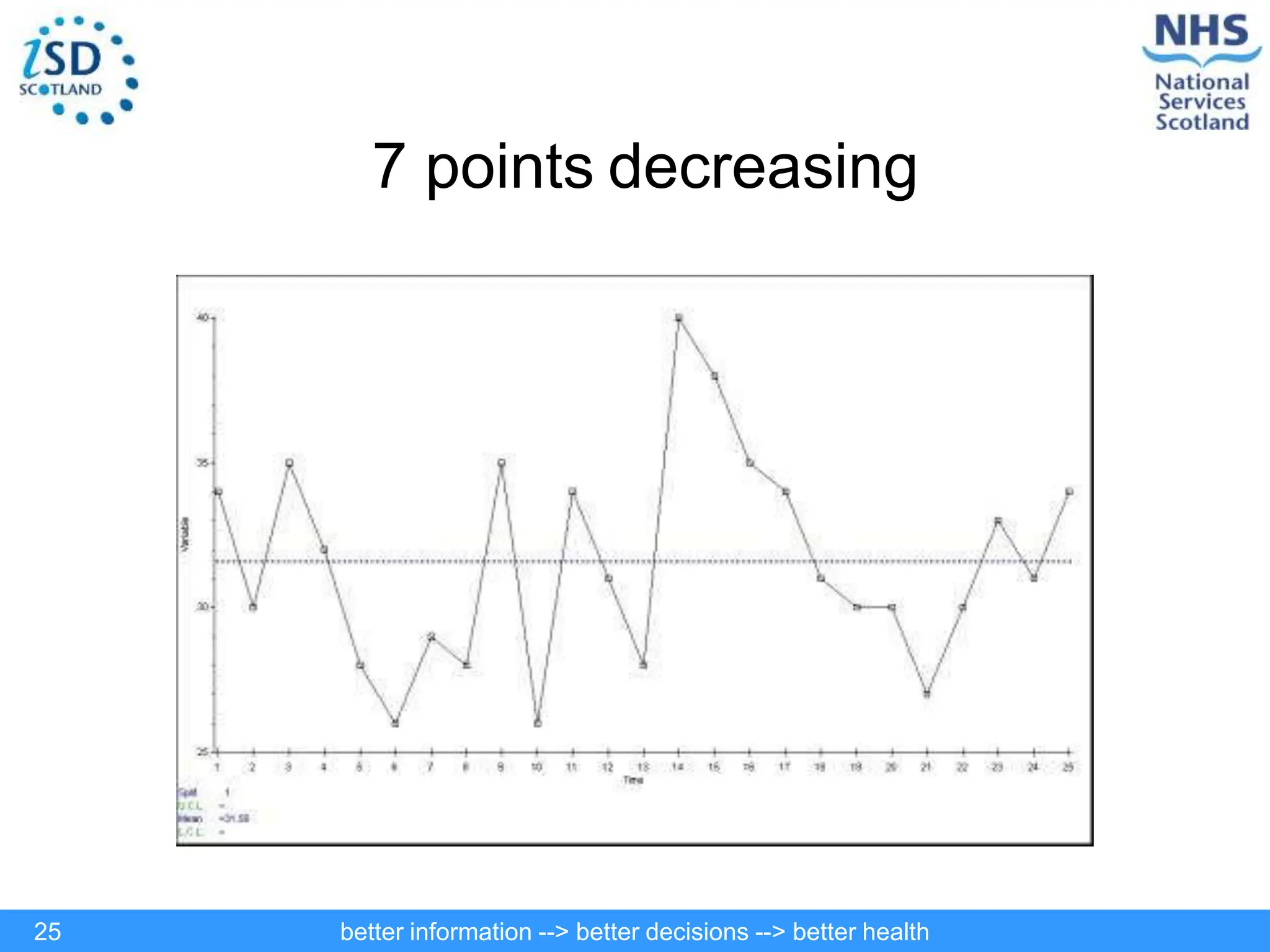
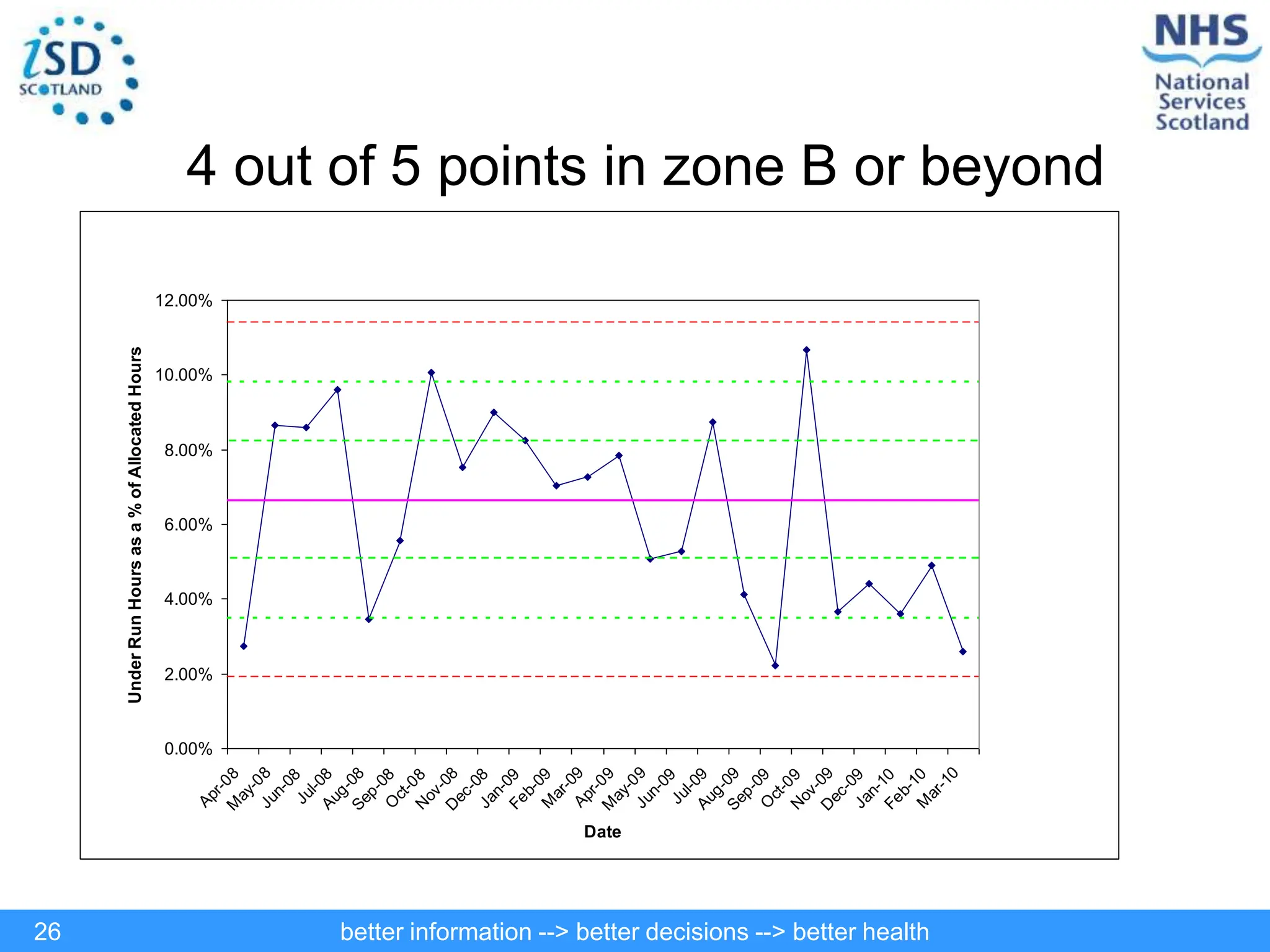
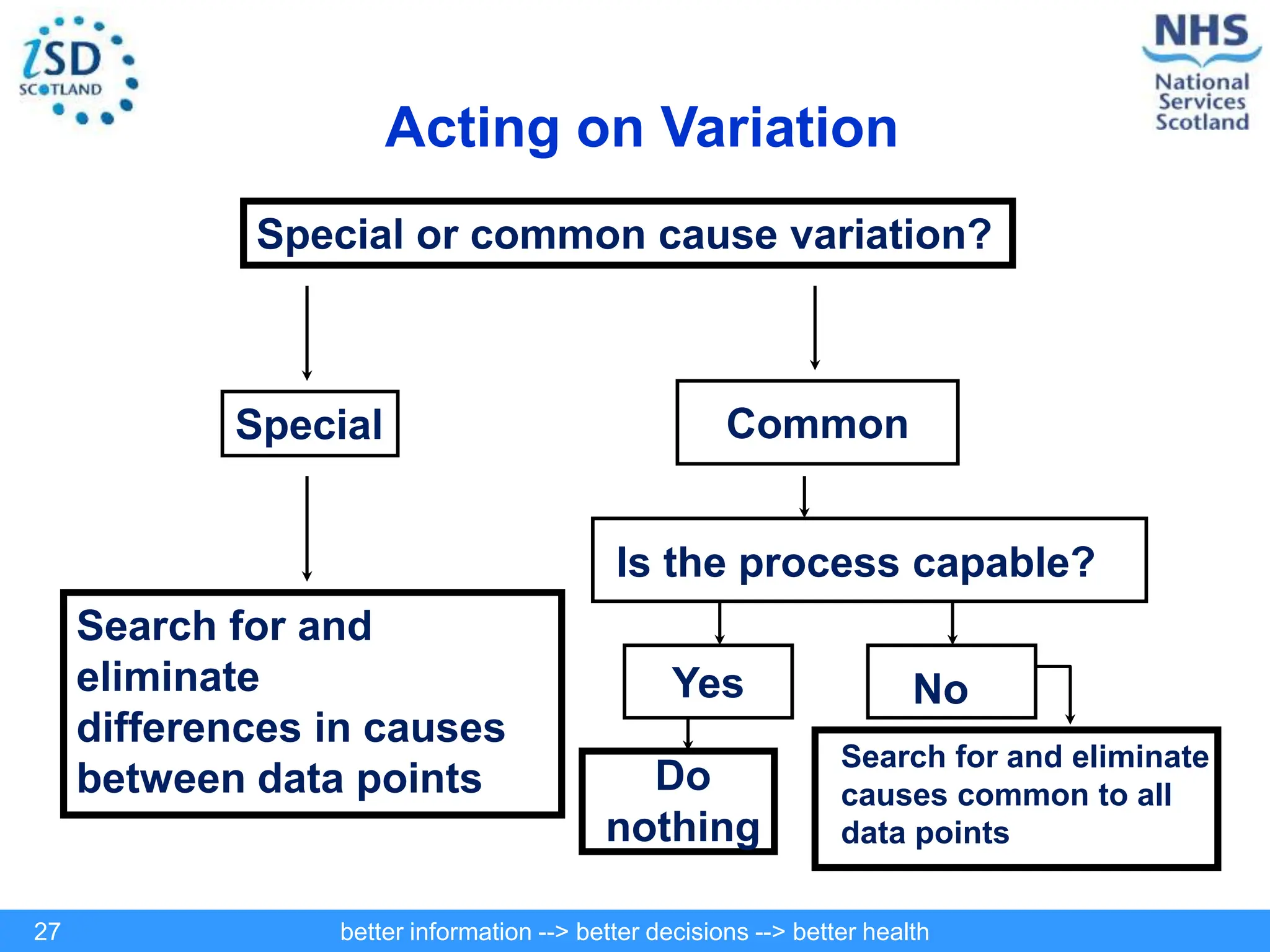
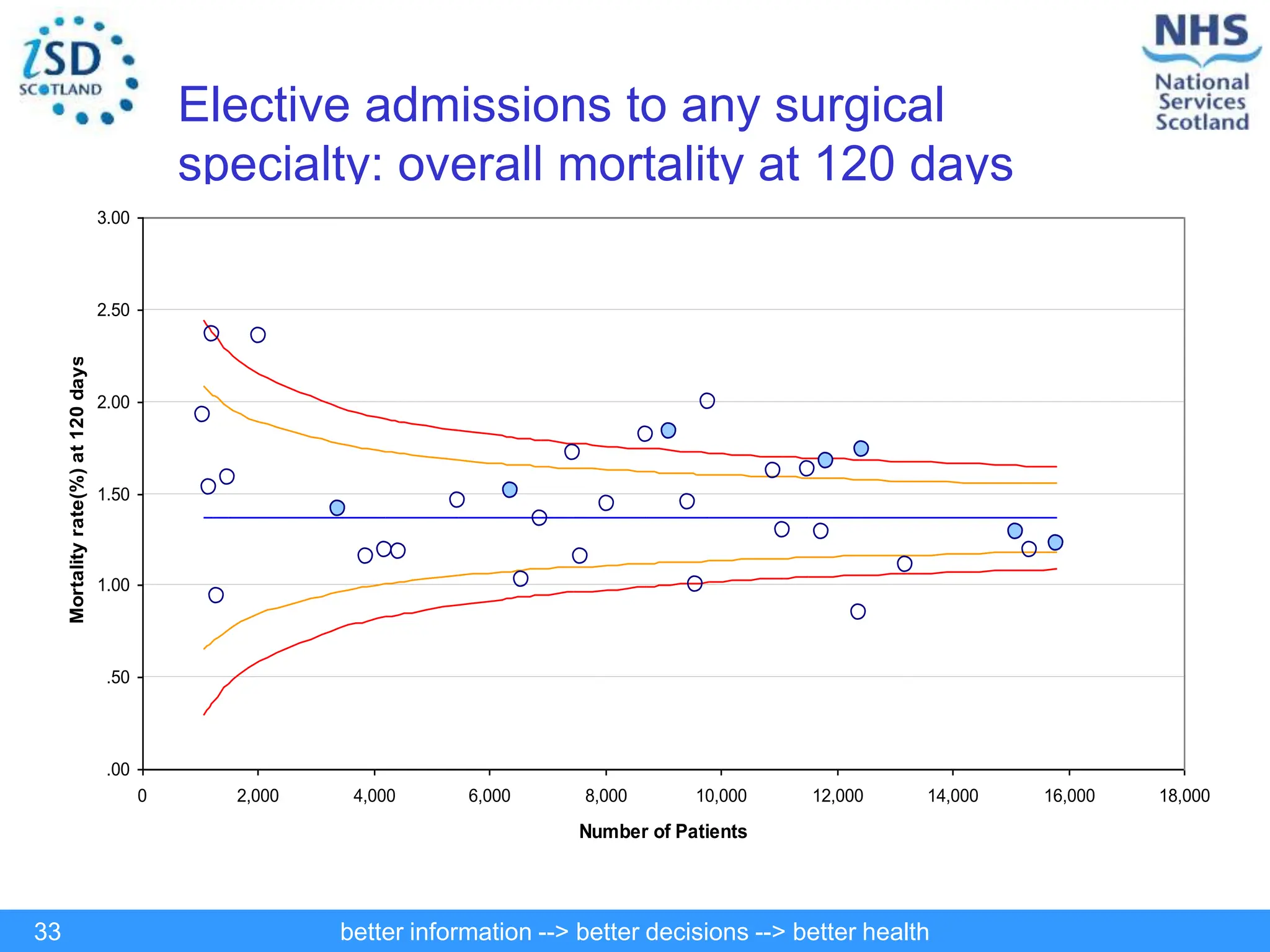
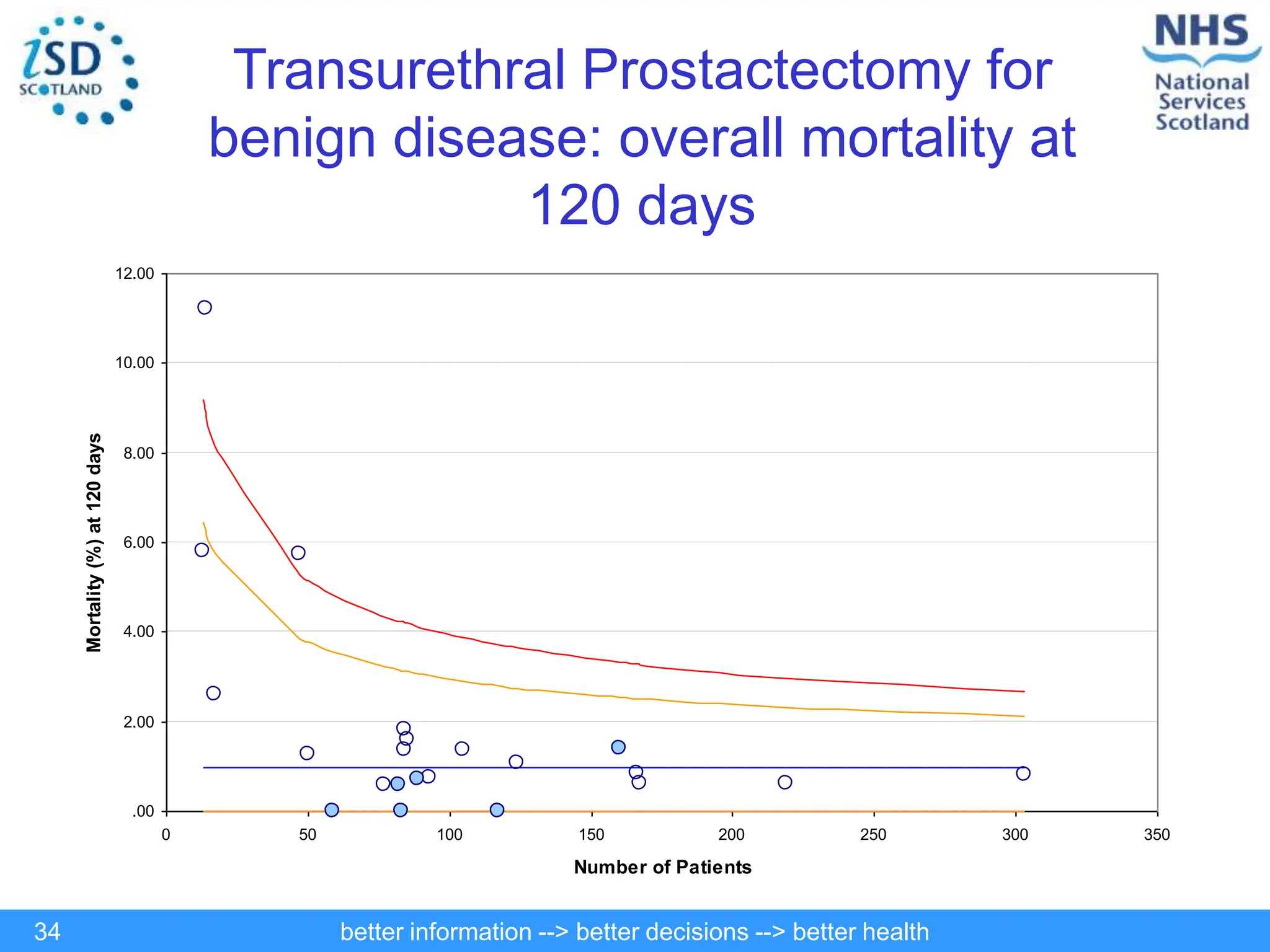
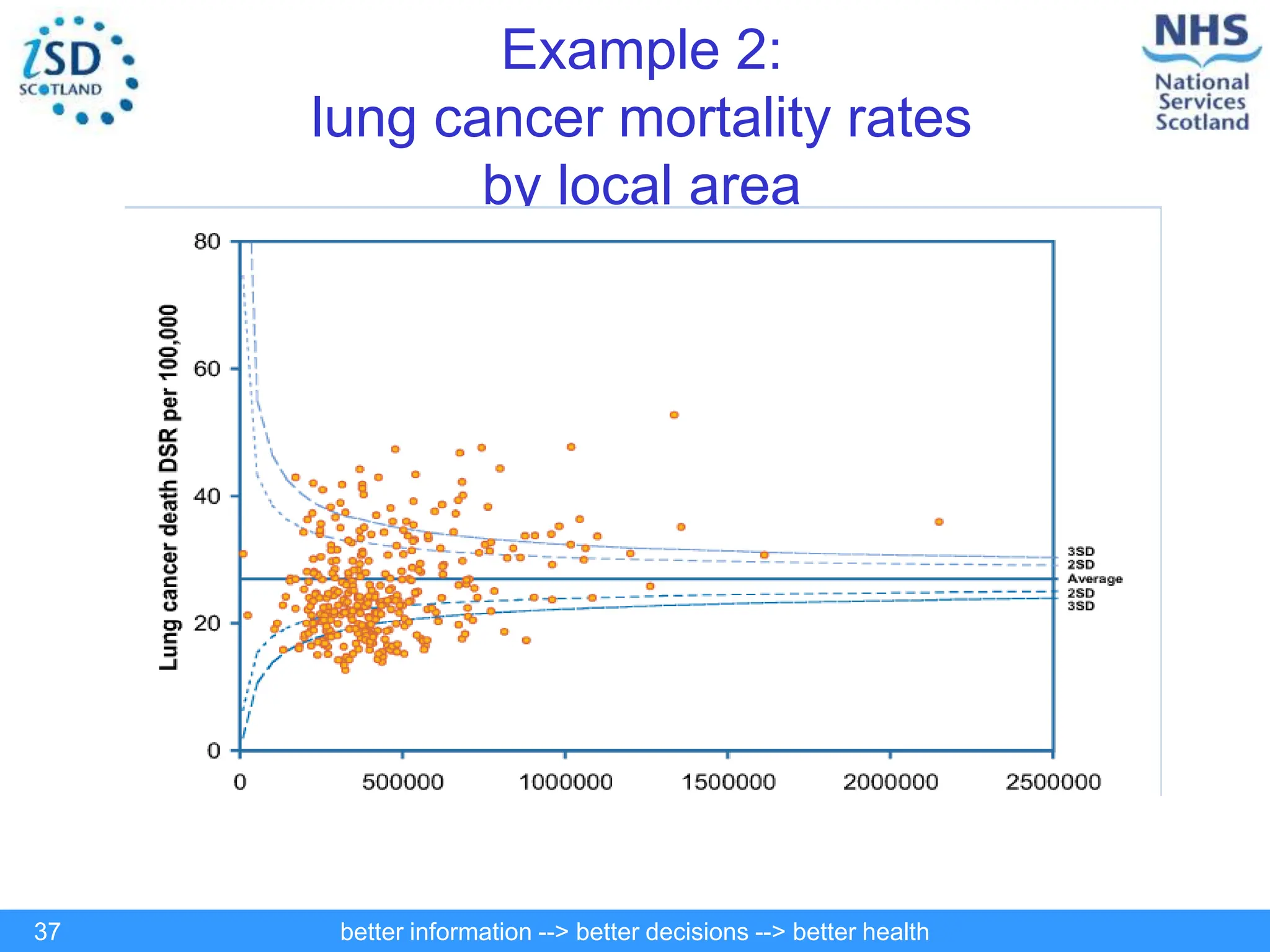
The document discusses statistical process control (SPC) and its application in public health to improve decision-making and health outcomes. It highlights the limitations of traditional ranking methods and presents SPC as a more effective approach to monitor and understand variations in health data using control charts. The use of control charts allows for better identification of performance issues, aiding in the management of health systems and the investigation of outliers.